专题训练十四 一次函数背景下的线段和差最值问题(共14张PPT)

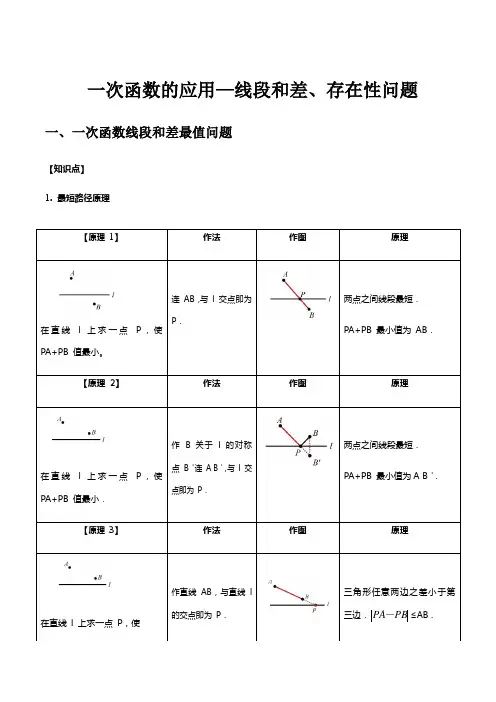
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P，使PA+PB 值最小。

连AB，与l 交点即为P．两点之间线段最短．PA+PB 最小值为AB．【原理2】作法作图原理在直线l 上求一点P，使PA+PB 值最小．作 B 关于l 的对称点B＇连A B＇，与l 交点即为P．两点之间线段最短．PA+PB 最小值为A B＇．【原理3】作法作图原理在直线l 上求一点P，使作直线AB，与直线l的交点即为P．三角形任意两边之差小于第三边．≤AB .PBPA－（1）求线段和最小时动点坐标或直线解析式； （2）求三角形周长最小值；（3）求线段差最大时点的坐标或直线解析式。

3. 口诀：“和小异，差大同”（一）一次函数线段和最小值问题【例题讲解】★★☆例题1．在平面直角坐标系xOy 中，y 轴上有一点P ，它到点(4,3)A ，(3,1)B 的距离之和最小，则点P 的坐标是( ) A ．(0,0)B ．4(0,)7C ．5(0,)7D ．4(0,)5【答案】C的值最大 .【原理 4】作法作图原理在直线 l 上求一点 P ，使的值最大 .作 B 关于 l 的对称点 B ＇作直线 A B ＇，与 l 交点即为 P ．三角形任意两边之差小于第三边．≤A B ＇ .PB PA －PB PA －PB PA －【解析】解：作A 关于y 轴的对称点C ，连接BC 交y 轴于P ，则此时AP PB +最小，即此时点P 到点A 和点B 的距离之和最小，(4,3)A ，(4,3)C ∴-，设直线CB 的解析式是y kx b =+，把C 、B 的坐标代入得：3413k bk b =-+⎧⎨-=+⎩，解得：47k =-，57b =，4577y x ∴=-+，把0x =代入得：57y =， 即P 的坐标是5(0,)7，故选：C ．【备注】本题考查了轴对称-最短路线问题，一次函数的解析式，坐标与图形性质等知识点，关键是能画出P 的位置，题目比较典型，是一道比较好的题目．★★☆练习1．如图，在平面直角坐标系中，已知点(2,3)A ，点(2,1)B -，在x 轴上存在点P 到A ，B 两点的距离之和最小，则P 点的坐标是 ．【答案】(1,0)-【解析】解：作A 关于x 轴的对称点C ，连接BC 交x 轴于P ，则此时AP BP +最小，A 点的坐标为(2,3)，B 点的坐标为(2,1)-，(2,3)C ∴-，设直线BC 的解析式是：y kx b =+，把B 、C 的坐标代入得：2123k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩．即直线BC 的解析式是1y x =--，当0y =时，10x --=，解得：1x =-，P ∴点的坐标是(1,0)-．故答案为：(1,0)-．【备注】本题考查了一次函数图象上点的坐标特征，用待定系数法求一次函数的解析式，轴对称-最短路线问题的应用，关键是能找出P 点，题目具有一定的代表性，难度适中．★★☆练习2．如图，直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，以线段AB 为边在第一象限内作正方形ABCD ．若点P 为x 轴上的一个动点，求当PC PD +的长最小时点P 的坐标．【答案】详见解析【解析】解：直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，则点A 、B 的坐标分别为：(0,3)，(4,0)，如图所示，过点C 作CH x ⊥轴交于点H ，90ABO BAO ∠+∠=︒，90ABO CBH ∠+∠=︒，CBH BAO ∴∠=∠，又90AOB CHB ∠=∠=︒，AB BC =，()AOB BHC AAS ∴∆≅∆，4CH OB ∴==，3HB OA ==，故点(7,4)C ，同理可得点(3,7)D ，确定点C 关于x 轴的对称点(7,4)C '-，连接C D '交x 轴于点P ，则此时PC PD +的长最小，将点C '、D 的坐标代入一次函数表达式并解得： 直线CD 的表达式为：116144y x =-+， 当0y =时，6111x =，故点61P，0)．(11【备注】本题考查的是一次函数上坐标点的特征，涉及到点的对称性、正方形性质等，本题的难点在于：通过证明三角形全等，确定点C、D的坐标．★★☆例题2．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，3OB=，D为边OB的中点，若E为x轴上的一个动点，当CDE∆的周长最小时，求点E OA=，4的坐标()A．(3,0)-B．(1,0)C．(0,0)D．(3,0)【答案】B【解析】解：如图，作点D关于x轴的对称点D'，连接CD'与x轴交于点E，连接DE．若在边OA上任取点E'与点E不重合，连接CE'、DE'、D E''由DE CE D E CE CD D E CE DE CE'+'=''+'>'='+=+，可知CDE∆的周长最小．OB=，D为边OB的中点，42∴=，OD∴，(0,2)D在矩形OACB 中，3OA =，4OB =，D 为OB 的中点，3BC ∴=，2D O DO '==，6D B '=，//OE BC ，Rt ∴△D OE Rt '∽△D BC '，∴OE D OBC D B '=' 即236OE = 1OE =，∴点E 的坐标为(1,0)故选：B ．【备注】此题主要考查轴对称--最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．★★☆练习1．如图，在平面直角坐标系中，点A 、B 的坐标分别为(1,4)和(3,0)，点C 是y 轴上的一个动点，连接AC 、BC ，当ABC ∆的周长最小值时，ABC ∆的面积为 ．【答案】3【解析】解：如图，作点A 关于y 轴的对称点A '，连接A B '交y 轴于点C '，此时ABC ∆'的周长最小，设直线A B ' 的解析式为y kx b =+，(1,4)A '-，(3,0)B ，∴430k b k b -+=⎧⎨+=⎩，1k ∴=-，3b =，∴直线A B ' 的解析式为3y x =-+，当0x =时，3y =，(0,3)C ∴'，ABC AA BAA C S SS∆'''∴=-11242122=⨯⨯-⨯⨯ 413=-=．所以ABC ∆'的面积为3．故答案为：3．【备注】本题考查了轴对称、最短路线问题、坐标与图形性质、三角形的面积，解决本题的关键是掌握轴对称的性质．★★☆练习2．如图，在平面直角坐标系中，直线122y x =+与x 轴、y 轴分别交于A 、B 两点，以AB 为边 在第二象限内作正方形ABCD ．（1）求点A 、B 的坐标，并求边AB 的长；（2）求点C 和点D 的坐标；（3）在x 轴上找一点M ，使MDB ∆的周长最小，请求出M 点的坐标，并直接写出MDB ∆的周长最小值．【答案】详见解析【解析】解： （1）对于直线122y x =+， 令0x =，得到2y =；令0y =，得到4x =-，(4,0)A ∴-，(0,2)B ，即4OA =，2OB =， 则224225AB =+=；（2）过D 作DE x ⊥轴，过C 作CF y ⊥轴，四边形ABCD 为正方形，AB BC AD ∴==，90ABC BAD BFC DEA AOB ∠=∠=∠=∠=∠=︒，90FBC ABO ∠+∠=︒，90ABO BAO ∠+∠=︒，90DAE BAO ∠+∠=︒，FBC OAB EDA ∴∠=∠=∠，()DEA AOB BFC AAS ∴∆≅∆≅∆，2AE OB CF ∴===，4DE OA FB ===，即426OE OA AE =+=+=，246OF OB BF =+=+=，则(6,4)D -，(2,6)C -；（3）如图所示，连接BD ，找出B 关于y 轴的对称点B '，连接DB '，交x 轴于点M ，此时BM MD DM MB DB +=+'='最小，即BDM ∆周长最小，(0,2)B ，(0,2)B ∴'-，设直线DB '解析式为y kx b =+，把(6,4)D -，(0,2)B '-代入得：642k b b -+=⎧⎨=-⎩，解得：1k =-，2b =-，∴直线DB '解析式为2y x =--，令0y =，得到2x =-，则M 坐标为(2,0)-， 此时MDB ∆的周长为21062+．【备注】本题属于一次函数综合题，涉及的知识有：待定系数法求一次函数解析式，坐标与图形性质，勾 股定理，全等三角形的判定与性质，正方形的性质，对称性质，以及一次函数与坐标轴的交点，熟练掌握 性质及定理是解本题的关键（二）一次函数线段差最大值问题【例题讲解】★★☆例题1．已知，如图点(1,1)A ，(2,3)B -，点P 为x 轴上一点，当||PA PB -最大时，点P的坐标为( )A ．1(,0)2B ．5(,0)4C ．1(,0)2-D ．(1,0)【答案】A【解析】解：作A 关于x 轴对称点C ，连接BC 并延长交x 轴于点P ， (1,1)A ，C ∴的坐标为(1,1)-，连接BC ，设直线BC 的解析式为：y kx b =+，∴123k b k b +=-⎧⎨+=-⎩， 解得：21k b =-⎧⎨=⎩， ∴直线BC 的解析式为：21y x =-+， 当0y =时，12x =， ∴点P 的坐标为：1(2，0)，当B ，C ，P 不共线时，根据三角形三边的关系可得：||||PA PB PC PB BC -=-<，∴此时||||PA PB PC PB BC -=-=取得最大值．故选：A ．【备注】此题考查了轴对称、待定系数法求一次函数的解析式以及点与一次函数的关系．此题难度较大，解题的关键是找到P 点，注意数形结合思想与方程思想的应用．★★☆练习1．平面直角坐标系中，已知(4,3)A 、(2,1)B ，x 轴上有一点P ，要使PA PB -最大，则P 点坐 标为【答案】(1,0)【解析】解：(4,3)A 、(2,1)B ，x 轴上有一点P ，||PA PB AB ∴-，∴当A ，B ，P 三点共线时，PA PB -最大值等于AB 长，此时，设直线AB 的解析式为y kx b =+，把(4,3)A 、(2,1)B 代入，可得3412k b k b =+⎧⎨=+⎩， 解得11k b =⎧⎨=-⎩， ∴直线AB 的解析式为1y x =-，令0y =，则1x =，P ∴点坐标为(1,0)，故答案为：(1,0)． 【备注】本题主要考查了坐标与图形性质，利用待定系数法求得直线AB 的解析式是解决问题的关键． ★★☆练习2．如图，在平面直角坐标系中，点A 的坐标为(0,4)，点B 的坐标为(6,0)，点P 在一次函数1322y x =+的图象上运动，则PB PA -的最大值为( )A ．2B ．233C ．4D ．143【答案】C【解析】解：如图，作点A 关于直线1322y x =+的对称点K ，连接AK 交直线于H ，连接PK ．AK PH ⊥，(0,4)A ，∴直线AK 的解析式为24y x =-+，由132224y x y x ⎧=+⎪⎨⎪=-+⎩，解得12x y =⎧⎨=⎩， (1H ∴，20，AH KH =，(2,0)K ∴．PB PA PB PK KB ∴-=-，∴当点P 在BK 的延长线上时，P B P K BK '-'=的值最大，最大值为624-=，故选：C ．【备注】本题考查一次函数图象上的点的特征、轴对称等知识，解题的关键是学会利用对称解决最值问题 属于中考常考题型．【题型知识点总结】一次函数最短路径问题注意事项：1. 根据“和小异，差大同”判断是否需要作对称；2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。

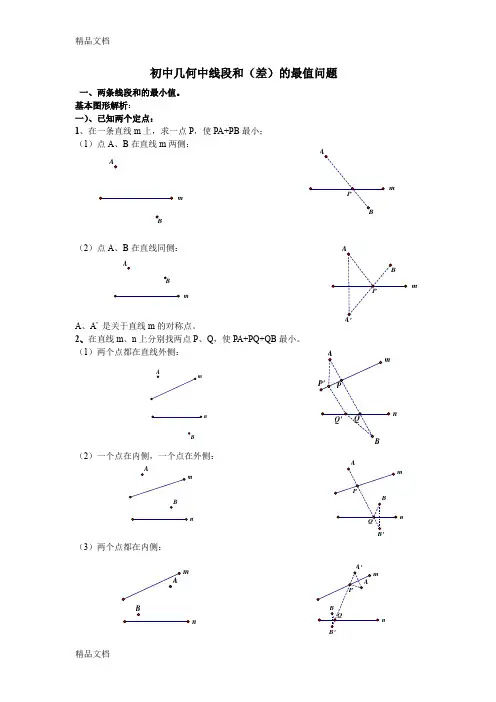
初中几何中线段和（差）的最值问题一、两条线段和的最小值。

基本图形解析： 一）、已知两个定点：1、在一条直线m 上，求一点P ，使PA+PB 最小； （1）点A 、B 在直线m 两侧：（2）点A 、B 在直线同侧：A 、A ’ 是关于直线m 的对称点。

2、在直线m 、n 上分别找两点P 、Q ，使PA+PQ+QB 最小。

（1）两个点都在直线外侧：（2）一个点在内侧，一个点在外侧：（3）两个点都在内侧：mmB mA Bmn mnn mnnnm（4）、台球两次碰壁模型变式一：已知点A 、B 位于直线m,n 的内侧，在直线n 、m 分别上求点D 、E 点，使得围成的四边形ADEB 周长最短.填空：最短周长=________________变式二：已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二）、一个动点，一个定点： （一）动点在直线上运动：点B 在直线n 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ）1、两点在直线两侧：2、两点在直线同侧：mnm nm nm（二）动点在圆上运动点B 在⊙O 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ） 1、点与圆在直线两侧：2、点与圆在直线同侧：三）、已知A 、B 是两个定点，P 、Q 是直线m 上的两个动点，P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点，使得PA+PQ+QB 的值最小。

(原理用平移知识解) （1）点A 、B 在直线m 两侧：过A 点作AC ∥m,且AC 长等于PQ 长，连接BC,交直线m 于Q,Q 向左平移PQ 长，即为P 点，此时P 、Q 即为所求的点。

（2）点A 、B 在直线m 同侧：mmmmQ Q练习题1．如图，∠AOB =45°，P 是∠AOB 内一点，PO =10，Q 、R 分别是OA 、OB 上的动点，求△PQR 周长的最小值为 ．2、 如图1，在锐角三角形ABC 中，AB=4,∠BAC=45°，∠BAC 的平分线交BC 于点D ，M,N 分别是AD 和AB 上的动点，则BM+MN 的最小值为 ． 3、如图，在锐角三角形ABC 中 ，AB=BAC=45，BAC 的平分线交BC 于D ，M 、N 分别是AD 和AB 上的动点，则BM+MN 的最小值是多少？4、如图4所示，等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点.若AE=2,EM+CM 的最小值为 .5、如图3，在直角梯形ABCD 中，∠ABC ＝90°，AD ∥BC ，AD ＝4，AB ＝5，BC ＝6，点P 是AB 上一个动点，当PC ＋PD 的和最小时，PB 的长为__________．6、 如图4，等腰梯形ABCD 中，AB=AD=CD=1，∠ABC=60°，P 是上底，下底中点EF 直线上的一点，则PA+PB 的最小值为 ．Q二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析：1、在一条直线m 上，求一点P ，使PA 与PB 的差最大； （1）点A 、B 在直线m 同侧：解析：延长AB 交直线m 于点P ，根据三角形两边之差小于第三边，P ’A —P ’B ＜AB ，而PA —PB=AB 此时最大，因此点P 为所求的点。

初中几何中线段和差的最大值与最小值练习题(最全)初中几何中线段和（差）的最值问题一、两条线段和的最小值基本图形解析：一）已知两个定点：1、在一条直线m上，求一点P，使PA+PB最小。

1）点A、B在直线m两侧：在直线m上找到点P使得PA=PB，则PA+PB最小。

2）点A、B在直线同侧：在直线m上找到点A'，使得A'是关于直线m的对称点，再找到点P使得PA'+PB最小，则PA+PB最小。

2、在直线m、n上分别找两点P、Q，使PA+PQ+QB最小。

1）两个点都在直线外侧：在直线m上找到点A'，使得A'是关于直线m的对称点，在直线n上找到点B'，使得B'是关于直线n的对称点，再找到点P和Q，使得PA'+PQ+QB'最小，则PA+PQ+QB最小。

2）一个点在内侧，一个点在外侧：在直线m上找到点P，使其与A点连线垂直直线m，再在直线n上找到点Q，使其与B点连线垂直直线n，使PA+PQ+QB最小。

3）两个点都在内侧：在直线m上找到点A'，使得A'是关于直线m的对称点，在直线n上找到点B'，使得B'是关于直线n的对称点，再找到点P和Q，使得PA'+PQ+QB'最小，则PA+PQ+QB最小。

4）、台球两次碰壁模型变式一：已知点A、B位于直线m,n的内侧，在直线n、m分别上求点D、E点，使得围成的四边形ADEB周长最短。

在直线m上找到点A'，使得A'是关于直线m的对称点，在直线n上找到点B'，使得B'是关于直线n的对称点，连接A'和B'，交直线m和n于D和E，使ADEB为矩形，则ADEB周长最短。

变式二：已知点A位于直线m,n的内侧,在直线m、n分别上求点P、Q点PA+PQ+QA周长最短。

在直线m上找到点A'，使得A'是关于直线m的对称点，连接AA'，在直线n上找到点Q，使得A'Q垂直直线n，连接AQ，使得PA+PQ+QA最小。

精心整理①当两点A和B在直线l同侧时，若求直线l上点P.使PA+PB最小值作点B关于直线l的对称点B’,连结AB’交直线l于点P,此时PA+PB=PA+PB’=AB’取除此之外的任意一点P’,根据三角形两边之和大于第三边，P’A+P’B=P’A+P’B’＞AB’,所以点P满足PA+PB最小值l（⋅＝OQ【分析】连接AB并延长交x轴于点P，作A点关于y轴的对称点A′连接A′B交y轴于点Q，求出点Q与y轴的交点坐标即可得出结论：连接AB并延长交x轴于点P，由三角形的三边关系可知，点P即为x轴上使得|PA－PB|的值最大的点。

∵点B是正方形ADPC的中点，∴P（3，0）即OP=3。

作A点关于y轴的对称点A′连接A′B交y轴于点Q，则A′B即为QA+QB的最小值。

∵A′（-1，2），B（2，1），设过A′B的直线为：y=kx+b，则2k b12k b=-+⎧⎨=+⎩，解得1k35b3⎧=-⎪⎪⎨⎪=⎪⎩。

∴Q（0，53），即OQ=53。

∴OP?OQ=3×53=5。

（2012四川攀枝花4分）如图，正方形ABCD中，AB=4，E是BC的中点，点P是对角线AC上一动点，则PE+PB同理，在Rt△AOC中，OA＝10，AC＝8，∴OC＝＝＝6。

∴CD＝8＋6＝14。

作点B关于MN的对称点B′，连接AB′，则AB′即为PA＋PB的最小值，B′D＝BD＝6，过点B′作AC的垂线，交AC的延长线于点E。

在Rt△AB′E中，∵AE＝AC＋CE＝8＋6＝14，B′E＝CD＝14，∴AB′＝＝＝14。

例6.（2012湖北十堰6分）阅读材料：P（x，0）是x可以看成点P与点A（0，1P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA＋PB的最小值．设点A关于x轴的对称点为A′，则PA=PA′，因此，求PA＋PB的最小值，只需求PA′＋PB的最小值，而点A′、B A′C=3，CB=3（1B的距（2（2）（1，如图所示：设点A关于x轴的对称点为A′，则PA=PA′，∴求PA＋PB的最小值，只需求PA′＋PB的最小值，而点A′、B间的直线段距离最短。

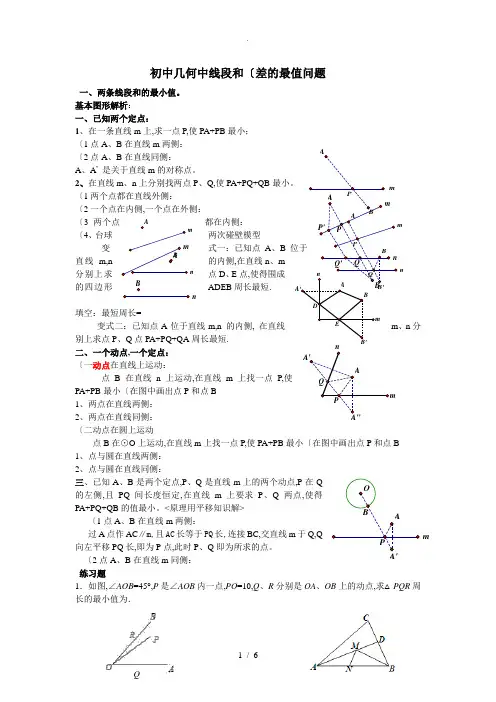
初中几何中线段和〔差的最值问题一、两条线段和的最小值。

基本图形解析：一、已知两个定点：1、在一条直线m 上,求一点P,使PA+PB 最小；〔1点A 、B 在直线m 两侧： 〔2点A 、B 在直线同侧：A 、A ’ 是关于直线m 的对称点。

2、在直线m 、n 上分别找两点P 、Q,使PA+PQ+QB 最小。

〔1两个点都在直线外侧： 〔2一个点在内侧,一个点在外侧： 〔3两个点都在内侧： 〔4、台球两次碰壁模型变式一：已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短. 填空：最短周长=________________ 变式二：已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. 二、一个动点,一个定点： 〔一动点在直线上运动： 点B 在直线n 上运动,在直线m 上找一点P,使PA+PB 最小〔在图中画出点P 和点B 1、两点在直线两侧：2、两点在直线同侧：〔二动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P,使PA+PB 最小〔在图中画出点P 和点B1、点与圆在直线两侧：2、点与圆在直线同侧：三、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。

<原理用平移知识解> 〔1点A 、B 在直线m 两侧：过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。

〔2点A 、B 在直线m 同侧：练习题1．如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为．P m A B Q P n m A B P'Q' n m A B Q P n m A B B' n m A B P m O A B A'E D m n A B A'B'P Qm n A A"A'2、如图1,在锐角三角形ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值为．3、如图,在锐角三角形ABC中,AB=52,∠BAC=45,BAC的平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少？4、如图4所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为.5、如图3,在直角梯形ABCD中,∠ABC＝90°,AD∥BC,AD＝4,AB＝5,BC＝6,点P是AB上一个动点,当PC＋PD的和最小时,PB的长为__________．6、如图4,等腰梯形ABCD中,AB=AD=CD=1,∠ABC=60°,P是上底,下底中点EF直线上的一点,则PA+PB的最小值为．7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为．8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm．10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点．则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为．13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为．14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为cm．〔结果不取近似值．15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则P A+PC的最小值是．16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN＝30°,B为AN弧的中点,P是直径MN上一动点,则PA＋PB的最小值为< ><A>2 <B><C>1 <D>2解答题1、如图9,正比例函数y=x的图象与反比例函数y=〔k≠0在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.〔1求反比例函数的解析式；〔2如果B为反比例函数在第一象限图象上的点〔点B与点A不重合,且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2〔x1＜x2是抛物线y=ax2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A〔3,6．〔1求此二次函数的解析式；〔2设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标；〔3在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标．3、如图10,在平面直角坐标系中,点A的坐标为〔1, ,△AOB的面积是.〔1求点B的坐标；〔2求过点A、O、B的抛物线的解析式；〔3在〔2中抛物线的对称轴上是否存在点C,使△AOC的周长最小？若存在,求出点C的坐标；若不存在,请说明理由；4．如图,抛物线y＝错误!x2－错误!x＋3和y轴的交点为A,M为OA的中点,若有一动点P,自M点处出发,沿直线运动到x轴上的某点〔设为点E,再沿直线运动到该抛物线对称轴上的某点〔设为点F,最后又沿直线运动到点A,求使点P运动的总路程最短的点E,点F的坐标,并求出这个最短路程的长．5．如图,已知在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x 轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D．将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F．〔1求经过A、B、C三点的抛物线的解析式；〔2当BE经过〔1中抛物线的顶点时,求CF的长；〔3在抛物线的对称轴上取两点P、Q〔点Q在点P的上方,且PQ＝1,要使四边形BCPQ的周长最小,求出P、Q两点的坐标．6．如图,已知平面直角坐标系,A,B两点的坐标分别为A<2,－3,B<4,－1若C<a,0>,D<a+3,0>是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短．7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.〔1若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标；〔2若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题<运用三角形两边之差小于第三边>基本图形解析：1、在一条直线m上,求一点P,使PA与PB的差最大；yCl x B A〔1点A 、B 在直线m 同侧：解析：延长AB 交直线m 于点P,根据三角形两边之差小于第三边,P ’A —P ’B ＜AB,而PA —PB=AB此时最大,因此点P 为所求的点。

【八年级压轴精选】一次函数背景下的存在性问题与最值问题，一题通关！自编一题，融合多种存在性问题和最值问题，若有兴趣补充编题的请留言，八下内容，解法要避开相似。

1、求解析式①用尺规作出直线BC和点D，②求直线BC的解析式，③求点D坐标；2、存在性问题(1)全等三角形存在性：①P为平面内一动点，且满足△ABC与△ABP全等，求点P坐标；②P为直线BC上一动点，Q为x轴上一动点，且满足△ABC与△CQP全等，求点P坐标(2)等腰三角形存在性：P为直线BC上一动点，△ABP为等腰三角形，求点P坐标；(3)直角三角形存在性：直线l过原点，且与BC平行，P为直线l上一动点，△ABP为直角三角形，求点P坐标；(4)等腰直角三角形存在性：P为第二象限内上一动点，△ABP为等腰直角三角形，求点P坐标；(5)等边三角形存在性（九年级用）P为第二象限内上一动点，△ABP为等边三角形，求点P坐标；(7)平行四边形存在性：①三定一动：P为平面内一动点，且以A、B、C、P为顶点的四边形为平行四边形，求点P坐标；②两定两动：P为直线AB上一动点，Q为y轴上一动点，且以B、C、P、Q为顶点的四边形为平行四边形，求点P、Q的坐标；(8)菱形存在性：P为直线BC上一动点，Q为平面内一动点，且以A、B、P、Q为顶点的四边形为菱形，求点P、Q的坐标；(9)矩形存在性：直线l过原点，且与BC平行，P为直线l上一动点，Q为平面内一动点，且以A、B、P、Q为顶点的四边形为矩形，求点P、Q的坐标；本讲先来解析部分小题：1、求解析式①用尺规作出直线BC和点D，②求直线BC的解析式，③求点D坐标；（考查内容：尺规作图、图形折叠、待定系数法求解析式，勾股定理或等积法求线段长）①折叠想到重合，全等，可得BC为∠ABO平分线，完成基本作图作已知角的角平分线即可，由D、O重合，可知BD=BO，CD=CO，CD⊥AB，所以在AB上截取BD=BO或CD=CO，或过C作CD⊥AB 于D(此法较繁)②待定系数法求直线解析式，需知两点，已知B（0，6）只要知道点C坐标，算OC长，八年级求线段长两种方法：勾股和等积，如下：再来解析2（7），考查平行四边形存在性，解法参考我之前文章：“平四”存在性问题探究2(7)平行四边形存在性：①三定一动：P为平面内一动点，且以A、B、C、P为顶点的四边形为平行四边形，求点P坐标；②两定两动：P为直线AB上一动点，Q为y轴上一动点，且以B、C、P、Q为顶点的四边形为平行四边形，求点P、Q的坐标；②码字太累，手写版本：上面方法优点：1、不会漏解，2、无需画图(5)等边三角形存在性（九年级用）P为第二象限内上一动点，△ABP为等边三角形，求点P坐标；解法参考我之前文章：一题5解。

2 m 2 专题十四 一次函数中的最值问题考点一 坐标系中两点之间的距离最值问题【方法点拨】①点到直线的垂线段最短；②两点之间线段最短。

1.如图，点 P 的坐标为（2，0），点 B 在直线 y ＝x +m 上运动，当线段 PB 最短时，PB 的长度是 2 + 2． 【思路点拨】当线段 PB 最短时，PB 与直线 y ＝x +m 垂直，根据解析式即可求得 C 、D 的坐标，然后根据勾股定理求得 CD ，然后根据三角形相似即可求得 PB 的最短长度．【解析】解：当线段 PB 最短时，PB ⊥CD ，如图所示：由直线 y ＝﹣x +m 可知，直线与坐标轴的交点为 C （﹣m ，0），D （0，m ），∴OC ＝m ，OD ＝m ，∴CD = 2m ，∵点 P 的坐标为（2，0），∴PC ＝2+m ，∵∠PCB ＝∠DCO ，∠PBC ＝∠DOC ＝90°，∴△PBC ∽△DOC ，PB ∴OD = PC PB ，即 = 2+n ， CD n ∴PB = 2 + 2 ． 2 m故答案为： 2 + 2m ． 【点睛】本题考查了垂线段最短的性质，一次函数图象上点的坐标特征，勾股定理的应用，三角形相似2n3 5 2 的判定和性质，熟知垂线段最短是解题的关键．2.如图，点 P 在第一象限，△ABP 是边长为 2 的等边三角形，当点 A 在 x 轴的正半轴上运动时，点 B 随之在 y 轴的正半轴上运动，运动过程中，点 P 到原点的最大距离是 1+ ；若将△ABP 的 PA 边长改为 2 2，另两边长度不变，则点 P 到原点的最大距离变为 1+ ．1【思路点拨】根据当 O 到 AB 的距离最大时，OP 的值最大，得到 O 到 AB 的最大值是2AB ＝1，此时在 斜边的中点 M 上，由勾股定理求出 PM ，即可求出答案；将△ABP 的 PA 边长改为 2 2，另两边长度不变，根据 22+22= (2 2)2，得到∠PBA ＝90°，由勾股定理求出 PM 即可【解析】解：取 AB 的中点 M ，连 OM ，PM ，在 Rt △ABO 中，OM = AB=1，在等边三角形 ABP 中，PM = 3，无论△ABP 如何运动，OM 和 PM 的大小不变，当 OM ，PM 在一直线上时，P 距 O 最远，1 ∵O 到 AB 的最大值是2 AB ＝1， 此时在斜边的中点 M 上，由勾股定理得：PM = 22 — 12 = 3，∴OP ＝1+ 3，将△AOP 的 PA 边长改为 2 2，另两边长度不变，∵22+22= (2 2)2，∴∠PBA ＝90°，由勾股定理得：PM = 12 + 22 = 5，∴此时 OP ＝OM +PM ＝1+5． 故答案为：1+ 3，1+ 5．【点睛】本题主要考查对直角三角形斜边上的中线性质，坐标与图形性质，三角形的三边关系，勾股定理的逆定理等边三角形的性质等知识点的理解和掌握，能根据理解题意求出 PO 的值是解此题的关键．2 ， 考点二 坐标内的线段和（差）最值问题【方法点拨】运用“将军饮马”模型和最小，差最大31. 如图，已知点 A 的坐标为（0，1），点 B 的坐标为（2，﹣2），点 P 在直线 y ＝﹣x 上运动，当|PA ﹣PB | 最大时点 P 的坐标为（）A ．（2，﹣2）B ．（4，﹣4）C ．（ 5 — 5）D ．（5，﹣5）2 【思路点拨】根据轴对称的性质及待定系数法可求得答案．【解析】解：作 A 关于直线 y ＝﹣x 对称点 C ，易得 C 的坐标为（﹣1，0）；连接 BC ，可得直线 BC 的方程为 y =— 4x — 4；5 5求 BC 与直线 y ＝﹣x 的交点，可得交点坐标为（4，﹣4）；此时|PA ﹣PB |＝|PC ﹣PB |＝BC 取得最大值，其他 BCP 不共线的情况，根据三角形三边的关系可得|PC ﹣PB |＜BC ；故选：B ．【点睛】本题考查轴对称的运用，有很强的综合性，难度较大．2. 如图，在平面直角坐标系中，Rt △OAB 的顶点 A 在 x 轴正半轴上，顶点 B 的坐标为（3， 3），点 C 的13 31 3+ 19 22 1坐标为（2，0）点 P 的斜边 OB 上一个动点，则 PC +PA 的最小值为（）A. 2 B ． 2 C ． 2 D ．2 7【思路点拨】作 A 关于 OB 的对称点 D ，连接 CD 交 OB 于 P ，连接 AP ，过 D 作 DN ⊥OA 于 N ，则此时PA +PC 的值最小，求出 AM ，求出 AD ，求出 DN 、CN ，根据勾股定理求出 CD ，即可得出答案．【解析】解：作 A 关于 OB 的对称点 D ，连接 CD 交 OB 于 P ，连接 AP ，过 D 作 DN ⊥OA 于 N ， 则此时 PA +PC 的值最小，∵DP ＝PA ，∴PA +PC ＝PD +PC ＝CD ，∵B （3， 3），∴AB = 3，OA ＝3，∵tan ∠AOB = AB = 3，OA 3∴∠AOB ＝30°，∴OB ＝2AB ＝2 3，由三角形面积公式得：1 ×OA ×AB = 1×OB ×AM ， 2 2∴AM = 3， ∴AD ＝2× 3 =3，∵∠AMB ＝90°，∠B ＝60°，∴∠BAM ＝30°，∵∠BAO ＝90°，∴∠OAM ＝60°，∵DN ⊥OA ，∴∠NDA ＝30°，31 2 3 ∴AN = 1AD = 3，由勾股定理得：DN =3 3， 22 21 ∵C （2，0）， ∴CN ＝3— 1 — 3=1， 2 2在 Rt △DNC 中，由勾股定理得：DC = 31 2 ，即 PA +PC 的最小值是．故选：B ．【点睛】本题考查了三角形的内角和定理，轴对称﹣最短路线问题，勾股定理，含 30 度角的直角三角形性质的应用，关键是求出 P 点的位置，题目比较好，难度适中．3. 如图所示的平面直角坐标系中，点 A 的坐标是（﹣4，4）、点 B 的坐标是（2，5），在 x 轴上有一动点 P ，要使 PA +PB 的距离最短，则点 P 的坐标是 ( — 4 ，O) ．【思路点拨】先作出点 A 关于 x 轴的对称点 A 1，再连接 A 1B ，求出直线 A 1B 的函数解析式，再把 y ＝0 代入即可得．【解析】解：作点 A 关于 x 轴的对称点 A 1（﹣4，﹣4），连接 A 1B 交 x 轴于 P ，12 + ( 323 )2 =∵B的坐标是（2，5），3．3∴直线A1B 的函数解析式为y＝1.5x+2，把P 点的坐标（n，0）代入解析式可得n=—4∴点P 的坐标是( —4 ，O)．【点睛】此题主要考查轴对称﹣﹣最短路线问题，综合运用了一次函数的知识．4.如图所示，四边形OABC 为正方形，边长为6，点A、C 分别在x 轴，y 轴的正半轴上，点D 在OA 上，且D点的坐标为（2，0），P是OB上的一个动点，试求PD+PA和的最小值是21O．【思路点拨】作出D关于OB的对称点D′，则D′的坐标是（0，2）．则PD+PA的最小值就是AD′的长，利用勾股定理即可求解．【解析】解：作出D关于OB的对称点D′，则D′的坐标是（0，2）．则PD+PA的最小值就是AD′的长．则OD′＝2，因而AD′=O Dะ2+O A2=4+36=21O．则PD+PA 和的最小值是21O．故答案是：2 1O．22【点睛】本题考查了正方形的性质，以及最短路线问题，正确作出 P 的位置是关键．5. 如图，一次函数 y = 1x +2 的图象分别与 x 轴、y 轴交于点 A 、B ，以线段 AB 为边在第二象限内作等腰 Rt △ABC ，∠BAC ＝90°．（ 可能 用到 的 公式 ： 若 A （ x 1 ， y 1 ）， Bx 2 ， y 2 ）， ①AB 中 点坐 标为 （x 1+x 2 ， y 1+y 2 ）； 2 2②AB = (x 1 — x 2)2 + (y 1 — y 2)2）（1） 求线段 AB 的长；（2） 过 B 、C 两点的直线对应的函数表达式．（3） 点 D 是 BC 中点，在直线 AB 上是否存在一点 P ，使得 PC +PD 有最小值？若存在，则求出此最小值；若不存在，则说明理由．【思路点拨】（1）求出一次函数图象与 x 轴交点坐标，再利用勾股定理求出 AB 的长即可；（2） 过 C 作 CE 垂直于 x 轴，可得出三角形 ACE 与三角形 AOB 全等，进而确定出 C 坐标，利用待定系数法求出直线 BC 解析式即可；（3） 根据中点坐标公式，可得 D 点坐标，根据轴对称的性质，可得 D ′点，两点之间线段最短，可得 P点，根据解方程组，可得 E 点坐标，根据中点坐标公式，可得 D ′，根据两点间的距离，可得答案．【解析】解：（1）对于一次函数 y = 1x +2，令 x ＝0，得到 y ＝2，令 y ＝0，得到 x ＝﹣4，即 A （﹣4，0），B （0，2），∴OA ＝4，OB ＝2，则 AB = OA 2 + OB 2 =2 5；（2）过 C 作 CE ⊥x 轴，可得∠ECA +∠CAE ＝90°，3 3 ∵△BAC 为等腰直角三角形，∴AC ＝AB ，且∠BAC ＝90°，∴∠CAE +∠OAB ＝90°，∴∠ECA ＝∠OAB ，在△ECA 和△OAB 中，²ECA = ²OAB ²CEA = ²AOB = 9O° CA = AB∴△ACE ≌△BAO （AAS ），∴CE ＝OA ＝4，AE ＝OB ＝2，即 OE ＝OA +AE ＝6，∴点 C 的坐标为（﹣6，4）．设直线 BC 解析式为 y ＝kx +b ，把 B （0，2）与 C （﹣6，4）代入得： b = 2 ， — 6k + b = 4解得： k =— 1，b = 2 则直线 BC 解析式为 y =— 1x +2；（3） ，作出 D 关于直线 AB 的对称点 D ′，连接 CD ′，交直线 AB 于点 P ，此时 CP +DP 最小，∵点 D 为 BC 的中点，O —6 2+4∴点 D 的坐标为（ 2 ，2 ），即 D （﹣3，3）， ∵直线 AB 解析式为 y = 1x +2，k = 1，2 2∴直线 DD ′的 k ＝﹣2，设直线 DD ′的解析式为 y ＝kx +b ，将 k ＝﹣2，D （﹣3，3）代入，解得 b ＝﹣3，∴直线 DD ′解析式为 y ＝﹣2x ﹣3，( — 6 + 1)2 + (4 + 1)2 2与直线 AB 解析式联立得： 解得： x =— 2， y = 1y =— 2x — 3 y = 1 x + 2 ，即两直线交点 E 坐标为（﹣2，1）．设D ′（x ，y ），由中点坐标公式，得x —3y+3 2=—2， 2 =1， 解得 x ＝﹣1，y ＝﹣1，∴D ′（﹣1，﹣1），则最小值为 CD ′==5 2．【点睛】本题考查了一次函数综合题，解（1）的关键是利用两点间的距离公式；解（2）的关键是利用全等三角形的判定与性质得出 C 点坐标，又利用了待定系数法求函数解析式；解（3）的关键是利用轴对称的性质得出 P 点坐标，又利用了对称点的中点在对称轴上得出 D ′点坐标．6. 在平面直角坐标系上，已知点 A （8，4），AB ⊥y 轴于 B ，AC ⊥x 轴于 C ，直线 y ＝x 交 AB 于 D ．（1） 直接写出 B 、C 、D 三点坐标；（2） 若 E 为 OD 延长线上一动点，记点 E 横坐标为 a ，△BCE 的面积为 S ，求 S 与 a 的关系式；（3） 当 S ＝20 时，过点 E 作 EF ⊥AB 于 F ，G 、H 分别为 AC 、CB 上动点，求 FG +GH 的最小值．【思路点拨】（1）首先证明四边形 ABOC 是矩形，再根据直线 y ＝x 是第一象限的角平分线，可得 OB ＝BD ，延长即可解决问题；（2） 根据 S ＝S △OBE +S △OEC ﹣S △OBC 计算即可解决问题；（3） 首先确定点 E 坐标，如图二中，作点 F 关于直线 AC 的对称点 F ′，作 F ′H ⊥BC 于 H ，交 AC 于G ．此时 FG +GH 的值最小；【解析】解：（1）∵AB ⊥y 轴于 B ，AC ⊥x 轴于 C ，∴∠ABO＝∠ACO＝∠COB＝90°，∴四边形ABOC 是矩形，∵A（8，4），∴AB＝OC＝8，AC＝OB＝4，∴B（0，4），C（8，0），∵直线y＝x 交AB 于D，∴∠BOD＝45°，∴OB＝DB＝4，∴D（4，4）．（2）由题意E（a，a），1 ×4×a+ 1 ×8×a—1 ×4×8＝6a﹣16．∴S＝S OBE+S OEC﹣S OBC=△△△ 2 2 2（3）当S＝20 时，20＝6a﹣16，解得a＝6，∴E（6，6），∵EF⊥AB 于F，∴F（6，4），如图二中，作点F 关于直线AC 的对称点F′，作F′H⊥BC 于H，交AC 于G．此时FG+GH 的值最小．∵∠ABC＝∠F′BH，∠BAC＝∠F′HB，∴△ABC∽△HBF′，AC BC∴=，4 51O ∵AC ＝4，BC = 42 + 82 =4 5，BF ′＝AB +AF ′＝8+2＝10，4∴F ะะ = ，∴F ′H ＝2 5，∴FG +GH 的最小值＝F ′H ＝2 5．【点睛】本题考查一次函数综合题、矩形的判定和性质、三角形的面积、相似三角形的判定和性质、轴对称最短问题等知识，解题的关键是学会利用分割法求三角形的面积，学会利用轴对称解决最短问题， 属于中考压轴题．考点三 坐标系中三角形周长最小问题【方法点拨】通常已知一线段是定值，运用“将军饮马”模型求另外两线段和最小1. 如图，在直角坐标系中，点 A 、B 的坐标分别为（1，4）和（3，0），点 C 是 y 轴上的一个动点，且 A 、B 、C 三点不在同一条直线上，当△ABC 的周长最小时，点 C 的坐标是 （0，3） ．【思路点拨】根据轴对称做最短路线得出 AE ＝B ′E ，进而得出 B ′O ＝C ′O ，即可得出△ABC 的周长最小时 C 点坐标．【解析】解：作 B 点关于 y 轴对称点 B ′点，连接 AB ′，交 y 轴于点 C ′，此时△ABC 的周长最小，∵点 A 、B 的坐标分别为（1，4）和（3，0），∴B ′点坐标为：（﹣3，0），AE ＝4，则 B ′E ＝4，即 B ′E ＝AE ，∵C ′O ∥AE ，∴B ′O ＝C ′O ＝3，∴点 C ′的坐标是（0，3），此时△ABC 的周长最小．故答案为（0，3）．【点睛】此题主要考查了利用轴对称求最短路线以及平行线的性质，根据已知得出C 点位置是解题关键．2.在平面直角坐标系中，矩形OACB 的顶点O 在坐标原点，顶点A、B 分别在x 轴y 轴的正半轴上，OA＝3，OB＝4，D 为OB 的中点，点E 为边OA 上的一个动点．（1）求线段CD 所在直线的解析式；（2）当△CDE 的周长最小时，求此时点E 的坐标；（3）当点E 为OA 中点时，坐标平面内，是否存在点F，使以D、E、C、F 为顶点的四边形是平行四边形？若存在，请直接写出F 点的坐标；若不存在，请说明理由．【思路点拨】（1）先求出C、D 的坐标，再用待定系数法即可求出线段CD 所在直线的解析式；（2）当△CDE 的周长最小时，DE+CE 最小；作点D 关于OA 的对称点D′，连接CD′交OA 于E，DE+CE 最小，证明△OED′∽△AEC，得出比例式求出OE 即可；（3）分三种情况：①CE 为对角线时，作FM⊥x 轴于M；证明△EMF≌△CBD，得出OM＝BC＝3，FM ＝DB＝2，OM＝1.5+3＝4.5，即可得出F 的坐标；②DE 为对角线时，作FN⊥x 轴于N，则F1N∥FM，根据平行线分线段成比例定理得出NE＝ME＝3，NF1＝FM＝2，ON＝1.5，即可得出结果；③DC 为对角线时，作F1Q⊥y 轴于Q，作F2P⊥y 轴于P；同②，即可得出结果．【解析】解：（1）∵四边形OACB是矩形，∴AC＝OB＝4，∠OBC＝90°，332∵D 为 OB 的中点，∴OD ＝BD ＝2，∴C （3，4），D （0，2），设线段 CD 所在直线的解析式为 y ＝kx +b ，代入 C （3，0），D （0，2）得： 3k + b = 4， b = 2解得：k = 2，b ＝2， ∴线段 CD 所在直线的解析式为：y = 2x +2； （2） 当△CDE 的周长最小时，DE +CE 最小；作点 D 关于 OA 的对称点 D ′，连接 CD ′交 OA 于 E ，如图 1 所示：则 D ′（0，﹣2），DE ＝DE ′，∴DE +CE ＝D ′E +CE ═CD ′，∵∠OBC ＝90°，BD ′＝6，∵AC ∥OB ，∴△OED ′∽△AEC ，O EO D ะ2 1 ∴AE = AC = 4 = ， ∴AE ＝2AE ，∵OA ＝3，∴OE ＝1，∴E （1，0）；（3） 存在；分三种情况：①CE 为对角线时，作 FM ⊥x 轴于 M ；如图 2 所示：∵BC ∥OA ，∴∠MEC ＝∠BCE ，∵四边形 DEFC 是平行四边形，∴CD ∥EF ，∴∠FEC ＝∠DCE ，∴∠MEF ＝∠BCD ，在△EMF 和△CBD 中，²FะE = ²DBC = 9O°²ะEF = ²BCD ，EF = CD∴△EMF≌△CBD（AAS），∴OM＝BC＝3，FM＝DB＝2，∴OM＝1.5+3＝4.5，∴F（4.5，2）；②DE 为对角线时，作F1N⊥x 轴于N，则F1N∥FM，如图2 所示：∵EF1＝CD＝EF1，∴NE＝ME＝3，NF1＝FM＝2，∴ON＝1.5，∴F1（﹣1.5，﹣2）；③DC 为对角线时，作F1Q⊥y 轴于Q，作F2P⊥y 轴于P，如图所示：同②得：PF2＝F1Q＝ON＝，1.5，PD＝DQ＝4，∴OP＝6，∴F2（1.5，6）；综上所述：F点的坐标为（4.5，2），或（1.5，6），或（﹣1.5，2）．【点睛】本题是一次函数综合题，考查了矩形的性质、用待定系数法确定一次函数的解析式、相似三角形的判定与性质等知识；本题难度较大，综合性强，特别是（2）、（3）中，需要证明三角形相似或三角形全等才能得出结果．3.如图，在平面直角坐标系中，矩形OACB 的顶点O 在坐标原点，顶点A、B 分别在x 轴、y 轴的正半轴上，OA＝3，OB＝4，D 为边OB 的中点．（1）点D 的坐标为（0，2）；（2）若E 为边OA 上的一个动点，当△CDE 的周长最小时，求点E 的坐标．【思路点拨】由于C、D 是定点，则CD 是定值，如果△CDE 的周长最小，即DE+CE 有最小值．为此，作点D 关于x 轴的对称点D′，当点E 在线段CD′上时，△CDE 的周长最小．【解析】解：（1）∵OB＝4，D为边OB的中点，∴OD＝2，∴D（0，2），故答案为：（0，2）；（2）如图，作点D 关于x 轴的对称点D′，连接CD′与x 轴交于点E，连接DE．若在边OA 上任取点E′与点E 不重合，连接CE′、DE′、D′E′由DE′+CE′＝D′E′+CE′＞CD′＝D′E+CE＝DE+CE，可知△CDE 的周长最小．∵在矩形 OACB 中，OA ＝3，OB ＝4，D 为 OB 的中点，∴BC ＝3，D ′O ＝DO ＝2，D ′B ＝6，∵OE ∥BC ， O E D ะO ∴Rt △D ′OE ∽Rt △D ′BC ，有B C = D ะB ，∴OE ＝1，∴点 E 的坐标为（1，0）．【点睛】此题主要考查轴对称﹣﹣最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．考点四 坐标系中四边形周长最小问题【方法点拨】已知两线段为定值，通过平移的方法，运用“将军饮马”模型求另外两线段和最小 71. 如图，当四边形 PABN 的周长最小时，a 的值为 ． 4【思路点拨】作 B 关于 x 轴的对称点 C ，连结 CN ，作平行四边形 PNCD ，因为 AB 、PN 为定值 所以 PA +BN 最小即可 因为 BN ＝CN ＝PD 所以只要 AP +PD 最小 作直线 AD 交 x 轴于 Q ，当 P 与 Q 重合时，AP +PD ＝AD 最小．【解析】解：作 B 关于 x 轴的对称点 C ，连结 CN ，作平行四边形 PNCD ，44∵AB 、PN 为定值∴PA +BN 最小即可∵BN ＝CN ＝PD∴只要 AP +PD 最小作直线 AD 交 x 轴于 Q ，当 P 与 Q 重合时，AP +PD ＝AD 最小∵A （1，3）、D （2，﹣1）∴直线 AD 为：y ＝﹣4x +7 当 y ＝0 时，x = 7， 7 ∴Q 为（4，0） ∵P 、Q 重合∴a = 7． 【点睛】本题考查轴对称﹣最短问题，平行四边形的性质、一次函数的应用等知识，解题的关键是学会构建平行四边形，利用对称解决最短问题，属于中考常考题型．2. 在平面直角坐标系中，矩形 OACB 的顶点 O 在坐标原点，顶点 A 、B 分别在 x 轴、y 轴的正半轴上，OA ＝3，OB ＝4，D 为边 OB 的中点．若 E 、F 为边 OA 上的两个动点，且 EF ＝2，当四边形 CDEF 的周长 1 最小时，求点 E 、F 的坐标分别为 （ 3 7 ，0），（ 3，0） ，并在图中画出示意图．【思路点拨】由于 DC 、EF 的长为定值，如果四边形 CDEF 的周长最小，即 DE +FC 有最小值．为此， 作点 D 关于 x 轴的对称点 D '，在 CB 边上截取 CG ＝2，当点 E 在线段 D ′G 上时，四边形 CDEF 的周长最小．【解析】解：如图，作点 D 关于 x 轴的对称点 D '，在 CB 边上截取 CG ＝2，连接 D 'G 与 x 轴交于点 E ， 在 EA 上截取 EF ＝2，∵GC ∥EF ，GC ＝EF ，∴四边形 GEFC 为平行四边形，有 GE ＝CF ． 又∵DC 、EF 的长为定值，∴此时得到的点 E 、F 使四边形 CDEF 的周长最小，∵OE ∥BC ， O E D ะO ∴Rt △D 'OE ∽Rt △D 'BG ，有B G = D ะB ．∴OE = D ะO ·B G = D ะO ·(B C —C G ) = 2×1 = 1 D ะB D ะB 6 3 ∴OF ＝OE +EF = 1 +2= 7．3 317 ∴点 E 的坐标为（ 3 1，0），点 F 的坐标为（ 3 7 ，0）．故答案为：（3，0），（3，0）．【点睛】此题主要考查轴对称﹣﹣最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．考点五 其它最值问题【方法点拨】根据具体题型求最值 1．若一次函数 y ＝kx +b ，当﹣2≤x ≤6 时，函数值的范围为﹣11≤y ≤9， 则此一次函数的解析式为 y = 5 x — 6 或 y =— 5 x + 4 ．2 2【思路点拨】根据函数自变量的取值范围用待定系数法求函数解析式．【解析】解：∵y 是 x 的一次函数，当﹣2≤x ≤6 时，﹣11≤y ≤9．2 2 2 2 设所求的解析式为 y ＝kx +b ，分两种情况考虑：（1）将 x ＝﹣2，y ＝﹣11 代入得：﹣11＝﹣2k +b ，将 x ＝6，y ＝9 代入得：9＝6k +b ，联立解得：k = 5，b ＝﹣6，则函数的解析式是 y = 5x ﹣6；（2）将 x ＝6，y ＝﹣11 代入得：﹣11＝6k +b ，将 x ＝﹣2，y ＝9 代入得：9＝﹣2k +b ，联立解得：k =— 5，b ＝4，则函数的解析式是 y =— 5x +4． 综上，函数的解析式是 y = 5x ﹣6 或 y =— 5x +4． 2 2 故答案为：y = 5x ﹣6 或 y =— 5x +4 2 2【点睛】本题要注意利用一次函数自变量的取值范围，来列出方程组，求出未知数，写出解析式．2. 如图，在平面直角坐标系中，已知点 M （2，﹣3）、N （6，﹣3），连接 MN ，如果点 P 在直线 y ＝﹣x +1上，且点 P 到直线 MN 的距离不小于 1，那么称点 P 是线段 MN 的“疏远点”．（1） 判断点 A （2，﹣1）是否是线段 MN 的“疏远点”，并说明理由；（2） 若点 P （a ，b ）是线段 MN 的“疏远点”，求 a 的取值范围；（3） 在（2）的前提下，用含 a 的代数式表示△MNP 的面积 S △MNP ，并求 S △MNP 的最小值．【思路点拨】（1）求出 A 到 MN 的距离，再判断即可；（2） 根据“疏远点”的意义求出 b 的范围，再代入求出 a 的范围即可；（3） 根据“疏远点”的意义得出 S MNP = 1 ×4×|﹣a +1﹣（﹣3）|，再去掉绝对值符号即可． △ 2【解析】解：（1）点A（2，﹣1）是线段MN的“疏远点”，并说明理由理由是：∵M（2，﹣3）、N（6，﹣3），A（2，﹣1），∴A 到直线MN 的距离为﹣1﹣（﹣3）＝2＞1，∵点P到直线MN的距离不小于1，那么称点P是线段MN的“疏远点”，∴点A（2，﹣1）是线段MN的“疏远点”；（2）∵点P（a，b）是线段MN的“疏远点”，M（2，﹣3）、N（6，﹣3），∴|b﹣（﹣3）|≥1，∴b≥﹣2 或b≤﹣4，代入y＝﹣x+1 得：﹣a+1≥﹣2 或﹣a+1≤﹣4，解得：a≤3 或a≥5，即 a 的取值范围是a≤3 或a≥5；（3）∵M（2，﹣3）、N（6，﹣3），∴MN＝6﹣2＝4，∴S =1 ×4×|﹣a+1﹣（﹣3）|= — 2a + 8(a＜4)△MNP 2，2a — 8(a＞4)∵a≤3 或a≥5，∴S△MNP的最小值是2．【点睛】本题考查了一次函数图象上点的特征，一次函数的性质等知识点，能根据“疏远点”的意义列出算式是解此题的关键．3.对某一个函数给出如下定义：若存在实数M＞0，对于任意的函数值y，都满足﹣M≤y≤M，则称这个函数是有界函数，在所有满足条件的M 中，其最小值称为这个函数的边界值．例如，图中的函数是有界函数，其边界值是1．（1）函数y＝x+1（﹣4≤x≤2）是不是有界函数？若是有界函数，求其边界值；（2）若函数y＝﹣x+1（a≤x≤b，b＞a）的边界值是2，且这个函数的最大值也是2，求b 的取值范围．(x — O)2 + (O — 1)2【思路点拨】（1）根据有界函数的定义即可得出函数 y ＝x +1（﹣4≤x ≤2）是有界函数，再代入 x ＝﹣4和 x ＝2 即可得出其边界值；（2）根据一次函数的性质可得出函数 y ＝﹣x +1 是单减函数，结合函数的最大值为 2 即可得出 a 的值， 再代入 b 的值结合有界函数的定义以及该函数的边界值即可得出关于 b 的一元一次不等式组，解不等式组即可得出 b 的取值范围；【解析】解：（1）根据有界函数的定义知，函数 y ＝x +1（﹣4≤x ≤2）是有界函数．∵﹣4+1＝﹣3，2+1＝3，∴y ＝x +1（﹣4＜x ≤2）边界值为 3．（2）∵k ＝﹣1＜0，∴函数 y ＝﹣x +1 的图象是 y 随 x 的增大而减小，∴当 x ＝a 时，y ＝﹣a +1＝2，解得：a ＝﹣1；当 x ＝b 时，y ＝﹣b +1，— 2 ≤— b + 1 ≤ 2∴ b ＞a ，a =— 1∴﹣1＜b ≤3；【点睛】本题考查了一次函数的性质、有界函数的定义以及解一元一次不等式组，解题的关键是：（1）根据有界函数的定义判断一个函数是否为有界函数；（2）找出关于 b 的一元一次不等式组．4. 请阅读下述材料，并解答问题例：说明代数式 x 2 + 1 + (x — 3)2 + 4的几何意义，并求它的最小值．解： 在平面直角坐标系中， 已知两点 P 1 （ x 1 ， y 1 ）， P 2 （ x 2 ， y 2 ） 则这两点间的距离公式为：P 1P 2=所以原式= +如图建立直角坐标系，点 P （x ，0）是 x 轴上一点，则 (x — O)2 + (O — 1)2可以看成点 P 与点 A （0，1） (x 1 — x 2)2 + (y 1 — y 2)2(x — 3)2 + (O — 2)2(x — 1)2 + 1 的距离， (x — 3)2 + (O — 2)2可以看成点 P 与点 B （3，2）的距离，所以原代数式的值可以看成线段 PA 与 PB 的长度之和，它的最小值就是 PA +PB 的最小值．设点 A 关于 x 轴的对称点为 A ′，则 PA ＝PA ′， 因此，求 PA +PB 的最小值，只需求 PA ′+PB 的最小值，由两点之间，线段最短可得，PA ′+PB 的最小值为线段 A ′B 的长度．为求 A ′B 我们可以构造直角三角形 A ′CB ，因为 A ′C ＝3，CB ＝3，所以 A ′ B ＝3 2，即原式的最小值为 3 2解答问题：（1）代数式 + (x — 2)2 + 9的值可以看成平面直角坐标系中点 P （x ，0）与点 A （1，1）、点 B （2，3） 的距离之和（填写点 B 的坐标）；（2）代数式 x 2 + 49 + x 2 — 12x + 37的最小值为 10 ．【思路点拨】（1）模仿例题即可解决问题；（2）用转化的思想思考问题即可；【解析】解：（1）由题意可知，点 B 坐标为（2，3）；故答案为（2，3）．（2） x 2 + 49 + x 2 — 12x + 37 = x 2 + 72 + (x — 6)2 + 12，求 x 2 + 49 + x 2 — 12x + 37的最小值，相当于在 x 轴上找一点 P （x ，0），使得 P 到 A （0，7），B （6，1）的距离之和的最小值，设点 A 关于 x 轴的对称点为 A ′，则 PA ＝PA ′，因此，求 PA +PB 的最小值，只需求 PA ′+PB 的最小值， 由两点之间，线段最短可得，PA ′+PB 的最小值为线段 A ′B 的长度．为求 A ′B 我们可以构造直角三角形 A ′CB ，因为 A ′C ＝6，CB ＝8，所以 A ′B ＝10，即原式的最小值为 10．故答案为 10．【点睛】本题考查轴对称﹣最短问题，勾股定理等知识，解题的关键是学会用数形结合的思想解决问题，属于中考常考题型．5.如图1，在平面直角坐标系中，点D 的横坐标为4，直线l1：y＝x+2 经过点D，分别与x、y 轴交于点A、B两点．直线l2：y＝kx+b经过点D及点C（1，0）．（1）求出直线l2 的解析式．（2）在直线l2 上是否存在点E，使△ABE 与△ABO 的面积相等，若存在，求出点E 的坐标，若不存在，请说明理由．（3）如图2，点P为线段AD上一点（不含端点），连接CP，一动点H从点C出发，沿线段CP以每秒2 个单位的速度运动到P，再沿线段PD 以每秒2 2个单位的速度运动到D 后停止，求P 点在整个运动过程的最少用时．【思路点拨】（1）利用C，D 两点坐标代入y＝kx+b，解方程组即可解决问题；（2）存在．如图1 中，作OE∥AB 交CD 于E．由AB∥OE，可得S△ABE＝S△ABO，构建方程组求出点E 坐标即可；（3）如图2 中，作DM∥AC，PH⊥DM 于H，CH′⊥DM 于H′交AD 于P′．由题意P 点在整个运2 2 2动过程的时间t = PC+ PD = 1 PC + PD MDA ＝∠BAO ＝45°，推出PH = P D t = 1PC +PH ）， 2 2（ 2 ），易知∠ 2，推出 2（ 根据此线段最短可知，当点 P 与 P ′，点 H 与 H ′共线时，t 的值最小，最小值= 1CH ′； 【解析】解：（1）由题意 A （﹣2，0），B （0，2），D （4，6），C （1，0），则 有 k + b = O ，4k + b = 6解 得 k = 2 ，b =— 2∴直线 l 2 的解析式为 y ＝2x ﹣2．（ 2 ） 存 在 ． ① 当 点 E 在 线 段 CD 上 时 ， 如 图 1 中 ， 作 OE ∥ AB 交 CD 于E ．∵AB ∥OE ，∴S △ABE ＝S △ABO ，∵直线 OE 的解析式为 y ＝x ，y = x 由 y = 2x — 2 ∴E （2，2）．，解得 x = 2， y = 2②当点 E ′在线段 CD 的延长线上时，由 y = x + 4 ，解得 x = 6 ，∴E ′（6，10）．y = 2x — 2y = 1O 综上所述，满足条件的点 E 坐标为（2，2）或（6，10）．（3）如图 2 中，作 DM ∥AC ，PH ⊥DM 于 H ，CH ′⊥DM 于 H ′交 AD 于 P ′．2 2 2 22由题意 P 点在整个运动过程的时间 t =PC + PD = 1（PC + PD 2 2 2∵A （﹣2，0），B （0，2），∴OA ＝OB ，∴∠MDA ＝∠BAO ＝45°，∴PH =PD ∴t = 1（PC +PH ）， 根据此线段最短可知，当点 P 与 P ′，点 H 与 H ′共线时，t 的值最小，最小值= 1CH ′＝3s∴P 点在整个运动过程的最少用时为 3s ．【点睛】本题考查一次函数综合题、待定系数法、平行线的性质、等高模型、垂线段最短等知识，解题的关键是灵活运用所学知识解决问题，学会用转化的思想思考问题，属于中考压轴题．， ），。

专题一.线段和（差）的最值问题【知识依据】1．线段公理——两点之间，线段最短；2．对称的性质——①关于一条直线对称的两个图形全等；②对称轴是两个对称图形对应点连线的垂直平分线；3．三角形两边之和大于第三边；4．三角形两边之差小于第三边；5、垂直线段最短。

一、已知两个定点：1、在一条直线m 上，求一点P ，使PA+PB 最小；（1）点A 、B 在直线m 两侧：（2）点A 、B 在直线同侧：A 、A ’ 是关于直线m 的对称点。

2、在直线m 、n 上分别找两点P 、Q ，使PA+PQ+QB 最小。

（1）两个点都在直线外侧：P m A B m A B m A BPm A B A'n m A B Q P n m A B P'Q'（2）一个点在内侧，一个点在外侧：（3）两个点都在内侧：（4）、台球两次碰壁模型变式一：已知点A 、B 位于直线m,n 的内侧，在直线n 、m 分别上求点D 、E 点，使得围成的四边形ADEB 周长最短.变式二：已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.n m A B QP n m A B B'Q P nm A B B'A' n m A B m n A B E D m n A B A'B'm n A P Q m n A A'二、一个动点，一个定点：（一）动点在直线上运动： 点B 在直线n 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ）1、两点在直线两侧：2、两点在直线同侧：（二）动点在圆上运动：点B 在⊙O 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ）1、点与圆在直线两侧：2、点与圆在直线同侧：m n A P m n A B m n A Pm n A A'B m O A P'P m O B A B' m O A P m O A B A'三、已知A 、B 是两个定点，P 、Q 是直线m 上的两个动点，P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点，使得PA+PQ+QB 的值最小。