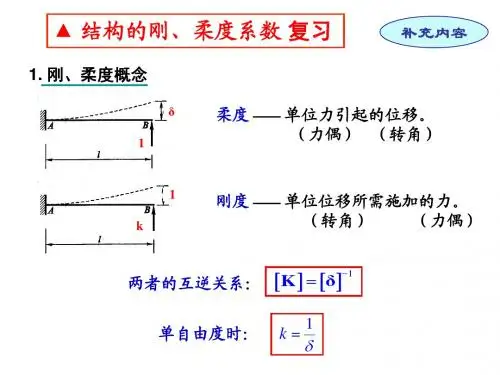
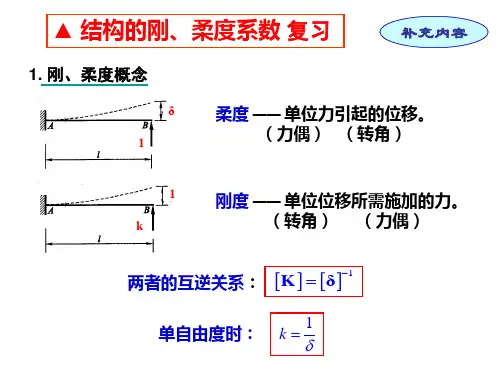
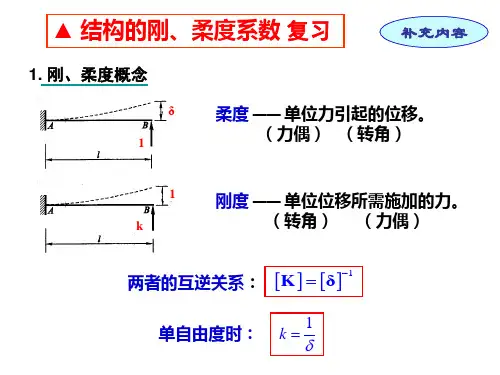
柔度系数

结构力学柔度计算公式结构力学柔度计算公式是结构力学领域的重要公式之一。

它可以用来计算结构的柔度，也就是结构的变形能力。

在结构设计和分析中，柔度是一个非常重要的参数，它可以帮助工程师评估结构的稳定性和安全性。

本文将详细介绍结构力学柔度计算公式的含义、应用和计算方法。

一、什么是柔度？柔度是指结构在受到外部载荷作用时所产生的变形量与外部载荷之间的比值。

柔度是结构力学中的一个重要概念，它可以帮助工程师评估结构的变形能力和稳定性。

柔度越大，结构的变形能力就越强，但是结构的稳定性也越差。

相反，柔度越小，结构的变形能力就越小，但是结构的稳定性也越好。

二、柔度计算公式的含义在结构力学中，柔度计算公式可以用来计算结构的柔度。

结构的柔度可以表示为：F = kx其中，F表示结构所受到的外部载荷，k表示结构的柔度系数，x表示结构的变形量。

柔度系数k是一个常数，它与结构的材料、几何形状和截面尺寸等因素有关。

柔度计算公式的含义可以理解为：当结构所受到的外部载荷为F时，结构的变形量x与载荷F之间的关系可以用柔度系数k来表示。

柔度系数k越小，结构的变形量x就越小，结构的稳定性就越好，但是结构的变形能力也越小。

三、柔度计算公式的应用柔度计算公式在结构设计和分析中有着广泛的应用。

它可以用来评估结构的稳定性、变形能力和安全性。

在结构设计中，工程师需要根据结构的使用要求和设计条件来确定柔度系数k的取值。

柔度系数k的取值对于结构的稳定性和变形能力有着重要的影响。

在结构分析中，柔度计算公式可以用来计算结构的变形量和应力分布。

工程师可以根据结构的柔度系数k和外部载荷F来计算结构的变形量x。

然后，根据结构的变形量x和结构的几何形状、材料等因素来计算结构的应力分布。

这些分析结果可以帮助工程师评估结构的安全性和稳定性，从而确定结构的设计方案。

四、柔度计算公式的计算方法柔度计算公式的计算方法比较简单。

首先，需要确定结构的柔度系数k。

柔度系数k可以根据结构的材料、几何形状和截面尺寸等因素来确定。

柔度系数符号1. 什么是柔度系数？柔度系数是一种用于描述材料柔软性的物理量。

它是指材料在受到外力作用后发生变形的程度。

柔度系数通常用符号表示，可以用于定量比较不同材料的柔软性。

2. 柔度系数的符号表示柔度系数一般用小写字母表示，常见的符号有：•ε：表示材料的应变（strain），是指材料在受到外力作用后相对于初始状态的变形程度。

应变可以是线性的，也可以是非线性的，取决于材料的性质。

•σ：表示材料的应力（stress），是指材料单位面积上受到的力的大小。

应力可以是拉伸应力、剪切应力等不同类型的应力。

•E：表示材料的弹性模量（Young’s modulus），是指材料在拉伸或压缩时的应力和应变之间的比例关系。

弹性模量可以用来描述材料的刚度。

•G：表示材料的剪切模量（shear modulus），是指材料在剪切应力下的变形程度。

剪切模量可以用来描述材料的刚度。

•ν：表示材料的泊松比（Poisson’s ratio），是指材料在拉伸或压缩时在垂直方向上的收缩或伸长程度与拉伸方向上的应变之间的比例关系。

3. 柔度系数的计算方法柔度系数可以通过应力和应变之间的关系来计算。

对于线性弹性材料，柔度系数可以用弹性模量和泊松比来表示：柔度系数 = 弹性模量 / (2 * (1 + 泊松比))对于非线性材料，柔度系数的计算相对复杂，需要考虑材料的应力-应变曲线。

4. 柔度系数的应用柔度系数在材料科学和工程中有广泛的应用。

它可以用来比较不同材料的柔软性，帮助工程师选择合适的材料。

柔度系数还可以用来设计和优化结构，以确保其在受力时具有良好的变形性能。

在纺织工业中，柔度系数可以用来评估织物的柔软性和弹性。

这对于设计舒适的服装和纺织品非常重要。

在建筑工程中，柔度系数可以用来评估建筑材料的变形能力和抗震性能。

它可以帮助工程师设计出更安全、更稳定的建筑结构。

在医学领域，柔度系数可以用来评估组织和器官的柔软性。

例如，在眼科学中，柔度系数可以用来评估角膜的弹性，帮助医生诊断角膜病变。

柔度系数符号摘要：1.柔度系数的定义和意义2.柔度系数的符号表示3.柔度系数在工程中的应用4.提高柔度系数的方法5.总结正文：柔度系数是一个用于描述物体在受力过程中形变程度的物理量，它反映了材料的柔软程度或刚度。

在工程设计中，了解和掌握柔度系数至关重要，因为它可以直接影响到产品的使用寿命、性能和稳定性。

一、柔度系数的定义和意义柔度系数（Symbol: μ）是用来衡量材料在受力时的变形能力的物理量，它与材料的弹性模量（E）和泊松比（ν）有密切关系。

柔度系数μ越小，材料的柔软程度越高，抗变形能力越强；反之，μ越大，材料的刚度越高，抗变形能力越弱。

二、柔度系数的符号表示柔度系数通常用希腊字母μ（mu）表示，单位为1/Pa（帕斯卡）。

在实际工程中，柔度系数通常用符号C表示，单位为1/N（牛顿）。

它们之间的关系为：C = μ * ΔL / ΔF，其中ΔL表示受力后的变形量，ΔF表示所施加的力。

三、柔度系数在工程中的应用1.结构设计：在建筑、桥梁、机械等结构设计中，通过计算和比较不同材料的柔度系数，可以选择更适合的结构材料，提高结构的稳定性和使用寿命。

2.零部件选型：在机械零部件选型中，了解各部件的柔度系数，可以有效降低系统的振动、噪声和磨损，提高传动效率。

3.材料研究：通过研究材料的柔度系数，可以指导新材料的开发和优化，满足不同工程领域的应用需求。

四、提高柔度系数的方法1.选用高弹性模量的材料：提高材料的弹性模量可以降低柔度系数，提高抗变形能力。

2.调整材料结构：如采用纤维增强、网格结构等方式，可以提高材料的整体刚度，降低柔度系数。

3.改进设计方法：在结构设计中，采用合理的设计方法和优化算法，可以降低结构的柔度系数，提高稳定性。

五、总结柔度系数是一个重要的工程参数，它直接影响到产品的使用寿命、性能和稳定性。

了解和掌握柔度系数的符号、定义和应用，对于工程设计和材料研究具有重要的指导意义。

柔度系数和柔度的关系
柔度系数和柔度之间存在密切的关系，它们在材料科学和工程
领域中都具有重要的意义。

首先，让我们来了解一下柔度系数。

柔度系数是用来描述材料
的柔软程度或者变形能力的物理量。

它通常用于描述弹性材料在受
力后的变形程度。

柔度系数越大，材料的柔软程度越高，它能够更
容易地发生形变。

柔度系数的大小与材料的弹性模量（刚度）有关，弹性模量越小，柔度系数越大。

柔度则是指材料的柔软性或者弯曲变形的能力。

柔度与柔度系
数密切相关，柔度系数大的材料具有较高的柔度，能够更容易地发
生形变或者弯曲。

在工程中，柔度系数和柔度都是材料设计和选择中重要的考量
因素。

例如，在设计弹簧或者减震器时，需要考虑材料的柔度系数，以确保其具有合适的变形能力和回弹性能。

另外，对于柔性电子产
品或者柔性传感器，材料的柔度和柔度系数也是关键因素，影响着
产品的性能和可靠性。

总的来说，柔度系数和柔度之间的关系可以简单地概括为，柔度系数描述了材料的柔软程度，而柔度则是材料具体的柔软性或者弯曲变形的能力。

它们共同影响着材料在受力后的变形行为和性能表现。

结构力学柔度计算公式
柔度系数为刚度系数的倒数，计算方法为：刚度系数为EA/L，其中E—杆件的弹性模量，A—杆件截面面积，L—杆件的长度。

柔度系数为：1/(EA/L)=L/EA
柔度系数，表示的是物体杆件在单位力的作用下，杆件顶部产生的位移，在单自由度体系或振动方程互不耦合的多自由体系，其值与刚度系数互为倒数。

刚度系数是用以描述材料在外力作用下弹性变形形态的基本物理量。

更通俗的讲是使杆端产生单位位移时所需施加的杆端力。

物体杆件在单位力的作用下，杆件顶部产生的位移，在单自由度体系或振动方程互不耦合的多自由体系，其值与刚度系数互为倒数。

柔度=uL/i（u为长度系数，与杆的约束形式有关；L为杆长；i为杆截面的惯性半径）。

由于轧机零部件间存在的间隙和接触不均匀是一个不稳定因素，弹性曲线的非线性部分是经常变化的，在实际生产中，为了消除非线性段的影响，往往采用人工零位法。

刚度系数和柔度系数的关系嘿，朋友们！今天咱来聊聊刚度系数和柔度系数这俩家伙呀！你说这刚度系数呢，就像是个硬骨头，特别倔强，不容易变形。

想象一下，那就是一根特别结实的铁棍，你怎么掰它都很难让它弯曲。

它呀，代表着材料抵抗变形的能力，越强就越难让它有啥变化。

而柔度系数呢，简直就是刚度系数的反义词啦！它就像个面团似的，可以随意被揉捏变形。

它反映的是材料容易变形的程度呀。

咱举个例子哈，比如说弹簧。

那弹簧就是柔度系数比较大的典型。

你轻轻一拉，它就能变长好多，很容易就变形啦。

但要是换成一块铁板，那可就不一样咯，你得使多大劲才能让它有点变化呀，这就是刚度系数大的表现。

你说这俩家伙是不是很有意思呀？它们就像一对欢喜冤家。

有时候我们需要刚度系数大的材料，比如建大桥呀，那可不能软了吧唧的，得稳稳当当的。

可有时候呢，又需要柔度系数大的，像一些需要缓冲的地方，就得能屈能伸。

刚度系数和柔度系数的关系呀，就好像白天和黑夜，相互对立又相互依存。

没有绝对的好与坏，只有在合适的地方发挥合适的作用。

咱在生活中不也常常遇到这样类似的情况嘛！有时候我们得像刚度系数一样坚定，不轻易被外界改变；可有时候呢，又得像柔度系数一样灵活，能适应各种变化。

比如说在职场上，该坚持原则的时候就得刚，可遇到一些特殊情况也得学会变通呀。

再想想，人际关系不也是这样嘛！和有些人相处，你就得硬气点，不能随便被欺负；可和另一些人呢，就得柔和点，不然关系不就僵啦。

所以呀，我们得学会把握好这个度，根据不同的情况灵活运用刚度系数和柔度系数的特点。

不能一味地刚，也不能一味地柔，得刚柔并济才行呀！这就好像走路，一条腿太硬走不快，一条腿太柔又走不稳，得两条腿配合好了，才能稳稳当当往前走不是？总之，刚度系数和柔度系数这俩概念虽然是在物理学里的，但咱在生活中也能找到好多类似的道理呀。

我们要学会在不同的场景下，发挥出它们的优势，让我们的生活更加美好，更加顺利呀！你们说是不是这个理儿呢？。

高速动车组柔度系数测定及方法研究柔度系数是车辆设计的重要参数，关系到车辆的抗侧滚性能，对车辆运行的限界安全有直接影响。

针对高寒防风沙动车组，提出了基于整车振动模拟试验台的柔度系数的测定方法，并运用位姿反解的方法对作动器执行命令进行解算，实现试验台的加载；区别于传统的测定手段，该方法可得到试验过程中车体、转向架转角的连续数据，是一种动态的测定手段，获取柔度系数随车体、转向架侧滚角度变化的规律；试验结果表明，被试车辆柔度系数最大值0.285，符合UIC505标准的要求，同时也为高寒防风沙动车组的设计提供数据积累和技术支撑。

标签：高速动车组；整车振动模拟试验台；柔度系数；姿态解算；试验方法1 前言随着我国轨道车辆出口项目的逐年增加，为满足车辆出口要求，国内的标准需进一步与国际标准接轨，或需采用出口目标国的标准执行；车辆柔度系数是车辆运行安全、舒适性的重要指标，是欧洲（EN）及国际铁路联盟（UIC）标准执行的重要参数，柔度系数的测定尤为重要。

传统的测定方法有重锤法、倾角法、加速度传感法，其中重锤法、倾角法均需采用不同高度的垫块进行超高模拟，但重锤法受限于垫块的尺寸，无法实现柔度系数的动态测定，且试验精确较低；倾角法则受制于所采用角度传感器的精度，不确定因素较大；加速度传感器法，依托于车辆的线路运行工况，且须控制车辆在低速运行状态，降低车辆惯性加速度的影响，试验结果精度低。

针对此类问题，本文提出一种依托整车振动模拟试验台进行柔度系数测定的方法，可实现柔度系数的连续性测定，试验的精度高。

2 整车振动模拟试验台本试验方法基于中车青岛四方股份公司的整车振动模拟试验台，该试验台是用于研究车辆装配状态下的特性参数，再现车辆在线路运营时的振动状态，为车辆的振动性能设计优化提供试验平台，为转向架设计验证提供试验手段。

本试验台由机械系统、控制系统、液压系统、试验测试工具组件等组成。

机械系统包括四个运动平台、模拟车体加载平台、反应基座等；控制系统包括Flextest200控制机柜、主机和控制线缆等；液压系统由液压油源（六台，约3000升/分钟）、液压作动器（31个）、液压管路及阀、（5个）分油控制单元和多个蓄能器等；试验测试工具组件包括六自由度力传感器（4个）、位移传感器和加速度传感器、SOMAT数采设备、试验车轴及多种夹具、标定框架工装及砝码等。

柔度系数符号
【原创实用版】
目录
1.柔度系数的定义与符号表示
2.柔度系数的应用领域
3.柔度系数的计算方法与示例
4.柔度系数的重要性
正文
柔度系数是材料科学中一个重要的概念，它用来衡量材料在外力作用下发生形变的难易程度。

柔度系数的符号通常用字母 G 表示，它反映了
材料在一定应力下的应变能力。

柔度系数的应用领域非常广泛，它不仅可以用来研究金属、塑料、橡胶等材料的力学性能，还可以用于分析桥梁、建筑物等工程结构的稳定性和耐久性。

此外，柔度系数在航空航天、汽车制造等产业领域也有着广泛的应用。

柔度系数的计算方法通常是通过实验数据来获得的。

实验过程中，会将材料置于一定的应力条件下，然后测量其形变量。

根据胡克定律，形变量与应力成正比，因此可以通过计算形变量与应力的比值来得到柔度系数。

例如，对于一根金属棒，在施加 100 牛顿的拉力时，其长度会发生 1 毫米的伸长。

那么，这根金属棒的柔度系数就是 100 牛顿/毫米。

柔度系数的重要性在于，它可以帮助工程师在设计工程结构时，选用具有合适柔度特性的材料。

对于承受压力较大的结构，应选择柔度系数较小的材料，以保证结构的稳定性；而对于需要具有良好的抗震性能的结构，应选择柔度系数较大的材料，以提高结构的耐久性和适应性。

第1页共1页。

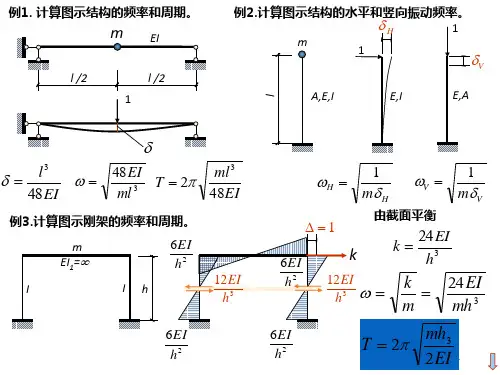
柔度系数法建立振动方程的若干例题陈奎孚整理中国农业大学应用力学系柔度系数法是建立振动方程的一种重要方法，它对弹簧质量和集中质量梁这类系统使用起来比较方便。

本报告给出若干示例。

1. 单自由度例1 如图1(a)所示的简支外伸梁,AB 为弹性梁，质量不计，BC 为刚性杆，线密度为l ρ。

求微幅振动的固有频率。

解: 系统为一个自由度, 选择图1 (b)所示的q 为广义坐标。

中力Bx'F 和By 'F 对AB 梁的变形没有贡献，有贡献的只有弯矩M '。

根据材料力学简支梁一端加载弯矩的公式有3lM EIq '=BC 梁是绕B 作定轴转动，因此313'32l l EI M M lρq q ⎛⎫=-=-=- ⎪⎝⎭ 即得微分方程4720l EIlq q ρ+=系统的固有频率为p =例2如图2(a)所示的简支梁。

右端为弹性支撑, 348EIk l =，跨中有一集中质量。

用柔度法建立微分方程，并求固有频率。

I ()()w t F mw t d d =-=- (#)其中柔度系数d 的物理意义如图3(a)所示, 它可以分解为图 3 (b)和(c)的柔度迭加。

由材料力学有148l EId =, 而21111224192l k k EI d ⎛⎫=⨯⨯== ⎪⎝⎭。

因此33312548192192l l l EI EI EId d d =+=+=代入方程(#)式得振动微分方程319205EI mw w l+= 固有频率为p =例3如图4(a)所示的简支折杆上端有一集中质量，用柔度法建立微分方程，并求固有频率。

解: 结构的变形、质量的运动如图4(b)所示。

集中质量处的变形方程为I ()()w t F mw t d d =-=- (#)其中柔度系数d 的物理意义如图5(a)所示。

它可以分解为两个分量:水平梁固定不动情况下的悬臂梁挠度(图5(b));因水平横梁弯曲引起竖直梁的刚性偏移(图5(b))。