公务员数学推理题十大规律大总结
- 格式:doc
- 大小:5.81 MB
- 文档页数:24
图形推理的两大灵魂是 数量关系 和 图形转动 。
牢牢把握住这两大灵魂就基本把握了图形推理题目。
在这两大灵魂统帅下的十大基本规律,是每个想要在公考中取得优异成绩的考生必须系统熟练把握的。
下面小考啦来为大家举例说明。
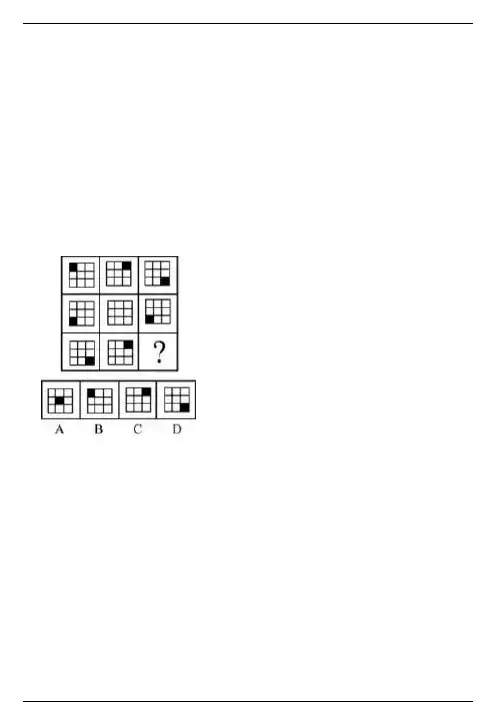
例1:解析:B方法一: 从图形旋转的角度来分析这个题目。
顺时针方向看,会发现黑色小方框在作顺时针旋转。
具体的说,第一行三个图形中,黑色小方框在作顺时针旋转;然后从第三列往下看,发现黑色小方框仍然在作顺时针旋转。
整个观察顺序是:第一行,从左向右,到了第三个图形,从上往下;到了右下角的图形,从右往左,到了左下角,再从下往上。
如果选择逆时针方向分析,会发现黑色小方框在作逆时针旋转。
最后同样得到答案B。
方法二: 从图形的数量关系来分析这个题目。
图中含有黑色小方框的图形是成对出现的。
因此答案为B。
例2:解析:A第一列,从下往上,三个图形中,图形外的线段数量分别是1,3,5。
第二列,从上往下,三个图形中,图形外的线段数量分别是7,9,11。
第三列,从下往上,三个图形中,图形外的线段数量分别是13,15,17。
从列的角度来考察的。
分析这类题目的时候,如果从行的角度去考察,难以发现规律,不妨改变一下角度,从列的角度去考察。
本题每个图形出头线段数目如下图:例3:解析:D这个题目看从什么角度来分析。
如果把第一行三个小图形放在一起分析,然后把第二行三个图形放在一起分析,就很难找到正确的答案来。
如果把第一列的三个图形放在一起分析,把第二列的三个图形放在一起分析,就比较容易找出答案来。
整个题目的规律是:从列方向上来看,第一个图形的直线边数等于下面两个图形的边数之和。
以前考试的题目和参考书上的练习题目大多是从行的方向来考察的,这次考题换了一个角度。
根据前面几道题的特点来看,从列方向的角度来设计题目,应该是命题者的真实意图例4:解析:A第一行的三个图形,封闭部分的数量分别是 3,2,3和3 2 3=8;第二行的三个图形,封闭部分的数量分别是1,3,4和1 3 4=8;按照这个规律,第三行三个图形封闭部分数量之和应该是8。

十大经典逻辑推理
1.倒推法:从结果推出原因,逆向思维。
2. 类比法:将不同领域的问题进行类比,找到相似之处,推导出解决问题的方法。
3. 归纳法:从一些特定的事实或现象中,总结出普遍规律,进而推导出结论。
4. 演绎法:从一般原则出发,逐步推导出具体的结论。
5. 等价转换法:将一个命题转换成另一个与之等价的命题,从而推出结论。
6. 假设法:假设某些条件成立,然后根据这些条件推导出结论。
7. 对比法:将两个相似或相反的事物进行对比,从中得到结论。
8. 消解法:找出命题中的矛盾点,通过消解矛盾点来推导出结论。
9. 逆否命题法:将命题的逆命题和否定命题进行推导,从而得出结论。
10. 经验法则法:依据过去的经验和常识,推导出结论。
- 1 -。

图形专项突破中绝大多数例题都是公考真题,命题标准,指导性明确,具有很高的价值。
图形专项突破编写系统,几乎含盖图形推理全部类型的题目。
图形推理的两大灵魂是数量关系和图形的转动。
牢牢把握住这两大灵魂就根本把握了图形推理题目。
在这两大灵魂统帅下的十大根本规律,是每个想要在公考中取得优异成绩的考生必须系统熟练把握的。
图形推理的两大灵魂:数量关系和图形的转动。
这里以2007年国家公务员考试真题为例子来说明图形推理的两大灵魂。
1.答案:B分析:方法一,从图形旋转的角度来分析这个题目。
顺时针方向看,会发现黑色小方框在作顺时针旋转。
具体的说,第一行三个图形中,黑色小方框在作顺时针旋转;然后从第三列往下看,发现黑色小方框仍然在作顺时针旋转。
整个观察顺序是:第一行,从左向右,到了第三个图形,从上往下;到了右下角的图形,从右往左,到了左下角,再从下往上。
如果选择逆时针方向分析,会发现黑色小方框在作逆时针旋转。
最后同样得到答案B。
方法二,从图形的数量关系来分析这个题目。
图中含有黑色小方框的图形是成对出现的。
因此答案为B。
2.答案:A分析:第一列,从下往上,三个图形中,图形外的线段数量分别是1,3,5。
第二列,从上往下,三个图形中,图形外的线段数量分别是7,9,11。
第三列,从下往上,三个图形中,图形外的线段数量分别是13,15,17。
从列的角度来考察的。
分析这类题目的时候,如果从行的角度去考察,难以发现规律,不妨改变一下角度,从列的角度去考察。
此题每个图形出头线段数目如以下图:3.答案:D分析:这个题目看从什么角度来分析。
如果把第一行三个小图形放在一起分析,然后把第二行三个图形放在一起分析,就很难找到正确的答案来。
如果把第一列的三个图形放在一起分析,把第二列的三个图形放在一起分析,就比较容易找出答案来。
整个题目的规律是:从列方向上来看,第一个图形的直线边数等于下面两个图形的边数之和。
以前考试的题目和参考书上的练习题目大多是从行的方向来考察的,这次考题换了一个角度。

备考规律一:等差数列及其变式【例题】7,11,15,()A.19B.20C.22D.25【答案】A选项【解析】这是一个典型的等差数列,即后面的数字与前面数字之间的差等于一个常数。
题中第二个数字为11,第一个数字为7,两者的差为4,由观察得知第三个与第二个数字之间也满足此规律,那么在此基础上对未知的一项进行推理,即15+4=19,第四项应该是19,即答案为A.(一)等差数列的变形一:【例题】7,11,16,22,()A.28B.29C.32D.33【答案】B选项【解析】这是一个典型的等差数列的变形,即后面的数字与前面数字之间的差是存在一定的规律的,这个规律是一种等差的规律。
题中第二个数字为11,第一个数字为7,两者的差为4,由观察得知第三个与第二个数字之间的差值是5;第四个与第三个数字之间的差值是6.假设第五个与第四个数字之间的差值是X,我们发现数值之间的差值分别为4,5,6,X.很明显数值之间的差值形成了一个新的等差数列,由此可以推出X=7,则第五个数为22+7=29.即答案为B选项。
(二)等差数列的变形二:【例题】7,11,13,14,()A.15B.14.5C.16D.17【答案】B选项【解析】这也是一个典型的等差数列的变形,即后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种等比的规律。
题中第二个数字为11,第一个数字为7,两者的差为4,由观察得知第三个与第二个数字之间的差值是2;第四个与第三个数字之间的差值是1.假设第五个与第四个数字之间的差值是X.我们发现数值之间的差值分别为4,2,1,X.很明显数值之间的差值形成了一个新的等差数列,由此可以推出X=0.5,则第五个数为14+0.5=14.5.即答案为B选项。
(三)等差数列的变形三:【例题】7,11,6,12,()A.5B.4C.16D.15【答案】A选项【解析】这也是一个典型的等差数列的变形,即后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种正负号进行交叉变换的规律。
公务员数字推理技巧总结精华版数字推理技巧总结备考规律一:等差数列及其变式(后一项与前一项的差 d 为固定的或是存在一定规律(这种规律包括等差、等比、正负号交叉、正负号隔两项交叉等)(1) 后面的数字与前面数字之间的差等于一个常数。
如7,11,15,( 19 ) (2)后面的数字与前面数字之间的差是存在一定的规律的,这个规律是一种等差的规律。
如7,11,16,22,( 29 )(3)后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种等比的规律。
如7,11,13,14,( 14.5 )(4)后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种正负号进行交叉变换的规律。
【例题】7,11,6,12,( 5 )(5) 后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种正负号每“相隔两项”进行交叉变换的规律。
【例题】7,11,16,10,3,11,(20 )备考规律二:等比数列及其变式(后一项与除以前一项的倍数 q 为固定的或是存在一定规律(这种规律包括等差、等比、幂字方等)(1)“后面的数字”除以“前面数字”所得的值等于一个常数。
【例题】4,8,16,32,( 64 )(2)后面的数字与前面数字之间的倍数是存在一定的规律的,倍数加1。
【例题】4,8,24,96,( 480 )(3)后面的数字与前面数字之间的倍数是存在一定的规律的,倍数乘 2【例题】4,8,32,256,( 4096 )(4)后面的数字与前面数字之间的倍数是存在一定的规律的,倍数为 3 的n 次方。
【例题】2,6,54,1428,( 118098 )(5)后面的数字与前面数字之间的倍数是存在一定的规律的,“倍数”之间形成了一个新的等差数列。
【例题】2,-4,-12,48,(240 )备考规律三:“平方数”数列及其变式(an=n2+d,其中d为常数或存在一定规律)(1) “平方数”的数列【例题】1,4,9,16,25,36 ,49,64,81,100,121,144,169,196(2)每一个平方数减去或加上一个常数【例题】 0,3,8,15,24,(35 )【例题变形】2,5,10,17,26,(37 )(3) 每一个平方数加去一个数值,而这个数值本身就是有一定规律的。

公务员常见图形推理规律总结一组图(跳着看)、九宫格(竖着看、米字形、S型)元素组成相同-位置规律1.平移方向:上下、左右、斜对角线绕圈:顺逆时针步数:恒定、等差16宫格可以考虑内外圈分开看2.旋转、翻转旋转:顺逆时针45度、90度、180度翻转:左右翻转竖轴对称上下翻转:横轴对称(注意上下翻的横着画)3.从头跑、折返跑元素组成相似-样式规律(线条重复出现)1.加减同异相加相减求同求异2.黑白运算得出黑+白=?这样的运算(相同位置运算)区分:黑块数量相同优先平移,黑块数量不同,优先黑白运算注意:位置和样式的复合考法分类:一个图形里有规律,几个图形规律一样元素组成不相同、不相似-属性规律1.对称性轴对称(对称轴方向、数量、对称轴间关系平行/垂直、对称轴是不是自己带的);中心对称;轴对称+中心对称2.曲直性全曲全直、半曲半直3.开闭性完整的图形留了个小开口注:五角星轴对称图形,有5条对称轴,不是中心对称图形元素组成不相同、不相似-数量规律考点:点、线、面、素、角1.点数量切点也属于交点,端点不是交点特征:线条交叉明显、乱糟糟一团线交叉、相切较多与圆相交的交点2.线数量2.1直线和曲线直线数特征:多边形、单一直线数量、关系(平行/垂直,比如第一条边与最后一条边,有时还需考虑方向)曲线数特征:曲线图形特殊:曲-直数量、曲+直数量、竖线数量、横线数量2.2一笔画问题特征图、图形出现多端点图形、多三角形图案,考虑数笔画数一笔画:线条之间连通、奇点数=0或2(端点、丁字口)多笔画笔画数=奇点数/2(奇点数一定是偶数个)常见:一笔画:五角星、日及其变形、圆相切、相交(圆相切和相交的点均发射出偶数条线,不是奇点)二笔画:田及其变形3.面数量—图形被分割、封闭面明显、生活化图形、粗线条图形中留空白区域面的数量、形状、最大的面、最小的面4.素数量4.1小元素特征-多个独立小图形元素种类、个数(个数组成形式311、221)、替换(一种图形是一个数值或一种图形=几个另一种图形)4.2部分数特征-生活化图形、黑色粗线条图形(线条与线条连在一起叫做一部分)5.角数量(直角、钝角、锐角)扇形、改造图、折线图有直角优先关注直角注意:综合几种性质(如对称轴数量和面数量相等、曲直+面)特殊规律1.功能元素点:观察点对其他图形的标记作用、观察点与点之间的关系箭头:观察箭头的指向性、观察箭头与箭头之间的关系2.图形间关系—每幅图都是两个元素或者几个封闭空间连在一起相离、相压、相交(1)相交于面相交面的形状、面积等(2)相交于点相交点的位置(上下左右和内外)(3)相交于边相交于边的数量、相交边的样式(相交边是长边、短边;包含相交、交错相交;曲直)其他规律汉字、数字、字母:笔画数、线、面、部分、属性空间重构相对面同时出现为错误选项相对面-同行或同列相隔一个面、Z字形两端三视图三视图都是平面图原图有线就有线,原图没线就没线。

公务员行测数字推理必知的30个规律一、当一列数中出现几个整数,而只有一两个分数而且是几分之一的时候,这列数往往是负幂次数列。
【例】1、4、3、1、1/5、1/36、( )92 124 262 343二、当一列数几乎都是分数时,它基本就是分式数列,我们要注意观察分式数列的分子、分母是一直递增、递减或者不变,并以此为依据找到突破口,通过“约分”、“反约分”实现分子、分母的各自成规律。
【例】1/16 2/13 2/5 8/7 4 ()3三、当一列数比较长、数字大小比较接近、有时有两个括号时,往往是间隔数列或分组数列。
【例】33、32、34、31、35、30、36、29、( )A. 33B. 37C. 39四、在数字推理中,当题干和选项都是个位数,且大小变动不稳定时,往往是取尾数列。
取尾数列一般具有相加取尾、相乘取尾两种形式。
【例】6、7、3、0、3、3、6、9、5、( )五、当一列数都是几十、几百或者几千的“清一色”整数,且大小变动不稳定时,往往是与数位有关的数列。
【例】448、516、639、347、178、( )六、幂次数列的本质特征是:底数和指数各自成规律,然后再加减修正系数。
对于幂次数列,考生要建立起足够的幂数敏感性,当数列中出现6?、12?、14?、21?、25?、34?、51?、312?,就优先考虑43、112(53)、122、63、44、73、83、55。
【例】0、9、26、65、124、( )A. 165B. 193C. 217七、在递推数列中,当数列选项没有明显特征时,考生要注意观察题干数字间的倍数关系,往往是一项推一项的倍数递推。
【例】118、60、32、20、( )八、如果数列的题干和选项都是整数且数字波动不大时,不存在其它明显特征时,优先考虑做差多级数列,其次是倍数递推数列,往往是两项推一项的倍数递推。
【例】0、6、24、60、120、( )九、当题干和选项都是整数,且数字大小波动很大时,往往是两项推一项的乘法或者乘方的递推数列。

一、行测考试十大数据推理规律:①奇偶数规律:各个数都是奇数(单数)或偶数(双数)。
②等差:相邻数之间的差值相等,整个数字序列依列递增或递减。
③等比:相邻数之间的比值相等,整个数字序列依次递增或递减。
④二级等差:相邻数之间的差或比构成了一个等差数列。
⑤二级等比数列:相邻数之间的差或比构成一个等比数列。
⑥加法规律:前两个数之和等于第三个数。
⑦减法规律:前两个数之差等于第三个数。
⑧乘法(除法)规律:前两个数之乘积(或相除)等于第三个数。
⑨完全平方数:数列中蕴含着一个完全平方数序列,或明显、或隐含。
⑩混合型规律:由以上基本规律组合而成,可以是二级、三级的基本规律,也可能是两个规律的数列交叉组合成一个数列。
二、经典题型分类练习:1.等差数列例1:1, 4, 7, 10, 13,( )A.14B.15C.16D.172.等差数列的变式例1:3, 4, 6, 9,( ),18A.11B.12C.13D.143.“两项之和等于第三项”型例1:34, 35, 69, 104, ( )A.138B.139C.173D.179例2:…101102203305508( )1321…A.812B.814C.813D. 8114.等比数列例1:3, 9, 27, 81, ( )A.433B.342C.243D.1355.等比数列的变式例1:8, 12, 24, 60, ( )A.90B.120C.180D.240例2:8, 14, 26, 50, ( )A.104B.100C. 98D. 76例3:1/2, 1, 7/5, 13/9, ( )A. 17/13B. 19/15C. 21/17D. 23/196.平方型及其变式例1:1, 4, 9, ( ), 25, 36A.10B.14C.16D.20例2:1/2, 1, 5/7, ( ), 9/32A. 5/11B.7/11C.7/16D.9/167.利用“凑整法”求解例1:52+136+38+64的值为:A. 300B. 292C. 290D. 280例2:12.5×0.25×0.5×32的值为:( )A. 50.25B. 100C. 50D. 258.利用“尾数估算法”求解例1:425+683+544+828的值是:A. 2484B. 2482C. 2480D. 2478例2:1997+1998+1999+2000+2001A. 9993B. 9994C. 9995D. 9996。

数字推理的十大规律数字推理是通过对数字、数字关系、数字规律等进行分析、推理来解决问题的一种思维方式。
数字推理可以应用于数学、逻辑、信息处理、统计学等领域。
在数字推理中,存在着一些常见的规律,通过了解这些规律,我们可以更好地进行数字推理。
下面是数字推理中的十大常见规律:1. 自然数规律自然数规律是最基本的数字规律之一。
自然数由1开始依次递增,其中包含了所有整数。
我们可以通过对自然数序列的观察,进一步推导出一些数学规律。
例如,自然数序列的平方数规律:1, 4, 9, 16, 25, ...,可以看出平方数是自然数序列的某种特殊规律。
2. 等差数列规律等差数列是一种特殊的数字序列,其中相邻的数字之间的差值是相等的。
等差数列常用于数学题目、数列的求和问题等。
例如,2, 5, 8, 11, 14, ...,可以看出每个数字都比前一个数字增加了3。
3. 等比数列规律等比数列是一种特殊的数字序列,其中相邻的数字之间的比值是相等的。
等比数列常用于数学问题中,比如指数增长、连续复利等。
例如,2, 6, 18, 54, ...,可以看出每个数字都是前一个数字乘以3。
4. 斐波那契数列规律斐波那契数列是一个非常特殊的数列,其中每个数字都是前两个数字之和。
斐波那契数列在自然界中广泛存在,如植物的叶子排列、兔子繁殖等。
例如,1, 1, 2, 3, 5, 8, 13, ...,可以看出每个数字都是前两个数字之和。
5. 奇偶数规律奇偶数规律是数字推理中的一种常见规律。
奇数是整数中不能被2整除的数,偶数则是能被2整除的数。
例如,1, 3, 5, 7, 9, ...是奇数序列;2, 4, 6, 8, 10, ...是偶数序列。
6. 质数规律质数是只能被1和自身整除的自然数。
质数规律在密码学、因数分解等领域有重要应用。
例如,2, 3, 5, 7, 11, ...,可以看出每个数字都是质数。
7. 素数规律素数是指除了1和本身外没有其他除数的数,素数可以是质数或者合数。

图形推理最新十大规律技巧大全!(国考必备)图形推理的两大灵魂是数量关系和图形转动。
牢牢把握住这两大灵魂就基本把握了图形推理题目。
在这两大灵魂统帅下的十大基本规律,是每个想要在公考中取得优异成绩的考生必须系统熟练把握的。
下面小考啦来为大家举例说明。
例1:解析:B方法一:从图形旋转的角度来分析这个题目。
顺时针方向看,会发现黑色小方框在作顺时针旋转。
具体的说,第一行三个图形中,黑色小方框在作顺时针旋转;然后从第三列往下看,发现黑色小方框仍然在作顺时针旋转。
整个观察顺序是:第一行,从左向右,到了第三个图形,从上往下;到了右下角的图形,从右往左,到了左下角,再从下往上。
如果选择逆时针方向分析,会发现黑色小方框在作逆时针旋转。
最后同样得到答案B。
方法二:从图形的数量关系来分析这个题目。
图中含有黑色小方框的图形是成对出现的。
因此答案为B。
例2:解析:A第一列,从下往上,三个图形中,图形外的线段数量分别是1,3,5。
第二列,从上往下,三个图形中,图形外的线段数量分别是7,9,11。
第三列,从下往上,三个图形中,图形外的线段数量分别是13,15,17。
从列的角度来考察的。
分析这类题目的时候,如果从行的角度去考察,难以发现规律,不妨改变一下角度,从列的角度去考察。
本题每个图形出头线段数目如下图:例3:解析:D这个题目看从什么角度来分析。
如果把第一行三个小图形放在一起分析,然后把第二行三个图形放在一起分析,就很难找到正确的答案来。
如果把第一列的三个图形放在一起分析,把第二列的三个图形放在一起分析,就比较容易找出答案来。
整个题目的规律是:从列方向上来看,第一个图形的直线边数等于下面两个图形的边数之和。
以前考试的题目和参考书上的练习题目大多是从行的方向来考察的,这次考题换了一个角度。
根据前面几道题的特点来看,从列方向的角度来设计题目,应该是命题者的真实意图例4:解析:A第一行的三个图形,封闭部分的数量分别是 3,2,3和3 2 3=8;第二行的三个图形,封闭部分的数量分别是1,3,4和1 3 4=8;按照这个规律,第三行三个图形封闭部分数量之和应该是8。

备考规律一:等差数列及其变式【例题】7,11,15,()A.19B.20C.22D.25【答案】A选项【解析】这是一个典型的等差数列,即后面的数字与前面数字之间的差等于一个常数。
题中第二个数字为11,第一个数字为7,两者的差为4,由观察得知第三个与第二个数字之间也满足此规律,那么在此基础上对未知的一项进行推理,即15+4=19,第四项应该是19,即答案为A.(一)等差数列的变形一:【例题】7,11,16,22,()A.28B.29C.32D.33【答案】B选项【解析】这是一个典型的等差数列的变形,即后面的数字与前面数字之间的差是存在一定的规律的,这个规律是一种等差的规律。
题中第二个数字为11,第一个数字为7,两者的差为4,由观察得知第三个与第二个数字之间的差值是5;第四个与第三个数字之间的差值是6.假设第五个与第四个数字之间的差值是X,我们发现数值之间的差值分别为4,5,6,X.很明显数值之间的差值形成了一个新的等差数列,由此可以推出X=7,则第五个数为22+7=29.即答案为B选项。
(二)等差数列的变形二:【例题】7,11,13,14,()A.15B.14.5C.16D.17【答案】B选项【解析】这也是一个典型的等差数列的变形,即后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种等比的规律。
题中第二个数字为11,第一个数字为7,两者的差为4,由观察得知第三个与第二个数字之间的差值是2;第四个与第三个数字之间的差值是1.假设第五个与第四个数字之间的差值是X.我们发现数值之间的差值分别为4,2,1,X.很明显数值之间的差值形成了一个新的等差数列,由此可以推出X=0.5,则第五个数为14+0.5=14.5.即答案为B选项。
(三)等差数列的变形三:【例题】7,11,6,12,()A.5B.4C.16D.15【答案】A选项【解析】这也是一个典型的等差数列的变形,即后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种正负号进行交叉变换的规律。
公务员考试行测数字推理必知的30个规律公务员考试中,数字推理是一个非常重要的考试科目。
数字推理是指通过对数字、图形、文字等信息的分析和推理,得出正确的结论。
在数字推理中,有很多规律需要掌握。
本文将介绍公务员考试行测数字推理必知的30个规律。
一、数字规律1. 数字序列规律数字序列规律是指在一组数字中,数字之间的关系所遵循的规律。
常见的数字序列规律有等差数列、等比数列、斐波那契数列等。
2. 数字排列规律数字排列规律是指在一组数字中,数字的排列顺序所遵循的规律。
常见的数字排列规律有逆序、顺序、交替等。
3. 数字替换规律数字替换规律是指在一组数字中,数字被替换成其他数字的规律。
常见的数字替换规律有加减乘除、平方、开方等。
4. 数字组合规律数字组合规律是指在一组数字中,数字之间的组合所遵循的规律。
常见的数字组合规律有排列组合、加减乘除等。
二、图形规律图形旋转规律是指在一组图形中,图形的旋转方向和角度所遵循的规律。
常见的图形旋转规律有顺时针旋转、逆时针旋转等。
6. 图形翻转规律图形翻转规律是指在一组图形中,图形的翻转方向和方式所遵循的规律。
常见的图形翻转规律有水平翻转、垂直翻转等。
7. 图形平移规律图形平移规律是指在一组图形中,图形的平移方向和距离所遵循的规律。
常见的图形平移规律有水平平移、垂直平移等。
8. 图形缩放规律图形缩放规律是指在一组图形中,图形的缩放比例所遵循的规律。
常见的图形缩放规律有放大、缩小等。
9. 图形填充规律图形填充规律是指在一组图形中,图形的填充方式和颜色所遵循的规律。
常见的图形填充规律有交替填充、渐变填充等。
三、文字规律10. 文字替换规律文字替换规律是指在一组文字中,文字被替换成其他文字的规律。
常见的文字替换规律有字母替换、数字替换等。
文字排列规律是指在一组文字中,文字的排列顺序所遵循的规律。
常见的文字排列规律有逆序、顺序、交替等。
12. 文字组合规律文字组合规律是指在一组文字中,文字之间的组合所遵循的规律。
行测判断推理类比推理十大关系1.种属关系也称包含关系,是物种和所属的关系,是一个概念的外延包含并大于另一个概念外延范围,也可以认为是大类和小类的关系。
其逆向关系是包含于关系。
在类比推理应试中,要注意先后顺序的区别。
如老鼠和哺乳动物,老鼠的属是哺乳动物;再如教科书和书籍,教科书的外延包含于书籍的外延范围内。
2.分解关系(构成关系)分解关系是对合成事物拆分后构成的关系,即整体和部分的关系。
如:“汽车”与“汽车轮胎”、“国家”与“城市”等,在上述两个例子中,汽车和汽车轮胎之间是分解关系,因为相对于汽车轮胎来说汽车是一个整体,而汽车轮胎只是汽车这个整体的一部分,所以构成了整体和部分的分解关系;反之,汽车轮胎和汽车之间就是构成关系,因为汽车轮胎这个部分在前,而汽车这个整体在后。
我们也可以把这种关系进一步引申为组成关系、原料与产品的关系,如粘土∶瓷器,石灰石∶石灰膏等。
3.并列关系(同义、近义、同类)这里的并列关系是指逻辑反对关系。
概括地说,并列关系可分为同级并列和非同级并列。
同级并列的两个概念的临近属概念相同,如∶“冰箱∶电视”,它们的临近属概念都是“家用电器”。
与“计算机∶菜刀”比较,前者是同级并列,后者则是非同级并列,要参照具体语言环境分析断定。
试题中,通常考查同级并列关系。
但是,在选项中,会出现非同级并列概念的干扰,注意区分。
而同一关系则是进一步把这种并列关系的范围缩小了,但在关系上仍然可认为是并列的,如妈妈和母亲,大鲵与娃娃鱼。
因此,通常清况下我们把同义、近义、同类、同一等等关系都归为并列关系,也就是它们在同一个所属下是两个同级的种。
严格说来矛盾关系也应看作一种并列关系,但是为了做题和讲解的特殊需要,我们把矛盾关系单列讲解。
4.矛盾关系(相对关系)这种关系应该属于并列关系的一个很特殊的类,在各类试题中经常遇到,所以我们有必要重点讲解一下。
所谓矛盾关系,就是我们所说的对立关系,也就是在同一个所属下的两类事物或者词语的相对或相反关系。
数字推理十大题型秒杀技巧
1. 数字推理里的等差数列题型,那简直就是送分题呀!比如说1,3,5,7,这不是很明显的等差数列嘛,公差为2,下一个数不就是9 嘛!
2. 等比数列题型,哇塞,一旦发现规律就超简单的!像2,4,8,16,这倍数关系多明显呀,下一个肯定是 32 啦!
3. 平方数列题型,这可得瞪大眼睛找呀!像 1,4,9,16,不就是平方数嘛,下一个就是 25 咯!
4. 立方数列题型,这个有点难度哦,但找到了就很有成就感呀!比如1,8,27,64,那下一个就是 125 呀!
5. 组合数列题型,就像玩拼图一样有趣呢!比如奇数项和偶数项各有规律,找到就轻松解题啦!
6. 数字拆分题型,把数字拆开来分析,哎呀,真的很有意思!像34 可以拆成 3 和 4 嘛,然后再找规律。
7. 分数数列题型,这可不能被分数吓到呀!比如1/2,2/3,3/4,那下一个不就是 4/5 嘛!
8. 根式数列题型,虽然看着有点复杂,但找到了根号里的规律就迎刃而解啦!
9. 周期数列题型,就像循环播放的音乐一样有规律呀!比如1,2,
3,1,2,3,那下一个当然还是 1 啦!
10. 递推数列题型,一环扣一环的,多有意思呀!像前面两个数相加等于后面一个数,找到这个关系就好办啦!
我觉得呀,掌握了这些数字推理的秒杀技巧,就像是拥有了一把打开数字世界大门的钥匙,能让我们在数字的海洋里畅游无阻!。
公务员行测答题技巧:图形推理的十大规律【2】例题1答案: B解析:本题目考察的是图形的种类。
每一行都有3种不同的图形。
例题2七. (或者求异去同)例题1答案:A分析:所有图形的共同特点是都有三角形。
该题目考察的角度是求同。
即寻找所有图形的共同点。
八. 权重问题九. 图形的拆拼组合。
十. 图形的重心位置。
图形推理注意事项。
1. 有时候曲线看作边,有时候不看作边。
一般在国考中,边通常是指的直线边,而曲线不当作边。
例如:2007年国考真题:答案:D分析:该题目考察角度的是图形边数关系。
第一行三个图形边数与第二行三个图形边数对应相加等于第三行对应三个图形的边数。
本题曲线不算边。
考题中,解答有的题目我们需要把曲线也看成边。
这与命题专家的喜好有关。
根据具体题目,灵活处理。
在有的省考中,曲线和直线一样被看作一条边。
例如:2006年江苏省考真题:答案:C分析:本题考察角度是图形边数关系。
第一组图形,图形的边数和图形里面的小图案数量相等。
第二组图形,图形的边数比图形里面的小图案数量多1.本题中,圆圈被看作一条边。
2006年江苏省考真题:答案:B分析:本题考察角度是边的关系。
几个图形中,依次有1,2,3,4,5,6条边边长相等。
本题中,圆圈当作一条边。
这个题目本来有难度的,但是答案选项的设置不是很好,很多考生直接选B。
因为后面几个图形不就是三角形,四边形,五边形,六边形。
虽然这个思路是错误的,但同样得到了答案。
本题没有起到考察的作用。
2.一些图形可以当作立体图形,也可以当作平面图形。
例如:这个图形可以看作是立方体,也可以看作是平面图形六边形。
当作平面图形看待的时候,该图形的封闭部分有3部分。
该图形共有9条边。
2006年江苏省考真题:选出和所给图形规律不同的选项。
答案:A两种分析得到同样的答案。
分析一:上面5个图形的边数分别是2,5,1,4,3。
整理一下顺序,就是1,2,3,4,5。
下面4个图形的边数分别是12,6,8,7。
图形推理的十大规律一套图形专项突破中绝大多数例题都是公考真题,命题规范,指导性明确,具有很高的价值。
图形专项突破编写系统,几乎含盖图形推理全部类型的题目。
图形推理的两大灵魂是数量关系和图形的转动。
牢牢把握住这两大灵魂就基本把握了图形推理题目。
在这两大灵魂统帅下的十大基本规律,是每个想要在公考中取得优异成绩的考生必须系统熟练把握的。
图形推理的两大灵魂:数量关系和图形的转动。
这里以2007年国家公务员考试真题为例子来说明图形推理的两大灵魂。
1.答案:B分析:方法一,从图形旋转的角度来分析这个题目。
顺时针方向看,会发现黑色小方框在作顺时针旋转。
具体的说,第一行三个图形中,黑色小方框在作顺时针旋转;然后从第三列往下看,发现黑色小方框仍然在作顺时针旋转。
整个观察顺序是:第一行,从左向右,到了第三个图形,从上往下;到了右下角的图形,从右往左,到了左下角,再从下往上。
如果选择逆时针方向分析,会发现黑色小方框在作逆时针旋转。
最后同样得到答案B。
方法二,从图形的数量关系来分析这个题目。
图中含有黑色小方框的图形是成对出现的。
因此答案为B。
2.答案:A分析: 第一列,从下往上,三个图形中,图形外的线段数量分别是1,3,5。
第二列,从上往下,三个图形中,图形外的线段数量分别是7,9,1 1。
第三列,从下往上,三个图形中,图形外的线段数量分别是13,15,17。
从列的角度来考察的。
分析这类题目的时候,如果从行的角度去考察,难以发现规律,不妨改变一下角度,从列的角度去考察。
本题每个图形出头线段数目如下图:3.答案:D分析: 这个题目看从什么角度来分析。
如果把第一行三个小图形放在一起分析,然后把第二行三个图形放在一起分析,就很难找到正确的答案来。
如果把第一列的三个图形放在一起分析,把第二列的三个图形放在一起分析,就比较容易找出答案来。
整个题目的规律是:从列方向上来看,第一个图形的直线边数等于下面两个图形的边数之和。
以前考试的题目和参考书上的练习题目大多是从行的方向来考察的,这次考题换了一个角度。