李雅普诺夫第二法
- 格式:ppt
- 大小:450.00 KB
- 文档页数:19

李雅普诺夫第一方法和第二方法刘慈欣是中国著名的科学小说家。
他的作品《三体》引起了中外读者的热烈讨论。
他的作品也越来越深入人心并受到广泛的认可。
2012年,他凭借作品《三体》荣获第五届中国科幻小说银奖。
以刘慈欣名义,俄罗斯分析学家李雅普诺夫为预测未来事件制定了两种方法:第一种是李雅普诺夫第一方法,也被称为“加法法则”,它的基本思想是:以当前的社会形势为基础,根据以往的发展经验以及客观情况的变化,分析未来可能出现的新的社会现象和潮流,并预测未来可能出现的情况;第二种方法叫做“乘法法则”,该方法强调以社会时代和社会结构为基础,根据社会形势和社会变迁为基础,把具体的历史背景和文化氛围紧密结合起来,从总体上认识和理解未来可能出现的事件或现象。
1. 李雅普诺夫第一方法:加法法则第一种方法是李雅普诺夫第一方法,也被称为“加法法则”,它的基本思想是:以当前的社会形势为基础,根据以往的发展经验以及客观情况的变化,分析未来可能出现的新的社会现象和潮流,并预测未来可能出现的情况。
李雅普诺夫加法法则认为,当前也许存在各种模糊不清的社会现象,将其加以分析、剖析,深入了解它们的特性和内涵,再去看它们是否会影响未来,经过精心筛选、综合考量之后,利用科学的手段来预测未来可能发生的一些新的社会概念。
2. 李雅普诺夫第二方法:乘法法则第二种方法叫做“乘法法则”,该方法强调以社会时代和社会结构为基础,根据社会形势和社会变迁为基础,把具体的历史背景和文化氛围紧密结合起来,从总体上认识和理解未来可能出现的事件或现象。
李雅普诺夫乘法法则认为,在社会发展的历史进程中,人类的实际行为会受到多种因素的影响,必须从过去对社会发展的分析中总结出不同的历史规律,从而建立一个社会新状态,并能够准确预测未来的变化情况。








c et c y前页返回2 2c aet c y()xV&22xμ−=返回前页求出系统的李雅普诺夫第二法的基本思想ce tcy 1x 返回前页定理3渐近稳定cae tcy ()00≠=但x V&返回前页定理3⎪⎩⎪⎨⎧−−==21221x m x m k x x xμ&&⎥⎦⎤⎢⎣⎡=00e x 渐近稳定et c y返回前页1 xca e tcy ⎪⎩⎪⎨⎧−==1221x m k x x x &&⎥⎦⎤⎢⎣⎡=00e x 返回前页定理4李雅普诺夫意义下稳定cet c y1x返回前页定理3不稳定ca e tcy ()00≡=但x V&返回前页定理3⎪⎩⎪⎨⎧+−==21221x m x m k x x x μ&&⎥⎦⎤⎢⎣⎡=00e x 不稳定状态平面图状态仿真曲线注意tcy 前页返回前图?李氏函数选择不当!cet c y返回前页定理3et c y返回前页e虚构atcae tcy ()=V x ()02221>+=x x V x ()0 ≡x V &()0222≤−=x V x &ec ayt c etcy 返回前页定理4cae tcy ⎥⎦⎤⎢⎣⎡=0n πe x ⎪⎩⎪⎨⎧−== x L gx x x1221sin &&状态仿真曲线李雅普诺夫意义下稳定返回前页tcy 0≡返回前页定理3cae tcy 状态平面图状态仿真曲线()00≡=但x V&⎪⎩⎪⎨⎧−== x L g x x x1221sin &&2Dx −()L ,,,nn πe 2100±±=⎥⎦⎤⎢⎣⎡=x 垂直向下渐近稳定前页返回cae tcy 相平面图θL。

第讲李雅普诺夫第二方法李雅普诺夫第二方法是一种用于研究动力系统稳定性的数学方法。
它是通过构造一个李雅普普新函数来分析和确定系统的稳定性。
在动力系统中,一个常见的问题是研究系统在长时间演化之后是否会收敛到一个稳定的状态。
稳定性是指系统对初始条件变化的敏感程度,如果系统在不同的初始条件下产生相似的行为,那么就可以认为该系统是稳定的。
李雅普诺夫第二方法基于一个基本原理,即系统中存在一个李雅普诺夫函数,该函数随着时间的增加而递减。
这个函数被称为李雅普诺夫函数,它用来衡量系统的稳定性。
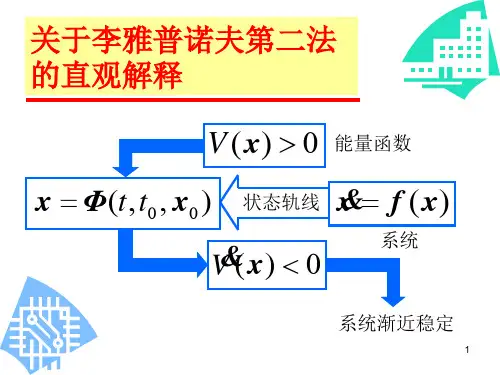
李雅普诺夫第二方法的核心思想是构造一个李雅普诺夫函数,并利用该函数来证明系统的稳定性。
具体步骤如下:1. 假设动力系统的状态方程为dx/dt = f(x),其中x是系统的状态向量,f(x)是系统的演化函数。
2.选择一个李雅普诺夫函数V(x),它必须满足以下条件:a.V(x)连续可微;b.V(x)>0,当且仅当x=0时取等号;c.V(x)在整个状态空间上是正定的。
李雅普诺夫函数V(x)的选择是一个关键问题,通常需要根据具体问题的特点来确定。
常见的李雅普诺夫函数有能量函数、距离函数等。
3. 计算李雅普诺夫函数V(x)对时间的导数dV/dt,利用系统的状态方程进行替换,即dV/dt = (∂V/∂x)·f(x)。
4. 判断dV/dt的正负性,如果dV/dt恒为负(或恒为正),则说明系统的稳定性得到证明。
如果dV/dt既有正值又有负值,那么不能断定系统的稳定性,可能需要使用其他方法来进行进一步的分析。
李雅普诺夫第二方法的优点是在一定条件下,可以通过构造李雅普诺夫函数来判断系统的稳定性。
这种方法经过了长期的发展和完善,在许多实际问题中得到了成功的应用。
需要注意的是,李雅普诺夫第二方法仅适用于连续系统和微分方程,对于离散系统和差分方程并不适用。
此外,选择合适的李雅普诺夫函数是一个关键问题,不同的李雅普诺夫函数可能导致不同的稳定性结论。