第三章 条件概率与条件期望

概率论中的条件概率公式详解贝叶斯定理条件期望等概率论是数学中的一门重要学科，研究的是随机事件的概率性质以及它们之间的关系。

条件概率公式、贝叶斯定理和条件期望是概率论中的重要概念和定理，它们在解决实际问题中具有广泛应用。

本文将对这些概念进行详细解释和讨论。

一、条件概率公式条件概率是指在已知某一事件发生的条件下，其他事件发生的概率。

设A和B是两个事件，且P(B)≠0，那么在事件B已经发生的条件下，事件A发生的概率记作P(A|B)，读作“A在B发生的条件下发生”。

条件概率公式的形式为：P(A|B) = P(AB) / P(B)其中，P(AB)表示事件A和B同时发生的概率，又称为A与B的交集的概率。

通过这个公式，我们可以根据已知的条件概率来计算其他事件的概率。

二、贝叶斯定理贝叶斯定理是概率论中的核心定理之一，它描述了在已知某一事件发生的条件下，其他事件发生的概率如何更新。

设A和B是两个事件，且P(A)≠0，P(B)≠0，那么贝叶斯定理的表达式为：P(B|A) = P(A|B) * P(B) / P(A)其中，P(B|A)表示在事件A已经发生的条件下，事件B发生的概率。

贝叶斯定理的主要应用在于通过已知的先验概率和条件概率来计算后验概率。

它在统计学、生物信息学、机器学习等领域有着广泛的应用。

三、条件期望条件期望是在已知某一事件发生的条件下，随机变量的期望值。

设X和Y是两个随机变量，且P(Y=y)≠0，那么在事件Y=y已经发生的条件下，随机变量X的条件期望记作E(X|Y=y)。

条件期望的计算公式为：E(X|Y=y) = Σx(x * P(X=x|Y=y))其中，Σ表示对所有可能的取值进行求和。

通过条件期望，我们可以得到在给定条件下随机变量的平均值，从而更好地理解和分析随机事件的分布特性。

综上所述，条件概率公式、贝叶斯定理和条件期望是概率论中的重要概念和定理。

它们可以帮助我们计算和预测事件的概率，以及根据已知条件更新概率。

一、条件概率生活中很多概率都是在某些特殊条件下的概率。

比如你想知道你在家感染新冠的概率，这是取决于很多方面的，比如，政策有没有放开、是否位于高风险区等等。

只有在这些条件的限制下，我们才能较为准确的求出你想知道的概率。

基本概念：设A，B是随机试验E的两个随机试验，且P(B)>0，称P(A|B)=\frac{P(AB)}{P(B)} 为在事件B发生的条件下，事件A发生的条件概率。

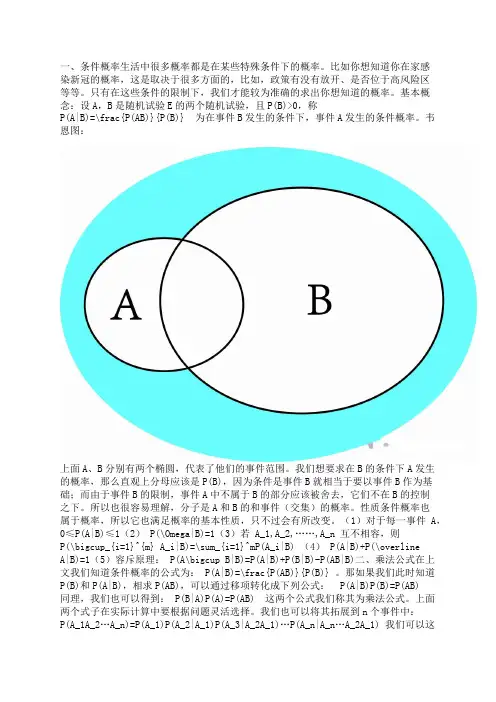
韦恩图：上面A、B分别有两个椭圆，代表了他们的事件范围。

我们想要求在B的条件下A发生的概率，那么直观上分母应该是P(B)，因为条件是事件B就相当于要以事件B作为基础；而由于事件B的限制，事件A中不属于B的部分应该被舍去，它们不在B的控制之下。

所以也很容易理解，分子是A和B的和事件（交集）的概率。

性质条件概率也属于概率，所以它也满足概率的基本性质，只不过会有所改变。

（1）对于每一事件A，0≤P(A|B)≤1（2） P(\Omega|B)=1（3）若A_1,A_2,……,A_n 互不相容，则P(\bigcup_{i=1}^{m} A_i|B)=\sum_{i=1}^mP(A_i|B) （4） P(A|B)+P(\overlineA|B)=1（5）容斥原理： P(A\bigcup B|B)=P(A|B)+P(B|B)-P(AB|B)二、乘法公式在上文我们知道条件概率的公式为： P(A|B)=\frac{P(AB)}{P(B)} 。

那如果我们此时知道P(B)和P(A|B)，相求P(AB)，可以通过移项转化成下列公式： P(A|B)P(B)=P(AB)同理，我们也可以得到： P(B|A)P(A)=P(AB) 这两个公式我们称其为乘法公式。

上面两个式子在实际计算中要根据问题灵活选择。

我们也可以将其拓展到n个事件中：P(A_1A_2…A_n)=P(A_1)P(A_2|A_1)P(A_3|A_2A_1)…P(A_n|A_n…A_2A_1) 我们可以这样理解：$P(A_1)$是假设A1正确，$P(A_2|A_1)$是假设A1正确的情况下A2正确，以此类推三、全概率公式有限划分基本概念：设 \Omega 为随机试验E的样本空间，B1，B2 ，…，Bn为E的一组事件，若(1) Bi∩Bj =f ,i ≠ j(2) B_1∪B_2 ∪…∪B_n=\Omega则称B1，B2，…，Bn 为 \emptyset 的一个有限划分，或称完备事件组。

条件期望和条件概率的关系条件概率直接决定条件期望的大小。

设X,Y是两个离散的随机变量，X可能的取值是x1,x2,...,xm；Y可能的取值是y1,y2,...,yn。

那么如果已经知道X,Y的联合概率分布，即知道：Pr(X=xi,Y=yj)是多少的话（Pr（A）是说A的概率，i=1,2,...,m;j=1,2,..,n，此表达式的含义就是随机变量X取第i个结果，同时Y取第j个结果的概率），那么X,Y的条件概率就可以表达为：Pr(X=xi|Y=Yj)（含义是给定随机变量Y取第j个数，在这种情况下X取第i个数的概率，竖线右边的事件是条件事件），它等于Pr(X=xi,Y=yj)/Pr(Y=Yj)。

此时，在给定Y=Yj这一条件下，X的条件期望是：E(X|Y=Yj)=Sum(i 从1到m){xi*Pr(X=xi|Y=Yj)}(Sum是求和)。

所以，条件期望和条件概率的关系就和普通的期望-概率关系一样，知道条件概率分布就可以求条件期望，但是反过来不可以。

如果X是连续型随机变量，那么求和符号要变成定积分，但其原理还是和上面一样的。

注意任何条件期望的计算都必须讲清楚条件，不给条件求条件期望是不可能的。

有时候我们把E(X|Y=y)简写为E(X|Y)，但是这只是为了方便。

要求条件期望，必须知道条件分布，求条件分布的公式，在离散情况下就是Pr(X=xi,Y=yj)/Pr(Y=Yj)，连续情况下另有公式，为{偏导数F(x,y)对y/f(y)}。

F(x,y)为X和Y的联合分布函数，f(y)为Y的分布密度函数。

你如果需要知道这个再问。

另外，条件事件不一定是Y=y，也可以是任何关于随机变量Y的函数方程，比如：E(X|Y^2<=4)，这就是说，给定Y的取值范围是（-2,2），求X的平均值。

此时就需要用到二重积分，因为Y的取值已经是一个区间了，合上X可能取值的范围，就组成了一个平面区域，所以要对x,y的联合分布密度函数f(x,y)二重积分来计算。

条件期望与条件分布我们已经学习了条件概率的基本概念和性质，但只局限于讨论以事件(集合)为条件的情形。

事件作为条件，意味着先验知识的加入导致了样本空间的变化，从而影响概率计算。

由于随机变量是概率论研究的核心内容，很自然地需要将“条件”的概念和方法拓展到随机变量中来。

特别地，条件概率刻画了样本空间中不同集合在概率计算中的相互影响，容易由此联想到“条件”在研究随机向量的各分量间相互关联以及随机过程中所具有的价值。

所以，本章引入条件期望和条件分布的概念，并讨论其性质和应用，让读者体会“条件”对于研究随机变量间关联的重要意义，明确基本概念，掌握与之相关的基本计算方法。

PART A条件期望我们用一个简单例子作为引入。

设离散随机变量X和Y，X取值于{x1,···,x n}，Y取值于{y1,···,y m}。

考虑事件{Y=y k}，在其条件下，X的概率分布会发生变化，P({X=x i}|{Y=y k})=P({X=x i}∩{Y=y k})P({Y=y k}),通常称该概率分布为条件分布，记作P(X=x i|Y=y k)=P(X=x i,Y=y k)P(Y=y k),(1-1)这个概率中包含了Y所提供的先验信息，并将该信息带入到了期望的计算中。

E(X|Y=y k)=n∑i=1x n P(X=x i|Y=y k),(1-2)称该期望为条件期望。

条件期望给出了在已知某些先验信息的条件下，随机变量X取值的平均水平。

上述讨论对于离散随机变量比较准确，但是推广到连续情形会遇到本质的问题。

如果Y是连续随机变量，则P(Y=y)=0，(1-1)没有明确的含义。

如何克服这一困难呢？现代概率论中关于条件期望的阐述为我们提供了帮助。

基本概念首先，明确一个基本事实，条件期望是随机变量，不同于普通期望是确定性常数。

事实上，条件期望的取值取决于随机变量Y，并由此依赖于样本空间。

具体地说，设概率空间为(Ω,F,P)，如果Z(ω)=E(X|Y=Y(ω)),ω∈Ω,(1-3)则有Y(ω)=y k=⇒Z(ω)=E(X|Y=y k),为方便，记Z(ω)为E(X|Y)(ω)。