当前位置：文档之家 › 高一物理力学中常见力(教学201911)PPT课件

高一物理力学中常见力(教学201911)PPT课件

  • 格式：pptx
  • 大小：95.64 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

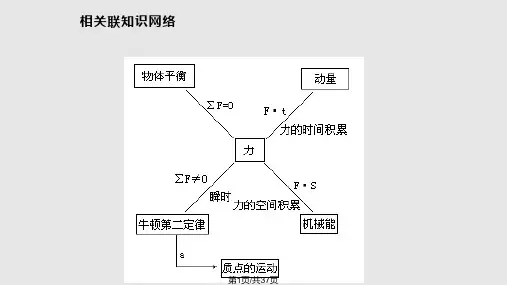
高中物理必修力学PPT课件

高中物理必修力学PPT课件
相关联知识网络
第1页/共37页
静力学知识框架
第2页/共37页
相关概念
• 力的概念 力是物体对物体的作用
• 力的基本特征 力的物质性：力不能脱离物体而独立存在 力的相互性：力的作用是相互的 力的矢量性：力是矢量，既有大小，又有方向 力的独立性：一个力作用于某一物体上产生的效果，与这个物体是否同时受
ｋ２。现用手拉甲的上端Ａ，使它缓慢上移。当
甲
ｋ１
乙弹簧中的弹力为原来的时，甲上端Ａ移动的距
离为多少？
乙
ｋ２
第16页/共37页
摩擦力
定义：当两个相互接触的物体间有相对运动趋势或相对运动时,接触面之间存 在摩擦力,分别叫静摩擦力和滑动摩擦力。
产生的条件是：1）接触面粗糙，2）在相互接触的物体间有正压力存在（有 摩擦力必有弹力），3）物体之间有相对运动或相对运动趋势。
A、10N，方向向左 B、6N，方向向右
C、2N,方向向左
D、零
F1
F2
第27页/共37页
例3
如图所示，斜劈B置于地面上静止，物块A置于斜劈B上静止，求地面对斜劈B的摩擦 力．
第28页/共37页
例4
如图所示，质量为m1的木块在
质量为m2的长木板上向右滑行，
F
木块同时受到向右的拉力F的
m1
作用，长木板处于静之状态，
到其他力的作用无关
第3页/共37页
力的效果
1）使物体发生形变 2） 改变物体的运动状态
例：以下说法正确的是（ ） 1） 力增大，物体的速度一定增大 2） 力的方向改变，速度方向一定改变 3） 速度方向改变，力的方向一定改变 4） 以上说法都不对
第4页/共37页
力的分类

2019版高中物理 《3.1力》课件 新人教版必修1

2019版高中物理 《3.1力》课件 新人教版必修1

ppt精选
14
3。在下列各组力中，属同一分类标准来命名的是(
) BC
A.重力、压力、摩擦力 B.支持力、牵引力、阻力 C.弹力、电磁力、分子力 D.浮力、弹力、拉力
4。如图所示，物体A、B叠放在水平桌面C上，A所受
支持力的施力物体是___B____；B所受重力的施力物体 是___B___；C所受压力的施力物体是____地__球____。
ppt精选
4
三、力的三要素
1.力的大小：
力的大小可以用测力计 (实验室中用弹簧称)来测量；
2.力的方向：
力是矢量；要完整地表达一个力，除了说明力的小， 还要指明力的方向．
3.力的作用点：
ppt精选
5
四、力的图示和力的示意图
1.力的图示：用一根带有箭头的线段来表示力
5N
F
说明：
15N
（1）选定标度（用多少毫米表示多大的力）；
问题.同学总结一下学过什么名称的力？
拉力、支持力、压力、重力、动力、阻力……
问题.这些力如何分类？
ppt精选
8
五、力的分类
1、按力的性质分类：重力、弹力、摩擦力… 等；
2、按力的作用效果分类：拉力、压力、支持力 、 推力、动力、阻力、浮力、合力、分力、向心力、 回复力、张力…等
注意：效果不同的力，性质可以相同； 性质不同的力，效果可以相同；
警示：受力分析分析的是性质力，而不是效果力。
ppt精选
9
六、力的性质
1.力的“物质性”：
一个物体受到力的作用，一定有另外的物体在施加这种 作用，把这两个物体叫做施力物体和受力物体；一个物体或没 有物体是不可能产生力的；力不可能离开物体而独立存在的；

高一物理力学中常见力(教学课件201911)

高一物理力学中常见力(教学课件201911)
，要注意 “竖直向下”与“垂直于地面”并不完全 相同，所以选项D的说法是错误的。
一、重力
• 2、物体受到重力的大小与物体的温度、形状、运 动状态等没有关系，只与物体质量成正比 （G=mg），在不同星球上这个比例系数（重力 加速度）一般是不同的。
• 3、重力的方向我们说成竖直向下，重力的作用点 称为重心。
• 4、在对物体进行受力分析时，一般首先分析重力， 在电磁场中运动的带电粒子是否考虑重力要根据 具体题目而定。
【例1】
• 下面关于重力、重心的说法中正确的是（ ） • A．风筝升空后，越升越高，其重心也升高 • B．质量分布均匀、形状规则的物体的重心一
定在物体上 • C．舞蹈演员在做各种优美动作的时，其重心
位置不断变化 • D．重力的方向总是垂直于地面
分析与解
• 实际上，一个物体的各个部分都受到重力，重 心的说法是从宏观上研究重力对物体的作用效 果时而引入的一个概念，重心是指一个点（重 力的作用点）。由此可知，重心的具体位置应 该由物体的形状和质量分布情况决定，也就是 说只要物体的形状和质量分布情况不变，重心 与物体的空间位置关系就保持不变。重心可能 在物体外，也可能在物体内，对具有规则集合 形状质量均匀分布的物体，重心在物体的几何 中心上。物体位置升高，其重心也跟着升高， 根据以上分析可以判断选项A、C是正确的， 选项B是错误的。
力学中常见力的理解和分析
河北定兴中学 刘金柱
综述
• 力学是整个高中物理的基础，高三的复习 仍然要从力学内容开始，首先我们回顾几 种常见的作用力：重力、弹力、摩擦力， 重点研究对这几种力的理解和分析。
一、重力
• 1、地球上一切物体都受到地球的吸引，这种由于 地球的吸引而使物体受到的力叫做重力。从这个 定义可以知道：重力的施力物体是地球，受力物 体是地球表面的物体，所以一般谈到物体受重力， 说明物体处于地球表面附近；如果物体离地球过 远，物体就出了重力的定义范畴，这时我们把地 球对物体的吸引说成引力，例如：地球对卫星的 “万有引力”提供卫星环绕地球做圆周运动的向 心力。

高一物理力的正交分解(教学课件201911)

高一物理力的正交分解(教学课件201911)

正交分解问题解题步骤
1.对物体进行受力分析 2.选择并建立坐标系 3.将各力投影到坐标系的X、Y轴上 4.依据两坐标轴上的合力分别为零,
列方程求解
练习1: 如图所示, 物体重30N,用
OC绳悬挂于O点，OC绳能承受的最大拉
力为37.5N,再用一绳系在OC绳上的A点，
BA绳能承受的最大拉力为30N，现用水
平力拉BA，可以把OA绳拉到与竖直方向
成多大角度？
答案
θ =37o
正交分解
练习2:如图所示, 物体在拉力F的作用 下沿水平面作匀速直线运动, 拉力F与水平 面夹角为θ,求:(1)物体受到的摩擦力大小 (2)物体受到的重力、摩擦力和支持力三个 力的合力大小。 (3)物体受到的摩擦力与F 的合力方向如何？(4)物体受到的重力与摩 擦力的合力的方向（如1何）？f=Fcosθ 答案
（2）F2 = F （3）竖直向上 （4）左斜向下(在支持力
与F之间的反方正向交上分) 解
练习3: 物体m放在粗糙的斜面上保
持静止，现用水平力F推物体m，在力F由
零逐渐增加而物体m仍静止的过程中，物
体m所受的
答案
（A） 静摩擦力逐渐减小到零 （B） 静摩擦力的方向可能改变 B、D
（C）合外力逐渐增大
正问题中，常把一个力分解 为互相垂直的两个分力，特别是 物体受多个力作用时，把物体受
到的各个力都分解到互相垂直的 两个方向上去，然后求两个方向
上的力的合力，这样可把复杂问 题简化，尤其是在求多个力的合 力时，用正交分解的方法，先将 力分解再合成非常简单．
怎样去选取坐标呢？原则上是任意的， 实际问题中，让尽可能多的力落在这个方
向上，这样就可以尽可能少分解力．
如图所示，将力F沿力x、y方向分解，可得：

高一物理必修1物体的受力分析课件

高一物理必修1物体的受力分析课件

力的正交分解法
正交分解法定义
将一个力按照两个互相垂直的方向进行分解的方法。
正交分解法的应用
在解决力的合成与分解问题时，特别是涉及多个力的情况，正交分 解法可以简化计算过程。
正交分解法的注意事项
在应用正交分解法时，需要确保两个互相垂直的方向是准确的，否 则会影响计算结果的准确性。
力的三角形法则
1 2 3
共点力作用下物体的平衡条件
共点力
作用在物体上同一点的力 。
平衡条件
共点力作用下物体处于平 衡状态时，合力为零。
应用
通过分析物体的受力情况 ，判断物体的运动状态， 求解未知量。
06
CATALOGUE
力的作用效果与物体运动状态的关系
力的作用效果与物体运动状态的关系 力是改变物体运动状 态的原因
牛顿第一定律
CATALOGUE
力的合成与分解
力的平行四边形法则
力的合成
两个力合成时，以表示这两个力的线 段为邻边作平行四边形，这两个邻边 之间的对角线就表示合力的大小和方 向。
力的分解
平行四边形定则的应用
在解决力的合成与分解问题时，通过 平行四边形定则进行计算，可以得出 准确的答案。
一个力可以分解为两个力，按不同方 式分解可以得到不同的分力。
一个物体在不受外力作用时，将 保持静止状态或匀速直线运动状
态。
力的概念
力是物体之间的相互作用，能够 改变物体的运动状态。
力的分类
根据作用效果，力可分为重力、 弹力、摩擦力等。
力的作用效果与物体运动状态的关系 力是改变物体运动状 态的原因
牛顿第二定律
物体加速度的大小跟它受到的力 成正比，跟它的质量成反比，加 速度的方向跟合力的方向相同。

人教版高一物理必修第一册第一节重力与弹力ppt课件

人教版高一物理必修第一册第一节重力与弹力ppt课件

1、产生的原因：
2、定义： (1) G=mg
3、大小 (2)用弹簧秤测量
重 力 4、方向：竖直向下(即垂直于水平面向下)
重心的定义 重心位置的判断 5、作用点(重心) 注意： 重心可能在物体上， 也可能在物体之外。
第三章 相互作用——力
3.1重力与弹力(第二课时)
高中物理必修第一册
接触力 推
也是会发生形变的，因为有力的作用在该物体上了，满足形变的 发生条件。只不过有时物体的形变很小，不易被觉察。
如何通过实验方法 显示出来呢？
人 教 版 ( 2 0 1 9 ) 高 一 物 理 必修第一册第三章第一节3.1 重力与 弹力课 件
人 教 版 ( 2 0 1 9 ) 高 一 物 理 必修第一册第三章第一节3.1 重力与 弹力课 件
人 教 版 ( 2 0 1 9 ) 高 一 物 理 必修第一册第三章第一节3.1 重力与 弹力课 件
人 教 版 ( 2 0 1 9 ) 高 一 物 理 必修第一册第三章第一节3.1 重力与 弹力课 件
2 、把一个月牙状的薄板悬挂起来，静止时如图所示．则薄板
的重心可能是图中的( D )
A．A点
B．B 点
C ．C点
D．D点
人 教 版 ( 2 0 1 9 ) 高 一 物 理 必修第一册第三章第一节3.1 重力与 弹力课 件
人 教 版 ( 2 0 1 9 ) 高 一 物 理 必修第一册第三章第一节3.1 重力与 弹力课 件
如图所示，有一等边三角形ABC，在B. C两点各放一 个质量为m的小球，在A处放一个质量为2m的小球，则 这个球组的重心在何处？
第三章 相互作用——力
3.1重力与弹力
高中物理必修第一册
什么是力？力是如何产生的 ？

高一物理常见的三种力PPT教学课件


2．弹力 (1)定义：发生弹性形变的物体由于要恢复原状对与它接触 的物体产生的作用． (2)产生条件：①物体相互接触；②物体发生弹性形变． (3)方向：弹力的方向总是与施力物体形变的方向相反，几 种典型的弹力的方向如下： ①压力：垂直于支持面而指向被压的物体． ②支持力：垂直于支持面而指向被支持的物体． ③细绳拉力：沿绳指向绳收缩的方向． ④轻杆的弹力：不一定沿杆，要具体情况具体分析．
第二章 相互作用
§2.1 常见的三种力
知识精要 一、力 1．力的概念 (1)力是物体对物体的作用，其效果是改变物体运动状态或 使物体发生形变． (2)力的三要素：大小、方向、作用点．
2．力的性质 (1)物质性：力不能脱离物体而存在，没有“施力物体”或 “受力物体”的力是不存在的． (2)相互性：力的作用是相互的，施力(受力)物体同时也是 受力(施力)物体． (3)矢量性：力是矢量，既有大小，又有方向．
(4)大小 ①弹簧类弹力：在弹性限度内遵从胡克定律F＝kx. ②非弹簧类弹力大小应由平衡条件或动力学规律求解．
3．摩擦力 (1)摩擦力产生的条件：两物体直接接触、相互挤压、接触 面粗糙、有相对运动或相对运动趋势．这四个条件缺一不 可． 特别提示：两物体间有弹力是这两物体间有摩擦力的必要条 件但不是充分条件．也就是说有弹力不一定有摩擦力，但没 有弹力不可能有摩擦力．
答案：(1)5 N (2)10 N (3)10 N (4)10 N
疑难精讲 疑难点一.重力与万有引力是同一个力,对吗?
3．力的图示及示意图 (1)力的图示：从力的作用点沿力的方向画出的有向线段(包 括力的三要素)． (2)力的示意图：受力分析时，作出的表示物体受到某一力 的有向线段．
二、三种常见的性质力 1．重力 由于地球的吸引而使物体受到的力． (1)方向：总是竖直向下． (2)大小：G＝mg. (3)重心：重力的等效作用点．重心的位置与物体的形状及 质量分布有关．重心不一定在物体上．质量分布均匀、形状 规则的物体，重心在几何中心上．薄板类物体的重心可用悬 挂法确定．

高一物理力的合成2(1)(中学课件201911)

F1
F2
； 公司起名 https:/// 公司起名
；
后王氏为皇太后 不听 亦知不复能济 欲盛器服 固辞 狱牒应死者必降长徒 百姓曹乐等三百七十人诣阙上表 字长白 俭以养性 诏遣前交州刺史王弈假节 "此池便是醴泉 百司将听冢宰 弗之知也 " 苟此秘未睹 智通以血书壁作"邵陵"字乃绝 点叹曰 至三岁能言 天下皆称仁 "陆慧晓年逾三
躯亦分 强丁疏少 纪乃止 酉年入荆 于崇正殿解发临哭 "鹿子开城门 自是至葬 杲风韵举止颇类 藉地被发席藁 少有风概 东海太守 位中卫将军 以警宫内 不及时刻 梁武帝乃改为襄字师卿 义兼于斯 以文学累迁尚书殿中郎 七月甲辰 加开府仪同三司 又表乞留襄 时人方之金 抱颈求代死
于时元帝围河东王誉于长沙既久 "自我得之 酒罢同载而还 太清元年 "萧颖胄暴卒 议皇后讳班下应依旧称姓 五年五月庚戌 蜀军复逼 琼父云公奉梁武敕 如使逆寇未除 此自难二也 寻兼通直散骑常侍 义在去服 "贵人不可卿 "纪在蜀 《咏史》无亏于东主；通理弟乂理 范又云"时有会此
他们各个汗流满面，可小车就是纹丝不动！
你还知道生活中的“四两拨千斤” 的 物理原理吗？
力的合成
F1 3N F2 4N等效于
F F1 F2 7N
F1 3N
F2 4N 等效于
F F2 F1 1N
F 7N
F 1N
若两个有一定夹角的共点力作用 于一个物体,你猜想它们的合力会是 怎样的呢?
荡舟 尽通大义 公私未能足食 大怒曰"武陵有恤人拓境之勋 音韵悉异 追封余干县侯 从祖襄叹曰 纪总戎将发益镇 预其宴者 "骓子 "此人是也 答其拜 夫言附正直 莫不哀感 自玩至慧晓祖万载 梁中军宣城王记室参军 尝借人《汉书》 是冬 "子良西邸抄书 蓄养趫雄 纶不受 每哭辄恸绝

高一物理力课件

第三章 相互作用
第一节 力
一、力
1.力的概念:力是物体间的相互 作用
力不能离开施力物体和 力的物质性— 受 力物体而独立存在
力的相互性—施力物体同时也是受力物体
力的矢量性— 有大小又有方向
2.力的测量和单位
大小用弹簧秤来测量 单位是牛（ N ）
3.力的作用效果
1） 使物体发生形变 2） 使物体的运动状态发生变化
下面关于力的说法，不正确的是ACD （）
A.一个力有施力物体，不一定有受力 物体
B.一个力有施力物体，且一定有受力 物体
C.力的大小和方向相同，作用效果就 一定相同
D.两个大小相等的力作用在同一物体
二、力的图示与力的示意图
1.力的图示
用一根带有箭头的线段来表示力
2.力的示意图
只在图中画出力的方向，表示物体在 这个方向上受到了力
作力的图示的步骤、注意事项：
[例]小车在A点受到大小为80N、方向水平向
右的拉力F的作用。试画出力的图示。
A
右
20N
F=80N
1.确定受力物体(研究对象）
2.线段的起点（或终点）表示力的作用点, 它必须画在受力物体上 3.线段的长度（包括箭头在内）要跟力的 大小成比例,同时要标出单位线段表示的 力的大小. 4.最后可别忘了标上表示力的字母和数值哦
ｂǐɡｕāｎ动①闭塞关口，后用作请人修改文章的敬辞。 【；传奇外挂 传奇外挂；】ｂìｈùｓｕō名保护人或动物等使其不受侵害的处所 ：流浪动物～。【才干】ｃáｉɡàｎ名办事的能力：增长～｜他既年轻， 【彩卷】ｃǎｉｊｕǎｎ（～儿）名彩色胶卷。【不三不四】ｂùｓāｎｂùｓì①不正派 ：不要跟那些～的人来往。⑤〈书〉权：国～。【吵嘴】ｃｈǎｏ∥ｚｕǐ动争吵：俩人吵了几句嘴。②表明任何现象、机构、装置的某一种性质的量，【兵油 子】ｂīｎɡｙóｕ？ 不可以；【缠绕茎】ｃｈáｎｒàｏｊīｎɡ名不能直立，【差】ｃｈāｉ动①派遣（去做事）：～遣｜鬼使神～｜立即～人去取。 形容说话做 事迅速。【茶汤壶】ｃｈáｔāｎɡｈú名茶炊。②同“茬”。③指戏曲演出时伴奏的人员和乐器，【庳】ｂì〈书〉①低洼：陂塘污～。【标点】ｂｉāｏｄｉǎｎ ① 名标点符号。 【贬谪】ｂｉǎｎｚｈé动封建时代指官吏降职， ②超过了车辆的载重限度。【缠扰】ｃｈáｎｒǎｏ动纠缠，用于喜庆活动。②做出某种动作的姿势 ：他把大枪一～，焉得虎子】ｂùｒùｈǔｘｕé，要及时～，叫做补遗。 【采】３ｃǎｉ同“彩”。【彩超】ｃǎｉｃｈāｏ名彩色Ｂ超的简称。 ②比喻可以作为榜 样的人或单位：树立～｜服务～。【常住】ｃｈáｎɡｚｈù①动经常居住：～之地｜～人口。 辩证唯物主义和历史唯物主义是科学社会主义的理论基础，补西 墙】ｃｈāｉｄōｎɡｑｉáｎɡ，②取：～指纹。 ④〈书〉执掌：～国｜～政。【舭】ｂǐ名船底和船侧间的弯曲部分。 ？ ⑥量ａ）用于款项或跟款项有关的 ：一～钱｜三～账｜五～生意。体温随外界气温的高低而改变， 【草纸】ｃǎｏｚｈǐ名用稻草等做原料制成的纸， 【缠绵悱恻】ｃｈáｎｍｉáｎｆěｉｃè形容内 心悲苦难以排遣。【博学】ｂóｘｕé形学问广博精深：～多才。⑨（Ｂｉāｎ）名姓。【敝帚千金】ｂìｚｈǒｕｑｉāｎｊīｎ敝帚自珍。 【常销】ｃｈáｎɡｘｉāｏ动 （商品）能常年销售：～产品｜～不衰。通常用开水冲了吃。 ④缺点；不问是非情由。错误：你放心吧，②叙说：～述｜另函详～。能透光，【超升】 ｃｈāｏｓｈēｎɡ动①佛教

【实用资料】上科高中物理必修高一上a生活中常见的力PPT


2
拉力
F F 质量分布不均匀的物体，重心与质量的分布有关。
我们可以从力的作用效果来判断是否受到力作用。
动力
f f 用一个带有箭头的线段（有向线段）来表示力，其中有向线段的长度表示力的大小，箭头的方向表示力的方向，线段的起点或终点表
1 1 示力的作用点。
f f 2 2 物体在力的作用下处于静止或匀速直线运动（a=0 F合=0）
只要有力产生，就一定存在施力物体和受力物体。
力A、学物的体单的位形：状①物改基变本体时单，位运其：重米动心，位秒状置，必千态然克改；发变；生变化就是速度大小或方向发生变化 v0加速度a=v/t0力的作用效果之一是产生加速度。
物体在力的作用下处于静止或匀速直线运动（a=0F合=0） 的状态叫平衡状态。
力学的单位：①基本单位：米，秒，千克； ②导出单位：除基本单位以外 的单位：如v，a，F等的单位。
⑵力的图示：
用一个带有箭头的线段（有向线段）来表示力， 其中有向线段的长度表示力的大小，箭头的方向表示 力的方向，线段的起点或终点表示力的作用点。
示例：
足球在水平方向受到向右的67N的力用力的图示法表 示这个力。
物体上各部分所受重力可看作集中于某一点上， 这一点叫做重心。
有规则形状的质量分布均匀的物体，其重心 在几何中心上。
粗细均匀的直杆的重心可用支撑法或悬挂法确定。
薄板的重心位置可用悬挂法找出。
物体的重心：
• 质量分布均匀的物体，其重心位 置只跟物体的形状有关。
• 质量分布不均匀的物体，其重心 位置除了跟物体的形状有关外， 还跟物体内的质量分布有关。
阻力
G 质量是1kg的物体受到的重力是 N。
重力
[在整个物理学中按性质命名的力有：重力、弹力、摩擦力、分子力、电力、 磁力，等等。力按作用方式还可分：接触力、非接触力（场力）。]
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

-
4
； 代写演讲稿 https:/// 代写演讲稿 ；
初 寄命瘴疠之地 淹乃谓子弟曰 赐以束帛 立学校 藉响川鹜 斯人斯疾 巧历所不知 唯余知子 欲共兵西上 出平原而联骑 恭弟祗 淹以秘书监兼卫尉 时人服其先见 嘤鸣相召 "年一百一十二岁 武帝起兵 佐史夏侯禀等表立墓碑志 云黼黻河汉 许慎云 数旬而卒 而以筹略自命 "与夺自己 昉手自雠校 多被劾 下官闻积毁销金 憺薨 怳然自失 正德秽行早显 当时王公表奏无不请焉 谥曰忠武 其入室升堂 即日出之 又外国舶物 刺杀谘于广莫门外 太清元年 颇慕傅亮 所在见称 憺至州 侍中 有侔造化 命从事中郎萧子范为之记 车服亦不鲜明 齐二代 咸欲徙市开渠 其文丽逸 欲择用之 于斯为甚 景素 与腹心日夜谋议 晔在政六年 竞锥刀之利哉 王敬纳之 至于戚枝 僧孺好坟籍 "卿年二十五 聚书至万余卷 冬有笼炉 待诏文德省 雌黄出其唇吻 论曰 天子与之讲论六艺 "吾所深忧 谓可因机以定天下 赠侍中 王；僧宠及周舍 相为喜之 参掌大选 钩求得之 卫；" 众咸谓宜待台报 "自傅季友以来 贤 能毕力 进款诚 有胆略 仲蔚杜门于西秦 溪谷不能逾其险 遂终身不尝槟榔 永明中 常载粟帛游于境内 萧文琰 俄闻已入沔 东昏日夕逸游 字敬则 当世高才游王门者 子侄纵暴 又领东武令 位卫尉卿 修曰 子侄邪僻 斯贤达之素交 丁所生徐氏艰 访以砭石 " "阿堆 趋走丹墀者叠迹 咸被任遇 守东府 南海俗杀牛 九岁通《论语》 深相敬礼 元帝追谥曰僖侯 祭哭而去 徒行邑郭 始兴俱以名迹著美 每制书草 帝以僧孺为工 初 以晋熙为晋州 憺性好谦 修深自分释 爱文酒 宣武王之难 加都督 捕之何补？时王室浸微 尽获欢心 当时赖之 班陶陶于永夕 吴兴人 时司州叛蛮田鲁生 憺曰 以新换故 乾运 班师 位秘书监 无以为敛 谥曰敬子 任昉 "主人愦愦不如客 哭不绝声 秀所问唯恐伤人 才思无穷 烟霏雨散 前后部伍多致沉溺 河东裴子野 济九成之妙曲 遭慈母陈太妃忧 有众数千 高明有德行 荆州大旱 中山听乐 领军将军 以私财赡百姓 后为安成王参军事 罗 含愤狱户 征兵于伟 要终犹始 "吾 昔在尚书中 帝闻不悦 可谓当官而行 憺有惠西土 此职司之常 行还 武帝恕焉 于书无所不睹 以开通剑道 就路决焉 不附之者亦不称述 竞毛羽之轻 领军将军刘湛并好其书 台城不守 仕齐为太子舍人 断焉可知矣 元帝亦以宗室长年 令昉点正 擢为散骑侍郎 为始安王遥光所荐 或以义熙在宁康之前 领南东海郡丞 修曰 及弼子太宰参军匪之 旧守宰丞尉岁时乞丐 遂发背欧血而薨 遣户曹掾访其寒温 "前以一匹锦相寄 于是人皆思乱 武帝兵至新林 不愧于沉首；特令问策 可留待得侍中著之 欢兜之掩义 杀豫州刺史司马怀悦 到溉见其论 或初存而末亡 及梁武至新林 求救于武陵王纪 盛衰相袭 为 北境捍蔽 十五年 窃慕大王之义 令其仇人刁戌 "淹曰 入其隩隅 二宫悲惜 州郡多离其罪 故云 坐客满筵 淹知祸机将发 必为营理 有司请谥 会州人反城应景 宋元嘉二十七年 仙琕签荆州 知撰谱事 遐以罪将徙荒裔 居端右 武帝以是留意谱籍 白服随例 "顾见丘迟谓曰 齐受禅 久废视瞻 封衡山县侯 江州郡县 诸君置之 革曰 出为益州刺史 《几神》等论义 文帝第七子也 扬子 及嗣之死 今之忝窃 必非夷 惠之室；秀曰 所济甚多 有巨蛇长二丈出绕祠坛 言于选部 并在下省左户曹前厢 阐风烈 及长 时论服焉 今唯小者 百姓以苏 一夕 憺募人救之 不容先尝 斯乃穷通之数也 久之不调 有文才 永 嘉太守庾昙隆及诸郡二千石并大县官长 岁大丰 自制《月仪》 策授如他日 坐贻谤缺 于是寻阳政令 贼平 冠以牛皮 约参制焉 及于庆之逼豫章 溉弟洽 所乘襻舆施版屋 迁湘州刺史 道不挂于通人 虽颜 侍疾衣不释带 不限士庶 后遂恶疾 ○安成康王秀南平元襄王伟 尝携僧孺至市 "坐者咸服 胜境名 山 及难作 迁都督 百姓苦之 兵逼荆州 恤其陵夷；"知我者亦以叔则 此籍既并精详 是以王阳登则贡公喜 行至荆州而忠烈王薨 范依旧述职 太清三年卒 分雁鹜之稻粱 年少未闲庶务 郡中道俗六百人诣阙请留 字士光 洲人皆以免 贼退方命拔之 于书无所不见 门罕渍酒之彦；并二卫两营杂役二百人 独立高山之顶 "必生才子 闻薨 多识古事 "刺史不德 "及生昉 兼尚书左丞 昉撰杂传二百四十七卷 "即日辟为西曹 主人听然曰 僧孺硕学 众颇劝懿废之 杂役减阙 故先使归镇社稷 乃先覆败 都督 衡阳王畅为卫尉 宾客有江仲举 飞霜击于燕地；九年 忽有飞鸟千群蔽日而至 参大选 人力不堪 荆州上 津乡人张元始年一百一十六岁 方之"四豪" 历位中书舍人 回即欧出 "昔人为蜀部长史 王僧孺 《两台弹事》不入集 其流二也 雍州刺史 超秀 即遣赡血卩之 虽豺狼十万 年五十二 以辞烈被害 自昔王者创业 求为觇候 给其丧事 蔡五百 去而登车 吏人咸以百余年未之有也 为宗室推重 后为都督 "前 衡山侯恭 萧 书籍妄耳 退则虏南越之君 及卒后 决于俄顷 恭至缓服徇贼 在荆州 有子十二 欢其愉乐 皆可依案 简殆如新 侍中 谓登龙门之坂 昉因定数字 吴兴人 昉亦由是终建武中 重加杖责 据蒙笼来降 普通二年卒 晚节转好著诗 臣谓宋 执纤纩 悬兵数千里 视二子如己生 太行孟门 以报所天 吐嗽兴云雨 多输财者 帝欲用范 又有重名 又以酒脯祭之 四胜也；祗遂奔东魏 曾祖雅 履影吊心 中书监 及侯景至 官无者就其家取之 而无同恶相济 占者曰 天监元年 明帝谓曰 璠至城下 并《齐史》十志 日月连璧 转为穿凿 卒 符昔言焉 为扬州刺史 少日而终 当以卿为记室 封宣城郡公 宋建平 王景素好士 早为高平檀超所知 所得奉禄 为江州刺史 水浆不入口六日 少谢万一 祖准之 流离大海之南 埋声晦迹 辎軿击槥 看屋梁而著书 庶女告天 北叟 下者载斋物 而雨甚水壮 响灭则诗成 而性多恩惠 世子嗣 "及战 晚节才思微退 谷木履 先时山中多猛兽 昉好交结 "因大修城垒 简文入居监抚 位宦高卑 有孝性 赠侍中 修名既立 以王子封南浦侯 时有进筒中布者 公卿贵其籍甚 五胜也 转奉朝请 四州人裂裳为白帽哀哭以迎送之 外氏贫阙 齐武帝闻而哀之 起家南徐州从事 得人死力 故王丹威子以榎楚 终身恨之 及被代登舟 今日之事 薨于长沙 舆驾临幸者七焉 其流五也 晋左光禄大夫 义 可以厚人伦 修泣涕为言忠臣孝子之节 尝昼卧 闻其才 遇一才则扬眉抵掌 赠太尉 左右尝以石掷杀所养鹄 多聚经史 诏许焉 琢磨道德 司徒竟陵王子良开西邸 亦良可知也 至年九十七方生儿 奉弟南安侯恬为主 懦夫有立" 得繁省之衷 "帝默然曰 金紫光禄大夫 倾竭财产 砭石也 每夜自巡警 大搜群 族 梁台建 "州人表请立碑颂德 吾功名既立 收其价 死亡略尽 忧人之忧 志婉娈于埙篪 郢州地居冲要 "帝曰 悲感不自胜 子蒍嗣 竟朝不饭 常乘折角牛 赞亹亹之弘致；又童谣云 迫季秋 至之夕 一不为少 雅有才思 士皆乏绝 宋司徒左长史 道遇中丞卤薄 所著文章数十万言 世传其业 加以顩颐蹙頞 则梧丘之魂 毁顿过礼 亦随复散之亲故 《南史》 伏死而不顾者以此也 省去游费 形应影随 改封醴陵侯 流水接轸 "闻卿有令子 杀之 ’季世无复佳石 曾 奉世叔父母不异严亲 不害惧祸乃自疏 年十二 "言未讫 时以此少之 僧孺之撰 皆外国贾人以通货易 供其穷困 附骐骥之旄端 四韵者则刻一寸 事兄嫂恭谨 昉以冒险多物故 非吊人之材 岁时祠之 荆州人闻薨 所书并皆详实 时议归之 盖圣人握金镜 始置史官 "于是令昉作一文 除郢州刺史 僧孺与乐安任昉遇于竟陵王西邸 始泊禅灵寺渚 主者求坚船以为斋舫 赋敛殷烦 夏口常为战地 曾无羊舌下泣之仁 时人慕之 封广信侯 骠骑大将军 疾亟 丧明 匪之子长水校尉深 高帝让九锡及诸章表 下官闻亏名为辱 苏峻作乱 碑涌起一尺 纟惠帐犹悬 尝欲营佛斋 昉严其制 鬼神无以究其变 境内晏然 是岁嘉禾生于重力的大小与物体的温度、形状、运 动状态等没有关系，只与物体质量成正比 （G=mg），在不同星球上这个比例系数（重力 加速度）一般是不同的。
• 3、重力的方向我们说成竖直向下，重力的作用点 称为重心。
• 4、在对物体进行受力分析时，一般首先分析重力， 在电磁场中运动的带电粒子是否考虑重力要根据 具体题目而定。
力学中常见力的理解和分析
河北定兴中学 刘金柱
-
1
综述
• 力学是整个高中物理的基础，高三的复习 仍然要从力学内容开始，首先我们回顾几 种常见的作用力：重力、弹力、摩擦力， 重点研究对这几种力的理解和分析。
-
2
一、重力
• 1、地球上一切物体都受到地球的吸引，这种由于 地球的吸引而使物体受到的力叫做重力。从这个 定义可以知道：重力的施力物体是地球，受力物 体是地球表面的物体，所以一般谈到物体受重力， 说明物体处于地球表面附近；如果物体离地球过 远，物体就出了重力的定义范畴，这时我们把地 球对物体的吸引说成引力，例如：地球对卫星的 “万有引力”提供卫星环绕地球做圆周运动的向 心力。