指导书第六章角度调制系统习题详解
- 格式:doc
- 大小:1.65 MB
- 文档页数:31

第5章 角度调制与解调思 考 题8.1 已知载波f c =100MH Z ,载波电压振幅U cm =5V ,调制信号u Ω(t )= ( cos2π×103t +2cos2π×500t )V 。
试写出下述条件调频波的数学表达式:(1) 频灵敏度K f =1kH Z /V 。
(2)频偏△f m =20kH Z 。
解:(1)⎥⎦⎤⎢⎣⎡+=⎰Ωtt fc cm t FM dt u k t U u 0)()(cos ω⎥⎦⎤⎢⎣⎡⨯⋅⨯+⨯⋅⨯+⨯⨯⨯=⎥⎦⎤⎢⎣⎡⨯+⨯+=⎰⎰t t t tdt ktdt kt f t t ffc 5002sin 50022000102sin 10210001010014.32cos 55002cos 2102cos 2cos 53363πππππππ()t t t 5002sin 64.0102sin 16.01028.6cos 538⨯+⨯+⨯=ππ(2)因为max )(2t u k f f m m Ω=∆=∆πω 所以V KHz t u f k m f /8.622102014.32)(23max=⨯⨯⨯=∆=Ωπ所以()tt t dt t u k t U t u tfc cm FM 5002sin 40102sin 101028.6cos 5)(cos )(380⨯+⨯+⨯=⎥⎦⎤⎢⎣⎡+=⎰Ωππω8.2 载波振荡频率f c =25MH Z ,振幅U cm =4V ;调制信号为单频余弦波,频率为F =400H Z ;最大频偏△f m =10kH Z 。
(1) 分别写出调频波和调相波的数学表达式。
(2) 若调制频率变为2 kH Z ,其他参数均不变,再分别写出调频波和调相波的数学表达式。
解:(1)因为F m f f m ⋅=∆,所以rad KHzKHzFfm mf 254.010==∆=所以:()()()tt Ft t f t m t U t u c f c cm FM 38105.2sin 251057.1cos 42sin 252cos 4sin cos )(⨯+⨯=+=Ω+=ππω()()tt t m t U t u P c cm PM 38105.2sin 251057.1cos 4cos cos )(⨯+⨯=Ω+=ω(2)如果F=2KHz ,则radKHzKHz m m P f 5210===近而可写出调频波和调相波的数学表达式:()()()tt Ft t f t m t U t u c f c cm FM 38105.2sin 51057.1cos 42sin 52cos 4sin cos )(⨯+⨯=+=Ω+=ππω()()tt t m t U t u P c cm PM 38105.2sin 51057.1cos 4cos cos )(⨯+⨯=Ω+=ω8.3若调频波的中心频率f c =100MH Z ,最大频偏△f m =75kH Z ,求最高调制频率F max 为下列数值时的m f 和带宽:(1) F max =400 H Z ;(2) F max =3kH Z ;(3) F max =15kH Z 。

第5章 角度调制与解调思 考 题8.1 已知载波f c =100MH Z ,载波电压振幅U cm =5V ,调制信号u Ω(t )= ( cos2π×103t +2cos2π×500t )V 。
试写出下述条件调频波的数学表达式:(1) 频灵敏度K f =1kH Z /V 。
(2)频偏△f m =20kH Z 。
解:(1)⎥⎦⎤⎢⎣⎡+=⎰Ωt t f c cm t FM dt u k t U u 0)()(cos ω (2)因为max )(2t u k f f m m Ω=∆=∆πω 所以V KHz t u f k m f /8.622102014.32)(23max =⨯⨯⨯=∆=Ωπ 所以()t t t dt t u k t U t u t f c cm FM 5002sin 40102sin 101028.6cos 5)(cos )(380⨯+⨯+⨯=⎥⎦⎤⎢⎣⎡+=⎰Ωππω8.2 载波振荡频率f c =25MH Z ,振幅U cm =4V ;调制信号为单频余弦波,频率为F =400H Z ;最大频偏△f m =10kH Z 。
(1) 分别写出调频波和调相波的数学表达式。
(2) 若调制频率变为2 kH Z ,其他参数均不变,再分别写出调频波和调相波的数学表达式。
解:(1)因为F m f f m ⋅=∆,所以rad KHz KHz F f m m f 254.010==∆=所以:()()()t t Ft t f t m t U t u c f c cm FM 38105.2sin 251057.1cos 42sin 252cos 4sin cos )(⨯+⨯=+=Ω+=ππω(2)如果F=2KHz ,则rad KHzKHz m m P f 5210=== 近而可写出调频波和调相波的数学表达式:8.3若调频波的中心频率f c =100MH Z ,最大频偏△f m =75kH Z ,求最高调制频率F max 为下列数值时的m f 和带宽:(1) F max =400 H Z ;(2) F max =3kH Z ;(3) F max =15kH Z 。


第六章思考题与习题解答6-1 要满足下列要求,应引入何种反馈?(1)稳定静态工作点;(2)稳定输出电压;(3)稳定输出电流;(4)提高输入电阻;(5)降低输入电阻;(6)降低输出电阻、减小放大电路对信号源的影响;(7)提高输出电阻、提高输入电阻。
目的复习引入反馈的原则。
解(1)欲稳定静态工作点应引入直流负反馈,因为静态工作点是个直流问题。
(2)稳定输出电压应引入电压负反馈。
输出电压是交流参量,电压负反馈属于交流反馈组态。
在四种交流负反馈组态中,电压串联负反馈和电压并联负反馈均能达到稳定输出电压的目的。
(3)稳定输出电流应引入电流负反馈。
输出电流也是交流参量,在四种组态中,引电流串联负反馈或电流并联负反馈均可。
(4)提高输入电阻应引入串联负反馈,如电压串联负反馈或者电流串联负反馈。
(5)降低输入电阻应引入并联负反馈,如电压并联负反馈或者电流并联负反馈。
(6)降低输出电阻、减小放大电路对信号源的影响是一个减小输出电阻并提高输入电阻的问题,应引入电压串联负反馈。
(7)输入、输出电阻均提高应引入电流串联负反馈。
6-2 负反馈放大电路为什么会产生自激振荡?产生自激振荡的条件是什么?解在负反馈放大电路中,如果把负反馈引的过深会将负反馈变成正反馈,于是自激振荡就产生了。
产生自激振荡的条件是AF=-1幅度条件AF=1相位条件arg AF=±(2n+1)π,n为整数∆=±180°或者附加相移φ6-3 判断下列说法是否正确,用√或×号表示在括号内。
(1)一个放大电路只要接成负反馈,就一定能改善性能。
( )(2)接入反馈后与未接反馈时相比,净输入量减小的为负反馈。
( )(3)直流负反馈是指只在放大直流信号时才有的反馈;( )交流负反馈是指交流通路中存在的负反馈。
( )。
(4)既然深度负反馈能稳定放大倍数,那么电路所用各个元件都不必选用性能稳定的。
( )(5)反馈量越大,则表示反馈越强。



第6章 角度调制与解调电路6.1填空题(1) 用低频调制信号去改变载波信号的频率和相位,分别称为 调频 和 调相 ,它们都是频谱的 非线性 变换。
(2) 单频调制时,调频信号的调频指数m f 与调制信号的 振幅 成正比,与调制信 号的 频率 成反比;最大频偏Δf m 与调制信号的 振幅 成正比,与 频率 无关。
(3) 取差值的混频器输入信号为u s (t)=0.3cos[(2π×107t )+7sin(2π×103t)]V ,本振信号u L (t)=cos(2π×1.2×107t)V ,则混频器输出信号的载频为 0.2×107 Hz ,调频指数m f 为 7 ,最大频偏Δf m 为 7 ×103 Hz ,频带宽度为 16 ×103 Hz 。
(4) 3倍频器输入调频信号u s (t)=U sm cos[(2π×105t)+2sin(2π×102t)]V ,则3倍频器输出信号的载频为 3×105 Hz ,最大频偏为 3× 2 ×102 Hz ,频带宽度为 14×102 Hz 。
(5) 斜率鉴频是先将调频信号变换成 调频调幅 信号,然后用 包络检波器 进行解调得到原调制信号。
(6) 乘积型相位鉴频器由 频相变换网络 、 相乘器 和 低通滤波器 等组成。
6.2 已知调制信号3()8cos(2π10)V u t t Ω=⨯,载波电压6()5cos(2π10)V c u t t =⨯,3f 2π10rad/s V k =⨯,试求调频信号的调频指数f m 、最大频偏m f ∆和有效频谱带宽BW ,写出调频信号表示式。
[解] 3m 3m 2π108810Hz 2π2πf k U f Ω⨯⨯∆===⨯3m 33632π1088rad 2π102(1)2(81)1018kHz ()5cos(2π108sin 2π10)(V)f f FM k U m BW m F u t t t Ω⨯⨯===Ω⨯=+=+⨯==⨯+⨯6.3 已知调频信号72()3cos[2π105sin(2π10)]V o u t t t =⨯+⨯,3f 10πrad/s V k =,试:(1) 求该调频信号的最大相位偏移f m 、最大频偏m f ∆和有效频谱带宽BW ;(2) 写出调制信号和载波电压表示式。



第一章绪论1、填空题(1)一个完整的通信系统应包括(2)在接受设备中,检波器的作用是(3)调制时用音频信号控制载波的(4)无线电波传播速度固定不变,频率越高,波长?,频率?,波长越长。
(5)短波的波长较短,地面绕射能力?,且地面吸收损耗?,不宜?传播,短波能被电离层反射到远处,主要以?方式传播。
(6)波长比短波更短的无线电波称为?,不能以?和?方式传播,只能以?方式传播。
2.判断题(1)低频信号可直接从天线有效地辐射。
(2)高频电子技术所研究的高频工作频率范围是300KHz~3000MHz.(3)为了有效地发射电磁波,天线尺寸必须与辐射信号的波长相比拟。
(4)电视、调频广播和移动通信均属于短波通信。
第二章小信号调谐放大器1、填空题(1)衡量谐振电路选频性能的指标有???。
(2)实际谐振曲线偏离理想谐振曲线的程度,用?指标来衡量。
(3)谐振回路的品质因数Q 愈大,通频带愈?,选择性愈?。
(4)已知LC并联谐振回路的电感L在f=30MHz时测得L=1Uh,Q0=100。
求谐振频率f0=30MHz 时的电容C=?和并联谐振电阻R0=?。
(5)小信号谐振放大器的集电极负载为?。
( 6)小信号谐振放大器多级级联后,增益? ,计算式为? ;级联后通频带? ,若各级带宽相同,则计算式为?。
(7)小信号谐振放大器双调谐回路的带宽为单调谐回路带宽的?倍。
( 8)调谐放大器主要由?和? 组成,其衡量指标为?和?。
( 9)晶体管在高频工作时,放大能力?。
晶体管频率参数包括?、?、?、?。
(10)所谓双参差调谐,是将两级单调谐回路放大器的谐振频率,分别调整到?和?信号的中心频率。
2、选择、判断题(1)对于小信号谐振放大器,当LC谐振回路的电容增大时,谐振频率的回路品质因数都增加。
为什么?⑵题(1)中,当LC谐振回路的电感增大时,谐振频率和回路的品质因数都减小。
为什么?(3)在相同条件下,双调谐回路放大器和单调谐回路放大器相比,下列表达正确的是() 双调谐回路放大器的选择性比单调谐回路放大器好,通频带也较窄。
兰州交通大学《通信原理》精品课程/txyl09/index.htm第一章绪论本章主要内容:(1)通信系统的模型与基本概念(2)通信技术的现状与发展(3)信息的度量(4)通信系统的主要性能指标本章重点:1.通信系统的一般模型与数字通信系统模型2.离散信源的信息量、熵的计算3.数字通信系统的主要性能指标:码元传输速率与信息传输速率以及它们的关系、误码率与误信率本章练习题:1-1.已知英文字母e出现的概率为0.105,x出现的概念为0.002,试求e和x的信息量。
•查看参考答案o1-2.某信源符号集由A,B,C,D和E组成,设每一符号独立出现,其出现概率分别为14,18,1 8,316和516。
试求该信息源符号的平均信息量。
•查看参考答案o1-3.设有4个符号,其中前3个符号的出现概率分别为14,18,18,且各符号的出现是相对独立的。
试计算该符号集的平均信息量。
•查看参考答案o1-4.一个由字母A 、B 、C 、D 组成的字,对于传输的每一个字母用二进制脉冲编码,00代替A ,01代替B ,10代替C ,11代替D ,每个脉冲宽度为5ms .(1)不同的字母是等可能出现时,试计算传输的平均信息速率;(2)若每个字母出现的可能性分别为 103,41,41,51====D C B A P P P P试计算传输的平均信息速率。
• 查看参考答案o1-5.国际摩尔斯电码用“点”和“划”的序列发送英文字母,“划”用持续3单位的电流脉冲表示,“点”用持续1个单位的电流脉冲表示;且“划”出现的概率是“点”出现概率的13。
(1)计算“点”和“划”的信息量;(2)计算“点”和“划”的平均信息量。
• 查看参考答案o1-6.设一信息源的输出由128个不同的符号组成,其中16个出现的概率为132,其余112个出现概率为1224。
信息源每秒发出1000个符号,且每个符号彼此独立。
试计算该信息源的平均信息速率。
• 查看参考答案o1-7.设一数字传输系统传送二进制码元的速率为2400B ,试求该系统的信息速率;若该系统改为传送16进制信号码元,码元速率不变,则这时的系统信息速率为多少(设各码元独立等概率出现)?• 查看参考答案o1-8.若题1―2中信息源以1000B 速率传送信息。
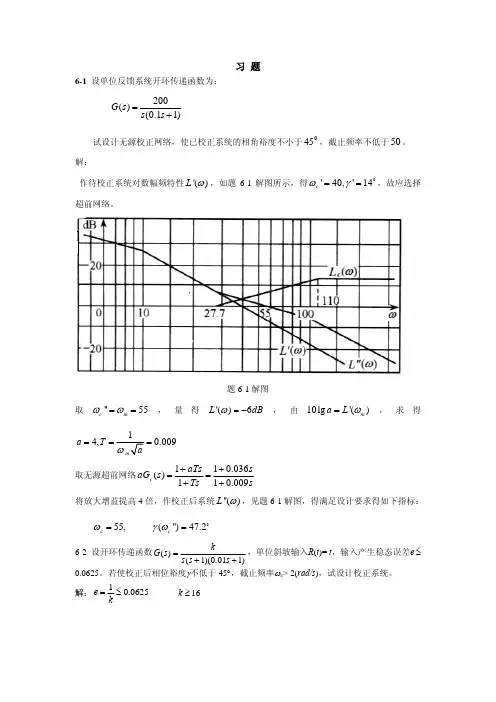
第六章 线性系统的校订习题与解答6-1 设有单位反应的火炮指挥仪伺服系统,其开环传达函数为G(s)Ks( 0. 2s 1)(0.5s 1)若要求系统最大输出速度为2(r / min),输出地点的允许偏差小于 2o,试求: ( 1)确立知足上述指标的最小K值,计算该K值下系统的相角裕度和幅值裕度;( 2)在前向通路中串接超前校订网络 G c ( s)0.4 s 10.08s 1计算校订后系统的相角裕度和幅值裕度,说明超前校订对系统动向性能的影响。
解 (1) 确立知足 C Max2(转 / 分) =120 / 秒和 e ss 20 的 K , , h :CMax6( 1/ 秒)K K VessG (s)61)(0.5s 1)s( 0.2s作系统对数幅频特征曲线如图解 5-32(a) 所示:由图可知c2 6 3.46' 90o arctg 0.2 c ' arctg0.5 c ' 3.8o算出相角交界频次g'3.220 lg h' 1( dB)图 6-1a图 6-1b(2) 超前校订后系统开环传达函数为6(0. 4s1)G c (s)G ( s)1)( 0.5s 1)s(0.08 s 1)( 0.2s作校订后系统对数幅频特征曲线如图解图6-1b 所示,由图得:62.5 ,c26 24.8c2.5" 90oarctg 0.4c"arctg 0.2 c " arctg 0. 08 c " arctg0.5 c " 22.5o算出g " 7.3 ,h 2.371 , 20lg h" 7.5dB 。
说明超前校订能够增添相角裕度, 从而减小超调量, 提升系统稳固性; 同时增大了截止频次,缩短调理时间,提升了系统的迅速性。
6-2设单位反应系统的开环传达函数为G(s)K s(s1)试设计一串连超前校订装置,使系统知足以下指标:( 1)在单位斜坡输入下的稳态偏差 ess115;( 2)截止频次 ω c ≥ 7.5(rad/s) ; ( 3)相角裕度 γ ≥ 45°。
第6章 角度调制与解调电路6.1 已知调制信号38cos(2π10)V u t Ω=⨯,载波输出电压6o ()5cos(2π10)V u t t =⨯,3f 2π10rad/s V k =⨯g ,试求调频信号的调频指数f m 、最大频偏m f ∆和有效频谱带宽BW ,写出调频信号表示式[解] 3m 3m 2π108810Hz 2π2πf k U f Ω⨯⨯∆===⨯3m 33632π1088rad2π102(1)2(81)1018kHz ()5cos(2π108sin 2π10)(V)f f o k U m BW m F u t t t Ω⨯⨯===Ω⨯=+=+⨯==⨯+⨯6.2 已知调频信号72()3cos[2π105sin(2π10)]V o u t t t =⨯+⨯,3f 10πrad/s V k =g ,试:(1) 求该调频信号的最大相位偏移f m 、最大频偏m f ∆和有效频谱带宽BW ;(2) 写出调制信号和载波输出电压表示式。
[解] (1) 5f m =5100500Hz=2(+1)2(51)1001200Hzm f f m F BW m F ∆==⨯==+⨯=(2) 因为mf f k U m Ω=Ω,所以352π1001V π10f m fm U k ΩΩ⨯⨯===⨯,故27()cos 2π10(V)()3cos 2π10(V)O u t t u t t Ω=⨯=⨯6.3 已知载波信号m c ()cos()o u t U t ω=,调制信号()u t Ω为周期性方波,如图P6.3所示,试画出调频信号、瞬时角频率偏移()t ω∆和瞬时相位偏移()t ϕ∆的波形。
[解] FM ()u t 、()t ω∆和()t ϕ∆波形如图P6.3(s)所示。
6.4 调频信号的最大频偏为75 kHz ,当调制信号频率分别为100 Hz 和15 kHz 时,求调频信号的f m 和BW 。
[解] 当100Hz F =时,37510750100m f f m F ∆⨯===2(1)2(7501)100Hz 150kHz f BW m F =+=+⨯= 当15kHz F =时,33751051510m f f m F ∆⨯===⨯32(51)1510Hz 180kHz BW =+⨯⨯=6.5 已知调制信号3()6cos(4π10)V u t t Ω=⨯、载波输出电压8()2cos(2π10)V o u t t =⨯,p 2rad /V k =。
第六章 角度调制系统6-1设角度调制信号()()0cos 200cos m S t A t t ωω=+ ①若()S t 为FM 波,且4F K =,试求调制信号()f t ; ②若()S t 为PM 波,且4P K =,试求调制信号()f t ; ③ 试求最大频偏max |FM ω∆及最大相位移max ()|PM t ϕ。
解:①FM 已调信号瞬时相位为0()200cos m t t t θωω=+,对其取导数得到瞬时角频率为00()()(200)sin ()m m F d t t t K f t dtθωωωωω==+-=+ 因此调制信号为()50sin m m f t t ωω=-② PM 已调信号瞬时相位为00()200cos ()m P t t t t K f t θωωω=+=+因此调制信号为()50cos m f t t ω=③ 由FM 信号瞬时频率0()(200)sin m m t t ωωωω=+-,可得最大频偏为m FM ωω200|max =∆由PM 信号瞬时相位t t m ωϕcos 200)(=,可得最大相偏为200|)(max =PM t ϕ6-2用频率为10kHz ,振幅为1V 的正弦基带信号,对频率为100MHz 的载波进行频率调制,若已调信号的最大频偏为1MHz ,试确定此调频信号的近似带宽。
如果基带信号的振幅加倍,此时调频信号的带宽为多少?若基带信号的频率加倍,调频信号的带宽又为多少? 解:①由题目可知6110f Hz ∆=⨯ ,4110m f Hz =⨯ 。
根据卡森带宽公式可以得到调频信号的带宽近似为Hz f f B m FM 61002.2)(2⨯=+∆≈② 以单音调制为例:m F A K =∆ω。
当A m 加倍时,ω∆加倍,故此时调频信号最大频偏为Hz f 6102'⨯=∆其带宽近似为Hz f f B m FM 61002.4)'(2⨯=+∆≈③m f 加倍,Hz f f m m 310202'⨯==,则调频信号带宽近似为Hz f f B m FM 61004.2)'(2⨯=+∆≈6-3将正弦信号m(t)=cos2πf m t 进行角度调制,若载频f c =100 Hz ,f m =f c /4。
①调相灵敏度K P =π rad/s ,画出m(t)和对应PM 信号; ②调频灵敏度K F =π rad/s ·V ,画出m(t)和对应FM 信号。
解:① m(t)=cos2πf m t ,对应PM 信号为0()cos(cos2t)PM m S t A t f ωππ=+其瞬时角频率为2()(cos2)'2sin(2)m m m t f t f f t ωππππ∆==-,作图如下:② m(t)=cos2πf m t ,对应FM 信号为01()cos(sin 2t)2FM m mS t A t f f ωπ=+其瞬时角频率为()()cos2m t m t f t ωπππ∆==,作图如下:6-4已知某FM 调制器的频移常数V Hz K F /10=,载波幅度为1V ,载波频率为1000Hz ,调制信号)2cos()(t f A t f m m π=。
试画出以下几种情况下已调信号的幅度谱。
①Hz f V A m m 200,2==; ②Hz f V A m m 20,2==; ③Hz f V A m m 4,2==; ④Hz f V A m m 20,10==。
解:①由于Hz f V A m m 200,2==,因此调频指数为1020.1200F m FM m K A f β⨯=== 已调信号频谱为00()J ()[()()]J(0.1)[(210002200)(210002200)]FM n FM m m n nn S A n n n n ωπβδωωωδωωωπδωππδωππ+∞=-∞+∞=-∞=--+++ =-⨯-⨯⨯++⨯+⨯⨯∑∑ 作图如下:②Hz f V A m m 20,2==,因此调频指数为102120F m FM m K A f β⨯=== 已调信号频谱为00()J ()[()()]J(1)[(21000220)(21000220)]FM n FM m m n nn S A n n n n ωπβδωωωδωωωπδωππδωππ+∞=-∞+∞=-∞=--+++ =-⨯-⨯⨯++⨯+⨯⨯∑∑作图如下:③Hz f V A m m 4,2==,因此调频指数为10254F m FM m K A f β⨯=== 已调信号频谱为00()J ()[()()]J(5)[(2100024)(2100024)]FM n FM m m n nn S A n n n n ωπβδωωωδωωωπδωππδωππ+∞=-∞+∞=-∞=--+++ =-⨯-⨯⨯++⨯+⨯⨯∑∑作图如下:④Hz f V A m m 20,10==,因此调频指数为1010520F m FM m K A f β⨯=== 已调信号频谱为00()J ()[()()]J(5)[(21000220)(21000220)]FM n FM m m n nn S A n n n n ωπβδωωωδωωωπδωππδωππ+∞=-∞+∞=-∞=--+++ =-⨯-⨯⨯++⨯+⨯⨯∑∑作图如下:6-5若某角度调制信号由下式描述:38210()10cos[10cos(210)]t s t t ππ⨯⨯=+⨯ 确定以下各值:①已调信号的功率; ②最大相位偏移; ③最大频率偏移。
解:①已调信号的功率为2210()502P s t W =≈=②瞬时相位偏移为310cos(210)t π⨯最大相位偏移为max ()|10t rad ϕ=③瞬时频率偏移为33()10210sin(210)t t ωππ∆=-⨯⨯⨯最大频率偏移4max ()|210/t rad s ωπ ∆=⨯6-6设某角度调制信号为()()510cos 21010cos 2000S t t t ππ=⨯+,试确定:① 已调信号的平均功率;② 最大频率偏移; ③ 最大相位偏移;④ 已调信号的近似带宽;⑤ 判断该已调信号是FM 波还是PM 波。
解:①已调信号的平均功率为2210()502S S t W =≈=②信号瞬时频率为5()210102000sin 2000t t ωπππ=⨯-⨯因此信号最大频偏为4max 210/rad s ωπ∆=⨯③瞬时相位偏移为10cos 2000t π因此信号最大相位偏移为max ()|10t rad ϕ=④根据卡森带宽,43max 2()2(2102000)22210/22FM m FM W rad s B kHzωωπππ=∆+=⨯⨯+=⨯⨯=⑤ 根据已调信号表达式判断是FM 波还是PM 波,主要依据是瞬时相偏与调制信号成正比还是瞬时频偏与调制信号成正比。
根据题目所给,在未知调制信号是正弦波还是余弦波的情况下,该已调信号既可能是正弦波作FM 调制,也可能是余弦波作PM 调制。
因此,不能判断是FM 波还是PM 波。
6-7在50Ω的负载上有一个角度调制信号,其时间函数为)]102sin(310cos[10)(38t t t s ⨯+=ππ V 求信号的总平均功率、最大频率偏移和最大相位偏移。
解:信号的总平均功率为2210()502P s t W =≈=信号瞬时频偏为33()3210cos(210)t t ωππ∆=⨯⨯⨯因此最大频率偏移为3max ()|32106000/t rad s ωππ∆=⨯⨯=信号瞬时相位偏移为3()3sin(210)t t ϕπ∆=⨯因此最大相位偏移为3 rad 。
6-8 用频率为1kHz 的正弦信号对频率为200kHz 的载波进行调频,设峰值频偏为150Hz ,试求:① 调频信号的带宽;② 上述调频信号经16倍频后的带宽;③ 在经过16倍频后,调频信号中的有效边频数目。
解:①已知Hz f Hz f Hz f m 150,10200,100030=∆⨯==,由卡森带宽公式得到调频信号带宽为kHz f f B m FM 3.2)(2=∆+=②倍频后,载频0f 和峰值频偏f ∆均为原来的16倍,因此这时调频信号带宽为kHz f f B m FM 8.6)16(2=∆+=③倍频后,调频指数16'mf f β∆=增为原来的16倍,而倍频前的调频指数15.0=∆=m f fβ,所以倍频后有效边频数'116 3.4n β>+=。
取为4。
6-9将幅度为4V 、频率为1kHz 的正弦调制波形输入调频灵敏度为50 Hz/V 的FM 调制器中,试问:①峰值频率偏移是多少? ②调制指数是多少?解:①正弦调制波形可表示为()4cos(21000)m t t π=⨯已知50/100/()F K Hz V rad s V π= = ⋅。
因此,瞬时频率偏移为()()400cos(21000)F t K m t t ωππ∆==⨯峰值频率偏移(即最大频率偏移)为max ()|400/t rad s ωπ∆=②调制指数为10040.221000F mFM mK A πβωπ⨯===⨯。
6-10已知调频信号()()6310cos 108cos10FM S t t t ππ=+,调制器的频率偏移常数2FM K =,试求:① 载波频率0f ;② 调频指数;③ 最大频率偏移; ④调制信号()f t 。
解:①由)(t S FM 的表达式知:载频60100.52f MHz ππ== ②瞬时相位偏移t t πϕ310cos 8)(=,故8|)(max ==t FM ϕβ ③瞬时频率偏移)10sin(108)()(33t dtt d t ππϕω⨯-==∆, 故最大频偏33max max 810/,410rad s f Hz ωπ∆=⨯ ∆=⨯ 。
④瞬时频率为6330()()10810sin(10)()F d t t t K f t dtθωπππω==-⨯=+ 已知2FM K =,因此调制信号为33()410sin(10)f t t ππ=-⨯6-11用幅度为1V 、频率为500Hz 的正弦信号,对幅度为3V 、频率为1MHz 的载波信号进行调频时,最大频偏为1kHz 。
若调制信号的幅度增加为5V ,且频率增至2kHz ,试写出此时调频信号的表达式。
解:调制信号可表示为()cos(2500)f t t π=⨯,载波信号可表示为6()3cos(210)c t t π=⨯。
要求最大频偏为1kHz ,因此频移常数为3max 210002101FM m K A ωππ∆⨯===⨯ 当调制信号的幅度增加为5 V ,且频率增至2 kHz 时,可表示为)20002cos(5)(t t f ⨯=π这时调频信号表达式为0366'()3cos(sin ')'21053cos[210sin(22000)]220003cos[210 2.5sin(22000)]F m FM m m K A S t t t t t t t ωωωππππππ=+⨯⨯ =⨯+⨯⨯ =⨯+⨯6-12已知调频信号为为01122()cos[2sin(2)sin(2)]FM S t A f t f t f t πβπβπ=++,其中088f MHz =,15f kHz =,23f kHz =,122ββ==,试:①画出调频波的频谱结构图(考虑大于未调载波幅度1%的边频分量); ②计算各频谱分量的总功率,并与调频波总功率相比。