2012 大学生数学竞赛试题

2012年天津市大学数学竞赛试题（经管类）一、填空题（共15分，每空3分）1．设1e 12sin )(1)(3--+=x x x f x f ，则极限=→)(lim 0x f n ． （ 6 ）2．设函数)(x f 连续切不等于0，又⎰+=C x x x xf arcsin d )(，则=⎰)(d x f x． （ C x +--232)1(31 ）3．半径为R 的无盖半球形容器中装满了水，然后慢慢地使其倾斜3π，则流出的水量=V ． （3833R π ） 4．设函数)(x f 可微，且1)0(0)0(='=f f ，，又设平面区域222t y x D ≤+：，则=+⎰⎰+→σd )(1lim 223Dt y x f t ． （32π ） 5．设函数)(x f 在点0=x 处二阶可导，且2cos 1)(lim0=-→xx f x ，则='')0(f ．（ 2 ） 二、单项选择题（共15分，每空3分）1．设函数)(x f 有连续导数，3)0(1)0(='=f f ，，则极限=→xx x f 21)]([lim （ ）．(D)（A ）1 （B ）e （C ）3/2e（D ）2/3e2．设函数)(x f 在点0=x 的一个邻域内有定义，且满足2)(x x f ≤，则有（ ）．(B) （A ）)(x f 在点0=x 处不一定可导 （B ）)(x f 在点0=x 处可导，且0)0(='f （C ）)(x f 在点0=x 处可导，且0)0(≠'f （D ）)(x f 在点0=x 处取得极小值 3．设连续函数)(x f y =在区间]23[--，和]32[，上的图形分别是直径为1的上半圆周和下半圆周，在区间]02[，-和]20[，上的图形分别是直径为2的下半圆周和上半圆周（如图所示），如果⎰=xt t f x G 0d )()(，那么函数)(x G 非负的范围是（ ）． (A) （A ）整个]33[，- （B ）仅为]20[]23[，， -- （C ）仅为]30[，（D ）仅为]30[]23[，， -- 4．设函数)(x f 在区间]10[，上连续，且0)(>x f ．记⎰=101d )(x x f I ，⎰=202d )(sin πx x f I ，⎰=403d )(tan πx x f I ，则（ ）． (B)（A ）321I I I >> （B ）312I I I >> （C ）132I I I >> （D ）123I I I >>5．设函数)(x f 在区间]10[，上有连续的二阶导数，3)1(1)0(='-=f f 、，并且满足⎰=101d )(x x xf ，则=)1(f （ ）． （B ） （A ）0 （B ）1 （C ）2 （D ）3三、设211)21(-+=n n a a （ ，，，321=n ），θcos 0=a （πθ<<0），求极限)1(4lim n nn a -∞→． （本题7分） （22θ，其中nn a 2cosθ= ）四、设函数)(x f y =由方程03223323=++-y xy x 确定，且)(x f 可导，试求)(x f 的极值． （本题7分） （极大值2)2(-=f ，无极小值）五、求不定积分⎰-+21d x x x ． （本题7分）（C x x x +-++21ln 21arctan 21）六、设)(x F 是)(x f 的一个原函数，且x x f x F F 2cos )()(1)0(==，，求积分x x f d )(10⎰．（本题7分） （ )12(2-，其中x x x F cos sin )(+= ）七、求积分x x x n n d ln 10⎰，其中n 为正整数． （本题7分）（ 1)1(!)1(++-n n n n ，其中x x x n n x x x n n nn d ln 1d ln 11010-⎰⎰+-= ）八、设曲线C 与曲线：1C 22x y =和曲线：2C 2x y =的位置如图，)(y x P ，是曲线1C 上任一点，过点P 垂直于x 轴的直线与曲线C 和2C 围成图形记为A ，过点P 垂直于y 轴的直线与曲线C 和1C 围成图形记为B ．若A 和B 分别绕y 轴旋转而得到的旋转体的体积相等，求曲线C 的方程． （本题7分） （ 24x y = ） 九、设函数)(x f 满足1)1(=f ，并且对于1≥x 有)(1)(22x f x x f +='，证明)(lim x f x +∞→存在，且41)(lim π+≤+∞→x f x ． （本题7分）（ 提示：证明)(x f 单调增加有上界，用到⎰'=-x x x f f x f 1d )()1()( ）十、设函数)(x f 在区间]0[a ，上可导，且0)0(=f ，)(x f '单调增加，证明不等式⎰⎰>aax x f a x x xf 00d )(32d )(． （本题7分） （ 提示：构造函数=)(t F ⎰⎰-tt x x f t x x xf 00d )(32d )(，用单调性 ）十一、一个半径为r （1<r ）的小球嵌入一个半径为1的大球中，二球的交线恰好是一个半径为r 的圆周（如图），问当r 为何值时，位于小球内、大球为的那部分立体体积达到最大？． （本题7分）（ 52=r ，其中⎰---=11232d )1(32r y y r V ππ ）十二、设Ω是以原点和三点)110()111()010(，，、，，、，，为顶点的四面体． （1）将三重积分⎰⎰⎰Ω++z y x z y xd d de 222表示为“先z 次y 后x ”的三次积分；（2）试证明310)d e (61d d d e 2222⎰⎰⎰⎰=Ω++x z y x x z y x ． （本题7分） （⎰⎰⎰⎰⎰⎰++Ω++=11d e d d d d d e 222222xyxz y xz y xz y x z y x ，提示：后者的证明将区域101010*≤≤≤≤≤≤Ωz y x ，，：分成6个四面体，由对换性得⎰⎰⎰⎰⎰⎰Ω++Ω++=*222222d d de 61d d d e z y x z y x z y x z y x）2012年天津一中高考语文第一次模拟试题本试卷分第I卷（选择题）和第II卷（非选择题）两部分，共150分，考试时间150分钟。

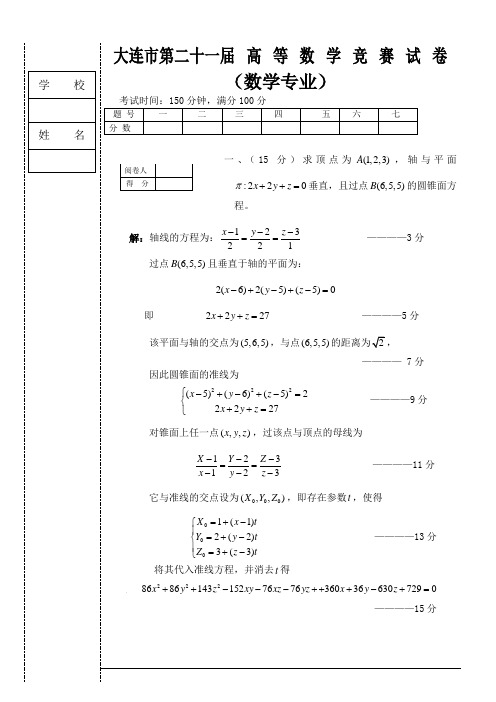
学校姓名大连市第二十一届高等数学竞赛试卷（数学专业）考试时间：150分钟，满分100分题号一二三四五六七分数一、（15分）求顶点为(1,2,3)A，轴与平面:220x y zπ++=垂直，且过点(6,5,5)B的圆锥面方程。

解：轴线的方程为：123221x y z---==————3分过点(6,5,5)B且垂直于轴的平面为：2(6)2(5)(5)0x y z-+-+-=即2227x y z++=————5分该平面与轴的交点为(5,6,5)，与点(6,5,5)的距离为2，———— 7分因此圆锥面的准线为222(5)(6)(5)22227x y zx y z⎧-+-+-=⎨++=⎩————9分对锥面上任一点(,,)x y z，过该点与顶点的母线为123123X Y Zx y z---==---————11分它与准线的交点设为000(,,)X Y Z，即存在参数t，使得1(1)2(2)3(3)X x tY y tZ z t=+-⎧⎪=+-⎨⎪=+-⎩————13分将其代入准线方程，并消去t得22286861431527676360366307290x y z xy xz yz x y z++---+++-+=————15分阅卷人得分二、（10分）设(),()f x g x 是[,]a b 上的正值连续函数，求证：存在(,)a b ξ∈，使得()()1()()baf g f x dxg x dxξξξξ-=⎰⎰。

证明： 令()()()xb x axF x e f t dt g t dt -=⎰⎰，则易知有()0,()0F a F b ==， ————5分由Rolle 中值定理知，存在(,)a b ξ∈，使得()0F ξ'=，即 ————7分()()()()()()()0b b aae f t dt g t dt f g t dt g f t dt ξξξξξξξ--+-=⎰⎰⎰⎰。

————9分化简即得结论。

2012年第四届全国大学生数学竞赛初赛（非数学类）试卷及参考答案一、简答下列各题(本题共5个小题，每题6分，共30分) 1．求极限()12lim!.n n n →∞【参考答案】：因为2211ln !!,n n n n e而211ln1ln 2ln ln !,12n n n n n且ln lim 0.n n n 所以1ln1ln 2ln lim 0.12n n n n即 21lim ln !0n n n 21lim ! 1.n n n 2．求通过直线2320,:55430x y z L x y z ⎧⎪+-+=⎪⎪⎨⎪+-+=⎪⎪⎩的两个相互垂直的平面12,ππ，使其中一个平面过点()4,3,1.-【参考答案】：过直线L 的平面束方程为 23255430x y z x y z ，即 (25)534230.x y z 若平面1 过点 4,3,1 ，代入得0 ，即 ，从而1 的方程为3410.x y z 若平面束中的平面2 与1 垂直，则 3(25)451340. 解得3, 从而平面2 的方程为2530.x y z 3．已知函数(,),ax byz u x y e+=且20ux y∂=∂∂，确定常数,a b ，使函数(,)z z x y =满足方程20.z z zz x y x y∂∂∂--+=∂∂∂∂ 【参考答案】：(,),ax by z u e au x y x x (,),ax by zu e bu x y y y2(,),ax by z u ue b a abu x y x y x y21(1)(1)(,),ax by z z z u uz e b a ab a b u x y x y x y x y若是上式等于0，只有 1(1)(1)(,)0u ub a ab a b u x y x y，由此可得 1.a b 4．设()u u x =连续可微，(2)1u =，且()()32d d Lx y u x x uu y +++⎰在右半平面上与路径无关，求().u x 【参考答案】：由32u x u x y u yx，得34x u u u ，即214dx x u du u， 这是一个一阶线性微分方程，于是由公式有通解为ln 2ln 2442uux e u edu C uudu C u uC 由(2)1u 得0C ，所以1/3.2x u5．求极限lim d .x x x t +【参考答案】：因为当1x 时，x x xxdt0x所以lim0.x xx第二题：(10分)计算20|sin |d .xe x x +∞-⎰【参考答案】：由于220(1)1|sin ||sin |nn k xxk k ex dx ex dx12(1)11sin nk k x k k e xdx应用分部积分法，有1222(1)11sin 15k k x k k e xdx e e所以有 222011|sin |15n n x k k e x dx e e212221151n e e e e 当(1)n x n 时，(1)2220|sin ||sin ||sin |n x n x x x e x dx e x dx e x dx当n ，由两边夹法则，得2222011|sin |lim |sin |.51xxxx e ex dx ex dx e【注】如果最后不用夹逼准则，而用2222011|sin |lim |sin |.51n xxn e ex dx ex dx e需要先说明20|sin |x e x dx收敛。

太阳能小屋的设计摘要本文提出了一种光伏电池“反馈式铺设”的方案，把每个问题下的铺设任务分离为几个有序的步骤来进行，步骤之间联系紧密，后一步骤的进行甚至可以反过来改变前一步骤的结果，经过多次反馈后，可以得到较优的解。

在此方案的基础上，对太阳能小屋铺设问题进入了深入的研究。

针对问题一，我们首先处理了大同市典型气象年气象数据，得到了各个表面的年辐射总量，由于各个表面的年辐射总量不一样，所以针对于各个表面的各个光伏电池的发电量、盈利额度、单位面积效益等都要分别进行计算，尤其是屋顶的情况，公示推导繁琐，数据处理起来颇为复杂，数据处理完毕后，选取候选光伏电池，建立矩形排样的模型，将各表面的非矩形约束条件转化为矩形约束来求解，铺设完成后，根据铺设的结果选取适当的光伏电池进行二次再铺设，而后将光伏电池组件进行分组，选取逆变器，调整二次再铺设后的铺设结果，使得逆变器的选取以及光伏电池组件的分组达到较佳的状态。

在问题二中，我们首先利用matlab算取了架空方式安装下的最佳倾斜角度和旋转角度，然后将架空方式安装的光伏电池进行相应的变换投影到太阳能小屋表面，根据变换后的图形利用类似问题一中提出的算法进行铺设。

在问题三中，根据题目给出的小屋建筑要求，将约束条件转化为lingo中的语言，目标函数是使得问题一中的盈利表面的面积尽可能大，房屋屋顶的倾斜角尽可能接近问题二中的最佳倾斜角。

lingo求解出的房屋尺寸在solidworks中进行三维建模，建模后的房屋进行光伏电池的铺设，根据光伏电池的铺设情况对房屋的尺寸进行小范围的调整，使得房屋的设计达到较优，即使小屋的全年发电总量尽可能大，单位发电量的费用尽可能小。

关键词：太阳能小屋光伏电池逆变器反馈式铺设最小劣度矩形排样一、问题重述在设计太阳能小屋时，需在建筑物外表面（屋顶及外墙）铺设光伏电池，光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用，并将剩余电量输入电网。

第１页 共3页2012年淮海工学院高等数学竞赛B 组试卷参考答案及评分标准1、当0x →时，1xxe 是--------------------------------------------------------------------------(D)(A) 无穷小 (B)有界但非无穷小 (C) 无穷大 (D)无界但非无穷大2、设函数22012111()(1)(2)(2012)f x xx x =--- ，则'(1)f =--------------------（C ） （A ）2012!- （B ）2011!- （C ）2011! （D ）2012!3、当0x →时，2ln(1)0()ln(1)x f x x dx +=+⎰是ln(1)20()ln(1)x g x x dx +=+⎰的----(D)(A)低价无穷小 (B)同阶非等价无穷小 (C)等价无穷小 (D)高阶无穷小 4、22(,)(0,0)(,)(0,0)limx y f xy f x y→-+存在是(,)f x y 在()0,0处可微的 ------------------ (B) (A) 必要但非充分条件 (B) 充分但非必要条件 (C) 充要条件(D) 既不充分也不必要条件5（本二学生做）、设函数)(t f 连续，则二次积分122cos ()d f r dr πθθ=⎰⎰------------（C ）（A ）22110dx⎰（B ）1220()dx x y dy +⎰（C ）2210dx dy ⎰（D ）1220()dx x y dy +⎰5（东港学生做）、设4488tan ,tan xx I dx J dx x xππππ==⎰⎰，则有---------------------（C ）（A ）ln 28I J π<<< （B ）ln 28J I π<<< （C ）ln 28I J π<<< (D)ln 28I J π<<<二、填充题（本大题共5小题，每题4分，共20分）1、22(1)1x x y x -=+的斜渐近线方程为1y x =-．2、设)(u f 可导，22(log )y f x =当自变量x 在1-=x 处取得增量0.01x ∆=-时，相应的函数增量y ∆的线性主部为0.02，则(0)f '=ln 2．提示：22222[(log )]''(log )ln 2dy f x x f x x x =∆=∆． 3、y xz x y -=+, 则n n z x ∂=∂12(1)!()n n y n x y +-+．4、21x x dx e e +∞-=+⎰4eπ．5、（本二学生做）设{}(,)|2,0,0D x y x y x y =+≤≥≥,则1d 2Dx x y σ+=++⎰⎰1. 5、（东港学生做）40=⎰2.三、计算题（本题8分）3arcsin32sin 2022lim 33x xx arc x x →--． 解：原式arcsin33arcsin33arcsin3sin 22sin 22sin 200022121lim lim lim 33131x x x x x arc x x arc x x arc x x x x ----→→→--==--------------------2(3arcsin3)ln 2(2sin 2)ln3001ln 23arcsin 3lim lim 1ln 32sin 2x x x arc x x x e x x e x arc x--→→--==----------------------2 112222'11002222ln 233(19)3ln 2(19)1lim lim ln 32ln 322(14)(14)1L Hx x x x x x --→→------==--------------------2 20293ln 227ln 22lim 42ln 38ln 32x xx →==.---------------------------------------2第２页 共3页四、计算题（本题8分） 若2arctan ln(1)sin x t y t y =⎧⎨=--⎩确定了二阶可导函数()y y x =， 试判定()y y x =在0x =处的极值性与局部凹凸性.【解】因22212'(),''()1(1)tx t x t t t -==++， 2222222(1)'()'()cos ,''()'()sin ''()cos 1(1)t t y t y t y y t y t y y t y t t --+=-=+---，----------2 则3'()1'()'()''()''()'()'(),''()[]'()'()'()'()y t d y t x t y t x t y t y x y x x t x t dt x t x t -===，------------------2 当0x =时，0t =，0y =，将其代入上述诸式，得'(0)0,''(0)10y y ==-< 则()y y x =在0x =处取得极大值(0)0y =-------------------------------------------------2 由''()y x 的连续性知，在0x =的局部邻域内''()0y x <，故其为凸的. ----------------2 五、问答题（本题10分）设数列{}{}n n x y 、满足10x >，11n x +=，1(cos )n n x x n n y x += (1,2,)n = ，请问数列{}{}n n x y 、收敛吗？若收敛，求lim ,lim n n n n x y →∞→∞；若发散，说明理由. 答：因10x >，若0n x >，则10n x +=>，{}n x 有下界----------------1于是41334(1)114n n nx C x x +>+=+,有1(1)0n n n x x x +-=+>，则{}n x 单调减少-----------------------2根据单调有界定理知{}n x 收敛，-------------------------------------------1 令lim n n x A →∞=，则0A ≥--------------------------------------------------1在11n x +=两边取极限化简得3(64)0A A A ++= 于是有lim 0n n A x →∞==， -------------------------------------------------10limlim lim (cos x n n n n n x y x e→+→∞→== ---------------------------1232003(cos 1)11ln cos cos 1limlim 221n n nn n x x n n nnnx x x x x x x x eee ++→→----== ，---------------------------2故{}n y 收敛.------------------------------------------------------1六、计算题（本题8分）如图，)2,3(是()y f x =的拐点，1l 、2l 分别是该曲线在)0,0(与)2,3(处的切线，其交点为)4,2(，设()y f x =具有三阶连续导数，求320()()x x f x dx '''+⎰．y0 2 3 4 x解： 由题设图形知， (0)0,(0)2f f '==；(3)2,(3)2,(3)0.f f f '''==-=---------2则原式3322300()()()()(21)()x x df x x x f x x df x '''''=+=+-+⎰⎰---------------233(21)()2()x f x d f x '=-++⎰-------------------------------------------------2 162[(3)(0)]ff =+-=．-----------------------------------------------------2七、计算题（本题8分）设(,)((,))((,)),((,))((,))0,z xu x y y u x y u x y x y u x y u x y ϕψϕψ=++⎧⎨''++=⎩其中),(y x z z =二阶偏导数连续，求2()xx yy xy z z z ⋅-．解：将原方程组各方程两端对x 求导得(()())1(()())0x x x z u x y u u u uy u u u ϕψϕψ''=+++=⎧⎨''''++=⎩--------2将原方程组各方程两端对y 求导得()(()())()()(()())0y y y z u x y u u u u u y u u u ϕϕψϕϕϕψ''=+++=⎧⎨'''''++=⎩---2则1()()xx x z u y u u φψ==-''''+-----------------------------------------------------------------12()(),()()yy y u z u u y u u φϕφψ''==-''''+------------------------------------------------------------1xy y z u =(),()()u y u u φφψ'=-''''+ ------------------------------------------------------------------1 故2()0xx yy xy z z z ⋅-=．---------------------------------------------------------------------------1第３页 共3页八、（该题本二学生做）计算题（本题8分）设(){}1010≤≤≤≤=y ,x x,y D ，计算{}2max d d DI x,y y x x y =-⎰⎰．解：记1:01D x y ≤≤≤，22:1D x y x ≤≤≤，： 23:01D y x ≤≤≤-------------------2则123222()d d ()d d ()d d D D D I y y xx y x y x x y x x y x y =-+-+-⎰⎰⎰⎰⎰⎰------------------22211112233d ()d d ()d d ()d xx xxx y yx y x xy x y x x xy y =-+-+-⎰⎰⎰⎰⎰⎰-------------21140=．----------------------------------------------------------2 八、（该题东港学生做）计算题（本题8分）过曲线)0y x =≥上点A 的切线与该曲线及x 轴所围区域D 的面积为43=S ，（1）求点A 的横坐标t ；（2）求D 绕直线x t =旋转一周所得旋转体的体积V ．解：（1）设(A ，则切线方程为()2313y t x t -=-，-----------------------------1 此切线与x 轴交点的横坐标为t x 20-=，-----------------------------------------------------2因401333244t S t x t =⋅==⎰，有1t =，得(11)A ,；---------------------1（2）123201333(1)d 314V ππy y π=--=⎰．-------------------------------4九、证明题（本题10分） 设0()()t F t f t dt =⎰，其中()f t 是周期为T 的连续函数，证明：（1）()()()F t T F t F T +=+；（2）0()[()()]()tg t F t T F t dt TF t =+--⎰是周期为T 的周期函数．证明：（1）设()()()()HtFt T Ft FT =+----------------------------------------------------1因()f t 是周期为T 的连续函数，则'()()()0H t f t T f t =+-=-------------------------2 于是()(0)(0)0H t C H F ====，则（1）得证；--------------------------------------------1 （2）由上，知0()()()()()t g t F T dt TF t tF T TF t =-=-⎰---------------------------------1则'()()()g t F T Tf t =----------------------------------------------------------------------------1 令()()()G t g t T g t =+-，则'()'()'()0G t g t T g t =+-=-------------------------------2 于是()(0)()(0)0G t C G g T g ===-=,故（2）得证．------------------------------------1十、应用题（本题10分）设圆222x y y +=含于椭圆22221x y a b+=的内部, 且圆与椭圆相切于两点(即在这两点处圆与椭圆都有公共切线)，（1）求,a b 满足的等式；（2） 求,a b 的值, 使椭圆的面积最小．解：（1） 由题意，圆与椭圆的公切点00(,)x y 不在y 轴上，则00x ≠，--------------1同时220000()(1)b x a y x y -=--，即2220)y b b a =---------------------------------1 因22220000222,1x y x y y a b +=+=，有222200220b a y y a b--+=----------------------------1 将上述两式消0y ，得22420ab a b --=；-----------------------------------------------------1（2） 按题意, 需求椭圆面积S ab π=在条件22420a b a b --=下的最小值，构造拉格朗日函数2242()L ab a b a b πλ=+-- ------------------------------------------1 令2222(2)0,2(1)0a b L b a b a L a b a πλπλ=+-==+-=-----------------------------2 可得242b a =，代入22420a b a b --=，得(,)(a b =，-----------------2 因该实际问题中,椭圆面积的最小值存在, 则上述坐标即为所求．------------------------1。

2012年浙江省高等数学（微积分）竞赛试题 工科类 一：计算题（每小题14分，共70分）1：计算：()+lim log +a ba n x x →∞2设函数f ：R R →可导，且,x y R ∀∈，满足：()()+++f x y f x y xy ≥，求()f x 的表达式。

3计算： 0sin ,n x xdx n Z π*∈⎰4计算：{}-min ,2Dx y x y dxdy ⎰⎰，其中D 是2=y x 和2=x y 所围成的封闭区域。

5求曲线{33=cos =sin x a y a θθ()0,>0a θπ≤≤的形心。

二：（本题满分20分）证明：=111+ln <<1+ln ,ni n n n Z n i *∈∑三：（本题满分20分）设2:u RR →，且u 具有二阶连续偏导，求证当u 可以表示成：()()(),=u x y f x f y 的充分必要条件是：2=u u uu x y y y∂∂∂∂∂∂∂ 。

四：（本题满分20分）在空旷的草地上有一个地面半径为3的圆柱体，在墙角栓有一头山羊，其绳长为π，求山羊能吃到草地的面积。

五：（本题满分20分）求证：()-1=1=111-1C =,k nn k nk k n Z k k*∈∑∑参考答案一、计算题1、若a b ≥ l i m l o g(a bx x x x →+∞+l i m l o g(1)l i m l o g (1a b ab ax xx x x x a x a --→+∞→+∞=+=++= 同理，当a b <时，lim log ()a b x x x x →+∞+b =， 所以lim log ()a bx x x x →+∞+max(,)a b =2、解：由假设，0y ∀>，有()()1f x y f x x y+-≥+ f 可导()1f x x +'⇒≥+同理()1()1f x x f x x -''≤+⇒=+ 2()/2f x x x c =++ 3、解：sin d n x x x π⎰()011sin sin nnj j j j x x dx x j xdx ππππππ-====+-∑∑⎰⎰()()201sin d 21212nj n x x x j n n n n n n πππππ==+-=++-=+∑⎰4、解：(){}(){}12,1,,/2,01/2D x y x y x D x y x y x x =≤≤≤≤=≤≤≤≤(){}(){}2234,,1/21,,/2,01/2D x y xy x x D x y xy x x =≤≤≤≤=≤≤≤≤原积分12()d d ()d d D D y x x x y x y x x y =-+-⎰⎰⎰⎰34()d d ()d d D D x y x x y x y y x y +-+-⎰⎰⎰⎰211102d )d d ()d xxxx y x x y x x y x y =-+-⎰⎰⎰21112221002d ()d d ()2d xx xx x y x x y x x y y y +-+-⎰⎰⎰⎰11341456142210021211111()678851232x x x x x x x =-++-++146720112()24621x x x +-+111124724532245=++⨯⨯⨯⨯112533216642117920++=⨯⨯ 5、解：/0c LLx xds ds ==⎰⎰，d /d c LLy y s s =⎰⎰而d 3sin cos d s a θθθθ== 2d 3sin cos d sin cos 3Ls a ba d a ππθθθθθθ/===⎰⎰⎰/2324206d sin 3sin cos d 6sin cos d 5Ly s a x a a a ππθθθθθθθ===⎰⎰⎰0c x ∴= 25c y a =二、证明：显然11111d d j j jj x x x jx +-<<⎰⎰ 2j ≥1 1122111111d 1d 1ln nn n j n j j j j x x n j j x x -===∴=+<+=+=+∑∑∑⎰⎰另一方面111111111111d ln nn n j j j j j x n j jn x n n --+====+>+=+∑∑∑⎰三、证明：()()u f x g y =时，显然有xy x y uu u u = 反之，若xy x y uu u u =成立，即有2()/()0xxy x y y u uu u u u u-== 1/()x u u f x ⇒= 也即1121ln ()d ()()()u f x x g y f x g y =+=+⎰ ()()u f x g y ∴=四、解：(方法一)以圆柱形旁子的圆心为原点，拴羊点在x 轴上3x =点，则羊跑最远的曲线在3x <的区域内是渐开线 即 3(cos (/3)sin )x t t t π=-- 3(sin (/3)cos )y t t t π=+- 记在3x <山羊能吃到草的草地面积为1S3/30213/2/32d 29sin d 2(3sin (3)cos )(3)cos d S y x t t t t t t t t ππππ=-=+--⎰⎰⎰/32029sin d t t π-⎰/32223(3)sin cos (3)cos d t t t t t t πππ⎡⎤=-+-⎣⎦⎰/32029sin d t t π-⎰/322013(3)sin (3)(sin 2)2t t t t t πππ⎡⎤=-+-+⎢⎥⎣⎦/32016(3)(sin 2)9sin d 2t t t t t ππ⎡⎤+-+-⎢⎥⎣⎦⎰()/3/3/322000191133cos 2sin 29cos 2d 2222t t t t t t t t ππππ⎛⎫⎛⎫⎛⎫=----+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰33/319sin 2349t t ππ⎛⎫=+-=⎪⎝⎭所以山羊能吃到草的草地面积333119218S πππ=+= (方法二) 山羊能吃到草的草地面积S 可表示为一半圆与绳子绕向房子所能到达的面积1S 和 绳子绕向房子时转过θ∆ 其扫过的面积可近似为扇形22r θ∆()2/33103/9S d ππθθπ=-=⎰所以311/18S π=五、证明：111110011111(1)(1)d (1)d nn n k k k k k k k knn n k k k C C t t C t t k t ---===--=-=-∑∑∑⎰⎰ 1100(1)11(1)d d n n t t t t t t ----==⎰⎰101d 1nx x x -=-⎰ 而11100111d d 1nnn k k k t t t t k t -==1-==-∑∑⎰⎰ ∴等式成立。

2012年天津市大学数学竞赛试题（经管类）一、填空题（共15分，每空3分）1．设1e 12sin )(1)(3--+=x x x f x f ，则极限=→)(lim 0x f n ． （ 6 ）2．设函数)(x f 连续切不等于0，又⎰+=C x x x xf arcsin d )(，则=⎰)(d x f x． （ C x +--232)1(31 ）3．半径为R 的无盖半球形容器中装满了水，然后慢慢地使其倾斜3π，则流出的水量=V ． （3833R π ） 4．设函数)(x f 可微，且1)0(0)0(='=f f ，，又设平面区域222t y x D ≤+：，则=+⎰⎰+→σd )(1lim 223Dt y x f t ． （32π ） 5．设函数)(x f 在点0=x 处二阶可导，且2cos 1)(lim0=-→xx f x ，则='')0(f ．（ 2 ） 二、单项选择题（共15分，每空3分）1．设函数)(x f 有连续导数，3)0(1)0(='=f f ，，则极限=→xx x f 21)]([lim （ ）．(D)（A ）1 （B ）e （C ）3/2e（D ）2/3e2．设函数)(x f 在点0=x 的一个邻域内有定义，且满足2)(x x f ≤，则有（ ）．(B) （A ）)(x f 在点0=x 处不一定可导 （B ）)(x f 在点0=x 处可导，且0)0(='f （C ）)(x f 在点0=x 处可导，且0)0(≠'f （D ）)(x f 在点0=x 处取得极小值 3．设连续函数)(x f y =在区间]23[--，和]32[，上的图形分别是直径为1的上半圆周和下半圆周，在区间]02[，-和]20[，上的图形分别是直径为2的下半圆周和上半圆周（如图所示），如果⎰=xt t f x G 0d )()(，那么函数)(x G 非负的范围是（ ）． (A) （A ）整个]33[，- （B ）仅为]20[]23[，，Y -- （C ）仅为]30[，（D ）仅为]30[]23[，，Y -- 4．设函数)(x f 在区间]10[，上连续，且0)(>x f ．记⎰=101d )(x x f I ，⎰=202d )(sin πx x f I ，⎰=403d )(tan πx x f I ，则（ ）． (B)（A ）321I I I >> （B ）312I I I >> （C ）132I I I >> （D ）123I I I >>5．设函数)(x f 在区间]10[，上有连续的二阶导数，3)1(1)0(='-=f f 、，并且满足⎰=101d )(x x xf ，则=)1(f （ ）． （B ） （A ）0 （B ）1 （C ）2 （D ）3三、设211)21(-+=n n a a （Λ，，，321=n ），θcos 0=a （πθ<<0），求极限)1(4lim n nn a -∞→． （本题7分） （22θ，其中nn a 2cosθ= ）四、设函数)(x f y =由方程03223323=++-y xy x 确定，且)(x f 可导，试求)(x f 的极值． （本题7分） （极大值2)2(-=f ，无极小值）五、求不定积分⎰-+21d x x x ． （本题7分）（C x x x +-++21ln 21arctan 21）六、设)(x F 是)(x f 的一个原函数，且x x f x F F 2cos )()(1)0(==，，求积分x x f d )(10⎰．（本题7分） （ )12(2-，其中x x x F cos sin )(+= ）七、求积分x x x n n d ln 10⎰，其中n 为正整数． （本题7分）（ 1)1(!)1(++-n n n n ，其中x x x n n x x x n n nn d ln 1d ln 11010-⎰⎰+-= ）八、设曲线C 与曲线：1C 22x y =和曲线：2C 2x y =的位置如图，)(y x P ，是曲线1C 上任一点，过点P 垂直于x 轴的直线与曲线C 和2C 围成图形记为A ，过点P 垂直于y 轴的直线与曲线C 和1C 围成图形记为B ．若A 和B 分别绕y 轴旋转而得到的旋转体的体积相等，求曲线C 的方程． （本题7分） （ 24x y = ） 九、设函数)(x f 满足1)1(=f ，并且对于1≥x 有)(1)(22x f x x f +='，证明)(lim x f x +∞→存在，且41)(lim π+≤+∞→x f x ． （本题7分）（ 提示：证明)(x f 单调增加有上界，用到⎰'=-x x x f f x f 1d )()1()( ）十、设函数)(x f 在区间]0[a ，上可导，且0)0(=f ，)(x f '单调增加，证明不等式⎰⎰>aax x f a x x xf 00d )(32d )(． （本题7分） （ 提示：构造函数=)(t F ⎰⎰-tt x x f t x x xf 00d )(32d )(，用单调性 ）十一、一个半径为r （1<r ）的小球嵌入一个半径为1的大球中，二球的交线恰好是一个半径为r 的圆周（如图），问当r 为何值时，位于小球内、大球为的那部分立体体积达到最大？． （本题7分）（ 52=r ，其中⎰---=11232d )1(32r y y r V ππ ）十二、设Ω是以原点和三点)110()111()010(，，、，，、，，为顶点的四面体． （1）将三重积分⎰⎰⎰Ω++z y x z y xd d de 222表示为“先z 次y 后x ”的三次积分；（2）试证明310)d e (61d d d e 2222⎰⎰⎰⎰=Ω++x z y x x z y x ． （本题7分） （⎰⎰⎰⎰⎰⎰++Ω++=11d e d d d d d e 222222xyxz y xz y xz y x z y x ，提示：后者的证明将区域101010*≤≤≤≤≤≤Ωz y x ，，：分成6个四面体，由对换性得⎰⎰⎰⎰⎰⎰Ω++Ω++=*222222d d de 61d d d e z y x z y x z y x z y x）。

一．（15分）设有空间中五点: ()()()()()1,0,1,1,1,2,1,1,2,3,1,0,3,1,2A B C D E --.试求过点E 且与,,A B C 所在平面∑平行而与直线AD 垂直的直线方程.二．（15分）设()f x 在[],a b 上有两阶导数, 且()f x ''在上黎曼可积, 证明()()()()()()[],,.xa f x f a f a x a x t f t dt x ab '''=+-+-∀∈⎰ 三．（10分）设01n k k k <<< 为给定的正整数,12,,n A A A 为实参数. 指出函数()011sin sin sin n n f x k x A k x A k x =+++ 在[)0,2π上零点个数的（当12,,n A A A 变化时的）最小可能值并加以证明.四．（10分）设正数列n a满足lim 1,lim ,lim1n n n n n a a →+∞→+∞=<+∞. 求证:12lim1n n a a a n →+∞+++= . 五．（15分）设,A B 分别是32⨯和23⨯实矩阵, 若8043962201AB -⎛⎫ ⎪ ⎪=-- ⎪ ⎪-⎝⎭. 求BA . 六．（20分）设{}{},i i i I i I A B ∈∈是数域F 上两个矩阵集合, 称它们在F 上相似: 如果存在F上与i I ∈无关的可逆矩阵P 使得1,ii P AP B i I -=∀∈. 证明: 有理数域Q 上两个矩阵集合{}{},i i i I i I A B ∈∈, 如果它们在实数域R 上相似, 则它们在有理数域Q 上也相似.七．（15分）设()(),F x G x 是[)0,+∞上的两个非负单调递减函数, ()()()lim 0.x x F x G x →+∞+=(1)证明: ()0,lim cos 0x xF xt tdt εε+∞→+∞∀>=⎰. (2)若进一步有()()()0limcos 0x t F t G t dt n +∞→+∞-=⎰. 证明: ()()()()00limcos 0x F t G t xt dt +∞→-=⎰.。