九年级数学二次根式的加减同步练习

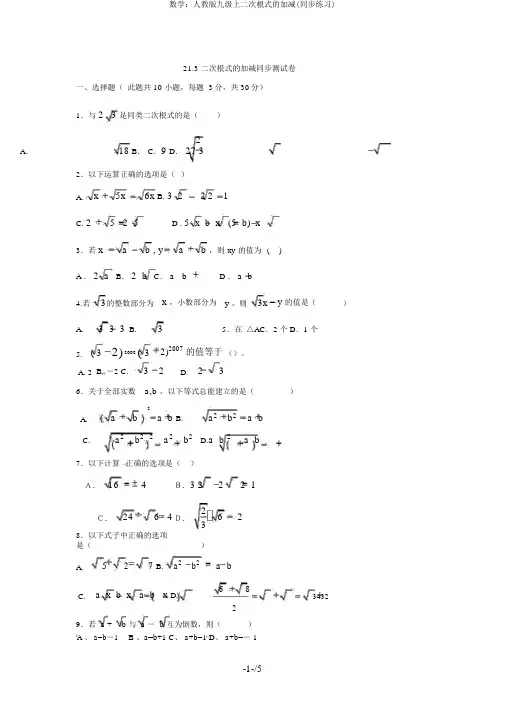
21.3 二次根式的加减同步测试卷一、选择题（此题共 10 小题，每题 3分，共 30分）1．与2 3 是同类二次根式的是（）2A．18 B．C．9 D． 27 32．以下运算正确的选项是（）A.x5x6xB. 3 2221C. 2 5 2 5 D . 5 x b x (5 b) x3．若x a b , y a b ，则xy的值为()A ．2 a B．2 b C．a b D ．a b4.若3的整数部分为x ，小数部分为y ，则3x y 的值是（）A. 3 3 3B.35．在△AC．2 个 D．1 个5.(32) 2008 (32)2007的值等于（）A. 2B. －2C.32D.236．关于全部实数a,b ，以下等式总能建立的是（）a 2a b B.a2b2 a bA.bC.a2 b2 2 a2 b2D.a b 2 a b 7．以下计算正确的选项是（）Ａ． 164Ｂ．3 22 2 1Ｃ．24 6 4Ｄ．262 38．以下式子中正确的选项是（）A.527B.a2 b2 a bC. a x b x a b xD.683432 29．若 a + b 与 a － b 互为倒数，则（）A 、 a=b－1 B 、a=b+1 C、 a+b=1 D、 a+b=－ 110．以下计算错误的是 ()．．(A) 1477 2(B)60523(C)9a25a8a(D) 3223二、填空题（此题共 8小题，每题 4 分，共 32 分）11．若最简二次根式 a 1 2a 5 与3b4a 是同类二次根式，则 a ____, b ____ 12．在8,12, 18, 20 中，与 2 是同类二次根式的是。

13． 5－ 5 的整数部分是_________14．计算：12 3 315．方程2（ x－ 1）＝ x＋ 1 的解是 ____________．x1x15x 的值等于。

16．已知 2 ，则17 ．如图，矩形内两相邻正方形的面积分别是 2 和 6 ，那么矩形内暗影部分的面积是．（结果可用根号表示）2618．图 7 是由边长为1m 的正方形地砖铺设的地面表示图，小明沿图中所示的折线从A→B →C 所走的行程为_______m．（结果保存根号）A1mBC图 7三、解答题（此题共 8小题，共58分）1 a 3 a37a512a719．（ 1）248a4a(4b a1 a 3b) (3a b9ab )( b0)（2）b a a20．一个直角三角形的两条直角边长分别是(3 2 )cm, (32 )cm,求这个三角形的面积和周长21．（1）3 8 ( 54 5 2 2 6)（2）(3 2 5 3)(3 2 53)(13)2（3）23x y9 y 6y是同类根式，求22．已知最简根式5x 2和23．化简（53 2 ）（53 2 ）24．已知菱形 ABCD的对角线 AC＝274,BD 2 725．先化简，再求值：x 252x3，此中 xx x2x， y 的值4，求菱形的边长和面积。

21.3二次根式的加减同步测试卷一、选择题（本题共10小题，每题3分，共30分）1．与 ）A B CD ． 2．下列运算正确的是（ ） A.x x x 65=+B .12223=-C .5252=+D .x b x b x )5(5-=-3．若b a y b a x +=-=,，则xy 的值为 ( )A ．a 2B ．b 2C ．b a +D ．b a -4.x ，小数部分为y y -的值是（）A. 35．在△A C ．2个 D ．1个 5. 的值等于20072008)23()23(+-（） A. 2B. －2C. 23-D. 32-6．对于所有实数,a b ，下列等式总能成立的是（ ）A. 2a b =+a b =+22a b =+a b =+7．下列计算正确的是（ ）4=± Ｂ．1=4= 623=8．下列式子中正确的是（ ）= B. a b =-C. (a b =-2==9．若 a + b 与 a － b 互为倒数，则（ ）A 、a=b －1B 、a=b+1C 、a+b=1D 、a+b=－110．下列计算错误．．的是( )==(D)3二、填空题（本题共8小题，每题4分，共32分）11．若最简二次根式____,____a b ==12是同类二次根式的是。

13．5的整数部分是_________14=15．方程2（x －1）＝x ＋1的解是____________．16．已知251-=x ，则x x 1-的值等于。

17．如图，矩形内两相邻正方形的面积分别是2和6，那么矩形内阴影部分的面积18．图7A →B →C 所走的路程为_______m ．（结果保留根号）三、解答题（本题共8小题，共58分）19．（1）123478143527a a a a a a +-- （2）()()()413903b a b a a b a b a ab b +-+> 20．一个直角三角形的两条直角边长分别是,cm )23(,cm )23(+-求这个三角形的面积图7和周长21．（1）38545226⨯--()（2）()()32533253+-（3）()-+1322 22．已知最简根式y 9y x 3y 62x 5-+--和是同类根式，求x ，y 的值23．化简（235+-）（235--）24．已知菱形ABCD 的对角线AC ＝472,472-=+BD ，求菱形的边长和面积。

九年级数学二次根式的加减测试题想要学好数学，一定要多做同步练习，以下所介绍的九年级数学二次根式的加减测试题同步练习，主要是针对每一单元学过的知识来巩固自己所学过的内容，希望对大家有所帮助!【模拟试题】(答题时间：30分钟)一. 选择题：1. 化简得( )A. (a-1)B. (1-a)C. -(a+1)D. (a-1)2. 计算( )A. B. 3 C. - D. -3. 设x= ，则x与y的大小关系为( )A. xyB. x=yC. x二. 填空：4. 下列二次根式：①②③④⑤其中为非最简二次根式的有(在横线上写题号) ，与是同类二次根式的有(写题号)5. 合并同类二次根式。

6. 已知。

三. 解答题：7. 已知。

8. 计算：(1)(2)(3)(4)(5)9. 条件求值：(1)已知：。

(2)已知：的值。

(3)已知：。

10. 已知菱形ABCD的对角线AC= ，求菱形的边长和面积。

【试题答案】1. B2. A3. A4. ②,③,④①,②,③,④5. 06. 257.解：原式结果为-2-8. (1)原式=(2)原式=(3)-2 (4)0 (5)39. (1)x+1当(2)解：∵两边平方得x2-4x+1=0(3)解：∵，，4x2-4x-1=0=1家庭是幼儿语言活动的重要环境，为了与家长配合做好幼儿阅读训练工作，孩子一入园就召开家长会，给家长提出早期抓好幼儿阅读的要求。

我把幼儿在园里的阅读活动及阅读情况及时传递给家长，要求孩子回家向家长朗诵儿歌，表演故事。

我和家长共同配合，一道训练，幼儿的阅读能力提高很快。

10. 解：(菱形的边长)2=“师”之概念，大体是从先秦时期的“师长、师傅、先生”而来。

其中“师傅”更早则意指春秋时国君的老师。

《说文解字》中有注曰：“师教人以道者之称也”。

“师”之含义，现在泛指从事教育工作或是传授知识技术也或是某方面有特长值得学习者。

“老师”的原意并非由“老”而形容“师”。

“老”在旧语义中也是一种尊称，隐喻年长且学识渊博者。

典型例题一例01．在下列二次根式中，与b a +是同类二次根式是（ ）A ．3)(52b a +B ．)(231b a + C ．4)(1b a b a ++ D ．b a +3 分析 因3)(52b a +=b a b a ++)(52， b a b a +=+32)(231， ⋅++=++=++=++)(313),()(1)(124b a ba b a b a b a b a b a b a 故只有A 的二次根式与b a +被开方数完全相同. 是同类二次根式.解答 A说明 判断是否为同类二次根式，必须先化成最简二次根式.典型例题二例02．下列算式中，正确的是（ ）A ．333n m n m -=-B ．ab b a 835=+C ．1037=+x xD ．52523521=+ 分析 3)(33n m n m -=-，n m -应添上括号，所以A 是错的. B 中a 5，b 3不是同类二次根式，不能合并. x x x 1037=+. 故C 也是错的.解答 D说明 二次根式相加减，就是合并同类二次根式，与整式加减类似.典型例题三例03．计算：)315.125.4()5.248116(+---分析 先将题目中的每个二项根式化简，为此要把被开方数中的带分数和小数化假分数，为二次根式的化简创造有利条件.解答 )315.125.4()5.248116(+--- 33125222322722931215213217212363122529249896-+--=-+--⨯=-+--= 331223312)25232729(-=-+--= 说明 本题源于课本中的有关计算题，可以再适当变换题目中的被开方数、正负号，增加括号等，都不涉及课本的实质. 对这样的题目，要能熟练地进行运算.典型例题四例04．已知最简根式)23(34+-+a b a 和)62(4+--+b a b 是同类根式，求2)2(b a +的值. 分析 由同类根式的定义可知，根指数相同，可得到关于a ，b 的二元方程组. 解答 由同类根式的定义可知⎩⎨⎧+=++--=+-434)62()23(b b a b a a 解⎩⎨⎧=-=62b a ∴10010)622()2(222==⋅+-=+b a 典型例题五例05．化简：（1）725341874321a a a a a a --+（2）xxy x x xy x 14434114831434+-- （3）x x x x x x x 1082363273223-+-（4）)0(22>>++--+b a ba ab b a a b 解答 （1）原式=a aa a a a a a a 2324874321--+ a a a a a a a a a a 83214874321-=--+=（2）原式=x xxy x x x x y x 42123411334+--x y y x x y y x )1112(338)1112(3)434(2424-+-=-+-= （3）原式=x x x x x x x x x 362336333322⋅-+-⋅ 03)322(3332332=-+-=-+-=x x x x x xx x x x x x x（4）∵0>>b a ，∴10<<a b ，1>ba ba ab b a a b <<<∴,0 ∴原式=22++--+b a a b b a a bab ab aba ab a b b a b a a b b a a b b a a b b a a b 22)()()(22-=-=+--=+--=+--= 说明 利用二次根式的性质来化简.典型例题六例06．计算：（1）1477175483+- （2）a a a a a 235425-+（3）)20125.02()3155.03(--- 解答 （1）1477175483+- 38335343=+-⨯= （2）a a a a a 235425-+a a aa a a a a 2222845=-+=（3）)20125.02()3155.03(--- 52335252221335223+-=+--=说明 二次根式的加减，首先是化简，即把每一个二次根式都化为最简二次根式. 在化简后，就是类似整式加减的运算了. 整式加减无非是去括号，合并同类项. 二次根式的加减在化简后也是这样，同类二次根式类似于同类项，加法的运算律同样适用. 合并同类二次根式，相当于合并它们的“系数”.防止产生的错误有：①没有化成最简二次根式. 如题（1）错为12248=；②不同类根式的错误合并，如题（3）错为3与2合并为5；③表达不正确，如223. 根号前的分数应写成假分数，不应写成带分数.典型例题七例07．设32,32-=-+=-c b b a ，求ac bc ab c b a ---++222的值. 解答 因32+=-b a ，32-=-c b ， 故4)32(32)()(=-++=-+-=-c b b a c a又因ac bc ab c b a ---++222 .153021]4)32()32[(21])()()[(21)222222(21222222222=⨯=+-++=-+-+-=---++=c a c b b a ac bc ab c b a 说明 在解代数式的化简和求值问题时，对条件、结论往往需要变形. 请注意以下两个常见的变形.（1）])()()[(212222c a c b b a ac bc ab c -+-+-=--- （2）))((3222333ac bc ab c b a c b a abc c b a ---++++=-++习题精选之填空题（1）______2008275=-+；（2）______80453202=+-；（3）______24327482=++；（4）______1085124755=--；（5）______6148252294=+-； （6）______216216524354=++-； （7）______216312454600=--+； （8）______5.1281132=+-；（9）______125.045.022.05=+-； （10）______22121423=-+． 参考答案： （1）2635-；（2）5-；（3）320；（4）313-；（5）76615-；（6）65；（7）69；（8）2423；（9）5；（10）229 选择题1．选择题（1）下列各组根式中是同类二次根式的是（ ）（A ）ab 与2ab （B ）mn 与nm 11+ （C ）22n m +与22n m - （D ）4398b a 与2943b a （2）下列各式中与271是同类二次根式的是（ ） （A ）18 （B ）12 （C ）32 （D ）92 （3）下列各式中与b a 3不是同类二次根式的是（ ）（A ）4ab （B ）a b （C ）22b a （D ）ab1 （4）下列二次根式中与yx 不是同类二次根式的是（ ）（A ）2xy （B ）y x 3 （C ）xy1 （D ）3x y （5）二次根式①5.03，②315，③125.02，④20中是同类二次根式的是（ ） （A ）②和③ （B ）③和④ （C ）①和③ （D ）①和④（6）下列各组二次式中，可化为同类二次根式的是（ ）（A ）2a 和23a （B ）x x 2和xx 12 （C ）x 2和x 3 （D ）33a 和43a（7）在二次根式b a 3，2ab ，a b ，ab1，22b a 中，是同类二次根式的个数为（ ）（A ）2 （B ）3 （C ）4 （D ）52．选择题（1）下列二次根式中，是同类二次根式的是（ ） ①b a 34，②a b a 423，③232b a ，④b a b 2 （A ）①② （B ）②④ （C ）①② ④ （D ）①③④（2）化简xx x x 2118612-得（ ） （A ）x x x x 23- （B ）x x x 2212-（C ）x x 22 （D ）0（3）下列命题中正确的是（ ）（A ）3a 和a1是同类二次根式 （B ）a 2与a 2是同类二次根式（C ）被开方数完全相同的二次根式不一定是同类二次根式（D ）a1与a 不是同类二次根式 （4）下列根式中与8是同类二次根式的是（ ）（A ）2 （B ）3 （C ）5 （D ）6（5）下列各组式子中，不是同类二次根式的是（ ）（A ）181与18 （B ）63与281- （C ）48与8.4 （D ）125.0与128（6）与a 27是同类二次根式的是（ ）（A ）a 54 （B ）a 121- （C ）31a （D ）482a 3．选择题（1）下列式子中，是同类二次根式的一组是（ ）（A ）36.0与6.02 （B ）b a 33与22ab（C ）22b a -与2221b a + （D ）c b a b a 53与acb b a 24 （2）下列计算中，化简正确的一组是（ ）（A ）1073=+ （B ）a a a 32=+（C ）x y x x y x x x y xx 1)(1112+=+=+ （D ）b aa b a b a a b b a 221622123218222-=-=- （3）下列说法正确的是（ ）（A ）被开方数不同的二次根式一定不是同类二次根式（B ）a 2与a 2是同类二次根式（C ）a1与a 不是同类二次根式 （D ）被开方数完全相同的二次根式是同类二次根式（4）当2523<<x 时，化简961222+-++-x x x x 得（ ） （A ）x 2 （B ）2 （C ）2- （D ）x 2-参考答案：1．（1）D （2）B （3）C （4）A （5）C （6）B （7）B2．（1）C （2）D （3）A （4）A （5）C （6）B3．（1）D （2）D （3）D （4）B判断题1．判断下列各组二次根式是不是同类二次根式（1）543和245 （2）7521和2713 （3）3241和5.0 （4）32x 与x21 （5）39a a 与533a （6）175-与631 （7）b a 3，a b 3与b a （8）c ab 5161，27bc a 与54ab c 2．下列各式中，哪些是同类二次根式？ ①312，②2712，③a b -，④84，⑤21.0-⑥75.0，⑦b a a b ，⑧ab 1，⑨108，⑩531b a a 3．判断题（1）2222=+（ ）（2）x b a x b x a -=-（ ）（3）ab b a 752=+（ ）（4）x x x 353332=+（ ）（5）235=-a a （ ）（6）x b a x b x a )(-=- （ ）（7）83与61不是同类二次根式 （ ） （8）3a 、2ab 与a 1不是同类二次根式 （ ） （9）33a 与a 是同类二次根式 （ ）（10）272、6与54是同类二次根式 （ ）参考答案：1．（1）是 （2）是 （3）是 （4）是 （5）不是 （6）是 （7）是 （8）不是2．①④⑤是同类二次根式，②⑥⑨是同类二次根式，③⑦⑧⑩是同类二次根式.3．（1）×（2）×（3）×（4）√（5）×（6）√（7）×（8）×（9）×（10）√ 解答题1．合并同类二次根式（1）3218121-+ （2）32222133123+-+-（3）4832315311312--+ （4）2001286175.142112+-+ （5）xx x x x x 12964212-+ （6）b a b a 9735+--（7）32518283+-（8）3417343731--+ （9）b a b a 128275186-+- （10）c a c ab ab c a ab a 333328534321123636-+-2．计算题（1）32128-++ （2）192214721- （3）5018283-+ （4）3004875-+（5）8200242+- （6）1509654-+（7）312316+- （8）10210005240+- 3．计算题 （1）5.050182183+-+（2）212525401000-+- （3）)40551736516(633++- （4）32935148x x x x x x x +-- （5）91114275444328+-- （6）4135941125221300+-- 4．计算题（1）)75315(27+- （2）)9921765(44-- （3）)5145354(203++-参考答案：1．（1）285 （2）332223+ （3）0 （4）73522051+ （5）x x （6）a b 26-（7）220 （8）732321- （9）b a 3725- （10）ac ac ab ab 722732-2．（1）323+ （2）3225-（3）27 （4）3- （5）23 （6）62 （7）3 （8）03．（1）23 （2）10217 （3）55137757- （4）x x - （5）1135 （6）13294．（1）3310-（2）1112- （3）5536- 解答题1．已知长方形长为a ，宽为b ，求与下列长方形面积相等的正方形的边长x ：（1）8,49==b a （2）8.0,6.3==b a（3）12513,532==b a （4）m b m a 641,41== 2．计算题（1）)323485()5012739(---+（2）)132331242()4882(+-+ （3）)1881()3122112(--+-（4）)300512732()162912(---3．计算题 （1）a a a a a 235425-+ （2）5343581b bb b b +- （3）mm m m m m 12964212-+ 4．求值：已知2,3==y x ，求y x x xy y x xy x 2252353312+--的值.参考答案：1．（1）214 （2）256 （3）2513 （4）16m 2．（1）2733+ （2）3327-- （3）249338+ （4）0 3．（1）a a 28 （2）b b 10 （3）m m4．（1）3645353)(22-=+--y x x y x解答题1．计算题（1）187825-+ （2）101252403-- （3）232282xy x x +- （4）)2775298(18+--2．已知直角三角形的两条直角边为a 、b 、c 为斜边，且27=a ，275=c ，求这个直角三角形的周长.3．证明：已知ABC Rt ∆中，斜边为c ，直角边长a 、b ，求证：b c a c a c a c a c 2=+-+-+.参考答案：1．（1）214- （2）10528 （3）x y x 2)221(+- （4）2437- 2．218318+〔提示：21822=-=a c b 〕3．提示：等式左边a c a c a c a c +-+-+=22a c a c a c --++=222ac c -=b c 2==右边。

21.3 二次根式的加减5分钟训练(预习类训练,可用于课前)1.把下列二次根式化为最简二次根式: (1)48；(2)y x 275.解：(1)48=342⨯=43. (2)y x 275=y y 3522∙=5x y 3.2.如何进行二次根式加减运算? 思路分析：根据二次根式加减运算法则进行回答.解：二次根式加减运算时,可以先将二次根式化成最简二次根式，再将被开方数相同的二次根式进行合并.3.计算：28-63. 解：6328-=27-37=(2-3)7=-7. 4.计算：2(2-1).思路分析：根据整式乘法法则进行计算. 解：2(2-1)=2·2-2·1=2-2.10分钟训练(强化类训练,可用于课中)1.下列根式，不能与48合并的是( ) A.12.0 B.18 C.311 D.-75 思路解析：将二次根式化成最简二次根式后，若被开方数相同才能合并.48=43,3511001212.0==,18=32,33234311==,-75=-53. 答案：B2.(江苏徐州模拟)下列运算中错误的是( ) A.2×3=6 B.21=22 C.22+32=52 D.2)32(-=2-3思路解析：此题考查二次根式的乘除、加减及化简,选项A 、B 、C 都符合各运算法则,而D 中由于2<3,所以结果应为3-2.答案：D3.化简8-2(2+2)得( )A.-2B.2-2C.2D.42-2思路解析：先利用整式的运算法则进行化简.8-2(2+2)=22-2-22=-2.答案：A4.(经典回放)如果最简二次根式83-a 与a 217-是同类根式(最简形式被开方数相同的二次根式),那么使x a 24-有意义的x 的取值范围是( )A.x≤10B.x≥10C.x<10D.x>10思路解析:此题考查最简二次根式、同类二次根式的定义以及一元一次方程、一元一次不等式的解法和二次根式的定义.此题的综合性较强,涉及到的知识点很多.首先根据同类二次根式的定义和最简二次根式的定义得到一元一次方程,然后把所求得的解代入x a 24-,再根据二次根式的定义得不等式,解之即得答案A.解此题时注意两点:①二次根式的被开方数要大于或等于0;②解不等式时要注意不等号方向的改变. 答案:A5.计算：(1)318+5150-421; (2)(5+26)(26-5). 思路分析：(1)二次根式加减运算时,可以先将二次根式化成最简二次根式，再将被开方数相同的二次根式进行合并;(2)利用乘法公式进行计算.解：(1)318+5150-421=92+2-22=(9+1-2)2=82. (2)(5+26)(26-5)=(26)2-52=24-25=-1.快乐时光什么是赤壁之战?学生:“老师,什么是赤壁之战?”老师:“赤臂嘛,就是光着膀子,赤壁之战,自然就是光着膀子打仗了.”30分钟训练(巩固类训练,可用于课后)1.下列各式正确的是( ) A.2232+=2+3 B.32+53=(3+5)23 C.221215-=1215+·1215- D.214=221 思路解析：判断是否正确,要看化简的过程是否符合运算法则.13943222=+=+, 32与53不能合并,214=29=223. 答案：C2.已知x=3-2,那么x+x1的值等于( ) A.23 B.-23 C.22 D.-22思路解析：可直接代入求值. x+x 1=3-2+231-=3-2+)23)(23(23+-+=3-2+3+2=23. 答案：A3.已知a-b=23-1,ab=3,则(a+1)(b-1)的值为( ) A.-3 B.33 C.22 D.-22思路解析：依据乘法公式拆开,然后代入即可,(a+1)(b-1)=ab-a+b-1=ab-(a-b)-1 =3-(23-1)-1=3-23+1-1=-3.答案：A4.计算：(26-72)(2+6).思路分析：利用整式及二次根式的运算法则进行计算.解：(26-72)(2+6)=26·2+26·6-72·2-72·6 =43+12-14-143=-103-2.5.如果一个长方形的长是27 m,宽是12 m ，求长方形的周长.(3≈1.732,结果精确到0.1) 思路分析：长方形的周长=2(长+宽).解：长方形的周长=2(27+12)=2(33+23)=103≈10×1.732≈17.3 m.6.已知a=2-2,b=2+2,求222232b ab a b a b a +++÷222b a ab a --的值. 思路分析：先根据分式运算法则进行化简再代入求值. 解：222232b ab a b a b a +++÷222b a ab a --=22)()(b a b a b a ++×)())((b a a b a b a --+=ab. 当a =2-2,b=2+2时，原式=(2-2)(2+2)=22-(2)2=4-2=2.7.已知等腰三角形的腰长为a,底边为b ，底边上的高为h,若a=6+3,b=6+43,求高h. 思路分析：由等腰三角形性质和勾股定理求出高h.解：h=)31221()31239()323()36()2(2222+-+=+-+=-b a =18=32.。

九年级数学二次根式练习题1、函数中，自变量x的取值范围是2、若二次根式有意义，则x的取值范围是．3、在函数y=，自变量x的取值范围是__________。

4、函数的自变量x的取值范围是 .5、若(a－2)2 + =0，则(a+b)2010= ____________.6、若与互为相反数，则x = ，y = ．7、若最简二次根式与是同类二次根式，则x= .8、下列各式计算正确的是A. B.C. D.9、已知，则的值为（）A． B． C． D．10、下列式子运算正确的是（）A． B． C． D．11、是整数,则正整数n的最小值是（）A.4B.5C. 7D. 612、在中，最简二次根式的个数是( )(A)1 (B)2 (C)3 (D)413、使根式有意义的字母x 的取值范围是( )(A)x ＞－1 (B)x ＜－1 (C)x ≥－1且x ≠0 (D)x ≥－1 14、下列二次根式中，不能作为最后结果的是（ ）． A ．B ．C ．D ．15、下列运算中，正确的是……………………………………………………（ ） （A ）； （B ）；（C ）； （D ）．16、17、利用幂的运算性质计算：．参考答案1、 2、x ≥1 3、x ≥5 4、 5、1 6、x = 8，y = 27、1；8、C 9、A 10、D 11、A 12、C 13、C 14、C ． 15、D ；16、17、解：原式=二次根式的加减一. 选择题： 1. 化简a a a 13---得（ ）A. (a －1)a -B. (1－a)a -C. －(a+1)aD. (a －1)a2. 计算的结果是2736123+-（ ） A. 33B. 3C. －36D. －333. 设x ＝35,354-=+y ，则x 与y 的大小关系为（ ） A. x>y B. x ＝y C. x<y D. x ＝－y二. 填空：4. 下列二次根式：①222②12-③81④98⑤118其中为非最简二次根式的有（在横线上写题号） ，与2是同类二次根式的有（写题号）5. 合并同类二次根式的结果为2927xy xy xy -- 。

21．3 二次根式的加减一、双基整合,步步为营1．计算：））=__________，（2=_________．2．若，则x2+2x+1=________．3．已知a2b-ab2=_________．（2+0=________．45．已知菱形两对角线的长分别是（cm，（cm，则它的面积是_________．6．计算：-2的结果是（）A．-7 B．C．-7-8D．-6-87．下列各式正确的是（）A．B．C．=3-2=1 D．2=5-3=28．下列计算正确的是（）=BA．2C D9．已知x-y=5，则（x+1）（y-1）的值是（）A．B．C．D．无法确定10．若三角形的面积为12cm2）cm，则这条边上的高是（）A．B．C．D．11．计算：（1）2×（（2）2+ 2（3）（（（412．解方程组+==二、拓广探索，开发潜能13．已知，5x2+xy+5y2=________．14．若a+1aa-1a=_________．15．设a，小数部分为b，则a-1b的值为（）A．1-2BC．1+2D．16）A．甲的解法正确，乙的解法不正确；B．甲的解法不正确，乙的解法正确C．甲、乙的解法都正确；D．甲、乙的解法都不正确17．设b是任意一个实数x1，x2①求x12+x22；②求x22+bx2-1。

18．已知，三、智能升级链接中考19．化简求值:（）÷，其中a=9，b=4．20．如图，在矩形纸片ABCD中，BC=6，沿EF折叠后，点C落在AB边上的点P处，•点D落在点Q处，AD与PQ相交于点H，∠BPE=30°．（1）求BE、QF的长．（2）求四边形PEFH的面积．参考答案:1．1，2．2 3．4．5．13 26．D 7．C 8．D 9．B 10．C11．（1）1，（2）10，（3）-6，（4）12．x=0， 13．71 14．±1 15．A 16．C17．①b 2+2，②0 18．ab=1，19 120．（1）解：设BE=x ，在Rt △PBE 中，∠BPE=30°，∴PE=2x ，，由题意得EC=EP=2x ，∵BE+EC=BC ，∴3x=6，x=2，即BE=2，∴EC=4，在Rt △APH •中∠APH=60°，∴AH=3，∴在Rt △HQF 中，∠QHF=30°，QF=1．（2）∵S 梯形FECD =12（1+4）×152152S △HFQ =12×∴S 四边形PEFH =S 梯形PEFQ -S △HFQ =S 梯形FECD =S △HFQ。

初中数学二次根式的加减计算专题训练含答案姓名：__________ 班级：__________考号：__________一、计算题（共23题）1、计算：；2、3、计算：()－1＋(－1)2－.4、（1）计算:M5、计算：+∣-5∣．6、计算：7、计算：8、计算：9、|| + || +10、11、（6分）12、计算：；13、计算：（﹣1）3++（﹣1）0﹣．14、计算：．15、计算：16、计算；17、计算．18、计算：（4分）19、计算：20、计算：；21、计算：．22、计算23、计算============参考答案============一、计算题1、【答案】解：原式=。

【考点】实数的运算，二次根式化简，绝对值，负整数指数幂。

【分析】针对二次根式化简，绝对值，负整数指数幂3个考点分别进行计算，然后根据实数的运算法则求得计算结果。

2、3、原式＝＋()2＋12－2×－6＝2＋4－2－6＝－2.4、= 1 +-1+4=-25、解：原式=2-1+5=6．6、 17、8、.9、10、解：原式==11、解：原式＝＝新12、计算：（1）解原式＝1－－＝.13、解：原式=﹣1+2+1﹣=14、15、16、原式=2﹣3=﹣117、原式=﹣3+3=018、 -119、解：原式=（）2—（）2= 2—3= —120、解：原式=4+1-=5-21、解：原式===．22、＝2-4+4×＝ 2-4+2 = 023、 2+。

21.3二次根式的加减同步测试题一、选择题（本题共10小题，每题3分，共30分）1．与 ）A B C D ．2．下列运算正确的是（ ） A.x x x 65=+ B .12223=-C .5252=+D .x b x b x )5(5-=-3．若b a y b a x +=-=,，则xy 的值为 ( )A ．a 2B ．b 2C ．b a +D ．b a -4.x ，小数部分为y y -的值是（ ）A. 35．在△A C ．2个 D ．1个 5. 的值等于20072008)23()23(+-（ ） A. 2 B. －2 C. 23- D. 32-6．对于所有实数,a b ，下列等式总能成立的是（ ）A. 2a b =+a b =+22a b =+a b =+7．下列计算正确的是（ ）4=± Ｂ．1=4= 623=8．下列式子中正确的是（ ）= B. a b =-C. (a b =-2== 9．若 a + b 与 a － b 互为倒数，则（ ）A 、a=b －1B 、a=b+1C 、a+b=1D 、a+b=－110．下列计算错误．．的是( )=(D)3二、填空题（本题共8小题，每题4分，共32分）11．若最简二次根式____,____a b ==12是同类二次根式的是 。

13． 5的整数部分是_________14=15．方程2（x －1）＝x ＋1的解是____________．16．已知251-=x ，则x x 1-的值等于 。

17．如图，矩形内两相邻正方形的面积分别是2和6，那么矩形内阴影部分的面积是 ．（结果可用根号表示）18．图7是由边长为1m 的正方形地砖铺设的地面示意图，小明沿图中所示的折线从A →B →C 所走的路程为_______m ．（结果保留根号）三、解答题（本题共8小题，共58分）19．（1）123478143527a a a a a a +-- （2）()()()413903b a b a a b a b a ab b +-+> 20．一个直角三角形的两条直角边长分别是,cm )23(,cm )23(+-求这个三角形的面积和周长21．（1）38545226⨯--()（2）()()32533253+- （3）()-+1322 22．已知最简根式y9y x 3y 62x 5-+--和是同类根式，求x ，y 的值23．化简（235+-）（235--）24．已知菱形ABCD 的对角线AC ＝472,472-=+BD ，求菱形的边长和面积。

2022-2023学年华东师大版九年级数学上册《21.3二次根式的加减》同步练习题（附答案）一．选择题1．在、、中与能合并的二次根式的个数是（）A．0B．1C．2D．32．下列运算正确的是（）A．﹣＝B．＝2C．﹣＝D．＝2﹣3．计算×﹣的结果是（）A．7B．6C．7D．24．若的整数部分为x，小数部分为y，则（2x+）y的值是（）A．B．3C．D．﹣35．如图，从一个大正方形中裁去面积为30cm2和48cm2的两个小正方形，则余下部分的面积为（）A．78 cm2B．cm2C．cm2D．cm2二．填空题6．计算：（）0＝．7．已知x、y满足方程组，则3x﹣y的值为．8．如果最简二次根式与能合并，那么a＝．9．计算＝．10．（+）2021×（﹣）2022＝．11．当x＝1+时，代数式x2﹣2x+2021＝．12．已知三角形底边的边长是cm，面积是cm2，则此边的高线长cm．三．解答题13．计算：．14．化简15．计算：（3﹣）÷+（1﹣）．16．已知a＝+1，b＝﹣1，计算：（1）2a+2b（2）a2+b217．已知，（1）求a+b，a﹣b的值（2）求代数式的值．18．化简：（4﹣6）÷﹣（+）（﹣）19．细心观察图形，认真分析各式，然后解答问题：OA1＝1；OA2＝＝；S1＝×1×1＝；OA3＝＝；S2＝××1＝；OA4＝＝；S3＝××1＝；（1）推算出OA10＝．（2）若一个三角形的面积是．则它是第个三角形．（3）用含n（n是正整数）的等式表示上述面积变化规律；（4）求出S12+S22+S23+…+S2100的值．20．设一个三角形的三边长分别为a，b，c，p＝（a+b+c），则有下列面积公式：S＝（海伦公式），S＝（秦九韶公式）．请选择合适的公式求下列三角形的面积：（1）三角形的三边长依次为a＝5，b＝6，c＝7．（2）三角形的三边长依次为a＝，b＝，c＝．参考答案一．选择题1．解：＝3、＝、＝，∴与能合并有和，共2个．故选：C．2．解：A、与不是同类项，不能合并，故本选项错误；B、＝，故本选项错误；C、﹣＝2﹣＝，故本选项正确；D、＝﹣2，故本选项错误．故选：C．3．解：原式＝×﹣＝××﹣＝7﹣＝6．故选：B．4．解：∵3＜＜4，∴的整数部分x＝2，则小数部分是：6﹣﹣2＝4﹣，则（2x+）y＝（4+）（4﹣）＝16﹣13＝3．故选：B．5．解：从一个大正方形中裁去面积为30cm2和48cm2的两个小正方形，大正方形的边长是+＝（+4）cm，留下部分（即阴影部分）的面积是（+4）2﹣30﹣48＝8＝24（cm2）．故选：D．二．填空题6．解：原式＝3﹣﹣+1＝+1．7．解：，①+②得：3x﹣y＝4，故答案为：4．8．解：根据题意得，1+a＝4a﹣2，移项合并，得3a＝3，系数化为1，得a＝1．故答案为：1．9．解：原式＝＝3．10．解：原式＝[（+）×（﹣）]2021×（﹣）＝（﹣1）2021×（﹣）＝﹣1×（﹣）＝﹣，故答案为：﹣．11．解：∵x＝1+时，∴x﹣1＝，∴（x﹣1）2＝3，∴x2﹣2x+1＝3，∴x2﹣2x＝2，∴原式＝2+2021＝2023，故答案为：2023．12．解：设三角形此边上的高为x厘米，由题意，得×x＝，解得x＝2．故答案为：2．三．解答题13．解：原式＝﹣3+2+2＝3﹣．14．解：原式＝4+﹣12﹣＝﹣8．15．解：原式＝3﹣+﹣6＝﹣3．16．解：（1）当a＝+1，b＝﹣1时，原式＝2（a+b）＝2×（+1+﹣1）＝2×2＝4；（2）当a＝+1，b＝﹣1时，原式＝（+1）2+（﹣1）2＝3+2+3﹣2＝6．17．解：（1）∵a＝2+，b＝2﹣，∴a+b＝（2+）+（2﹣）＝4，a﹣b＝（2+）﹣（2﹣）＝2；（2）（1﹣）÷（）＝.，＝a﹣b，由（1）的结论得：原式＝2．18．解：原式＝（4﹣2）÷﹣（5﹣3）＝2÷﹣2＝2﹣2＝0．19．解：（1））∵OA n2＝n，∴OA10＝．故答案为：；（2）若一个三角形的面积是，∵S n＝＝，∴＝2＝，∴它是第20个三角形．故答案为：20；（3）结合已知数据，可得：OA n2＝n；S n＝；（4）S12+S22+S23+…+S2100＝++++…+＝＝20．解：（1）∵，由海伦公式得：＝＝＝；（2）设，，，代入秦九韶公式，得：＝＝＝＝；。

第二十一章 二次根式测试1 二次根式学习要求掌握二次根式的概念和意义，会根据算术平方根的意义进行二次根式的运算．课堂学习检验一、填空题1．a +1表示二次根式的条件是______． 2．当x ______时，12--x 有意义，当x ______时，31+x 有意义． 3．若无意义2+x ，则x 的取值范围是______． 4．直接写出下列各式的结果： (1)49＝_______；(2)2)7(_______； (3)2)7(-_______；(4)2)7(--_______； (5)2)7.0(_______；(6)22])7([- _______． 二、选择题5．下列计算正确的有( )．①2)2(2=- ②22=- ③2)2(2=- ④2)2(2-=- A ．①、② B ．③、④C ．①、③D ．②、④6．下列各式中一定是二次根式的是( )． A ．23-B ．2)3.0(-C ．2-D ．x7．当x =2时，下列各式中，没有意义的是( )． A ．2-xB ．x -2C ．22-xD ．22x -8．已知,21)12(2a a -=-那么a 的取值范围是( )．A ．21>aB ．21<a C ．21≥a D ．21≤a 三、解答题9．当x 为何值时，下列式子有意义? (1);1x -(2);2x -(3);12+x (4)⋅+-xx2110．计算下列各式：(1);)23(2 (2);)1(22+a(3);)43(22-⨯-(4).)323(2-综合、运用、诊断一、填空题11．x 2-表示二次根式的条件是______． 12．使12-x x有意义的x 的取值范围是______． 13．已知411+=-+-y x x ，则x y 的平方根为______． 14．当x =－2时，2244121x x x x ++-+-＝________． 二、选择题15．下列各式中，x 的取值范围是x ＞2的是( )．A ．2-xB ．21-xC ．x -21D ．121-x16．若022|5|=++-y x ，则x －y 的值是( )． A ．－7B ．－5C ．3D ．7三、解答题17．计算下列各式：(1);)π14.3(2-(2);)3(22--(3);])32[(21-(4).)5.03(2218．当a =2，b =－1，c =－1时，求代数式acb b 42-±-的值．拓广、探究、思考19．已知数a ，b ，c 在数轴上的位置如图所示：化简：||)(||22b b c c a a ---++-的结果是：______________________．20．已知△ABC 的三边长a ，b ，c 均为整数，且a 和b 满足.09622=+-+-b b a 试求△ABC 的c 边的长．测试2 二次根式的乘除(一)学习要求会进行二次根式的乘法运算，能对二次根式进行化简．课堂学习检测一、填空题1．如果y x xy ⋅=24成立，x ，y 必须满足条件______．2．计算：(1)=⨯12172_________；(2)=--)84)(213(__________； (3)=⨯-03.027.02___________．3．化简：(1)=⨯3649______；(2)=⨯25.081.0 ______；(3)=-45______． 二、选择题4．下列计算正确的是( )． A ．532=⋅ B ．632=⋅C ．48=D ．3)3(2-=-5．如果)3(3-=-⋅x x x x ，那么( )．A ．x ≥0B ．x ≥3C ．0≤x ≤3D ．x 为任意实数6．当x =－3时，2x 的值是( )． A ．±3 B ．3 C ．－3 D ．9三、解答题7．计算：(1);26⨯(2));33(35-⨯- (3);8223⨯(4);1252735⨯ (5);131aab ⋅(6);5252ac c b b a ⋅⋅(7);49)7(2⨯- (8);51322-(9).7272y x8．已知三角形一边长为cm 2，这条边上的高为cm 12，求该三角形的面积．综合、运用、诊断一、填空题9．定义运算“@”的运算法则为：,4@+=xy y x 则(2@6)@6=______．10．已知矩形的长为cm 52，宽为cm 10，则面积为______cm 2．11．比较大小：(1)23_____32；(2)25______34；(3)－22_______－6． 二、选择题12．若b a b a -=2成立，则a ，b 满足的条件是( )．A ．a ＜0且b ＞0B ．a ≤0且b ≥0C ．a ＜0且b ≥0D ．a ，b 异号13．把4324根号外的因式移进根号内，结果等于( )． A ．11- B ．11C ．44-D ．112三、解答题14．计算：(1)=⋅x xy 6335_______；(2)=+222927b a a _______；(3)=⋅⋅21132212_______； (4)=+⋅)123(3_______．15．若(x －y ＋2)2与2-+y x 互为相反数，求(x ＋y )x 的值．拓广、探究、思考16．化简：(1)=-+1110)12()12(________；(2)=-⋅+)13()13(_________．测试3 二次根式的乘除(二)学习要求会进行二次根式的除法运算，能把二次根式化成最简二次根式．课堂学习检测一、填空题1．把下列各式化成最简二次根式：(1)=12______；(2)=x 18______；(3)=3548y x ______；(4)=xy______；(5)=32______；(6)=214______；(7)=+243x x ______；(8)=+3121______． 2．在横线上填出一个最简单的因式，使得它与所给二次根式相乘的结果为有理式，如：23 与.2(1)32与______； (2)32与______；(3)a 3与______； (4)23a 与______； (5)33a 与______． 二、选择题 3．xx x x -=-11成立的条件是( )． A ．x ＜1且x ≠0 B ．x ＞0且x ≠1C ．0＜x ≤1D ．0＜x ＜14．下列计算不正确的是( )． A ．471613= B ．xy x x y 63132= C ．201)51()41(22=-D ．x x x3294= 5．把321化成最简二次根式为( )． A ．3232 B ．32321C ．281 D ．241 三、计算题 6．(1);2516 (2);972(3);324 (4);1252755÷-(5);1525 (6);3366÷(7);211311÷(8).125.02121÷综合、运用、诊断一、填空题7．化简二次根式：(1)=⨯62________(2)=81_________(3)=-314_________ 8．计算下列各式，使得结果的分母中不含有二次根式： (1)=51_______(2)=x 2_________(3)=322__________(4)=y x5__________ 9．已知,732.13≈则≈31______；≈27_________．(结果精确到0．001) 二、选择题10．已知13+=a ，132-=b ，则a 与b 的关系为( )． A ．a =b B ．ab =1C ．a =－bD ．ab =－111．下列各式中，最简二次根式是( )．A ．yx -1 B ．ba C ．42+x D ．b a 25三、解答题12．计算：(1);3b a ab ab ⨯÷(2);3212y xy ÷(3)⋅++ba b a13．当24,24+=-=y x 时，求222y xy x +-和xy 2＋x 2y 的值．拓广、探究、思考14．观察规律：,32321,23231,12121-=+-=+-=+……并求值．(1)=+2271_______；(2)=+10111_______；(3)=++11n n _______．15．试探究22)(a 、a 与a 之间的关系．测试4 二次根式的加减(一)学习要求掌握可以合并的二次根式的特征，会进行二次根式的加、减运算．课堂学习检测一、填空题1．下列二次根式15,12,18,82,454,125,27,32化简后，与2的被开方数相同的有______，与3的被开方数相同的有______，与5的被开方数相同的有______．2．计算：(1)=+31312________； (2)=-x x 43__________．二、选择题3．化简后，与2的被开方数相同的二次根式是( )． A ．10B ．12C ．21 D ．61 4．下列说法正确的是( )．A ．被开方数相同的二次根式可以合并B ．8与80可以合并C ．只有根指数为2的根式才能合并D ．2与50不能合并5．下列计算，正确的是( )． A ．3232=+B ．5225=-C ．a a a 26225=+D ．xy x y 32=+ 三、计算题6．.48512739-+7．.61224-+8．⋅++3218121 9．⋅---)5.04313()81412(10．.1878523x x x +- 11．⋅-+xx x x 1246932综合、运用、诊断一、填空题12．已知二次根式b a b +4与b a +3是同类二次根式，(a ＋b )a 的值是______．13．3832ab 与ba b 26无法合并，这种说法是______的．(填“正确”或“错误”) 二、选择题14．在下列二次根式中，与a 是同类二次根式的是( )．A ．a 2B ．23aC ．3aD ．4a三、计算题 15．.)15(2822180-+-- 16．).272(43)32(21--+ 17．⋅+-+bb a b a a124118．.21233ab bb a aba bab a-+-四、解答题19．化简求值：y y xy xx 3241+-+，其中4=x ，91=y ．20．当321-=x 时，求代数式x 2－4x ＋2的值．拓广、探究、思考21．探究下面的问题：(1)判断下列各式是否成立?你认为成立的，在括号内画“√”，否则画“×”．①322322=+（ ） ②833833=+（ ） ③15441544=+（ ） ④24552455=+（ ）(2)你判断完以上各题后，发现了什么规律?请用含有n 的式子将规律表示出来，并写出n 的取值范围．(3)请你用所学的数学知识说明你在(2)题中所写式子的正确性．测试5 二次根式的加减(二)学习要求会进行二次根式的混合运算，能够运用乘法公式简化运算．课堂学习检测一、填空题1．当a =______时，最简二次根式12-a 与73--a 可以合并． 2．若27+=a ，27-=b ，那么a ＋b =______，ab =______． 3．合并二次根式：(1)=-+)18(50________；(2)=+-ax xax45________． 二、选择题4．下列各组二次根式化成最简二次根式后的被开方数完全相同的是( )． A ．ab 与2abB mn 与nm 11+ C ．22n m +与22n m - D ．2398b a 与4329b a5．下列计算正确的是( )． A ．b a b a b a -=-+2))(2( B ．1239)33(2=+=+C ．32)23(6+=+÷D ．641426412)232(2-=+-=-6．)32)(23(+-等于( )． A ．7 B ．223366-+- C ．1D ．22336-+三、计算题(能简算的要简算) 7．⋅-121).2218( 8．).4818)(122(+-9．).32841)(236215(-- 10．).3218)(8321(-+11．.6)1242764810(÷+- 12．.)18212(2-综合、运用、诊断一、填空题13．(1)规定运算：(a *b )=｜a －b ｜，其中a ，b 为实数，则=+7)3*7(_______．(2)设5=a ，且b 是a 的小数部分，则=-baa ________． 二、选择题14．b a -与a b -的关系是( )． A ．互为倒数 B ．互为相反数 C ．相等D ．乘积是有理式15．下列计算正确的是( )．A ．b a b a +=+2)(B ．ab b a =+C ．b a b a +=+22D ．a aa =⋅1三、解答题 16．⋅+⋅-221221 17．⋅--+⨯2818)212(218．.)21()21(20092008-+ 19．.)()(22b a b a --+四、解答题20．已知,23,23-=+=y x 求(1)x 2－xy ＋y 2；(2)x 3y ＋xy 3的值．21．已知25-=x ，求4)25()549(2++-+x x 的值．拓广、探究、思考22．两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，我们说这两个代数式互为有理化因式．如：a 与a ，63+与63-互为有理化因式． 试写下列各式的有理化因式： (1)25与______；(2)y x 2-与______；(3)mn 与______； (4)32+与______； (5)223+与______；(6)3223-与______．23．已知,732.13,414.12≈≈求)23(6-÷．(精确到0.01)答案与提示第二十一章 二次根式测试11．a ≥－1．2．<1， >－3．3．x <－2．4．(1)7； (2)7； (3)7； (4)－7； (5)0.7； (6)49． 5．C ． 6．B ． 7．D ． 8．D ．9．(1)x ≤1；(2)x ＝0；(3)x 是任意实数；(4)x ≤1且x ≠－2．10．(1)18；(2)a 2＋1；(3);23- (4)6．11．x ≤0． 12．x ≥0且⋅=/21x 13．±1． 14．0． 15．B ． 16．D ． 17．(1)π－3．14；(2)－9；(3);23 (4)36． 18．21-或1．19．0． 20．提示：a ＝2，b ＝3，于是1<c <5，所以c ＝2，3，4．测试2 1．x ≥0且y ≥0．2．(1);6 (2)24；(3)－0.18．3．(1)42；(2)0.45；(3).53- 4．B ． 5．B ． 6．B ．7．(1);32 (2)45； (3)24； (4);53 (5);3b(6);52(7)49； (8)12； (9)⋅y xy 263 8．.cm 629．.72 10．210． 11．(1)>；(2)>；(3)<． 12．B ． 13．D ．14．(1);245y x (2);332b a + (3) ;34 (4)9． 15．1． 16．(1);12- (2).2测试31．(1);32 (2);23x (3);342xy y x (4);xxy (5);36 (6);223 (7);32+x x (8)630． 2．.3)5(;3)4(;3)3(;2)2(;3)1(a a 3．C ． 4．C ． 5．C ． 6．.4)8(;322)7(;22)6(;63)5(;215)4(;22)3(;35)2(;54)1(-7．⋅-339)3(;42)2(;32)1( 8．⋅y y x x x 55)4(;66)3(;2)2(;55)1( 9．0.577，5.196． 10．A ． 11．C ． 12．.)3(;33)2(;)1(b a x bab+ 13．.112;2222222=+=+-y x xy y xy x14．.1)3(;1011)2(;722)1(n n -+--15．当a ≥0时，a a a ==22)(；当a <0时，a a -=2，而2)(a 无意义．测试41．.454,125;12,27;18,82,32 2．(1).)2(;33x 3．C ． 4．A ． 5．C ． 6．.33 7．.632+ 8．⋅827 9．.23+ 10．.214x 11．.3x 12．1． 13．错误． 14．C ． 15．.12+ 16．⋅-423411 17．.321b a + 18．0．19．原式,32y x+=代入得2． 20．1． 21．(1)都画“√”；(2)1122-=-+n n nn n n (n ≥2，且n 为整数)；(3)证明：⋅-=-=-+-=-+111)1(1223222n nn n n n n n n n n n 测试51．6． 2．.3,72 3．(1);22 (2) .3ax - 4．D ． 5．D ． 6．B ． 7．⋅668．.1862-- 9．.3314218-10．⋅417 11．.215 12．.62484-13．(1)3；(2).55-- 14．B ． 15．D ．16．⋅-4117．2． 18．.21-19．ab 4(可以按整式乘法，也可以按因式分解法)．20．(1)9； (2)10． 21．4．22．(1)2； (2)y x 2-； (3)mn ； (4)32-； (5)223-； (6)3223+(答案)不唯一． 23．约7.70．第二十一章 二次根式全章测试一、填空题 1．已知mnm 1+-有意义，则在平面直角坐标系中，点P (m ，n )位于第______象限． 2．322-的相反数是______，绝对值是______．3．若3:2:=y x ，则=-xy y x 2)(______．4．已知直角三角形的两条直角边长分别为5和52，那么这个三角形的周长为______． 5．当32-=x 时，代数式3)32()347(2++++x x 的值为______． 二、选择题6．当a <2时，式子2)2(,2,2,2-+--a a a a 中，有意义的有( )． A ．1个 B ．2个C ．3个D ．4个7．下列各式的计算中，正确的是( )． A ．6)9(4)9()4(=-⨯-=-⨯- B ．7434322=+=+C ．9181404122=⨯=-D ．2323= 8．若(x ＋2)2＝2，则x 等于( )． A ．42+B ．42-C ．22-±D ．22±9．a ，b 两数满足b <0<a 且｜b ｜>｜a ｜，则下列各式中，有意义的是( )． A ．b a +B ．a b -C ．b a -D ．ab10．已知A 点坐标为),0,2(A 点B 在直线y ＝－x 上运动，当线段AB 最短时，B 点坐标( )．A ．(0，0)B ．)22,22(- C ．(1，－1) D ．)22,22(-三、计算题11．.1502963546244-+- 12．).32)(23(--13．.25341122÷⋅ 14．).94(323ab ab ab a aba b+-+15．⋅⋅-⋅ba b a ab ba 3)23(35 16．⋅÷+--+xy yx y x xy yx y )(四、解答题17．已知a 是2的算术平方根，求222<-a x 的正整数解．18．已知：如图，直角梯形ABCD 中，AD ∥BC ，∠A ＝90°，△BCD 为等边三角形，且AD 2=，求梯形ABCD 的周长．附加题19．先观察下列等式，再回答问题．①;2111111112111122=+-+=++②;6111212113121122=+-+=++③⋅=+-+=++12111313114131122(1)请根据上面三个等式提供的信息，猜想2251411++的结果；(2)请按照上面各等式反映的规律，试写出用n(n为正整数)表示的等式．20．用6个边长为12cm的正方形拼成一个长方形，有多少种拼法?求出每种长方形的对角线长(精确到0.1cm，可用计算器计算)．答案与提示第二十一章 二次根式全章测试1．三． 2．.223,223-- 3．.2665- 4．.555+ 5．.32+ 6．B ． 7．C ． 8．C ． 9．C ． 10．B ． 11．.68- 12．.562- 13．⋅1023 14．.2ab - 15．.293ab b a - 16．0． 17．x <3；正整数解为1，2． 18．周长为.625+ 19．(1);2011141411=+-+(2).)1(111111)1(11122++=+-+=+++n n n nn n20．两种：(1)拼成6×1，对角线);cm (0.733712721222≈=+(2)拼成2×3，对角线3.431312362422≈=+(cm)．。

九年级数学二次根式的加减同步练习一. 选择题：1. （市海淀区）在下列二次根式中与2是同类二次根式的是（） A. 8 B. 10 C. 12 D. 272. 化简372-的结果是（） A.72-B. 72+C. 372()-D. 372()+3. 下列各组二次根式中，是同类二次根式的一组是（） A. 32ab 和32ab c B. 27498b a a b和C.3234a b 和2343a bD.b a 2和2a b4. 已知x=-32，那么x x+1的值等于（） A. 23 B. -23 C. 22 D. -225. 若y y x y 24410++++-=，则xy 的值等于（） A. -6 B. -2 C. 2 D. 66. （2001年某某市中考题）如果表示a b ,两个实数的点在数轴上的位置如下图所示，那么化简||a b a a b b-+++222的结果等于（）． A. 2aB. 2bC. -2aD. -2bb a 0二. 填空题1. （2002年某某省某某市中考题）能使等式a a aa +=+33成立的a 的取值X 围是_______．2. 若||a b a b -+++124与互为相反数，则()a b +=2004__________． 3. 最简二次根式831221x x 与+是同类二次根式，则x 的值为______．4. 化简M x x x x =++--+12144922的结果是________．三. 化简：1. （2001年某某市中考题）132132-++；2. （2002年某某市中考题）已知||a a =-，化简||()1222-+-+a a a3. 设18≤≤x ，化简：x x 21025-+四. 求代数式的值：1. （某某市）化简并求值：()()()m n m n m n +++-23；其中m n ==21，． 2. （某某市课改实验区）先化简，再求值：()x x x x +--÷--115141，其中x =-524． 3. （某某省课改实验区）课堂上，李老师给大家出了这样一道题：当2253x -，分别等于，73+时，求代数式x x x x x 22211221-+-÷-+的值．小明一看，“太复杂了，怎么算呢？”你能帮小明解决这个问题吗？请你写出具体过程．4. （某某回族自治区课改实验区）已知a =2，求代数式()111112a a a a--+⋅-的值． 5. （某某市课改实验区）先化简，再求值：()211112x x x x x --+÷-，其中x =-21．五. 比较大小1. 比较175186--与的大小；2. 比较15141413--与的大小； 3. 比较6776与的大小；4. 比较310522++与的大小．【试题答案】一. 选择题：1. A2. B3. D4. A5. A6. D分析：根据数轴上的点与原点的位置关系，判断该数的正、负；根据两数的对应点的相互位置关系，判断这两个数的大小关系． 解：由图可知b a <<0， ∴->+<a b a b 00，∴原式=-++=-++||()||||ab ab ab ab 2b 2)b a (b a -=+--= 故选D ．二.1. 解：等式a a aa +=+33成立的条件是 a a≥+>⎧⎨⎩030，，即a a ≥>-⎧⎨⎩3，即a ≥0故答案为a ≥0． 2. 解析： ||a b a b -+++124与互为相反数．∴-++++=||a b a b 1240 而||ab a b -+≥++≥10240，， ∴-+=++=⎧⎨⎩a b a b 10240，∴=-=-⎧⎨⎩a b 21 ∴+=--=-=()()()a b 200420042004200421333. 答案为1.4. 分析：容易看出M x x =+--||||17，而且x R ∈，所以应按上题“点评”中（2）的方法，用两个零点-1和7，把数轴分成三类进行讨论． 解：M x x =+--()()1722=+--||||x x 17-17（1）当x <-1时，x x +<-<1070，， M x x =-+--=-()()178； （2）-≤<17x 时，x x +≥-<1070，， M x x x =+--=-()()1726； （3）当x ≥7时，x x +>-≥1070，， M x x =+--=()()178 ∴=-<---≤<≥⎧⎨⎪⎩⎪M x x x x 81261787,(),,(),()三.1. 解：原式=+-++--+323232323232()()()()=+-+--=++-=323232323232232222()()()()2. （2002年某某市中考题）已知||a a =-，化简：a 2)2a (|a -1|2+-+ 分析：先由||a a =-确定a 的符号．解： -=≥a a ||0， ∴≤a 0∴原式a 2|2a ||a 1|+-+-= =-+-+()()122a a a=33. 设18≤≤x ，化简：x x 21025-+ 解： x x x 2210255-+=-()，且18≤≤x ∴由下图可知1 5 8当58≤≤x 时，有x -≥50； 当15≤<x 时，有x -<50因此，x x x 2210255-+=-()⎩⎨⎧≤≤-≤≤-=)5x 1(x 5)8x 5(5x四. 1. 原式=++++--=-m m n n m m n m n n m n22222223322 当m n ==21，时，原式=-=-=2224222() 2. 原式=---⋅--=+x x x x x 21151144当x =-524时，原式=-+=5244523. 原式=-+-⋅+-=()()()()x x x x x 111121122当37,225,3x +-分别为时，原式=124. 原式=+--+-⋅+-=a a a a a a a a1111112()()()()()当a =2时，原式==222 5. 原式=21111111x x x x x x x x ()()()()()()+--+-⋅+-=+x x 23当x =-21时，原式=-+-=()()2132122五. 1. 比较175186--与的大小．分析：分子相同，正常思路，可比较分母的大小，但分母大小不易看出． 方法：分母有理化法．解：175752-=+186862-=+，分母均为2，将分子比大小即可． 7528620+-+< ∴-<-1751862. 比较15141413--与的大小． 分析：可将分母看成1，进行分子有理化． 方法：分子有理化法．解：151411514-=+141311413-=+，显然分子相同，比较分母大小即可．15141413+>+，分子相同时分母大的值反而小．∴-<-151414133. 比较67与76的大小． 方法：比较被开方数法．解： 67736252=⨯=∴=⨯=76649294∴<252294即6776< 4. 比较310+与522+的大小． 方法：比较两数的平方法． 注：这两数须都大于0．解： ()310310230132302+=++=+ ()52258410132402+=++=+ 显然230240< ∴+<+1323013240即310522+<+。