河南省罗山县楠杆高级中学2021届高三上学期第五次周考数学(文)试题 Word版含答案
- 格式:docx
- 大小:284.83 KB
- 文档页数:12

2020年10月15日2020-2021学年普通高中高三第一次教学质量检测数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分㊂考生作答时,将答案答在答题卡上,在本试卷上答题无效㊂考试结束后,将本试卷和答题卡一并交回㊂注意事项:1.答题前,考生务必将本人的姓名㊁准考证号等考生信息填写在答题卡上,并用2B铅笔将准考证号填涂在相应位置㊂2.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色墨水签字笔书写,字体工整㊁笔迹清楚㊂3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效㊂4.保持卡面清洁,不折叠,不破损㊂第Ⅰ卷一㊁选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={x||x-2|ɤ1},B={x|y=22-x},则AɘB等于A.[-1,2]B.(2,3]C.[1,2)D.[1,3)2.若函数f(x)=(m2-2m-2)x m-1是幂函数,则m等于A.-1B.3或-1C.1ʃ3D.33.已知[x]表示不超过实数x的最大整数,g(x)=[x]为取整函数,x0是函数f(x)=l n x+x-4的零点,则g(x0)等于A.4B.5C.2D.34.近年来,随着 一带一路 倡议的推进,中国与沿线国家旅游合作越来越密切,中国到 一带一路 沿线国家的游客人数也越来越多,如图是2013-2018年中国到 一带一路 沿线国家的游客人次情况,则下列说法正确的是①2013-2018年中国到 一带一路 沿线国家的游客人次逐年增加②2013-2018年这6年中,2014年中国到 一带一路 沿线国家的游客人次增幅最小③2016-2018年这3年中,中国到 一带一路 沿线国家的游客人次每年的增幅基本持平5.已知命题p :对任意x ɪR ,总有2x >x 2;q :a b >4 是 a >2,b >2 的充分不必要条件,则下列命题为真命题的是A .p ɡq B .┐p ɡq C .p ɡ┐q D.┐p ɡ┐q6.在ΔA B C 中,øA B C =π4,A B =2,B C =3,则s i n øB A C 等于A.1010B .105C .31010 D.557.我国著名数学家华罗庚先生曾说图像数缺形时少直观,形缺数时难人微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数图像来研究函数的性质,也常用函数的解析式来研究函数图像的特征,已知函数f (x )的图像如图所示,则函数f (x )的解析式可能是A.f (x )=(4x +4-x )|x |B .f (x )=(4x -4-x )l o g 2|x |C .f (x )=(4x +4-x )l o g 12|x |D.f (x )=(42+4-x )l o g 2|x |8.已知定义在R 上的函数f (x )满足f (2-x )+f (x )=0,当x >1时,f (x )=x -2,则不等式f (x )<0的解集为A.(1,2)B .(-ɕ,0)C .(-ɕ,0)ɣ(1,2) D.(0,2)9.已知x =π4是函数f (x )=s i n (ωx +φ)(0<ω<3,0<ω<π)的一个零点,将f (x )的图象向右平移π12个单位长度,所得图象关于y 轴对称,则函数f (x )的单调递增区间是A.[-3π4+2k π,π12+2k π],k ɪZ B .[-5π12+4k π3,π4+4k π3],k ɪZ C .[-5π12+2k π,π4+2k π],k ɪZ D.[-3π4+4k π3,-π12+4k π3],k ɪZ 10.已知定义在R 上的奇函数f (x )和偶函数g (x )满足f (x )+g (x )=a x -a -x +2(a >0且a ʂ1),若g (2)=a ,则函数f (x 2+2x )的单调递增区间为A.(-1,1)B .(-1,+ɕ)C .(1,+ɕ) D.(-ɕ,1)11.已知函数f (x )=c o s x s i n 2x ,给出下列命题:①∀x ɪR ,都有f (-x )=-f (x )成立;②存在常数T ʂ0,∀x ɪR 恒有f (x +T )=f (x )成立;③f (x )的最大值为239;④y =f (x )在[-π6,π6]上是增函数㊂以上命题中正确的为A.①②③④B .②③C .①②③ D.①②④12.已知定义在(-ɕ,0)ɣ(0,+ɕ)上的函数f (x ),且f (1)=1,函数f (x +1)的图象关于点(-1,0)中心对称,对于任意x 1,x 2ɪ(0,+ɕ),x 1ʂx 2,都有x 20191f (x 1)-x 20192f (x 2)x 1-x 2>0成立.则f (x )ɤ1x 2019的解集为A.[-1,1]B .(-ɕ,-1]ɣ[1,+ɕ)第Ⅱ卷二㊁填空题:本大题共4个小题,每小题5分,共20分,把答案填在答题卡的相应位置.13.ʏπ20(c o s x+s i n x)d x的值为.14.已知c o s(α+β)=513,s i nβ=35,α,β均为锐角,则s i nα的值是.15.若b>a>1且3l o g a b+6l o g b a=11,则a3+2b-1的最小值为.16.已知函数f(x)=x2-1,x<1l n xx,xȡ1ìîíïïïï,若关于x的方程2[f(x)]2+(1-2m)f(x)-m=0有5个不同的实数解,则实数m的取值范围是.三㊁解答题:本大题共6小题,共70分,解答应写出文字说明㊁证明过程或演算步骤.17.(本小题满分10分)已知命题p:关于x的不等式x2-4x+2m<0无解;命题q:指数函数f(x)=(2m-1)x是R上的增函数.(Ⅰ)若命题pɡq为真命题,求实数m的取值范围;(Ⅱ)若满足p为假命题且q为真命题的实数m的取值范围是集合A,集合B={x|2t-1<x< 13-t2},且A⊆B,求实数t的取值范围.18.(本小题满分12分)已知函数f(x)=x3+a x2+b x+c在x=-1与x=2处都取得极值.(Ⅰ)求a,b的值及函数f(x)的单调区间;(Ⅱ)若对xɪ[-1,3],不等式f(x)+32c<c2恒成立,求c的取值范围.19.(本小题满分12分)近几年美国对中国芯片的技术封锁,激发了中国 芯 的研究热潮.某公司研发的A,B两种芯片都已经获得成功.该公司研发芯片已经耗费资金2千万元,现在准备投入资金进行生产.经市场调查与预测,生产A芯片的毛收入与投入的资金成正比,已知每投入1千万元,公司获得毛收入0.25千万元;生产B芯片的毛收入y(千万元)与投入的资金x(千万元)的函数关系为y= k xα(x>0),其图像如图所示.(Ⅰ)试分别求出生产A,B两种芯片的毛收入y(千万元)与投入资金x(千万元)的函数关系式;(Ⅱ)现在公司准备投入4亿元资金同时生产A,B两种芯片,求可以获得的最大利润是多少㊂20.(本小题满分12分)在①a=2,②B=π4,③c=3b这三个条件中任选两个,补充在下面的问题中,并解决该问题.在ΔA B C中,a,b,c分别为内角A,B,C的对边,且满足(b-a)(s i n B+s i n A)= c(3s i n B-s i n C).(Ⅰ)求A的大小;(Ⅱ)已知,,若ΔA B C存在,求ΔA B C的面积;若ΔA B C不存在,说明理由.21.(本小题满分12分)已知函数f(x)=4x-m㊃2x+1(mɪR),g(x)=2x-12x+1.(Ⅰ)求函数f(x)在区间[1,+ɕ)上的最小值;(Ⅱ)若存在不相等的实数a,b同时满足f(a)+f(b)=0,g(a)+g(b)=0,求m的取值范围.22.(本小题满分12分)设函数f(x)=x l n x-a x2(Ⅰ)若函数f(x)有两个极值点,求实数a的取值范围;(Ⅱ)设g(x)=a x(x-2)-f(x)x,若当a<0时,函数g(x)的两个极值点x1,x2满足x1<x2,求证:g(x2)>94.。

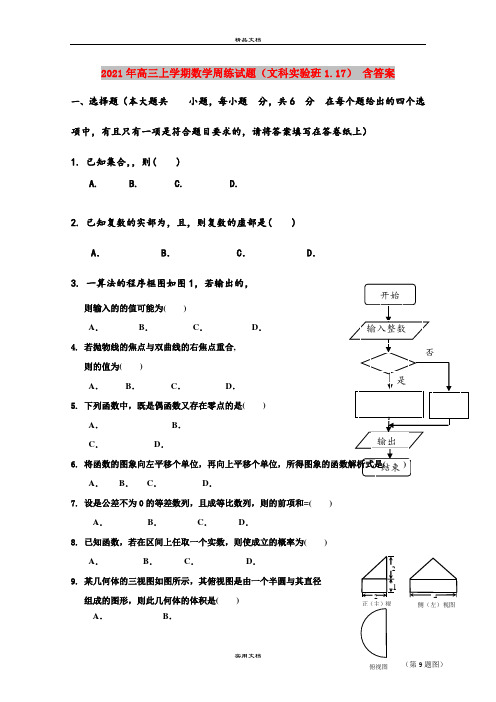
开始输入整数是否输出结束侧(左)视图4212正(主)视2021年高三上学期数学周练试题(文科实验班1.17) 含答案一、选择题(本大题共小题,每小题分,共6分在每个题给出的四个选项中,有且只有一项是符合题目要求的,请将答案填写在答卷纸上) 1. 已知集合,,则( )A. B. C. D.2. 已知复数的实部为,且,则复数的虚部是( ) A . B . C . D .3. 一算法的程序框图如图1,若输出的,则输入的的值可能为( )A .B .C .D . 4. 若抛物线的焦点与双曲线的右焦点重合, 则的值为( )A .B .C .D . 5. 下列函数中,既是偶函数又存在零点的是( ) A . B . C . D .6. 将函数的图象向左平移个单位,再向上平移个单位,所得图象的函数解析式是( )A .B .C .D .7. 设是公差不为0的等差数列,且成等比数列,则的前项和=( ) A . B . C .D .8. 已知函数,若在区间上任取一个实数,则使成立的概率为( ) A . B . C .D .9. 某几何体的三视图如图所示,其俯视图是由一个半圆与其直径 组成的图形,则此几何体的体积是( )A .B .C.D.10. 已知是内的一点,且,,若,和的面积分别为,则的最小值是( )A.B.C.D.11.如图,椭圆与双曲线有公共焦点、,它们在第一象限的交点为,且,,则椭圆与双曲线的离心率的倒数和为( )A.2B.C.D.12.已知函数, 则12340292015201520152015f f f f⎛⎫⎛⎫⎛⎫⎛⎫++++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的值为A.B.C.D.二、填空题:(本大题共4小题,每小题5分,满分20分)13.曲线在处的切线方程为_____________.14. 若满足且的最小值为,则的值为________.15. 已知三棱锥,,, 且,则三棱锥的外接球的表面积为________.16. .函数,,,,对任意的,总存在,使得成立,则的取值范围为.三、解答题(本大题共6小题,共70分)17.(本小题满分12分)设等差数列的前n项和为,数列的前n项和为满足(I)求数列的通项公式及数列的前n项和;(Ⅱ)是否存在非零实数,使得数列为等比数列?并说明理由18.(本小题满分12分)高三某班男同学有名,女同学有名,老师按照性别进行分层抽样组建了一个人的课外兴趣小组.(1)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出一名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;(2)试验结束后,第一次做试验的同学得到的试验数据为,第二次做试验的同学得到的试验数据为,请问哪位同学的实验更稳定?并说明理由.19.(本小题满分12分)如图,四棱锥,侧面是边长为的正三角形,且与底面垂直, 底面是的菱形,为的中点.(1) 在棱上是否存在一点,使得?若存在,指出点的位置并证明;若不存在,请说明理由; (2) 求点到平面的距离.20.(本小题满分12分) 已知圆:关于直线对称的圆为.(1)求圆的方程;(2)过点作直线与圆交于两点,是坐标原点.设,是否存在这样的直线,使得四边形的对角线相等?若存在,求出所有满足条件的直线的方程;若不存在,请说明理由.21.(本题满分12分) 设函数,.其中(1)设,求函数在上的值域;(2)证明:对任意正数,存在正数,使不等式成立.请考生从第(22)、(23)二题中任选一题作答。

河南省罗山县楠杆高中高三数学试题(文科)第1-7章第Ⅰ卷 共 60分一.选择题(5×12=60分)1.设命题p :{x | |x |>1};命题q :{x | x 2+ 2x –3>0},则p ⌝是q ⌝的( ) A .充分不必要条件 B .必要不充分条件C .充要条件 D .即不充分也不必要条件 2.若0a >,0b >,则以下不等式中不.恒成立的是( )A 、11()()4a b a b ++≥B 、3322a b ab +≥C 、22222a b a b ++≥+D 3.函数()3sin(2)3f x x π=-的图象为C ,如下结论中错误..的是( ) A. 图象C 关于直线1112x π=对称B. 图象C 关于点203π(,)对称 C. 函数()f x 在区间51212ππ(-,)内是增函数 D. 由3sin 2y x =的图象向右平移3π个单位长度可以得到图象C4.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若222()tan a c b B +-=,则角B 的值为( )A.6πB.3πC.6π或56πD.3π或23π5.将函数3log y x =的图像按向量a 平移后,得到函数32log 27x y +=的图像,则向量a =( )A. ()2,3 B. ()2,3- C ()2,3-- D. ()2,3-6.已知)(,n n n a a n a a -==+111,则数列{}n a 的通项公式=na ( )A. 12-nB. 11-+n n n )(C. 2n D. n7.设椭圆的两个焦点为F 1、F 2,如果过点F 1的直线被椭圆截得的最短线段MN 的长为532,且ΔMF 2N 的周长为20,则椭圆的离心率为 ( )A.522 B.517C.54D.538.已知数列4,,,121--a a 成等差数列, 4,,,1321--b b b 成等比数列,则212b a a -的值为( )A 、21 B 、—21 C 、21或—21 D 、41 9.在R 上定义运算).1(:y x y x -=⊗⊗若不等式1)()(<+⊗-a x a x 对任意实数x 成立,则( )A.11<<-aB.20<<aC.2321<<-a D.2123<<-a10.0)2(,0)(,0,),0)((=->'<∈≠f x f x R x x x f 且时当是奇函数,则不等式0)(>x f 的解集是( ) A .(—2,0) B .),2(+∞ C .),2()0,2(+∞- D .),2()2,(+∞--∞ 11.已知直线12:(3)(4)10,:2(3)230,l k x k y l k x y -+-+=--+=与平行,则k 得值是( )A. 1或3B.1或5C.3或5D.1或212.中心在原点,焦点在x 轴上的双曲线的实轴与虚轴相等,一个焦点到一条渐近线的距离为2,则双曲线方程为( )A .x 2-y 2=2 B .x 2-y 2=2 C . x 2-y 2=1 D .x 2-y 2=21第Ⅱ卷 共90分二.填空题(4×5=20)13.在锐角ABC ∆中,1,2,BC B A ==则cos AC A的值等于14.数列{a n }满足2112333 (32)n n na a a a -++++=,则n a =15.在平面直角坐标系xoy 中,已知△ABC 的顶点A (-4,0)和C(4,0),顶点B 在椭圆192522=+y x 上, 则=+BC A sin sin sin __ ____。

2021年高三上学期周考(12.20)考试数学试题含答案一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.i为虚数单位,,则z的共轭复数的虚部为()A.-iB. iC. -1D.12.若集合,,则()A. B. C. D.3.设,则“x<1”是“x≠2”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知函数y=2sinx的定义域为,值域为,则b-a的值不可能是()A. B. C. D.5.若某空间几何体的三视图如图所示,则该几何体的体积是()A.144B.48C.32D.166.设为抛物线上一点,F为抛物线C的焦点,以F为圆心,为半径的圆和抛物线的准线相交,则的取值范围是()A. B. C. D.7.x、y满足约束条件,若z=y-ax取得最大值的最优解不唯一,则实数a的值为()A.或-1B.2或C.2或1D.2或-18.已知,,则()A. B.-7 C. D.9.等差数列的前n项和为,且,,则过点和的直线的一个方向向量是()A. B. C. D.10.定义在上的函数f(x)满足下列两个条件:(1)对任意的恒有f(2x)=2f(x)成立;(2)当时,f(x)=2-x ;记函数g(x)=f(x)-k(x-1),若函数g(x)恰有两个零点,则实数k 的取值范围是() 14.2或-1 15. 16.1717.解:(1)∵,又根据余弦定理,∴22222cos 2cos 2c bc b A bc A bc c b ++=--+,化简得,可得,∵0<A<π,∴.(2)∵sinB+sinC=1,,,,,又∵B 为三角形内角,故,所以b=c=2,所以.18.解:(1)由题意知:的解集为,所以的根为-3,2,由韦达定理得a=6.(2)因为函数的定义域是,所以对恒成立,即对恒成立,所以. 又x a x x x a x x x x f x g -+=+-+=+=22212221log log )(log log )()(, g(x)的值域为,令,由题意知,的最小值为2,因为,所以当a=0时,t=x+1>1,无最小值,故a=0不成立,当a<0时,时,,所以,即.19.解:(1)∵,∴当时,,两式相减得,当n=1时,满足,则数列的通项公式为.(2),则前n 项和, 则,两式相减得112132212]212121[2212122222222121+-+--++⋅⋅⋅++=--+⋅⋅⋅+++=n n n n n n n n S 11112212)21(121212211])21(1[21221+-+----+=----⨯+=n n n n n n ,则. (3))32()12(1)12()12(1)32()12()12(4421+⋅+-+⋅-=+⋅+⋅-=⋅⋅++n n n n n n n a a a n n n , 则数列的前n 项和)32)(12(131)32)(12(1)12)(12(1751531531311++-=++-+-+⋅⋅⋅+⨯-⨯+⨯-⨯=n n n n n n T n . 20.(1)证明:在梯形ABCD 中,∵AB ∥CD ,AD=DC=CB=1,∠ABC=60°,∴AB=2,∴360cos 2222=⋅⋅-+=BC AB BC AB AC ,∴,∴BC ⊥AC ,∵平面ACFE ⊥平面ABCD ,平面ACFE 平面ABCD=AC ,BC 平面ABCD ,∴BC ⊥平面ACFE.(2)解:由(1)可建立分别以直线CA ,CB ,CF 为x 轴,y 轴,z 轴的如图所示的空间直角坐标系,令,则C(0,0,0),,B(0,1,0),,,设为平面MAB 的一个法向量,由得,取x=1,则,∵是平面FCB 的一个法向量,4)3(11)3(311cos 222121+-=⨯-++=⋅⋅=∴λλθn n n n ,∵,∴当时,有最小值,当时,有最大值,∴.21.解:(1)由题意可得,解得,∴椭圆的方程为.(2)易知直线l 斜率存在,令l :y=k(x+1),,,.联立,化为,.,,(※)∵,∴,可得,得.由,可得,可得得.)4)(1(8)(52)4)(1()1)(4()4)(1(222121222121+++++-=+++++++-=+∴x x x x x x x x x x x x μλ, 把(※)代入分子得,∴.22.解:(1),由题意:,解得,∴.(2)⎩⎨⎧-∈-+∈-+=-⋅+='⋅+=)1,1(),1)(()2,1[),1)((1)()()()(2222x x k x x x k x x k x x f k x x g ,.若在(-1,1)上有两根,且对恒成立.时,且时,,解得:.若在(-1,1)上有一根,且在上有一根,时,且时,,解得:.若在(-1,1)上恒成立,且对上有两根,而时,的对称轴为,所以不可能有两根,舍去.综上:或.eF30296 7658 癘35207 8987 覇22259 56F3 図20026 4E3A 为20835 5163 兣26808 68B8 梸26724 6864 桤23960 5D98 嶘t24129 5E41 幁p。

2021年高三上学期数学周练试卷(文科实验班12.29)含答案一、选择题(本大题共小题,每小题分,共5分在每个题给出的四个选项中,有且只有一项是符合题目要求的,请将答案填写在答卷纸上)1、过点(4,0)且斜率为的直线交圆于A,B两点,C为圆心,则的值为()A、6B、8C、D、42、已知数列{}为等差数列,是它的前n项和,若,,则=()A、32B、36C、40D、423、已知双曲线的一条渐近线方程是,则该双曲线的离心率等于()A、 B、C、 D、4、满足约束条件的目标函数的最大值是()A、-6B、e+1C、0D、e-15、设定义域为R的函数,则关于x的方程有5个不同的实数解,则=()A、B、C、2 D、16、点A是抛物线与双曲线的一条渐近线的交点(异于原点),若点A到抛物线的准线的距离为,则双曲线的离心率等于()A. B.2 C. D.47、已知符号函数,则函数的零点个数为()A.1 B.2 C.3 D.48、有下列命题:①在函数的图象中,相邻两个对称中心的距离为;②“且”是“”的必要不充分条件;③已知命题对任意的,都有,则“是:存在,使得”;④在中,若,则角等于或。
其中所有真命题的个数是()A.1 B.2 C.3 D.49.设集合,,函数若,且,则的取值范围是A.(]B. (]C. D .()10设集合A n ={x|(x -1)(x -n 2-4+ln n)<0},当n 取遍区间(1,3)内的一切实数,所有的集合A n 的并集是( )A .(1,13-ln 3)B .(1,6)C .(1,+∞)D .(1,2)二填空题(共6题,每题5分,共30分)11已知(1+x)+(1+x)2+…+(1+x)n =a 0+a 1x +a 2x 2+…+a n x n ,且a 1+a 2+…+a n -1=29-n ,则n =________12、早平面直角坐标系中中,直线是曲线的切线,则当时,实数的最小值是 -213、已知函数,。
2021年高三上学期第五次周考(文)数学试题含答案一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设为虚数单位,若复数,则等于()A.1 B. C. D.22. 已知下面四个命题:①“若,则或”的逆否命题为“且,则”②“”是“”的充分不必要条件A.1 B.2 C.3 D.43. 在等比数列中,,,,则等于()A. B. C. D.4.某程序框图如图所示,若输出的,则判断框内为()A. B. C. D.5. 在中,角所对的边分别为,若,则为()A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形6. 某几何体的三视图如图所示,则该几何体的侧面积等于()A. B. C. D.7. 已知平面上不重合的四点满足且,那么实数的值为()A.2 B.-3 C.4 D.58. 一只小蜜蜂在一个棱长为4的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个面的距离均大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为()A. B. C. D.9.关于的不等式在区间上有解,则实数的取值范围为()A. B. C. D.10.如图,椭圆的中心在坐标原点,焦点在轴上,为椭圆顶点,为右焦点,延长与交于点,若为钝角,则该椭圆离心率的取值范围是()A. B. C. D.11. 已知函数,则使得的的范围是()A. B. C. D.12. 定义在上的可导函数,当时,恒成立,,,,则的大小关系为()A. B. C. D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.对于实数和,定义运算,则式子的值为 .14.已知数的图象过点,令,,记数列的前项和为,则 .15.在西非肆虐的“埃博拉病毒”的传播速度很快,这已经成为全球性的威胁,为了考查某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:附表:参照附表,在犯错误的概率不超过(填百分比)的前提下,认为“小动物是否被感染与有没有服用疫苗有关”.16.已知函数与的图象上存在关于轴对称的点,则的取值范围是 .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)已知函数.(1)求函数的最小正周期;(2)将函数的图象向下平移个单位,再将图象上各点的纵坐标伸长到原来的2倍(横坐标不变),得到函数的图象,求使成立的的取值集合.18. (本小题满分12分)设数列的前项和为,已知.(1)求的值,并求数列的通项公式;(2)若数列为等差数列,且,,设,数列的前项和,证明:对任意,是一个与无关的常数.19. (本小题满分12分)如图1,在中,,,是上的高,沿将折成的二面角,如图2.(1)证明:平面平面;(2)设为的中点,,求异面直线和所成的角的大小.20. (本小题满分12分)已知抛物线的焦点为,直线与轴的交点为,与抛物线的交点为,且,已知椭圆的右焦点与抛物线的焦点重合,且离心率为.(1)求抛物线和椭圆的方程;(2)若过椭圆的右焦点的直线与椭圆交于两点,求三角形(为坐标原点)的面积的最大值.21. (本小题满分12分)已知函数.(1)求函数的单调区间;(2)若函数在区间上的最小值为0,求的值;(3)若对于任意,恒成立,求的取值范围.请考生在22、23中任选一题作答,如果多做,则按所做的第一题记分.22. (本小题满分10分)选修4-4:坐标系与参数方程已知曲线(为参数),(为参数).(1)化的方程为普通方程;(2)若上的点对应的参数为,为上的动点,求中点到直线(为参数)距离的最小值.23. (本小题满分10分)选修4-5:不等式选讲已知函数,,.(1)当时,若对任意恒成立,求实数的取值范围;(2)当时,求函数的最小值.参考答案 一、 选择题 CCDAA ABDAD AA 二、填空题 13.9 14. 15. 16.三、解答题17.解:(1)因为23131()cos (sin cos 2)sin cos cos 22f x x x x x x x =+=+ 31131111sin 2(1cos 2)(sin 2cos 2)sin(2)442224264x x x x x π=++=++=++所以,,故的取值集合为.18.解:(1)当时,,即,所以,因为,所以,两式相减,得,即,所以数列是首项为3,公比为3的等比数列,故.因为,则. 又,则.设的公差为,则,所以,所以由题意,则1232303(2)3(42)3n n T n =•+•+-•++-•234132303(2)3(62)3(42)3n n n T n n +=•+•+-•++-•+-•两式相减,得231223(2)3(2)3(2)3(42)3n n n T n +-=•+-•+-•++-•--•所以1119(13)1553(2)3()31322n n n n T n n -++-=-++-•=-+-•- 故为常数.19.解:(1)因为折起前是边上的高,则当折起后,,,又,则平面.因为平面,所以平面平面.(2)取的中点,连接,则,所以为异面直线与所成的角,连结,由,则,,,.在中,.在中,由题设,则2222cos 28BC BD CD BD CD BDC =+-••∠=,即, 从而,222cos 227BD BC CD CBD BD BC +-∠==•在中,2222cos 13DE BD BE BD BE CBD =+-•∠=,在中,.在中,,所以异面直线与所成的角的大小为.20.解:(1)设,代入抛物线方程中,得,∴,又,,∴,∴抛物线的方程为,在椭圆中,,∴,所以椭圆的标准方程为.(2)由题意可知,设直线的方程为,且,,由,得,,,2121211||||||22OAB S OF y y y y ∆=-=-==令,则,,又∵在上单调递增,∴,∴的最大值为.21.解:(1)当时,函数,在上单调递增,当时,,令,得,所以,当时,,函数单调递减;当时,,函数单调递增.(2)由(1)可知,当时,函数,不符合题意.当时,,因为,当时,,函数单调递减,当时,,函数单调递增.①当,即时,最小值为.解,得,符合题意.②当,即时,最小值为,解,得,不符合题意,综上,.(3)构建新函数,,①当,即时,因为,所以,(且时,仅当时,)所以在上单调递增,又,所以,当时,对于任意都有.②当时,解,即,得其中,,所以且,,所以在上单调递减.又,所以存在,使,不符合题意.综上,的取值范围为.22.(1)由,得,所以,由,得,所以(2)当时,,,故,为直线,到的距离4cos 3sin 13|5cos()13|513|d θθθϕ=--=+-≥-= (其中,)当且仅当时,取得最小值.23.解:(1)当时,,,当且仅当时等号成立,所以实数的取值范围是.(2)当时,12,01 ()22,122,2x xxg x x xx⎧+-<<⎪⎪=-≤≤⎨⎪>⎪⎩,当时,;当时,,当且仅当等号成立;故当时,函数取得最小值0.O 23877 5D45 嵅>K38080 94C0 铀{GC\27980 6D4C 浌35932 8C5C 豜7725132 622C 戬。
河南省部分重点高中2021届高三上学期质量检测数学(文科)考生注意:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
考试时间120分钟。
2.请将各题答案填写在答题卡上。
3.本试卷主要考试内容:高考全部内容。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={x |x ≤4x +5},B ={x |x 2<4},则A ∩B = A .{x |0<x <2} B .{x |-53≤x <2} C .{x |x ≥-53} D .{x |-2<x <2} 2.已知复数21212iz i i-+=+-+,则z 的共轭复数z =A .-1+iB .1+iC .1-iD .-1-i3.若向区域D ={(x ,y )|0≤x ≤1,0≤y ≤1}内随机投点,则该点落在区域{(x ,y )|x 2+y 2≤14}内的概率为 A .4π B .8π C .16π D .32π4.若x ,y 满足约束条件2201020x y x y y ⎧⎪⎨⎪⎩+-≤,--≥,+≥,则z =4x +y 的最大值为 A .2 B .4 C .6 D .85.正多面体被古希腊圣哲认为是构成宇宙的基本元素,加上它们的多种变体,一直是科学、艺术、哲学灵感的源泉之一.如图,该几何体是一个棱长为2的正八面体,则此正八面体的体积与表面积之比为A .6 B .6 C .6 D .6 6.已知α∈(0,π),且2cos22cos cos ααα=-,则sin α=A .23 B .23 C .13D .2237.设O为坐标原点,直线x=a与双曲线C:22221x ya b-=(a>0,b >0)的两条渐近线分别交于D,E两点.若C的焦距为4,则△ODE面积的最大值为A.1 B.2 C.4 D.88.下图是某算法的程序框图,则程序运行后输出的结果是A.4 B.5 C.6 D.79.已知A,B分别为椭圆22221x ya b+=(a>b>0)的左、右顶点,P,Q是椭圆上的不同两点且关于x轴对称,设直线AP,BQ的斜率分别为m,n,若mn=14,则该椭圆的离心率为A.63B.22C.32D.2310.已知函数()()sinf x xωϕ=+(ω>0,|ϕ|<2π)的部分图象如图所示,则A.ω=3B.ϕ=6πC.f(0)+f(6π)+f(26π)+f(36π)+f(46π)+…+f(20196π)=0D.f(6π)+f(26π)+f(36π)+f(46π)+…+f(20196π)=011.已知二次函数f(x)满足f(x+1)=f(x)-2x+1,且f(1)=-1.对任意x1>x2>-1,()()1212f x f xx x-->m(x1+x2)成立,则m的取值范围为A.[-2,-1] B.[-2,-1)C.[-4,-1] D.[-4,-1)12.设函数()ln xf xx=,若存在[a,b] ⊆[1e,e],使得f(x)在[a,b]上的值域为[ka,kb],则实数k的取值范围为A.[21e,12e)B.[21e,1)C.[12e,1e)D.[12e,1)第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上. 13.已知平面向量a =(1,m ),b =(m -1,-3),且a ·b =|a |,则m =__________. 14.定义在R 上的奇函数f (x )在[0,+∞)上是减函数,若f (m )+f (3-2m )>f (0),则m 的取值范围为__________. 15.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,A =4π,csin A =4sin C ,若此三角形有两解,则b 的取值范围是__________.16.如图,在四棱锥P —ABCD 中,PA ⊥平面ABCD ,若PA =AD =2,AD∥BC ,∠DAB =∠ADC =3π,PC 与平面ABCD 所成角的正切值为233,则四棱锥P —ABCD 外接球的表面积为__________.三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.(一)必考题:共60分. 17.(12分)为了解某农场的种植情况,该农场的技术人员对种植出来的水果进行抽样检测,将测得的水果重量分成[15.5,16.5), [16.5,17.5),[17.5,18.5),[18.5,19.5),[19.5,20.5), [20.5,21.5]六组进行统计,得到如图所示的统计图. (1)估计该农场的水果重量的平均数(同一组当中的水果重量用该组的中间值代替); (2)从样本中重量不小于19.5克的水果中任取2个,求至少有1个水果的重量不小于20.5克的概率. 18.(12分) 已知数列{n a }的首项为12,且满足()()111n n n a n a -+=-(n ≥2,n N *∈). (1)求{n a }的通项公式; (2)已知n b =n a +1nna ,求数列{n b }的前n 项和n S . 19.(12分)如图,在四面体ABCD 中,△ABD 是等边三角形,且AC =BC . (1)证明:AB ⊥CD .(2)若AB =2,AC,BC ⊥CD ,求点B 到平面ACD 的距离.20.(12分)已知动点M 到点F (3,0)的距离比它到直线l :x +5=0的距离小2. (1)求动点M 的轨迹E 的方程.(2)过点F 作斜率为k (k ≠0)的直线l '与轨迹E 交于点A ,B ,线段AB 的垂直平分线交x 轴于点N ,证明:ABFN为定值.21.(12分)已知函数f (x )=alnx -x . (1)讨论函数f (x )的单调性;(2)若不等式f (x )≥(e -1)x -e x 对x ∈[1,+∞)恒成立,求a 的取值范围. (二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.[选修4—4:坐标系与参数方程](10分)在直角坐标系xOy 中,直线l 的参数方程为1232x t y t⎧⎨⎩=+,=-(t 为参数),曲线C 的方程为x 2-4x +y 2+2=0,以O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求直线l 和曲线C 的极坐标方程;(2)若射线θ=α(0<α<2π)与曲线C 相切于点M (点M 位于第一象限),且与直线l 相交于点N ,求|MN |.23.[选修4—5:不等式选讲](10分)已知正实数a ,b ,c 满足ab +bc +ac =abc . (1)证明:a +b +c ≥9. (2)证明:222b c aa b c ++≥1.。
2021年高三上学期第五次模拟数学试卷(文科)含解析一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的).B=()1.已知全集为R,集合A={x|2x≥1},B={x|x2﹣3x+2≤0},则A∩∁RA.{x|x≤0} B.{x|1≤x≤2} C.{x|0≤x<1或x>2} D.{x|0≤x<1或x≥2}2.已知复数(x﹣2)+yi(x,y∈R)的模为,则的最大值是()A.B.C.D.3.设0<x<,记a=lnsinx,b=sinx,c=e sinx,则比较a,b,c的大小关系为()A.a<b<c B.b<a<c C.c<b<a D.b<c<a4.如图(1)、(2)、(3)、(4)为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为()A.三棱台、三棱柱、圆锥、圆台B.三棱台、三棱锥、圆锥、圆台C.三棱柱、正四棱锥、圆锥、圆台D.三棱柱、三棱台、圆锥、圆台5.设α、β、γ为平面,m、n、l为直线,则m⊥β的一个充分条件是()A.α⊥β,α∩β=l,m⊥l B.α∩γ=m,α⊥γ,β⊥γC.α⊥γ,β⊥γ,m⊥αD.n⊥α,n⊥β,m⊥α6.已知α是第二象限角,其终边上一点,且cosα=x,则=()A. B. C. D.7.若函数f(x)=x2+2x+alnx在(0,1)上单调递减,则实数a的取值范围是()A.a≥0 B.a≤0 C.a≥﹣4 D.a≤﹣48.设A,B,C是△ABC三个内角,且tanA,tanB是方程3x2﹣5x+1=0的两个实根,那么△ABC 是()A.钝角三角形B.锐角三角形C.等腰直角三角形D.以上均有可能9.已知数列{a n}是等差数列,其前n项和为S n,若首项a1>0且,有下列四个命题:P1:d<0;P2:a1+a10<0;P3:数列{a n}的前5项和最大;P4:使S n>0的最大n值为10;其中正确的命题个数为()A.1个B.2个C.3个D.4个10.已知数列{a n}(n=1,2,3,…,xx),圆C1:x2+y2﹣4x﹣4y=0,圆C2:x2+y2﹣2a n x﹣2a xxy=0,若圆C2平分圆C1的周长,则{a n}的所有项的和为()﹣nA.4028 B.4026 C.xx D.xx11.双曲线﹣=1的右焦点F与抛物线y2=2px(p>0)的焦点重合,且在第一象限的交点为M,MF直于x轴,则双曲线的离心率是()A.2+2 B.2 C. +1 D. +212.对任意实数a,b定义运算“⊗”:,设f(x)=(x2﹣1)⊗(4+x),若函数y=f(x)+k的图象与x轴恰有三个不同交点,则k的取值范围是()A.(﹣2,1)B. C. C.+(1+2+4+…+2n﹣1)==(n2+2n)+(2n﹣1)=2n+n2+2n﹣1.所以数列{c n}的前n项和T n为2n+n2+2n﹣1.18.某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:日期1月10日2月10日3月10日4月10日5月10日6月10日昼夜温差x(°C)10 11 13 12 8 6就诊人数y(个)22 25 29 26 16 12该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.(Ⅰ)求选取的2组数据恰好是相邻两个月的概率;(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程=bx+a;(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?(参考公式:b==,a=﹣b)【考点】线性回归方程.【分析】(Ⅰ)本题是一个古典概型,试验发生包含的事件是从6组数据中选取2组数据共有C62种情况,满足条件的事件是抽到相邻两个月的数据的情况有5种,根据古典概型的概率公式得到结果.(Ⅱ)根据所给的数据,求出x,y的平均数,根据求线性回归方程系数的方法,求出系数b,把b和x,y的平均数,代入求a的公式,做出a的值,写出线性回归方程.(Ⅲ)根据所求的线性回归方程,预报当自变量为10和6时的y的值,把预报的值同原来表中所给的10和6对应的值做差,差的绝对值不超过2,得到线性回归方程理想.【解答】解:(Ⅰ)由题意知本题是一个古典概型,设抽到相邻两个月的数据为事件A,试验发生包含的事件是从6组数据中选取2组数据共有C62=15种情况,每种情况都是等可能出现的其中,满足条件的事件是抽到相邻两个月的数据的情况有5种,∴P(A)==;(Ⅱ)由数据求得=11, =24,由公式求得===,再由=﹣b,求得=﹣,∴y关于x的线性回归方程为=x﹣,(Ⅲ)当x=10时, =,|﹣22|=<2,当x=6时, =,|﹣12|=<2,∴该小组所得线性回归方程是理想的.19.如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=,O为AC与BD的交点,E为棱PB上一点.(Ⅰ)证明:平面EAC⊥平面PBD;(Ⅱ)若PD∥平面EAC,求三棱锥P﹣EAD的体积.【考点】棱柱、棱锥、棱台的体积;平面与平面垂直的判定.【分析】(Ⅰ)由已知得AC⊥PD,AC⊥BD,由此能证明平面EAC⊥平面PBD.(Ⅱ)由已知得PD∥OE,取AD中点H,连结BH,由此利用,能求出三棱锥P﹣EAD的体积.【解答】(Ⅰ)证明:∵PD⊥平面ABCD,AC⊂平面ABCD,∴AC⊥PD.∵四边形ABCD是菱形,∴AC⊥BD,又∵PD∩BD=D,AC⊥平面PBD.而AC⊂平面EAC,∴平面EAC⊥平面PBD.(Ⅱ)解:∵PD∥平面EAC,平面EAC∩平面PBD=OE,∴PD∥OE,∵O是BD中点,∴E是PB中点.取AD中点H,连结BH,∵四边形ABCD是菱形,∠BAD=60°,∴BH⊥AD,又BH⊥PD,AD∩PD=D,∴BD⊥平面PAD,.∴==.20.如图,椭圆C: +=1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,且|AB|=|BF|.(Ⅰ)求椭圆C的离心率;(Ⅱ)若斜率为2的直线l过点(0,2),且l交椭圆C于P、Q两点,OP⊥OQ.求直线l的方程及椭圆C的方程.【考点】直线与圆锥曲线的综合问题.【分析】(Ⅰ)利用|AB|=|BF|,求出a,c的关系,即可求椭圆C的离心率;(Ⅱ)直线l的方程为y﹣2=2(x﹣0),即2x﹣y+2=0与椭圆C:联立,OP⊥OQ,可得,利用韦达定理,即可求出椭圆C的方程.【解答】解:(Ⅰ)由已知,即,4a2+4b2=5a2,4a2+4(a2﹣c2)=5a2,∴.…(Ⅱ)由(Ⅰ)知a2=4b2,∴椭圆C:.设P(x1,y1),Q(x2,y2),直线l的方程为y﹣2=2(x﹣0),即2x﹣y+2=0.由,即17x2+32x+16﹣4b2=0..,.…∵OP⊥OQ,∴,即x1x2+y1y2=0,x1x2+(2x1+2)(2x2+2)=0,5x1x2+4(x1+x2)+4=0.从而,解得b=1,∴椭圆C的方程为.…21.已知函数f(x)=e x﹣x2+a,x∈R的图象在点x=0处的切线为y=bx.(e≈2.71828).(Ⅰ)求函数f(x)的解析式;(Ⅱ)当x∈R时,求证:f(x)≥﹣x2+x;(Ⅲ)若f(x)>kx对任意的x∈(0,+∞)恒成立,求实数k的取值范围.【考点】利用导数研究曲线上某点切线方程;利用导数求闭区间上函数的最值.【分析】(Ⅰ)利用图象在点x=0处的切线为y=bx,求出a,b,即可求函数f(x)的解析式;(Ⅱ)令φ(x)=f(x)+x2﹣x=e x﹣x﹣1,确定函数的单调性,可得φ(x)min=φ(0)=0,即可证明:f(x)≥﹣x2+x;(Ⅲ)f(x)>kx对任意的x∈(0,+∞)恒成立对任意的x∈(0,+∞)恒成立,k<g(x)min=g(1)=0,即可求实数k的取值范围.【解答】解:(Ⅰ)f(x)=e x﹣x2+a,f'(x)=e x﹣2x.由已知,f(x)=e x﹣x2﹣1.…(Ⅱ)令φ(x)=f(x)+x2﹣x=e x﹣x﹣1,φ'(x)=e x﹣1,由φ'(x)=0,得x=0,当x∈(﹣∞,0)时,φ'(x)<0,φ(x)单调递减;当x∈(0,+∞)时,φ'(x)>0,φ(x)单调递增.∴φ(x)min=φ(0)=0,从而f(x)≥﹣x2+x.…(Ⅲ)f(x)>kx对任意的x∈(0,+∞)恒成立对任意的x∈(0,+∞)恒成立,令,∴.由(Ⅱ)可知当x∈(0,+∞)时,e x﹣x﹣1>0恒成立,…令g'(x)>0,得x>1;g'(x)<0,得0<x<1.∴g(x)的增区间为(1,+∞),减区间为(0,1).g(x)min=g(1)=0.∴k<g(x)min=g(1)=e﹣2,∴实数k的取值范围为(﹣∞,e﹣2).…请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请在答题卡上填涂题号对应标记.选修4-1:几何证明选讲22.如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC 边的中点,连接OD交圆O于点M.(1)求证:O、B、D、E四点共圆;(2)求证:2DE2=DM•AC+DM•AB.【考点】与圆有关的比例线段.【分析】(1)连接BE、OE,由直径所对的圆周角为直角,得到BE⊥EC,从而得出DE=BD=,由此证出△ODE≌△ODB,得∠OED=∠OBD=90°,利用圆内接四边形形的判定定理得到O、B、D、E四点共圆;(2)延长DO交圆O于点H,由(1)的结论证出DE为圆O的切线,从而得出DE2=DM•DH,再将DH分解为DO+OH,并利用OH=和DO=,化简即可得到等式2DE2=DM•AC+DM•AB成立.【解答】解:(1)连接BE、OE,则∵AB为圆0的直径,∴∠AEB=90°,得BE⊥EC,又∵D是BC的中点,∴ED是Rt△BEC的中线,可得DE=BD.又∵OE=OB,OD=OD,∴△ODE≌△ODB.可得∠OED=∠OBD=90°,因此,O、B、D、E四点共圆;(2)延长DO交圆O于点H,∵DE⊥OE,OE是半径,∴DE为圆O的切线.可得DE2=DM•DH=DM•(DO+OH)=DM•DO+DM•OH.∵OH=,OD为△ABC的中位线,得DO=,∴,化简得2DE2=DM•AC+D M•AB.选修4-4:极坐标系与参数方程23.在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为.(Ⅰ)求圆C的圆心到直线l的距离;(Ⅱ)设圆C与直线l交于点A、B.若点P的坐标为(3,),求|PA|+|PB|.【考点】直线的参数方程;简单曲线的极坐标方程.【分析】(I)圆C的极坐标方程两边同乘ρ,根据极坐标公式进行化简就可求出直角坐标方程,最后再利用三角函数公式化成参数方程;(Ⅱ)将直线l的参数方程代入圆C的直角坐标方程,得即,根据两交点A,B所对应的参数分别为t1,t2,利用根与系数的关系结合参数的几何意义即得.【解答】解:(Ⅰ)由,可得,即圆C的方程为.由可得直线l的方程为.所以,圆C的圆心到直线l的距离为.…(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得,即.由于△=.故可设t1、t2是上述方程的两个实根,所以,又直线l过点,故由上式及t的几何意义得.…选修4-5:不等式选讲24.已知函数f(x)=|2x+1|+|2x﹣3|.(Ⅰ)求不等式f(x)≤6的解集;(Ⅱ)若关于x的不等式f(x)<|a﹣1|的解集非空,求实数a的取值范围.【考点】带绝对值的函数;其他不等式的解法.【分析】(Ⅰ)不等式等价于①,或②,或③.分别求出这3个不等式组的解集,再取并集,即得所求.(Ⅱ)由绝对值不等式的性质求出f(x)的最小值等于4,故有|a﹣1|>4,解此不等式求得实数a的取值范围.【解答】解:(Ⅰ)不等式f(x)≤6 即|2x+1|+|2x﹣3|≤6,∴①,或②,或③.解①得﹣1≤x<﹣,解②得﹣≤x≤,解③得<x≤2.故由不等式可得,即不等式的解集为{x|﹣1≤x≤2}.(Ⅱ)∵f(x)=|2x+1|+|2x﹣3|≥|(2x+1)﹣(2x﹣3)|=4,即f(x)的最小值等于4,∴|a﹣1|>4,解此不等式得a<﹣3或a>5.故实数a的取值范围为(﹣∞,﹣3)∪(5,+∞).xx年8月4日\25147 623B 戻23445 5B95 宕g21490 53F2 史 20597 5075 偵22999 59D7 姗20766 511E 儞21575 5447 呇33099 814B 腋$ 33015 80F7 胷24700 607C 恼。
2021年高三上学期第五次模拟考试数学(文)试题含答案赵晓玲杨丽芬 xx年4月本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~24题为选考题,其它题为必考题。
第Ⅰ卷(选择题)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集为,集合A,,则A. B. C. D.2.设i是虚数单位,复数z=的值是A. B. C. D.13.若是真命题,是假命题,则A.是真命题B.是假命题C.是真命题D.是真命题4.某程序框图如图2所示,现将输出值依次记为:若程序运行中输出的一个数组是则数组中的A.32 B.24C.18 D.165.设,,,则A. B. C. D.6.下列函数中,最小正周期为,且图象关于直线对称的是A.B.C.D.7.为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:做不到“光盘”能做到“光盘”男45 10附:参照附表,得到的正确结论是A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”8.定义在R上的奇函数满足,且在上是增函数,则有A.B.C.D.9.如图,在4,30,ABC AB BC ABC AD∆==∠=中,是边BC上的高,则的值等于A.0 B.4 C.8 D.10.若,,,则下列不等式中:①;②;③;④.对一切满足条件的,恒成立的序号是A.①②B.①③C.①③④D.②③④11.已知双曲线的左、右焦点分别是,正三角形的一边与双曲线左支交于点,且,则双曲线的离心率的值是A.B.C.D.12.已知函数,且,则当时,的取值范围是A.B.C.D.第Ⅱ卷(非选择题)二、填空题:本大题共4小题,每小题5分,共20分。