下载文档原格式
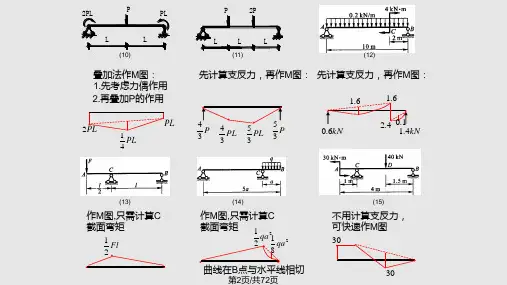
分段叠加法作弯矩图
作弯矩图时，可采用叠加法，使绘制工作得到简化。
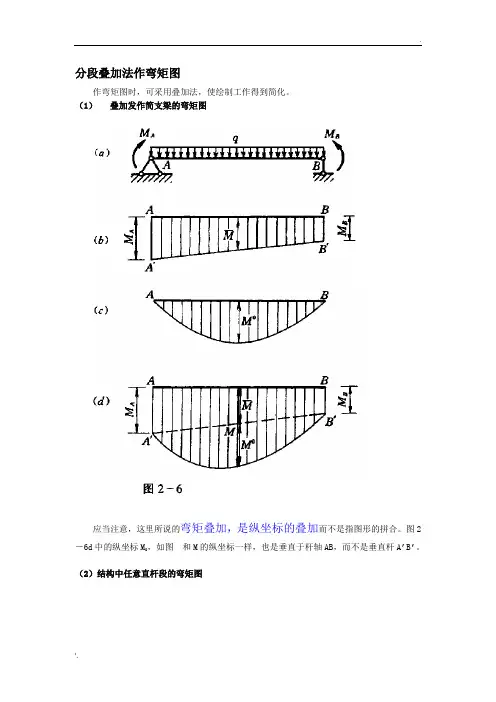
（1）叠加发作简支梁的弯矩图
应当注意，这里所说的弯矩叠加，是纵坐标的叠加而不是指图形的拼合。
图2－6d中的纵坐标M0，如图和M的纵坐标一样，也是垂直于杆轴AB，而不是垂直杆A’B’。
（2）结构中任意直杆段的弯矩图
结论：任意直杆段的弯矩图的特性和与其相应的（长度、承受荷载q和两端弯矩M A、M B均相同）简支梁的竖向力Y A、Y B（Y0A、Y0B）和弯矩图完全相同，因此，我们可以用前面所属的叠加法来绘制任意直杆段的弯矩图。
具体作法如下：先求出杆段两端截面的弯矩图M A、M B。
作直线的图，然后依此直线为基线，叠加相应简支梁在跨间荷载作用下的M0图（如d所示）
小结：梁弯矩图的一般作法
利用内力图的特性和弯矩图叠加法，将梁弯矩图的一般作法归纳如下：
（1）选定外力的不连续点（如集中力、集中力偶的作用点，分布力的起点和终点等）为控制截面，求出任制裁面的弯矩值。
（2）分段画弯矩图。
当控制截面之间无荷载时，该段弯矩图是直线图形。
当控制截面之间
有荷载时，用叠加法作该段的弯矩图。
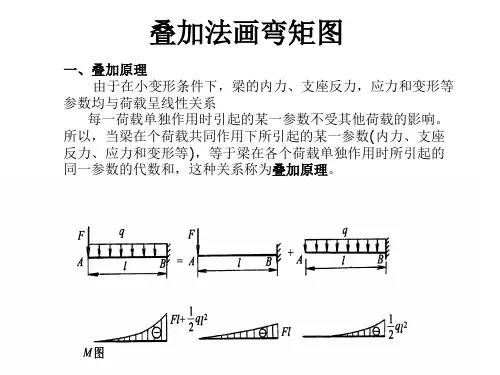
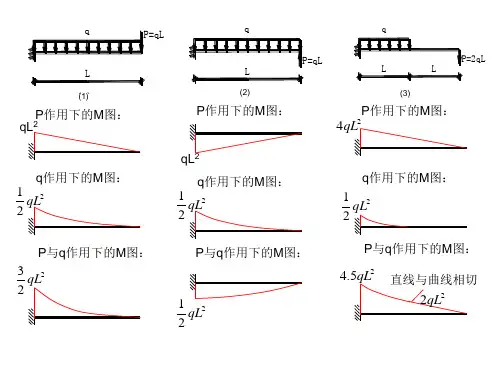
2．6叠加法作弯矩图当梁在荷载作用下变形微小，因而在求梁的支反力、剪力、弯矩时可直接代入梁的原始尺寸进行计算，且所得结果与梁上荷载成正比。
在这种情况下，当梁上有几项荷载作用时，由每一项荷载所引起的梁的支反力或内力，将不受其他荷载的影响。
所以在计算梁的某截面上的弯矩时，只需先分别算出各项荷载单独作用时在该截面上引起的弯矩，然后求它们的代数和即得到该截面上的总弯矩。
这种由几个外力共同作用引起的某一参数(内力、位移等)等于每一外力单独作用时引起的该参数值的代数和的方法，称为叠加法。
叠加法的应用很广，它的应用条件是：需要计算的物理量(如支反力、内力以及以后要讨论的应力和变形等)必须是荷载的线性齐次式。
也就是说，该物理量的荷载表达式中既不包含荷载的一次方以上的项，也不包含荷载的零次项。
例题2-9试按叠加原理做例题2-9图(a)所示简支梁的弯矩图。
求梁的极值弯矩和最大弯矩。
解：先将梁上每一项荷载分开(见图(b)、图(c))，分别做出力偶和均布荷载单独作用的弯矩图(见图(d)、图(e))两图的纵坐标具有不同的正负号，在叠加时可把它们画在x 轴同一侧(见图f)。
于是两图共有部分，其正、负纵坐标值互相抵消。
剩下的纵距(见图(f)中阴影线部分)即代表叠加后的弯矩值。
叠加后的弯矩图仍为抛物线。
如将它改画为以水平直线为基线的图，即得通常形式的弯矩图(见图(曲)。
求极值弯矩时，先要确定剪力为零的截面位置。
由平衡方程0Bm =∑可求得支反,剪力方程为Q 即可求出极值弯矩所在截面的位置。
令()0x极值弯矩为由例题2-9图（g)可见，全梁最大弯矩为本例中的极值弯矩并不大于梁的最大值弯矩。
当梁上的荷载较复杂时，也可将梁按荷载情况分段，求出每一段梁两端截面的内力。
这时该段梁的受载情况等效于一受相同荷载的简支梁 (见图2-12(a)、(b))。
因为每一段梁在平面弯曲时的内力，不外是轴力N、剪力Q和弯矩M。
由于轴力N不产生弯矩，故在作弯矩图时可将它略去，剩下的梁端剪力1Q，2Q和梁端弯矩1M、2M，及荷载对梁段的作用，可用图2-12(b)所示的简支梁上相应的荷载来代替(梁段端截面上的剪力可由梁的支反力提供，故图中未画出)。
