高阶谱分析及其应用

第1章 高阶统计量的定义与性质1.1 准备知识1. 随机变量的特征函数若随机变量x 的分布函数为)(x F ，则称⎰⎰∞∞-∞∞-===Φdx x f e x dF e e E x j x j x j )()(][)(ωωωω为x 的特征函数。

其中)(x f 为概率密度函数。

离散情况：}{,][)(k k k kx j x j x x p p p e e E k ====Φ∑ωωω特征函数)(ωΦ是概率密度)(x f 的付里叶变换。

例：设x ~),(2σa N ，则特征函数为dx e e x j a x ⎰∞∞---=Φωσσπω222/)(21)(令σ2/)(a x z -=，则dz e aj z j z⎰∞∞-++-=Φωσωπω221)(根据公式：AB AC CxBx AxeAdx e 222--∞∞--±-=⎰π，则 2221)(σωωω-=Φa j e若0=a ，则2221)(σωω-=Φe。

2. 多维随机变量的特征函数设随机变量n x x x ,,,21 联合概率分布函数为),,,(21n x x x F ，则联合特征函数为),,,(][),,,(21)()(2122112211n x x x j x x x j n x x x dF e eE n n n n ⎰⎰∞∞-+++∞∞-+++==Φωωωωωωωωω令T n x x x ],,,[21 =x ,T n ],,,[21ωωω =ω，则⎰=ΦdX f e Tj )()(x ωx ω 矩阵形式或 n n x jn dx dx x x f eknk k ,,),,(),,,(11211⎰⎰∞∞-∞∞-∑=Φ=ωωωω 标量形式其中，),,,()(21n x x x f f =x 为联合概率密度函数。

例：设n 维高斯随机变量为T n x x x ],,,[21 =x ,T n a a a ],,,[21 =a⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=nn n n n c c c c c c2111211c )])([(],cov[k k i i k i ik a x a x E x x c --== x 的概率密度为⎭⎬⎫⎩⎨⎧---=)()(21exp )2(1)(2/12/a x c a x cx T n P π x 的特征函数为⎭⎬⎫⎩⎨⎧-=Φc ωωωa ωT T j 21ex p )( 矩阵形式其中，T n ],,,[21ωωω =ω,⎭⎬⎫⎩⎨⎧-=Φ∑∑∑===n i nj j i ij ni i i n C a j 1112121exp ),,,(ωωωωωω 标量形式 3. 随机变量的第二特征函数定义：特征函数的对数为第二特征函数为 )(ln )(ωωΦ=ψ (1) 单变量高斯随机过程的第二特征函数 22221ln )(22σωωωσωω-==ψ-a j e a j(2) 多变量情形j n i i nji ij i ni i n C a j ωωωωωω∑∑∑===-=ψ1112121),,,(1.2 高阶矩与高阶累积量定义1. 单个随机变量情形 (1) 高阶矩定义随机变量x 的k 阶矩定义为⎰∞∞-==dx x p x x E m k k k )(][ (1.1)显然10=m ，][1x E m ==η。

高阶谱分析Higher-Order Spectra Analysis第一章 绪论在过去的30多年中，由于系统理论、统计学、数值分析、计算机科学和集成电路技术等领域思想与方法的结合使信号处理特别是数字信号处理有了巨大的发展。

传统信号处理的主要特点是研究线性的（Linear）、因果的(Causal)、最小相位的(Minimum phase)、高斯分布的(Gaussian)、平稳的(Stationary)和整数维(Integer dimensional)的信号分析与综合。

现代信号处理的特点是注重研究非线性的(Non-linear)、非因果的(Non-causal)、非最小相位(Non-minimum phase)信号与系统，以及非高斯的(Non-Gaussian)、非平稳的(Non-stationary)和分形(Fractional)（非整数维）信号和非白色(Color)的加性(Additive)噪声。

信号处理的目的：处理有限个数据样本，并从中提取隐藏在这些数据中的重要信息。

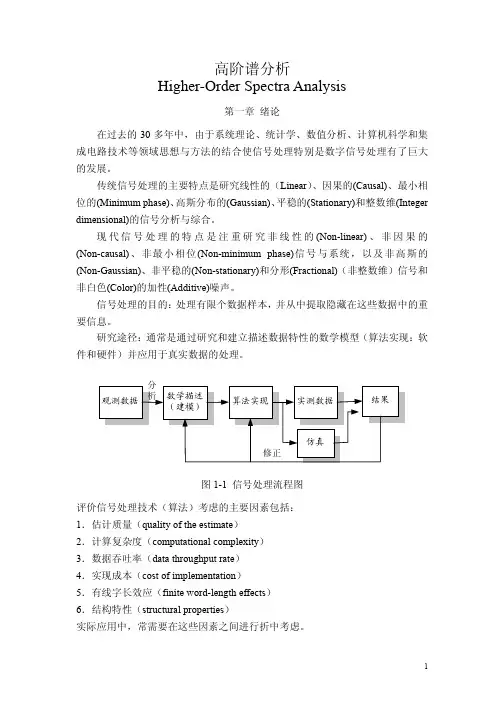
研究途径：通常是通过研究和建立描述数据特性的数学模型（算法实现：软件和硬件）并应用于真实数据的处理。

图1-1 信号处理流程图评价信号处理技术（算法）考虑的主要因素包括：1．估计质量（quality of the estimate）2．计算复杂度（computational complexity）3．数据吞吐率（data throughput rate）4．实现成本（cost of implementation）5．有线字长效应（finite word-length effects）6．结构特性（structural properties）实际应用中，常需要在这些因素之间进行折中考虑。

1.1 功率谱（Power Spectrum ）功率谱密度（PSD: Power Spectrum Density ）是数字信号处理中的一种常用技术。

cpm 高阶谱离散谱线CPM高阶谱和离散谱线是在频域分析方法中所经常使用的概念。

本文主要介绍这两个概念的基本概念和应用。

CPM高阶谱CPM高阶谱是一种高阶谱分析方法，也称为三次非线性波互模色散相位匹配（CPM）分析。

这种方法是通过非线性的光学效应来分析光学系统。

CPM方法是一种考虑非线性相互作用的高阶频谱分析技术。

它可以提供比简单二次谱分析更细致的谱范围，使得我们可以对系统的特定频率响应进行更准确的分析。

CPM高阶谱可用于分析许多不同类型的系统，包括分散介质中的光纤、非线性光学晶体和非线性光学波导器件等。

这种方法利用所谓的相位匹配条件来确定非线性频率转换过程的发生条件。

相位匹配条件是可以使用非线性谐波产生的相位偏差来描述的。

CPM高阶谱可以提供非常精确的相位匹配条件，因此可以用于分析非常复杂的光学系统。

离散谱线离散谱线是一种用于描述系统频率响应的频谱分析方法。

离散谱线可以用于分析任意类型的动态系统，包括机械，电子和光学系统。

离散谱线通过离散计算频率响应函数来分析系统，然后将其变换为离散谱线。

离散谱线通过将一个复杂的系统分解成许多单独的分量来工作。

这些分量被处理为离散频率响应函数，并被处理为离散谱线形式。

这种方法可以提供非常精细的频率响应分析，可以用于调制和滤波器设计。

离散谱线可以帮助我们了解系统如何受到不同频率成分的影响，并有助于优化系统设计。

它们也可以用于预测系统响应，从而进行故障诊断和修复。

虽然离散谱线方法在理论上比较复杂，但它们在实际系统设计中已经广泛应用，因为它们可以提供非常精确的预测结果。

结论CPM高阶谱和离散谱线是频域分析中最常用的方法之一。

这些方法利用非线性建模和离散频率响应函数来提供精确的频率响应分析。

虽然这些方法需要一定的数学和物理背景知识，但它们已经在各种系统领域的应用中证明了它们的效用和精度。

一种基于高阶谱特征的舰船目标识别方法随着现代军事技术的快速发展，舰船目标识别已经成为了军事领域的重要研究内容。

通过对舰船目标进行快速准确识别，可以有效提高军事作战的效率，保障国家安全。

在众多舰船目标识别方法中，基于高阶谱特征的方法具有较高的效率和准确性。

一种基于高阶谱特征的舰船目标识别方法，首先需要对舰船目标的信号进行预处理，以得到干净稳定的信号。

其次，利用高阶谱特征分析舰船目标信号，得到高阶谱密度函数。

高阶谱密度函数是一种反映信号在时频二维平面内的时频分布信息的特征函数，可以有效减少噪声和干扰的影响。

其次，通过对高阶谱密度函数的研究，建立舰船目标的特征集合。

特征集合包括频率信息、时序信息、能量信息等多种特征。

最后，通过对舰船目标信号的特征集合进行分类分析，得出舰船目标识别结果。

基于高阶谱特征的舰船目标识别方法具有多个优点。

首先，高阶谱特征能够提取舰船目标的多维特征信息，准确地反映信号的动态特性。

其次，该方法能够显著降低噪声和有害干扰的影响。

其次，该方法不需要对信号进行假设，不受信号模型复杂度的限制，具有较高的适应性。

最后，该方法具有较高的准确性和稳定性，能够有效识别目标并防止误判。

然而，基于高阶谱特征的舰船目标识别方法也存在一些不足。

首先，该方法需要较高的计算复杂度，对硬件要求较高。

其次，对于复杂纹理、变形较大的目标，该方法的检测效率较低。

最后，该方法对噪声和干扰的处理依然存在一定局限性。

综上所述，基于高阶谱特征的舰船目标识别方法具有诸多优点与不足。

在采用该方法时应考虑具体情况，根据实际应用需求进行选择。

同时，该方法也为舰船目标的快速准确识别提供了一种新的思路，为研究舰船目标识别提供了新的思路和方法。

数据是分析问题和制定合理决策的基础，在舰船目标识别研究中，收集和分析相关数据也十分重要。

下面将列出一些相关数据并进行简单的分析。

1. 舰船目标的外形尺度参数，包括长度、宽度、高度等数据。

这些数据可以用于建立目标的基本特征，帮助识别舰船目标。

机械工程中机械振动信号的谱分析与识别机械振动信号的谱分析与识别引言机械工程中，机械振动信号的谱分析与识别是一个重要的研究领域。

振动信号可以提供机械设备的状态信息，通过对振动信号的谱分析和识别，可以检测出机械设备的故障，并进行预测与维护。

本文将介绍机械振动信号的谱分析方法、振动信号的特征提取以及故障诊断等相关内容。

一、机械振动信号的谱分析方法谱分析是对信号进行频域分析的方法。

在机械振动信号的谱分析中，常用的方法有傅里叶变换、小波变换和高阶谱分析等。

1. 傅里叶变换傅里叶变换是将时域信号转换为频域信号的数学工具，可以将信号分解为不同频率的正弦和余弦函数。

通过傅里叶变换，可以得到振动信号的频谱信息，从而分析机械系统的振动特性。

2. 小波变换小波变换是一种时频分析方法，可以同时提供时域和频域的信息。

相比于傅里叶变换，小波变换可以更好地分析非平稳信号的频谱特性。

在机械振动信号的谱分析中，小波变换常用于检测故障频率和跟踪频率的变化。

3. 高阶谱分析高阶谱分析是对信号进行高阶统计处理的方法，可以提供更多关于信号的非线性和非高斯特性的信息。

在机械振动信号的谱分析中，高阶谱分析常用于检测非线性振动和故障特征。

二、振动信号的特征提取振动信号的特征提取是将信号的频谱信息转化为能够描述机械系统状态的特征量。

常用的特征包括有效值、峰值、峰峰值、均方根值、偏度、峭度等。

1. 有效值有效值是振动信号在单位时间内的平均幅值，反映了振动信号的整体能量。

通过计算振动信号的有效值，可以了解机械设备的振动强度。

2. 峰值峰值是振动信号的最大值，表征了振动信号的峰峰值大小。

峰值是故障信号的重要特征，通过对峰值的分析，可以检测设备是否存在故障。

3. 偏度与峭度偏度和峭度是描述振动信号分布形态的统计特征。

偏度反映了振动信号分布的对称性，峭度反映了振动信号分布的尖锐程度。

通过对偏度和峭度的计算，可以判断振动信号是否存在异常状态。

三、故障诊断与机械振动信号的识别基于机械振动信号的谱分析和特征提取，可以实现对设备故障的诊断和识别。

第2章 双谱估计2.1 双谱密度函数性质·三阶累积量性质设{})(n x 是三阶零均值平稳过程，则[])()()(),(2121,3m n x m n x n x E m m C x ++= (2.1)三阶累积量具有如下对称性),(),(),(212,312,321,3m m m C m m C m m C x x x --==),(),(221,3112,3m m m C m m m C x x --=--=),(121,3m m m C x --= (2.2)[第1章累积量性质（2）表明，k 阶累积量具有!k 种对称形式。

所以3阶累积量有6种对称形式]1° 证明：),(),(121,321,3m m m C m m C x x --=∵[])()()(),(121121,3m m n x m n x n x E m m m C x -+-=-- 设i m n =-1，即i m n +=1则 原式[]),()()()(21,321m m C m i x i x m i x E x =++= 2° 证明：),(),(212,321,3m m m C m m C x x --=∵[])()()(),(212212,3m m n x m n x n x E m m m C x -+-=--令i m n =-2，即2m i n +=则 原式[]),()()()(21,312m m C m i x i x m i x E x =++=图2.1 三阶累积量的对称区·双谱定义[]∑∑∞-∞=∞-∞=+-=12)(exp ),(),(221121,321,3m m xx m m j m m CB ωωωω (2.3)存在条件 ∞∑∑ 12),(21,3m m xm m C·双谱性质1° []),(exp ),(),(2121,321,3ωωωωωωB x x j B B Φ=其中),(21,3ωωx B 幅度，),(21ωωB Φ相位，双谱通常是复数。