公平的席位分配问题建模作业

席位分配问题是一个常见的实际问题，涉及到资源的分配和管理。

为了解决这个问题，我们可以使用数学建模的方法，通过建立数学模型来分析和优化席位的分配方案。

一、问题描述假设有一个大型会议，需要分配给不同的参与者席位。

每个参与者可能有不同的资格和需求，我们需要根据一定的规则来分配席位。

具体问题包括：1. 参与者数量和席位数量2. 参与者的资格和需求3. 席位分配的规则和标准二、数学建模为了解决席位分配问题，我们可以使用以下数学模型：1. 参与者集合P：表示所有的参与者。

2. 席位集合S：表示所有的席位。

3. 资格矩阵A：表示每个参与者的资格情况，每一行表示一个参与者，每一列表示一个资格类型（例如，专业、身份等）。

4. 需求矩阵D：表示每个参与者对席位的需求情况，每一行表示一个参与者，每一列表示一个席位类型（例如，地点、时间等）。

5. 分配规则R：表示席位的分配规则和标准，如按照资格优先、按照需求优先、按照公平分配等。

根据以上描述，我们可以建立如下的数学模型：目标函数：最小化席位浪费（即席位数与参与者需求之差）约束条件：1. 资格约束：每个参与者的资格必须满足分配规则的要求。

2. 需求约束：每个参与者所需席位类型必须得到满足。

3. 数量约束：总的席位数必须不超过总席位数量。

4. 可行性约束：分配的席位必须是有效的，即不存在冲突和重复的情况。

三、求解方法根据上述数学模型，我们可以使用以下方法进行求解：1. 枚举法：逐个尝试所有可能的席位分配方案，找到满足约束条件的方案。

这种方法需要大量的计算时间和空间，但在某些情况下可能找到最优解。

2. 优化算法：使用优化算法如遗传算法、粒子群算法等，通过不断迭代找到最优解。

这种方法需要一定的编程知识和技能，但通常能够快速找到满意的解。

3. 启发式算法：使用启发式算法如模拟退火、蚁群算法等，通过不断尝试找到满意解。

这种方法相对简单易行，但可能无法找到最优解。

4. 数学软件求解：使用专门的数学软件如Matlab、Python等，通过编程求解上述数学模型。

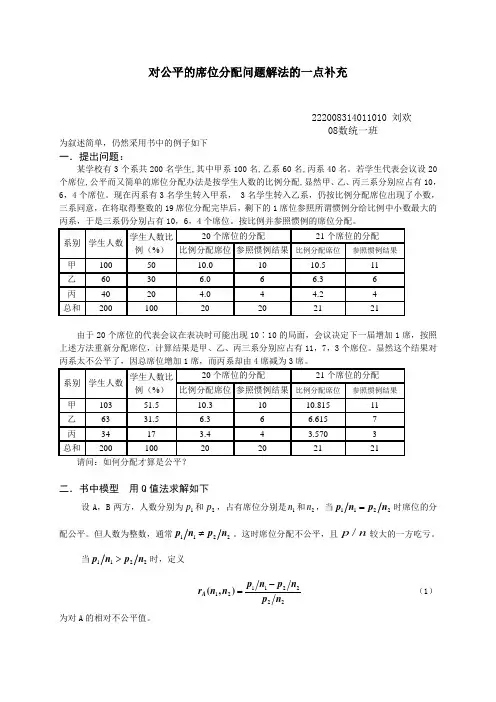
对公平的席位分配问题解法的一点补充222008314011010 刘欢08数统一班为叙述简单，仍然采用书中的例子如下一．提出问题：某学校有3个系共200名学生,其中甲系100名,乙系60名,丙系40名。

若学生代表会议设20个席位,公平而又简单的席位分配办法是按学生人数的比例分配,显然甲、乙、丙三系分别应占有10，6，4个席位。

现在丙系有3名学生转入甲系， 3名学生转入乙系，仍按比例分配席位出现了小数，三系同意，在将取得整数的19席位分配完毕后，剩下的1席位参照所谓惯例分给比例中小数最大的丙系，于是三系仍分别占有10，6，4个席位。

按比例并参照惯例的席位分配。

由于20个席位的代表会议在表决时可能出现10∶10的局面，会议决定下一届增加1席，按照上述方法重新分配席位，计算结果是甲、乙、丙三系分别应占有11，7，3个席位。

显然这个结果对丙系太不公平了，因总席位增加1席，而丙系却由4席减为3席。

请问：如何分配才算是公平？二．书中模型 用Q 值法求解如下设A ，B 两方，人数分别为1p 和2p ，占有席位分别是1n 和2n ，当1122=p n p n 时席位的分配公平。

但人数为整数，通常1122≠p n p n 。

这时席位分配不公平，且/p n 较大的一方吃亏。

当1122>p n p n 时，定义11221222-=(,)A p n p n r n n p n （1）为对A 的相对不公平值。

当1122<p n p n 时，定义22111211-=(,)B p n p n r n n p n （2）为对B 的相对不公平值。

要使分配方案尽可能公平，制定席位分配方案的原则是使12(,)A r n n 和12(,)B r n n 都尽可能小. 假设，A B 两方分别占有1n 和2n 席，利用相对不公平值A r 和B r 讨论，当总席位增加1席时，应该分配给A 还是B 。

不妨设1122>p n p n ，即对A 不公平，当再分配一个席位时，有以下三种情况：(1) 当221>+11p pn n 时，说明即使给A 增加1席，仍然对A 不公平，所以这一席显然应给A 方. (2)当221<+11p pn n 时，说明给A 增加1席后，变为对B 不公平，此时对B 的相对不公平值为 21121211-1 ++=()(,)B p n r n n p n （3）(3)当221>+11p pn n 时，这说明给B 增加1席，将对A 不公平，此时对A 的相对不公平值为12122111-1 ++=()(,)A p n r n n p n （4）因为公平分配席位的原则是使相对不公平值尽可能小，所以如果121211 +<+(,)(,)B A r n n r n n （5）则这1席给A 方，反之这1席给B 方.由(3)(4)可知，(5)等价于21222211<11++()()p p n n n n （6）不难证明上述的第(1)种情况221>+11p pn n 也与(6)式等价,于是我们的结论是当(6)式成立时,增加的1席应给A 方,反之给B 方。

数学建模论文-席位公平分配问题数学建模论文(席位公平分配问题)席位公平分配问题摘要本文讨论了席位公平分配问题以使席位分配方案达到最公平状态。

我主要根据了各系人数因素对席位获得的影响，首先定义了公平的定义及相对不公平的定义，采用了比例模型、汉丁顿模型和Q值模型制定了一个比较合理的分配方案。

首先，我根据相关资料的查阅，定义了公平的定义和不公平的定义以及不公平程度的定义和相对不公平数的定义以便来检验模型的公平性程度。

其次，我建立了一个比例模型，采用了比例相等的方法，列出一个关于所获席位与总席位数和各系人数与各系总人数的等式，进而求得所获席位数。

同时我建立了一D+Q值模型，通过汉丁顿模型和Q值模型的结合，最终得出一个比较合理的分配方案。

最后，我用相对不公平数来检验两个模型的公平性程度。

关键词:数学建模公平定义 Q值模型 d'Hondt(汉丁顿)模型1目录一、问题重述与分析: ................................... 3 1.1问题重述: ........................................ 3 1.2问题分析: ........................................ 3 二、模型假设 .......................................... 4 三、符号说明 .......................................... 4 四、模型建立: ........................................ 5 4.1公平的定义: ...................................... 5 4.2不公平程度的表示: ................................ 5 4.3相对不公平数的定义: .............................. 5 4.4模型一的建立:(比例分配模型) ...................... 6 4.5模型二的建立:(d'hondt模型和Q值模型) (6)五、模型求解 .......................................... 8 5.1模型一求解: ...................................... 8 5.2模型二的求解: .................................... 8 六、模型分析与检验 ..................................... 9 七、模型的评价: ...................................... 11 7.1、优点: ......................................... 11 7.2、缺点: ......................................... 11 7.3、改进方向: ..................................... 11 八、模型优化 ......................................... 11 九、参考文献 (12)2一、问题重述与分析:1.1问题重述:三个系学生共200名(甲系100，乙系60，丙系40)，代表会议共20席，按比例分配，三个系分别为10，6，4席。

数学建模论文（席位公平分配问题）席位公平分配问题摘要本文讨论了席位公平分配问题以使席位分配方案达到最公平状态。

我主要根据了各系人数因素对席位获得的影响，首先定义了公平的定义及相对不公平的定义，采用了比例模型、汉丁顿模型和Q值模型制定了一个比较合理的分配方案。

首先，我根据相关资料的查阅，定义了公平的定义和不公平的定义以及不公平程度的定义和相对不公平数的定义以便来检验模型的公平性程度。

其次，我建立了一个比例模型，采用了比例相等的方法，列出一个关于所获席位与总席位数和各系人数与各系总人数的等式，进而求得所获席位数。

同时我建立了一D+Q值模型，通过汉丁顿模型和Q 值模型的结合，最终得出一个比较合理的分配方案。

最后，我用相对不公平数来检验两个模型的公平性程度。

关键词：数学建模公平定义 Q值模型 d'Hondt（汉丁顿）模型目录一、问题重述与分析： (3)1.1问题重述： (3)1.2问题分析： (3)二、模型假设 (4)三、符号说明 (4)四、模型建立： (5)4.1公平的定义： (5)4.2不公平程度的表示： (5)4.3相对不公平数的定义： (5)4.4模型一的建立：（比例分配模型） (6)4.5模型二的建立：（d'hondt模型和Q值模型） (6)五、模型求解 (8)5.1模型一求解： (8)5.2模型二的求解： (8)六、模型分析与检验 (9)七、模型的评价： (11)7.1、优点： (11)7.2、缺点： (11)7.3、改进方向： (11)八、模型优化 (11)九、参考文献 (12)一、问题重述与分析：1.1问题重述：三个系学生共200名（甲系100，乙系60，丙系40），代表会议共20席，按比例分配，三个系分别为10，6，4席。

现因学生转系，三系人数为103, 63, 34, 问20席如何分配。

若增加为21席，又如何分配。

因此存在席位公平分配问题，以下针对各系自身人数对所获席位数目的影响建立相关模型，解得最优的席位公平分配方案。

公平的席位分配模型《数学模型》实验报告实验名称:公平的席位分配成绩:___________ 实验日期 : 2009 年 5 月 4 日实验报告日期: 2009 年 5 月 18 日一、实验目的制定相对公平的席位分配方案～使席位分配尽可能的公平～此为设计型实验。

解决一些实例～比如:甲系同学103名～乙系同学63名～丙系同学34名～共200名同学～有21个席位需进行分配～求方案如何时才最为公平, 二、实验内容根据席位的相对不公平度Qi,pi^2 /ni(ni+1),i=1,2……～席位应分配给Q值较大的一方～按此方法进行分配可以求出各个系所得的席位ni。

三、实验环境MATLAB6.5四、实验步骤为了实现多方的席位分配利用了多重循环的方法～程序如下: p=input('输入各系人数:');N=input('输入总席位数:');[x,y]=size(p);n=ones(1,y);while(N>sum(n))for i=1:yQ(i)=p(i)*p(i)/(n(i)*(n(i)+1));end[i,j]=max(Q);n(j)=n(j)+1;endn五、实验结果结果为n=11,6,4。

六、实验讨论、结论寻求公平分配席位方法的关键～是建立衡量公平程度的即合理又简明的数量指标～此模型提出的指标是相对不公平度～在这个前提下得到的Q值方法应该是公平的～实验结果是成功的。

七、参考资料20个席位的分配 21个席位的分配学生人数系别学生人数的比例比例分参照惯比例分参照惯,,, 配的席位例的结果配的席位例的结果甲 103 51.5 10.3 10 10.81511 乙 63 31.5 6.3 6 6.615 7 丙 34 17.0 3.4 4 3.570 3 总和 200 100.0 20.0 20 21.000 21。

【数学建模】公平席位的分配问题基础案列某展会，AB双⽅根据⼈数分配席位：衡量公平的数量指标： p1/n1=p2/n2。

此时对AB均公平。

p1/n1>p2/n2。

此时对A不公平，因为对A放来说，每个席位相对应的⼈数⽐率更⼤。

绝对不公平度定义： p1/n1-p2/n2 = 对A的绝对不公平度问题：/*情况1*/p1=150, n1=10, p1 /n1=15 p2=100, n2=10, p2 /n2=10/*情况2*/ p1=1050, n1=10, p1 /n1=105 p2=1000, n2=10, p2 /n2=100两者对A的不公平度相同，但是很明显后者对A的不公平成都已经⼤⼤降低。

相对不公平度定义：说明：由定义知对某⽅的不公平值越⼩，某⽅在席位分配中越有利，因此可以⽤使不公平值尽量⼩的分配⽅案来减少分配中的不公平使⽤不公平值的⼤⼩确定分配⽅案： 设A, B已分别有n1 , n2 席，若增加1席，问应分给A, 还是B 不妨设分配开始时 p1 /n1> p2 /n2 ，即对A不公平。

分情况讨论： 1. 2.，说明此以⼀席给A后，对B不公平，则计算对B的不公平度。

rB(n1+1,n2). 3.，说明此⼀席给B后,对A不公平,不公平值为，rA(n1,n2+1). 4.p1/n1<p2/n2+1，这种情况不可能出现。

上⾯的分配⽅法在第1和第3种情况可以确定新席位的分配，但在第2种情况时不好确定新席位的分配。

⽤不公平值的公式来决定席位的分配，对于新的席位分配，若有则应该增加给A⼀席，否则则应该增加给B⼀席。

提炼模型： ————>引⼊公式： 于是知道增加的席位分配可以由Qk的最⼤值决定，且它可以推⼴到多个组的⼀般情况。

⽤Qk的最⼤值决定席位分配的⽅法称为Q值法。

数学建模练习题一．某学校有三个系共200名学生,其中甲系100名,乙系60名,丙系40名.若学生代表会议设20各级席位,公平而又简单的席位分配方法是按学生人数的比例分配,显然甲乙丙三系分别应占有10,6,4个席位,现在丙系有6名学生转入甲乙两系,各系人数如表第二列所示,仍按比例(表中第三列)分配席位时出现了小数(表中第四列),在将取得整数的19席分配完毕后,三席同意剩下的1席参照所谓惯例分给比例中小数最大的系,于是三系分别占有10,6,4席(表中第5列)因为有20个代表会议在表决的时候可能出现10:10的局面,会议决定下一届增加一席,他们按照上述方法重新分配席位,计算结果见表6,7列,显然这个结果对丙系太不公平了.因为总席位增加一席,而丙系却由4席减为3席.按照比例并参照惯例的席位分配甲103 51.5 10.3 10 10.815 11乙63 31.5 6.3 6 6.615 7丙34 17.0 3.4 4 3.570 3总和200 100.0 20.0 20 21.000 21要解决这个问题必须舍弃所谓惯例，找到衡量公平分配席位的指标，并由此建立新的分配分配方法解答:Pī/Nī表示第ī个单位每个代表名额代表的人数采用相对标准,引入相对不公平概念.如果P1/n1>P2/n2,则说明A方是吃亏的,或说对A方不公平.对A的相对不公平度:rA(n1,n2)=(p1/n1-p2/n2)/(p2/n2)=(p1n2)/(p2n1)-1对B的相对不公平度:rB(n1,n2)=(p2n1)/(p1n2)-1情形1:P1/(n1+1)>p2/n2,表明即使A方再增加一个名额,仍然对A方不公平,所以这个名额当然给A方情形2:P1/(n1+1)<p2/n2,表明A增加一个名额后,就对B方不公平,这时B的相对不公平度为:rB(n1+1,n2)=p2(n1+1)/p1n2-1情形3:(P1/n1)>p2/(n2+1) ,表明B增加一个名额后,就对A方不公平,这时A的相对不公平度为: rA(n1,n2+1)=p1(n2+1)/p2n1-1由以上三种情形可知,若情形1发生,名额给A方.否则须考查rB(n1+1,n2)和rA(n1,n2+1)的大小关系.如果rB<rA,则名额给方,否则给B方.由于rB(n1+1,n2)<rA(n1,n2+1)等价于P2＊P2/n2(n2+1)< P1＊P1/n1(n1+1)若情形1发生,上式仍成立,记作Qi=pi＊pi/ni(ni+1)增加名额给Q值较大一方.Q甲=103＊103/10(10+1)=96.445Q乙=63＊63/6(6+1)=94.5Q丙=34＊34/4(4+1)=57.8因此名额加给甲班二，不确定环境下供应链的生产与订购决策问题不确定环境下供应链的生产与订购与订购决策问题摘要供应链管理作为一种新型企业关系管理模式在现代市场竞争中为企业生产和发展提供了一种工具,本文就 A 题给出的在不确定环境下供应链的生产和订购决策问题进行研究,展开讨论,分析和建立数学模型,利用数学软件进行求解. 对于问题一:只考虑包含一个生产商和一个销售商的供应链,在假设商品的最终需求量是确定的,而生产商生产商品量是不确定的情况下采用线性规划的方法建立数学模型,分别建立生产商和销售商获得利润的两个方程式,针对两个方程中的一些变量进行限制,当生产商和销售商的利润同时达到最大值时就是该供应链的最优解,最后利用 lingo 软件进行编程和求解. 对于问题二:在问题一的供应链的基础上,增加了一个条件那就是我们商品的市场需求量也是随机的,并且有一个商品市场需求量的期望值=400,需求量的波动区间是[0.8,1.2], 利用正态分布中的 3 原则,求解出 ,再利用正态分布的密度公式Ρ √2 1 , ∞ ∞ 列出一个相关式求解出求解出销售商的最优订购量 Oi 再利用线性规划的方法将所求的 Oi 做为一个已知数列解一个生产商所获利润的方程,并且加入相应的限制条件就可求出生产商最优计划产量的最优解. 对于问题三:考虑在实际生产中,大多数供应链具有两级不确定性,即原产品生产的不确定性和产成品生产的不确定性;总体再利用线性规划的相关性列出两个线性方程,以及对其加入相应的限制条件,求解出供应链中二级生产商的最优订购量和一级生产商的最优计划产量. 关键词: 关键词:供应链线性规划正态分布最优订购量最优计划产量 1. 问题对于第一问和第二问,只考虑包含一个生产商和一个销售商的供应链,即销售商向生产商订购商品,生产商将商品按批发价格批发给销售商,销售商将商品按销售价格销售给最终顾客.其中相关已知条件有如下表所示: 生产成本/个生产商销售商 20 库存成本/个 5 5 缺货赔偿金/个出售价格/个 15 25 40 60 (1)若假设商品的最终需求量是确定的,即商品市场需求量为 400.而生产商生产商品量是不确定的,即由于受到各种随机因素的影响,商品实际产量可能不等于计划产量,呈随机波动,若生产商计划生产量为 Q,则商品生产量的波动区间为[0.85,1.15],即产品实际产量的区间为[0.85Q,1.15Q].. 建立数学模型, 确定销售商的最优订购量和生产商的最优计划产量. 根据建立的数学模型,求解供应链中销售商的最优订购量和生产商的最优计划产量. (2)在问题(1)的供应链中,如果商品的市场需求量也是随机的,商品市场需求量的期望为400,市场需求量的波动区间为[0.8,1.2],即实际市场需求量的区间为[320,480].请建立数学模型,确定销售商的最优订购量和生产商的最优计划产量.根据建立的数学模型,求解供应链中销售商的最优订购量和生产商的最优计划产量. 对于第三问,考虑在实际上,大多数供应链具有两级生产不确定性,即原产品生产的不确定性和产成品生产的不确定性,一级生产商生产原产品(或原材料) ,二级生产商向一级生 5 产商订购原产品(或原材料) ,并通过加工原产品(或原材料)生产产成品,进而销售给最终顾客,两级生产均具有不确定性.相关的已知条件如下表所示: 生产成本/个库存成本/个缺货赔偿/个加工成本/个售价/个一级生产商二级生产商 20 5 7 15 30 10 40 95 (3)若假设产成品的市场需求量是确定的,即产成品市场需求量为 280.原产品生产量的波动区间为[0.85,1.15],产成品生产量的波动区间为[0.9,1.1].请建立数学模型,研究在两级生产不确定的供应链中,二级生产商(产成品生产商)的最优订购量和一级生产商(原材料或原产品生产商)的最优计划产量.根据建立的数学模型,求解供应链中二级生产商的最优订购量和一级生产商的最优计划产量. 2 符号说明销售商的利润生产商的利润一级生产商利润二级生产商利润销售商订购量二级生产商的订购量商品生产量的波动区间和原产品生产量的波动区间系数产成品生产量的波动区间系数实际市场需求量波动系数生产商和一级生产商的最优计划生产量商品市场需求量的期望值 1. 生产商的计划生产量始终大于订购量; 2. 市场的最终需求是确定的;3. 商品生产量波动是连续的; 3 模型假设4. 市场需求量波动是连续的且服从正态分布;5. 原材料生产量的波动是连续的. 6 4,问题分析这是一个优化问题,要决策的是生产商的最优计划量和销售商的最优订购量,即所谓的优化组合,要达到的目标有二, .一般来说这两个目标是矛盾的,销售商订购的越多(在生产商的能力范围之内) ,生产商的净收益越大,但销售商的市场需求量是有约束的,销售商卖不出去,就要储存需要库存成本,那销售商的净收益就会很小.所以需要更多的约束条件使这两个目标同时达到最优的即所谓的最优决策,我们追求的只能是,在确定的订购量下生产商的净收益最大的决策,和在确定的生产量下销售商净收益最大的决策,使生产商的计划生产量和销售商的订购量按一定比例组合最优的决策.这就是说在不同的约束条件下,只要建模合理,答案可以是多种. 建立优化问题的模型最主要的是用数学符号和式子表述决策变量,构造目标函数和确定约束条件.对于本题决策变量是明确的,即最优计划量,销售商的最优订购量商品,生产量的波动值和市场实际需求量的波动值(题中第一问的该值为一) ,目标函数之一是销售商的总收益最大,目标函数之二是生产商的总收益最大.而生产商的总收益用他的实际生产量和销售商的订购量衡量,销售商的总收益用他的订购量和市场的实际需求量衡量. 5,模型建立 5.1 问题一,二供应链的相关关系图如下所示: 计划生产量实际生产量订购量市场需求量销售商销售销售产品批发生产商生产产品成本批发价产品库存成本库存成本缺货赔偿金缺货赔偿金销售单价 7 5.2 问题一模型的建立对于问题 1 模型的建立,讨论如何调整销售商的订购量和生产商计划生产量使生产商和订购商的利润最大. 根据前面的模型假设,从生产商的角度考虑,由于单位商批发缺货成本太大,所以不予考虑缺货状态下销售商利润和生产商的利润.计划生产量是假想情况下在规定的时间所能生产的产品量,但总有突发事件发生导致生产商的计划生产量与实际生产量有出入,生产商为了保证自己的利润最大即花费不至过大,一定不能缺货,因为缺货一个所损失的赔偿金抵上多生产三个产品在储存上的花费.而不能缺货,生产商的计划产量就要始终大于订购商的订购量.而从销售商的角度考虑,订购量与上述生产商一致,不能缺货,因为缺货一个所损失的赔偿金抵上多订购五个产品在储存上的花费,而在成本方面,现在卖不出去以后搞促销一样可以卖出去.具体分析如下: 1)当 Q>400,既订购量大于市场需求量,所以销售商和订购商的利润分别为: max=60*400-40* max=40* -20* -5*( *Q-5*( -400); *Q) (1) (2) 当 Q<400,即订购量小于市场需求量,所以销售商和订购商的利润分别为: max=60*400-40* -25*(400max=40* )(3) -20* *Q-15*( *Q) (4) 针对上述描述分析中的各种范围讨论,我们采用的是线性规划方法,先利用供应链中各种数据存在的关系,列出生产商和销售商利润求值关系式,如下所示: 1 2 60 400 40 40 20 5 5 400,0 25 ,0 15 400 ,0 ,0 (5) (6) 当供应链中生产商的利润 Pj 与销售商的利润 Pi 在应链的限制条件中同时达到最大值时, 8 我们就可以利用数学软件编程求解出我们的销售商的最优订购量 Oi 和生产商的最优计划产量Q .5.3 问题二模型的建立对于问题 2 模型的建立,在问题一的基础上,商品市场需求量变为随机的,讨论如何调整销售商的订购量和生产商计划生产量使生产商和订购商的利润最大.我们首先知道了商品市场需求量的期望值为 400,根据条件已知期望,属于概率与数理统计范围,又根据前面模型假设知道了销售商的实际订购量符合正态分布根据正态分布中 3 原则即: 设Χ~Ν , ,则Ρ |Χ | σΦΦ0.6826, 0.9545, 0.9973, 1; 2; 3. 从上式中可以看出:尽管正态变量的取值范围是( ∞,。

数学建模论文单位：湖南信息职业技术学院系别: 信息工程系班级: 信息0903作者: 贺际嵘公平的席位分配问题[摘要]我们用公平席位分配模型,解决了10人委员会人员组成问题并保证对A.B.C的相对都公平.首先,我们用人们常用的惯例分配席位的方法来分配10个席位得出结果如表1-1；再假定情况1,也用惯例分配席位的方法来分配得出结果如表2-2；由以上两步的结果可以判定此种按照人数比例分配的惯例分配方法在这里应用分配的结果是不公平的,导致总席位数N增加一个,A的席位数反而减少了一个；此后,我们在寻找一个更为公平的分配方案,经过对问题的深入了解,逐步分析并结合各种情况的共同性建立我们日常寻求的更为公平的分配方案—Q值法；最后,我们通过Q值法求的本问题的最佳分配结果,也进一步,把这一以Q值法为为方法的公平席位分配模型推广到我们的日常生活中所遇到的席位分配问题.通过公平席位分配模型对席位的分配,不难检验出惯例分配席位的方法是不公平的,总席位数为N=10 的公平分配结果是: A是n1=2, B是n2=3,C是 n3=5.[关键字]公平分配；Q值法；模型．1 问题重述我们日常生活之中经常会面对席位分配的问题,如某学校共1000学生,235人住在A楼,333人住在B楼,432住在C楼. 学生要组织一个10人委员会,我们可以试用惯例分配方法和Q值方法分配各楼的委员数,并比较结果,试得出更为公平的分配方案及结果.事先我们可以对问题进行假设与符号定义；然后进行我们的问题分析,先用惯例分配分配席位的方法分析：①可以先人们常用的惯例分配席位的方法来分析公平分配10个席位并得出结果；②也可以再假定情况1,也用惯例分配席位的方法来分析并得出结果；两种结果进行分析以初步得出惯例分配席位的方案是不公平的,并思考怎样才能得出更为公平的分配方案；然后,我们把模型建立方面的分析及其模型建立放在模型建立里面再分析.2 问题的假设与符号定义1.1问题的假设:1.席位是以整数计量的,并且为有限个,设为N个；2.每个单位有有限个人,席位是按各集体的人员多少来分配的；3．每个单位的每个人都具有相同的选举权利；4．每个单位至少应该分配到一个名额,如果某个单位,一个名额也不应该分到的话,则应将其剔除在分配之外；5．在名额分配的过程中,分配是稳定的,不受任何其他因素所干扰.1.2符号的定义：n---－表示某单位的席位数（n1、n2、n3分别表示A、B、C的席位数）；p----表示某单位的人数（p1、p2、p3分别表示A、B、C的人数）；q-------表示总席位数；N-------表示人数.Q-------表示某单位的Ｑ值.3 问题的分析通常人们都是按照人数比例来进行分配的.当比例中有小数时,人们又按照惯例将多余的席位分给比例中小数最大者.我们能得出以下结论：*n/公式：Npq3.1 惯例分配总席位数为N=10的结果：我们用惯例分配席位的方法分配,结果为n1 =3、n2=3、n3=4,分配过程及结果如表2-1所示：楼层人数p 所占比例(q/N) 分配方案席位(n)A 1 235 235/1000 (235/1000)*10=2.35 3B 2 333 333/1000 (333/1000)*10=3.33 3C 3 432 432/1000 (432/1000)*10=4.32 4表2－１惯例分配总席位数为N=10的分配过程及结果.3.2 假定情况一: 若增加为11席,分配有何变化?我们也运用惯例分配席位的方法分配,结果为n1 =2、n2=3、n3=5,分配过程及结果如表2-2所示：楼层人数p 所占比例（q/N）分配方案席位（n）A 1 235 235/1000 (235/1000)*11=2.59 2B 2 333 333/1000 (333/1000)*11=3.66 4C 3 432 432/1000 (432/1000)*11=4.75 5表2－2 惯例分配总席位数为N=11的分配过程及结果.现象一:总席位增加1席, A 减少１席位．（不公平！）显然,存在不公平现象,能否给出更公平的分配席位的方案？4 模型建立目标:建立公平的席位分配方案.4.1 引出绝对不公平值并给出相对不公平值:设A,B 两方人数分别为21,p p ；分别占有 1n 和2n 个席位,则两方每个席位所代表的人数分别为11n p 和 22n p. 我们称 2211n p n p -为.例：10,100,1202121====n n p p则22211=-n p n p ； 又 10,1000,10202121====n n p p 则22211=-n p n p 由上例可知,用绝对不公平程度作为衡量不公平的标准,并不合理,下面我们给出相对不公平值.①若 2211n p n p > 则称 11221222211-=-n p n p n p n p n p 为对A 的相对不公平值, 记为 ),(21n n r A ；②若 2211n p n p < 则称 12112111122-=-n p n p n p n p n p 为对B 的相对不公平值 ,记为 ),(21n n r B .4.2给出相对公平的席位分配方案:如果，A B 两方分别占有1n 和2n 席,利用相对不公平值A r 和B r 讨论,当总席位增加1席时,应该分配给A 还是B.不妨设1122>p n p n ,即对A 不公平,当再分配一个席位时,有以下三种情况：I .当221>+11p pn n 时,这说明即使给A 增加1席,仍然对A 不公平,所以这一席显然应给A 方.II.当221<+11p pn n 时,这说明给A 增加1席,变为对B 不公平,此时对B 的相对不公平值为:21121211-1 ++=()(,)B p n r n n p n （3）III.当221>+11p pn n 时,这说明给B 增加1席,将对A 不公平,此时对A 的相对不公平值为:12122111-1 ++=()(,)A p n r n n p n （4）因为公平分配席位的原则是使相对不公平值尽可能小,所以如果121211 +<+(,)(,)B A r n n r n n （5）则这1席给A 方,反之这1席给B 方.由(3)(4)可知,(5)等价于21222211<11++()()p p n n n n （6）不难证明上述的第I 种情况221>+11p pn n 也与(6)式等价,于是我们的结论是当(6)式成立时,增加的1席应给A 方,反之给B 方.若记:2, =1,21=+()i i i i p Q i n n则增加的1席给Q 值大的一方.4.3模型内部推广:上述方法可以推广到有m 方分配席位的情况.设第i 方人数为i p ,已占有i n 个席位.当总席位增加1席时,计算:2, =1,21=+()i i i i p Q i m n n ，，则增加的1席应分配给Q 值大的一方.这种席位分配的方法称为Q 值法.5 模型求解5.1下面用Q 值法讨论A,B,C 层分配11个席位的问题：先按照比例将整数部分的9席分配完毕n 1=2, n 2=3, n 3=4,.再用Q 值法分配第10席和第11席.分配第10席,计算得:9204.173*223512==Q ；9240.754*333322==Q ；9331.205*443232==Q ； 3Q 最大,于是这1席应分给C 层.即: n 1=2, n 2=3, n 3=5. 分配第11席,计算得:9204.173*223512==Q ；9240.754*333322==Q ； 80.22066*543232==Q ,Q 2最大,于是这1席应B 层. 即: n 1=2, n 2=4, n 3=5.5.2现象分析及结果：根据Q 值分配结果与假定情况一的现象,易得出:惯例分配总席位为10时,分配不公平,以至得出总席位数N 增加一个,A 的席位数反而减少了一个的错误结论.原因在于分配时,应给C 的1个席位反而给了B ；10人委员会组成为:Ａ.Ｂ.Ｃ的席位数分别 2、3、5.6 模型评价●我们巧用绝对值,避免了分两种情况.从而简化了运算. ●改进后的Q 值法席位分配方案应用性推广,分配更公平.7 参考文献[1]李志林等,数学建模及典型案例分析,北京：化学工业出版社,2006.。

公平分配席位数学建模
公平分配席位数学建模是指基于数学模型，通过分析选民分布、政党得票率等因素，确定选举中各政党应该获得的议席数，从而实现选举结果的公正和公平。

在公平分配席位数学建模中，主要运用了几种方法，包括杜哈美—贝勒多尼定理、圆整法、最大余数法、谢泼德方法等。

这些方法都能够根据选民分布和政党得票率等因素，计算出每个政党应该获得的议席数，并且保证在分配过程中不会出现偏差和不公平现象。

公平分配席位数学建模不仅在政治选举中有着广泛的应用，还可以用于企业、学校等组织内部的决策和分配问题。

通过数学建模，可以实现公正合理的决策和资源分配，提高组织的效率和公信力。

总之，公平分配席位数学建模是一种重要的数学工具，可以帮助我们实现公正公平的选举和决策，具有广泛的应用前景和社会价值。

- 1 -。

公平席位的分配模型1 问题提出某高校有200名学生，其中1系有100名学生，2系有60名学生，3系有40名学生，现在要成立一个20席位的委员会， 按照要求解决下述问题：问题一：问应该如何分配，使每个学生得到席位的可能性相同？ 问题二：若现在学生中存在转系的情况，1系现有103名学生，2系现有63名学生，3系现有34名学生，那么如何分配才能使其公平？ 问题三：若现在增加一个席位，即21席，那又该如何分配？ 2 合理假设与变量说明 2.1 合理假设2.1.1 模型的公平定义是相同的。

2.1.2 模型所要求的公平是绝对公平。

2.1.3 模型不考虑各系自身的要求。

2.1.4 分配到各系的名额数目均为整数。

2.2 变量说明设 P 为总人数，i P 为各方人数， （,iP P N +∈，1,2,,i n =⋅⋅⋅，n N +∈），N为总席数，i N 为各方的分配席数，（,1,2,,iNN i n+∈=⋅⋅⋅，n N +∈）且1n i i N N=∑=，1nii P P =∑=3 问题分析通常分配结果的公平与否以每个代表席位所代表的人数相等或接近来衡量。

目前沿用的惯例分配方法为按比例分配方法，即：学生代表席位分配数=学生总人数比例 总席位如果按照上述公式参与分配的一些学生代表的席位分配数出现小数，则先按席位分配数的整数分配席位，余下席位按所有参与分配学生中小数部分最大的优先分配。

得到最初学生人数及学生代表席位如下表：表1：按比例的席位分配表考虑学生转系以及增加一个席位等的情况，各系学生人数及学生代表席位变为：表2：按照比例并参照惯例的席位分配由上表（参考文献[1]）可以看出，20系应该1系10席，2系6席，3系4席这样分配，21席的分配结果由上表可知，这个结果出现增加一席后，3系比增加席位前少一席的情况，这就使人觉得席位分配明显不公平。

要怎样才能公平呢，这时需建立数学模型来解决。

4 模型建立 4.1 Q 值分配法模型设A 、B 两方的人数分别为1P ，2P ，占有的席位数分别是1N 和2N ，这两方每个席位代表的人数分别是11P N 和22P N 。

公平席位分配问题数学建模数学建模,公平席位问题所在系别:地球科学与资源系专业班级:10级土管6班姓名:刘强1一、摘要本文就是席位分配公平与否的问题。

需要联系生活想象。

它就是在达到所有系最公平的条件下寻求最好的方法，通过对各个合理的计算和研究，总结找出最佳方案。

首先用比例分配法求出本题的答案，然而考虑到实际的多重因素下，在假设一组数据进行检验，然后便发现了问题，即:很多时候根本没有公平的分配方法，我需要另寻其他方法。

找到了以下关于分配的方法:Hamilton (哈密顿)方法、d’Hondt 接着我(汉丁顿)方法、Q值方法、d’Hondt(汉丁顿)方法+Q值法。

将对这些方法进行逐一分析与检验，使得得出一套最佳的合理方案。

即:使得各系席位分配最公平。

关键词:公平分配、最佳方案、最公平二、问题的重述某校有200名学生，甲系100名，乙系60名，丙系40名，若学生代表会议设20个席位，问三系各有多少个席位,三、问题的提出与分析分配问题是日常生活中经常遇到的问题，它涉及到如何将有限的人力或其他资源以“完整的部分”分配到下属部门或各项不同任务中。

它涉及的内容十分广泛。

此题一个自然的问题是如何分配席位名额才是公平的呢,反映公平分配的数量指标可用每席位代表的人数来衡量。

即:mi / xi当各系每席位代表的人数相等时，则就是最公平的分配方法。

此题公平的席位分配办法是按学生人数的比例分配，显然甲、乙、丙三系分别占有10、6、4个席位。

但是比例分配在实际生活中的应用并不广泛，原因是当所得结果并非整数时，就难以解决了。

此时就需要另寻其他方法了。

Hamilton (哈密顿)方法、d’Hondt(汉丁顿)方法、Q值方法均是求如何分配所总结的方法。

那么什么方法使得能够更大的获得公平呢,四、符号的约定• N 表示总席位数• s 表示系数• ni(i=1.2.3……s) 表示第i个系• mi(i=1.2.3……s) 表示各系中的人数• xi(i=1.2.3……s) 表示各系所获得的席位数?、采用比例分配法xi=(mi/N)*总席数20个席位的分配结果如下表人数系别ni 所占比例分配方案席位数xi mi甲 100 100/200 (50/100)*20=10 102乙 60 60/200 (30/100)*20=6 6丙 40 40/200 (20/100)*20=4 4• 但是我发现实际生活中结果是整数的情况少之又少，• 所以对此我们假设下面这种情况作为参考。

公平的席位分配的实验
一、 实验概述
实验目的
1、 理解数学建模结果的不唯一性，渐近性与可转移性。

了解数学
建模的基本思路，通过一建模实例，掌握建模的基本方法。

2、 会对模型在问题分析的基础上提出合理的假设，会创造性应用
数学知识进行简单的建模活动。

3、 学会用数学的方法解决一些实际的问题
4、 学习把现实问题抽象化，建立数学模型
5、 建模坚持没有最好，只有更好
实验原理
运用初等数学的方法来构造和求解模型，通过简单的数学方法可以解决一些实际问题。

Q 值法; 知道增加的席位分配可以由 的最大值决定，且它可以推广到
多个组的一般情况。

实验环境
VC++6.0编程系统
WINDOWS XP 操作系统
二、 实验内容
整个的实验过程是一个求公平分配席位的过程
问题：
s i n n p Q i i i i ,2,1,)
1(2 =+=i Q
学校共有1000名学生，235人住在A楼，333人住在B楼，432人住在C楼．学生们要组成一个10人委员会，使用Q值方法及哈密顿方法给出分配方案．如果委员会为15人，分配方案是什么?
此次试验采用Q值法;哈密顿模型来解决问题
1）建立数学模型
即用数学语言来描述最优化问题。

模型中的数学关系式反映了最优化问题所要达到的目标和各种约束条件
2）数学求解
数学模型建好后，选择合理的最优化方法进行求解
三、实验过程
四、实验结论
五、实验小结
六、几点要求：
1、要按建模的完整过程来建立模型。

2、要对模型进行必要的分析和说明，以论文的行式写作，杜绝只写出几个数学公式。

公平分配席位是一种数学建模问题，通常涉及到在一个组织或机构内，如何公平地分配有限的席位或资源给不同的成员或利益相关者。

该问题可通过以下步骤建立数学模型：
1.定义问题：明确参与者、资源和目标，确定席位数量和分配规则。

2.建立评价指标：根据目标和分配规则，建立评价指标来衡量分配方案的公平性和效
率性。

3.确定算法：选择合适的算法来进行席位分配，例如最大剩余法、顺序分配法、随机
分配法等。

4.模型求解：通过计算机程序或手工计算，进行模型求解，得出最优分配方案。

5.结果分析：对比各个方案的评价指标，选择最优方案并进行结果分析，验证模型的
可靠性和有效性。

公平分配席位模型可以应用于政治、教育、医疗、社会保障等领域，如选举、大学招生、医疗资源分配、社会福利等。