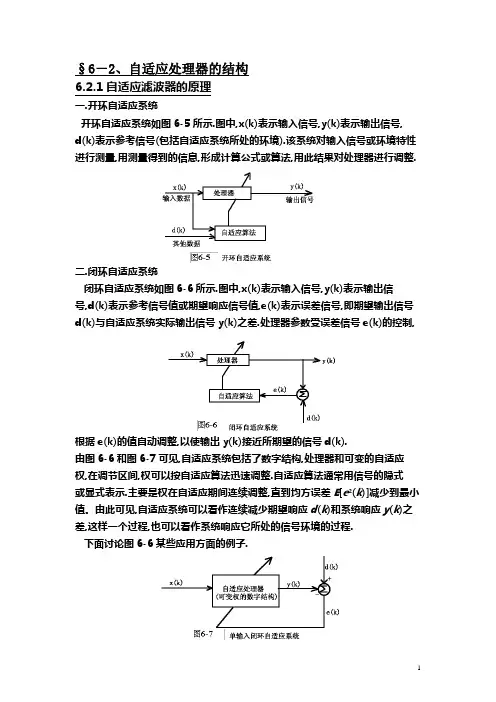
§6－2、自适应处理器的结构6.2.1自适应滤波器的原理一.开环自适应系统开环自适应系统如图6-5所示.图中,x(k)表示输入信号,y(k)表示输出信号,d(k)表示参考信号(包括自适应系统所处的环境).该系统对输入信号或环境特性进行测量,用测量得到的信息,形成计算公式或算法,用此结果对处理器进行调整.二.闭环自适应系统闭环自适应系统如图6-6所示.图中,x(k)表示输入信号,y(k)表示输出信号,d(k)表示参考信号值或期望响应信号值,e(k)表示误差信号,即期望输出信号d(k)与自适应系统实际输出信号y(k)之差.处理器参数受误差信号e(k)的控制,根据e(k)的值自动调整,以使输出y(k)接近所期望的信号d(k).由图6-6和图6-7可见,自适应系统包括了数字结构,处理器和可变的自适应权,在调节区间,权可以按自适应算法迅速调整.自适应算法通常用信号的隐式或显式表示.主要是权在自适应期间连续调整,直到均方误差E[e²(k)]减少到最小值。
由此可见,自适应系统可以看作连续减少期望响应d(k)和系统响应y(k)之差,这样一个过程,也可以看作系统响应它所处的信号环境的过程.下面讨论图6-6某些应用方面的例子.(1)自适应预测器(adaptive prediction):自适应预测器如图6-8所示.图6-8(a)为简化的不可实现的情况,自适应处理器趋向最小的E[e²(k)],因此,使得它的输出近似它的输入的未来值s(k+Δ).因为后者,在实时处理中是不可能的.图6-8(b)为可实现形式,其应用与图6-8(a)等价,而估值s^(k+Δ)用从动处理器产生.这种自适应预测器用于语音编码,谱估计,事件检测,线性增强,信号白化和其它应用领域.注意:基本的闭环自适应图6-7就置于预测图6-8当中.(2)自适应模拟(adaptive modeling):自适应模拟如图6-9所示.前向模拟如图6-9(a)所示.在前向模拟中,自适应处理器调整它的权,产生响应y(k),在最小均方意义上,尽可能与被控对象响应d(k)接近.若激励s(k)频率容量是鲁棒的,又若内部被控对象的噪声n(k)是很小的,那么,自适应处理器将变成适应未知系统的一个好的模拟.前向模拟在生物,社会,经济科学,自适应控制,数字滤波器设计,相关性估计和地球物理等方面有着广泛的应用.图6－9自适应模拟(a)前向模拟，(b)逆模拟逆模拟如图6-9(b)所示.自适应处理器调整它的权,变成被控对象的逆,即改变被控对象的输出x(k),回到输入的延迟型式s(k-Δ).延迟通常包括通过被控对象和自适应处理器的传播延迟,并假定两者为因果系统.与前向模拟类似,若s(k)是谱鲁棒的,并若n(k)是小的.自适应处理器就适应变成未知系统的精确的模型.逆模拟在自适应控制,语音分析,信道均衡,重叠合法(deconvolution),数字滤波器设计和另外的应用方面得到运用.再次注意:图6-7所示的基本的闭环自适应系统就置于图6-9(a)和图6-9(b)中.(3)自适应干扰对消(adaptive interference cancelling ):自适应干扰对消如图6-10所示.这是广泛应用的一种简单结构.假若期望响应d(k)为信号附加噪声,即s(k)+n(k),自适应处理器的输入x(k)为与n(k)相关的另外的噪声n′(k).当s(k)和n(k)是不相关的,自适应处理器由y(k)=nˆ(k),并逼近n(k),使E[e²(k)]趋向最小.因此,使e(k)逼近s(k).结果降低了在e(k)中的噪声.这里再次强调图6-7置于图6-10中.(4)自适应阵处理(adaptive array processing):自适应阵处理如图6-11所示.阵处理系统本身就是一个多输入干扰对消典型,比较图6-10和图6-11就可以看出.如同普通的波束,控制延迟,用来在观测的方向形成波束产生峰阵增益.于是,噪声目标信号s(k)+n(k)通过固定的滤波器获得,如图6-11所示.噪声估值n^(k)通过多输入处理器,用它来对消n(k),这恰如图6-10所示.图6-11中仍然使用了图6-7的基本结构.6.2.2 非递归自适应滤波器非递归自适应滤波器又称自适应线性组合器(adaptive linear combiner). 其一般形式如图6-12所示.图中,由x0(k),x1(k),…x n-1(k)组成信号向量,与之对应的为一组可调权,w0,w1,…w n-1以及求和单元∑和它的单输出信号y.调整权的方法称为自适应算法.因为是线性的,因此,对一组固定权值w0,w1,…w n-1 ,输出y是输入分量 x0(k),x1(k),…x n-1(k)的线性组合.当然,当这些权处在调整过程中时,它也是输入分量的函数,因而非递归自适 应滤波器的输出不再是输入的线性函数,它的运算就成为非线性的.本章主要讨论线性自适应系统,一般分两种情况讨论:一.单输入系统输入x 0(k),x 1(k),…x n-1(k)是由同一信号源的n 个样本序列.其输入的数学表达式为:式中,X(k)为一列向量,T 表示转置,k 为时间指标.其输出为这种滤波器的结构如图6-13所示.这种自适应处理器由非递归自适应滤波器和单位延迟单元组成.这种结构通常也称为自适应横向滤波器.这也是构成自适应系统的一种基本结构.二.多输入系统多输入系统的结构图如图6-14所示.输入向量可以认为有几个不同信号源瞬 时到达接收机,变成接收信号.相当于每一条线上连接一个独立的自适应天线(或自适应声源检测装置等).滤波器输入的表达式为式中X(k)为列向量. 滤波器的权向量为 )266...()]()...()([)(110-=-T n k x k x k x k X )276...()()()(10-=∑-=n i i i k x k w k y )286...()]()...()([)(110-=-Tn k x k x k x k X )296...()]()...()([)(110-=-T n k w k w k w kW滤波器的输出为式(6-27)和式(6-30)用向量表示,则式中 6.2.3.具有期望响应和误差信号的非递归自适应滤波器及性能函数 具有期望响应和误差信号的非递归滤波器如图6-15所示.图中,期望响应为 d(k),误差信号为e(k).当时间指标为k 时,其误差信号为将式(6-31)代入式(6-32),为了简洁,对权向量W 不加时间指标,则由式(6-33)可得瞬时平方误差,即 若e(k),d(k)和X(k)为平稳随机序列,X(k)和d(k)是不相关的,则对 )(2k e取数学期望,则若)]()([k X k X E R T = ,则)306()...()()(10-=∑-=n i i i k x k w k y )316)...(()()()()(-==k X k W k W k X k y TT ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=--)(...)()()(,)(...)()()(110110k w k w k w k W k x k x k x k X n n )326)...(()()(--=k y k d k e )336)...(()()()()(--=-=k X W k d W k X k d k e TT )346()()(2)()()()(22--+=W k X k d W k X k X W k d k e T T T )356...()]()([2)()]()([)]([)]([22--+=W k X k d E k W k X k X E W k d E k e E T TT（6－36） 式(6-36)表示的矩阵称为输入相关矩阵,主对角线是输入分量的均方值,交叉 项是输入分量之间的互相关值. 若P =E[d(k)X(k)],则 式(6-37)为期望响应与输入分量之间的一组相关值.当X(k)和d(k)为平稳时, P 和P 的元素都是固定的二阶统计量.由推导过程可知,式(6-36)和式(6-37) 对单输入形式也适用.若均方误差用ξ表示,则式(6-35)可表示为当输入分量与期望分量是平稳随机过程时,式(6-38)展开式中,W 的元素仅以一 次或二次幂出现,均方误差E[e ²(k)]是权向量W 分量的二次函数.典型的二维均方误差函数如图6-16所示.式(6-38)这是一个上凹的超抛物 面,即一个碗状二次型误差函数或性能表面是具有唯一最小值的函数.如果调节 权函数使均方误差为最小,就相当于沿抛物形曲面下降找到最小值,即让权向量 去搜索性能表面最小值.最常用的方法是梯度法.图6－16 均方误差表面为最小的位置和它对于Wopt 和ξmin 的关系曲线 换句话说,由式(6-38)看出,均方误差是滤波器系数(权)W 的函数,若式右边 W 的任何分量变化,那么,均方误差的计算值也跟着改变.因为假定W 在n 维W 平面取值是连续的.与W 有关的均方误差值在n+1维空间是连续的.对n=2,在三维⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==------)(...)()()()()()(...............)()(...)()()()()()()(...)()()()()()]()([212111011121210110201020k x k x k x k x k x k x k x k x k x k x k x k x k x k x k x k x k x k x k x k x k x k X k X E R n n n n n n T T 1-n 10(k)]x (k)...d(k)d(k)x (k)E[d(k)x =P 38)-W...(6P 2-RW W +(k)]E[d =(k)]E[e =T T 22ξ空间相应的误差"表面",通常称为均方误差表面(mean square error surface) ,或称为二次型性能表面(quadratic performance surface).图6-16中的特殊符号, 下面几节将要讨论.这里只是定性地描述均方误差表面.高ξ相应于固定滤波器 权W 的滤波信号x(k)的物理位置.若滤波器权集(w 0, w 1)=(w 0opt, w 1opt ), 则为最小均方误差 ξmin .6.2.4 梯度法(gradient methods)梯度法是一种权向量搜索性能表面最小值的自适应方法.用 ▽表示均方误差性能表面的梯度,可由式(6-38)对W 求导得到,即则式中,R 由式(6-36)给出,P 由式(6-37)给出. 令式(6-40)等于零,即可求到最佳权向量W op t , 即设 由于R 是非奇异矩阵,则 式(6-42)正是矩阵形式的维纳-霍夫方程.将式(6-42)代入式(6-38),得到 最小均方误差,即由式(6-36),则则式(6-43)可写成式(6-38)表示的均方误差ξ可以表示成二次型函数的形式,即)396]...(...[110-==∇-n w w w W∂∂ξ∂∂ξ∂∂ξ∂∂ξ )406...(22--=∇P W R )416...(022-=-=∇P W R opt )426...(1-=-P R W opt opt T opt T opt W P W R W k d E 2)]([2min -+=ξ)436...(2)()()]([1112--+=---P R P P R R P R k d E T T )446...()( 11-==--R R R R T T )456...()]([)]([212min --=-=-opt T T W P k d E P R P k d E ξ)()(minopt T opt W W R W W --+=ξξ式中,各项都为标量,故等于它的转置,因而最后两项是相等的,并将式(6-45)代入m in ξ,则 将式(6-42)代入式(6-47),则这就证明了式(6-38)和式(6-48)完全相等.二次型函数还可以表示成更简洁的形式,设 式中,V 表示权向量对维纳最优向量的偏差.式(6-46)可以写成将式(6-47)对V 求导,得到均方误差 ξ 对V 的梯度,则由于W 和V 仅差一常数.所以,式(6-51)和式(6-40)给出的梯度完全相同,则由此可见,式(6-51)是梯度的另一种表示形式.6.2.5.误差信号与输入信号正交当W=W op t 时,误差信号与输入信号向量正交.由式(6-33),有 )466...(min ---++=W R W W R W W R W W R W T opt opt T T opt T opt ξ)476...(2)]([2--++-=opt T T opt T opt opt W R W W R W W R W W P k d E ξP R R W W R W P R R R P P R P k d E T T T T 111122)]([-----++-=ξ)486...(2)]([2)]([22--+=-+=W P W R W k d E P W W R W k d E T T T T )496...(],...,[110-=-=-T n opt v v v W W V )506...(m in -+=V R V T ξξ)516...(2]...[110-==-V R v v v Vn ∂∂ξ∂∂ξ∂∂ξ∂∂ξ)526)...((22--====∇P W R V R VW ∂∂ξ∂∂ξ)536...()()()(--=W k X k d k e T将上式两边乘以X(k),由于式中每一项都为标量,X(k)左乘和右乘等价,则对上式两边取期望,则令W=W op t 时, 则式(6-56)表示的结果与维纳滤波理论的结果相同，即前面所讲的正交原理，线性变换为最小均方误差估计，当且仅当误差与其正交。
