下载文档原格式
合肥八中2014年第三次适应性考试数学(理)参考答案选择题（5分×10＝50分）1．【答案】：B【解析】：1z i =--，22z i = 2．【答案】：D【解析】：2{|1}{|11}A x x x x x =>=><-或，2{|log 0}{|1}B x x x x =>=> 3．【答案】：A【解析】：直线l 1：ax ＋2y －1＝0与直线l 2：x ＋(a ＋1)y ＋4＝0平行的充要条件是2a =-或1 4．【答案】：C 5．【答案】：A【解析】：sin sin(2)sin[2()]6y x y x y x π=→=→=+6．【答案】：C【解析】：21222(l o g )(l o g )2(2)(l og )(2)2l o g 2f a f a f f af a +≤⇒≤⇒-≤≤144a ⇒≤≤ 7．【答案】：B【解析】：如图，即A BCDE - 体积为214362432⨯⨯⨯⨯=8．【答案】：C【解析】：由题意知(,0)2p F ，不妨取双曲线的渐近线为b y x a =，由22b y x a y px⎧=⎪⎨⎪=⎩得222pa x b =.因为x AF ⊥，所以2A px =，即2222pa p x b ==，解得224b a =，即22224b a c a ==-，所以225c a =，即25e =，所以离心率e =9．【答案】：B【解析】：222222222cos ,cos ,cos ,222A B C b c a a c b a b c bc A ac B ab C ωωω+-+-+-======222222222A B b c a a c b c ωω+-+-+=+=，故A 正确，C 显然正确，1tan sin 2A ABC A bc A S ω∆==,同理，11tan ,tan 22B ABC C ABC B S C S ωω∆∆==，故D 正确 10．【答案】：A【解析】：令()()(1)()x f x xf x x x f x m ++=++=，x 为偶数时，1x +为奇数，当()f x 为偶数时m 才是偶数，故0的像有2个x 为奇数时，1x +为偶数，不论()f x 是偶数还是奇数，m 都是偶数，故1，1-的像都是5个则这样的映射f 有50个 填空题11．【答案】14【解析】z 取最大值的最优解为(1,1)，取最小值的最优解为(,)a a ，则z 的最大值为3，最小值为3a ，由334a =⋅，14a =12．【答案】10【解析】在51()(21)ax x x+-中令1x =，得12,1a a +==，51()(21)x x x+-中，5(21)x -展开式的通项为5515(1)2kkkk k T C x --+=-，则常数项为4415(1)210C -=13．【解析】直线l 0y -+=，圆C 的普通方程为22(2)1x y -+=，由点到直线的距离公式即可14．【答案】(1,)-+∞1232100(32)()2=⎰+=+=a x x dx x x ，设()()(24)F x f x x =-+,则(1)(1)(24)220F f -=---+=-=，'()'()2F x f x =-，对任意x R ∈，有'()'()20F x f x =->，即函数()F x 在R 上单调递增，则()0F x >的解集为(1,)-+∞，即()24f x x >+的解集为(1,)-+∞15．【答案】①③⑤【解析】作出函数()f x 的图象，(1)当0k -<时,1个不相等的实根 (2)当0k -=时,3个不相等的实根 (3)当01k <-<时，5个不相等的实根 (4)当1k -=时, 3个不相等的实根 (5)当1k ->时, 1个不相等的实根16．(本小题满分12分)【解析】：（1）由正弦定理得C R c B R b A R a sin 2,sin 2,sin 2===，则B C R B A R C B R cos sin 2cos sin 8cos sin 2-=， …………2分 故B C B A C B cos sin cos sin 4cos sin -=， 可得B A B C C B cos sin 4cos sin cos sin =+，即B A C B cos sin 4)sin(=+，可得B A A cos sin 4sin =， …………4分又0sin ≠A ，因此41cos =B ． …………6分（2）解：由2=⋅，可得2cos =B a ，又41cos =B ，故8=ac ． …………8分 又B ac c a b cos 2222-+=，可得1622=+c a ， …………10分 所以0)(2=-c a ，即c a =．所以22==c a ． …………12分17．(本小题满分12分)【解析】：(1)证明： ABC APB ∆⊥∆ 且交线为AB,又 PAB ∠为直角 所以ABC AP 平面⊥ 故 CM AP ⊥ 又 ABC ∆为等边三角形，点M 为AB 的中点 所以AB CM ⊥ 又 A AB PA =所以PAB CM 平面⊥ 又ABC CM ∆⊂所以平面P AB ⊥平面PCM ·········6分 （2）假设PA=a ，则AB=2aP M C B M B C P V V --=,PMC B MBC S h S PA ∙=∙3131,而三角形PMC 为直角三角形，故面积为226a ·故a h B 22=··················9分所以直线BP 与平面PMC 所成角的正弦值 sin B h PB θ==所以余弦值为10103cos =θ · ············12分 18 (本小题满分12分)解：（1）甲城市空气质量总体较好． …………………2分（2）甲城市在15天内空气质量类别为优或良的共有10天，任取1天，空气质量类别为优或良的概率为321510=， …………………3分乙城市在15天内空气质量类别为优或良的共有5天，任取1天，空气质量类别为优或良的概率为31155=， …………………4分在15天内任取1天，估计甲、乙两城市空气质量类别均为优或良的概率为923132=⨯． ……………………6分（3）X 的取值为2,1,0，…………………7分73)0(21521005===C C C X P ，2110)1(21511015===C C C X P ，212)0(21501025===C C C X P 所以X 的分布列为：…………………10分数学期望32212221101730=⨯+⨯+⨯=EX …………………12分19．（本小题满分13分）【解析】 (1)当1n =时时,由1121S a =-得113a =, 当 2≥n 时, 21n n S a =-①1121n n S a --=-②上面两式相减,得113n n a a -= 所以数列{}n a 是以首项为13,公比为13的等比数列,求得1()3nn a = ·········6分(2) 11331111log 11log ()13n n n b a n ===+++，nc====222nT=+=············13分20．（本小题满分13分）(Ⅰ) 由|PE|＋|PF|＝4＞|EF|及椭圆定义知，点P的轨迹是以E，F为焦点，4为长轴长的椭圆．设P(x，y)，则点P的轨迹方程为24x＋y2＝1．………… 5分(Ⅱ) 设圆P与圆F的另一个公共点为T，并设P(x0，y0)，Q(x1，y1)，T(x2，y2)，则由题意知，圆P的方程为(x－x0)2＋(y－y0)2＝x02＋y02．又Q为圆P与圆F的一个公共点，故22112222101000(5,()(),x yx x y y x y-+=-+-=+⎧⎨⎩所以(x0x1＋y0 y1－1＝0．同理(x0x2＋y0 y2－1＝0．因此直线QT的方程为(x0－x＋y0y－1＝0．连接PF交QT于H，则PF⊥QT．设|QH|＝d (d＞0)，则在直角△QHF中|FH||1|x-．又2214xy+=，故|FH|22==．在直角△QHF中d1=．所以点Q到直线PF的距离为1．………… 13分(第21题图)第11页（共11页）21. （本小题满分13分）(1)因为函数定义域为(0,)+∞，所以1ln 0ax x --≥即1ln x a x +≥，令1ln ()x g x x+=， 2ln ()0x g x-'==得1x = 因此max ()(1)1g x g ==，所以1a ≥ ………… 6分(2)由(1)知1a =时，1ln 0ax x --≥，即ln 1x x ≤-，则ln(1)x x +≤(当0x =时等号成立)，令1()x i N i *=∈，得11ln(1)i i+<，即1111,()i i i e e i i ++<<，取1,2,i n = ，并累乘得23123234(1)(1)123!n n n n n n e n n ++⋅⋅=<1 ，所以(1)!n n n n e +<，(1)!n n n e n +<e < ………… 13分。
安徽省合肥八中等2014届高三下学期联考（五）数学（理）试题扫描版含答案合肥八中2014年第三次适应性考试数学(理)参考答案选择题（5分×10＝50分）1．【答案】：B【解析】：1z i =--，22z i = 2．【答案】：D【解析】：2{|1}{|11}A x x x x x =>=><-或，2{|log 0}{|1}B x x x x =>=> 3．【答案】：A 【解析】：直线l 1：ax ＋2y －1＝0与直线l 2：x ＋(a ＋1)y ＋4＝0平行的充要条件是2a =-或1 4．【答案】：C 5．【答案】：A 【解析】：sin sin(2)sin[2()]6y x y x y x π=→=→=+6．【答案】：C【解析】：21222(log )(log )2(2)(log )(2)2log 2f a f a f f a f a +≤⇒≤⇒-≤≤144a ⇒≤≤ 7．【答案】：B 【解析】：如图，即A BCDE - 体积为214362432⨯⨯⨯⨯= 8．【答案】：C【解析】：由题意知(,0)2p F ，不妨取双曲线的渐近线为b y x a =，由22b y xay px⎧=⎪⎨⎪=⎩得222pa x b =.因为x AF ⊥，所以2A p x =，即2222pa px b ==，解得224b a =，即22224b a c a ==-，所以225c a =，即25e =，所以离心率e = 9．【答案】：B【解析】：222222222cos ,cos ,cos ,222A B C b c a a c b a b c bc A ac B ab C ωωω+-+-+-======222222222A B b c a a c b c ωω+-+-+=+=，故A 正确，C显然正确，1tan sin 2A ABC A bc A S ω∆==,同理，11tan ,tan 22B ABC C ABC B S C S ωω∆∆==，故D 正确10．【答案】：A【解析】：令()()(1)()x f x xf x x x f x m ++=++=，x 为偶数时，1x +为奇数，当()f x 为偶数时m 才是偶数，故0的像有2个x 为奇数时，1x +为偶数，不论()f x 是偶数还是奇数，m 都是偶数，故1，1-的像都是5个则这样的映射f 有50个 填空题11．【答案】14【解析】z 取最大值的最优解为(1,1)，取最小值的最优解为(,)a a ，则z 的最大值为3，最小值为3a ，由334a =⋅，14a = 12．【答案】10【解析】在51()(21)ax x x+-中令1x =，得12,1a a +==，51()(21)x x x+-中，5(21)x -展开式的通项为5515(1)2k k k k k T C x --+=-，则常数项为4415(1)210C -=13．【解析】直线l 0y -+=，圆C 的普通方程为22(2)1x y -+=，由点到直线的距离公式即可14．【答案】(1,)-+∞1232100(32)()2=⎰+=+=a x x dx x x ，设()()(24)F x f x x =-+,则(1)(1)(24)220F f -=---+=-=，'()'()2F x f x =-，对任意x R ∈，有'()'()20F x f x =->，即函数()F x 在R 上单调递增，则()0F x >的解集为(1,)-+∞，即()24f x x >+的解集为(1,)-+∞ 15．【答案】①③⑤【解析】作出函数()f x 的图象，(1)当0k -<时,1个不相等的实根(2)当0k -=时,3个不相等的实根(3)当01k <-<时，5个不相等的实根 (4)当1k -=时, 3个不相等的实根 (5)当1k ->时, 1个不相等的实根16．(本小题满分12分)【解析】：（1）由正弦定理得C R c B R b A R a sin 2,sin 2,sin 2===， 则B C R B A R C B R cos sin 2cos sin 8cos sin 2-=， (2)分故B C B A C B cos sin cos sin 4cos sin -=， 可得B A B C C B cos sin 4cos sin cos sin =+， 即BA CB cos sin 4)sin(=+，可得B A A cos sin 4sin =， …………4分又0sin ≠A ，因此41cos =B ．…………6分（2）解：由2=⋅，可得2cos =B a ，又41cos =B ，故8=ac ． …………8分又B ac c a b cos 2222-+=，可得1622=+c a ， …………10分所以0)(2=-c a ，即c a =． 所以22==c a ． …………12分17．(本小题满分12分)【解析】：(1)证明： ABC APB ∆⊥∆ 且交线为AB,又 PAB ∠为直角所以ABC AP 平面⊥ 故 CM AP ⊥ 又 ABC ∆为等边三角形，点M 为AB 的中点 所以AB CM ⊥ 又 A AB PA =所以PAB CM 平面⊥ 又ABC CM ∆⊂ 所以平面PAB ⊥平面PCM ·········6分 （2）假设PA=a ，则AB=2aP M C B M B C P V V --=,PMC B MBC S h S PA ∙=∙3131,而三角形PMC 为直角三角形，故面积为226a ·故a h B 22= ··················9分所以直线BP 与平面PMC 所成角的正弦值 sin B h PB θ==所以余弦值为10103cos =θ · ············12分18 (本小题满分12分)解：（1）甲城市空气质量总体较好．…………………2分（2）甲城市在15天内空气质量类别为优或良的共有10天，任取1天，空气质量类别为优或良的概率为321510=， …………………3分乙城市在15天内空气质量类别为优或良的共有5天，任取1天，空气质量类别为优或良的概率为31155=， …………………4分在15天内任取1天，估计甲、乙两城市空气质量类别均为优或良的概率为923132=⨯． ……………………6分（3）X 的取值为2,1,0，…………………7分73)0(21521005===C C C X P ，2110)1(21511015===C C C X P ，212)0(21501025===C C C X P 所以X 的分布列为：…………………10分数学期望32212221101730=⨯+⨯+⨯=EX…………………12分19．（本小题满分13分）【解析】 (1)当1n =时时,由1121S a =-得113a =, 当 2≥n 时, 21n n S a =-①1121n n S a --=-②上面两式相减,得113n n a a -= 所以数列{}n a 是以首项为13,公比为13的等比数列,求得1()3nn a = ····· (6)分 (2) 11331111log11log ()13n n n b a n ===+++，nc====22n T =············13分 20．（本小题满分13分）(Ⅰ) 由|PE |＋|PF |＝4＞|EF |及椭圆定义知，点P 的轨迹是以E ，F 为焦点，4为长轴长的椭圆．设P (x ，y )，则点P 的轨迹方程为24x＋y 2＝1． ………… 5分(Ⅱ) 设圆P 与圆F 的另一个公共点为T ，并设P (x 0，y 0)，Q (x 1，y 1)，T (x 2，y 2)，则由题意知，圆P 的方程为(x －x 0)2＋(y －y 0)2＝x 02＋y 02．又Q 为圆P 与圆F 的一个公共点，故22112222101000(5,()(),x y x x y y x y -+=-+-=+⎧⎨⎩ 所以(x 0x 1＋y 0 y 1－1＝0．同理(x 0x 2＋y 0 y 2－1＝0．因此直线QT 的方程为(x 0x ＋y 0y －1＝0．连接PF 交QT 于H ，则PF ⊥QT ．设|QH |＝d (d ＞0)，则在直角△QHF 中|FH ||1|x --．又220014x y +=，故|FH |22==．在直角△QHF 中d1=．所以点Q 到直线PF 的距离为1． ………… 13分21. （本小题满分13分）(1)因为函数定义域为(0,)+∞，所以1ln 0ax x --≥即1ln x a x +≥，令1ln ()xg x x+=， 2ln ()0xg x-'==得1x =(第21题图)因此max ()(1)1g x g ==，所以1a ≥ ………… 6分(2)由(1)知1a =时，1ln 0ax x --≥，即l n 1x x ≤-，则l n (1)x x +≤(当0x =时等号成立)，令1()x i N i *=∈，得11ln(1)i i+<，即1111,()i i i e e i i ++<<，取1,2,i n = ，并累乘得23123234(1)(1)123!nn nn n n en n ++⋅⋅=<1 ，所以(1)!n n n n e +<，(1)!n n n e n +<即e < ………… 13分。
河北衡水中学2013—2014学年度第一学期高三年级五调考试数学（理）试卷本试卷分为第I 卷（选择题）和第II 卷（非选择题）两部分.满分150分.考试时间120分钟.第Ⅰ卷（选择题 共60分）一、选择题：（每小题5分，共60分，下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上） 1. 设i 是虚数单位，则复数i－1＋i的虚部是( )A. －i 2 B ．－12 C.12 D ．i 22.已知命题x x R x p lg 2,:>-∈∃，命题0,:2>∈∀x R x q ，则( ) A.命题q p ∨是假命题 B.命题q p ∧是真命题 C.命题)(q p ⌝∧是真命题 D.命题)(q p ⌝∨是假命题3.一个几何体按比例绘制的三视图如图所示（单位：m ）, 则该几何体的体积为（ ）3m ． A ．37B.29C ．27D.494．以下四个命题中：①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测， 这样的抽样是分层抽样；②两个随机变量的线性相关性越强，则相关系数的绝对值越接近于1；③在某项测量中，测量结果ξ服从正态分布N (1，σ2)(σ＞0)．若ξ在(0,1)内取值的概率 为0.4，则ξ在(0,2)内取值的概率为0.8 ；④对分类变量X 与Y 的随机变量K 2的观测值k 来说，k 越小，判断“X 与Y 有关系”的把握程度越大．其中真命题的个数为( )A ．1B ．2C ．3D ．4 5. 已知等比数列{n a }的公比2=q ,且42a ,6a ,48成等差数列,则{n a }的前8项和为( )A ．127B ．255C ．511D ．10236．程序框图如图所示：如果上述程序运行的结果S ＝1320，那么判断框中应填入( ) A ．K ＜10? B ．K ≤10? C ．K <9? D ．K ≤11? 7.已知sin()sin 0,32ππααα++=-<<则2cos()3πα+等于（ ） A.45-B.35-C.45D.358.已知菱形ABCD 的边长为4，0051ABC =∠，若在菱形内任取一点，则该点到菱形的四个顶点的距离大于1的概率（ ） A.4π B. 41π- C. 8π D. 81π-9.函数|1|,1()1()1,12x a x f x x -=⎧⎪=⎨+≠⎪⎩若关于x 的方程22()(23)()30f x a f x a -++=有五个不同的实数解,则a 的取值范围是 （ ）A.(1,2)B.)2,23()23,1( C.3[,2)2 D. 3(1,)210.已知向量a ，b ，c 满足||||2a b a b ==⋅=，()(2)0a c b c -⋅-=，则||b c -的最小值为（ ）ABCD11.已知双曲线12222=-by a x 的左右焦点分别为12F F 、，O 为双曲线的中心，P 是双曲线右支上的点，21F PF ∆的内切圆的圆心为I ，且圆I 与x 轴相切于点A ，过2F 作直线PI 的垂线，垂足为B ，若e 为双曲线的离心率，则( )A. ||||OA e OB =B. ||||OB e OA =C. ||||OA OB =D. ||OA 与||OB 关系不确定 12．数列{}n a 共有12项，其中10a =，52a =，125a =，且11,1,2,3,11k k a a k +-==⋅⋅⋅，则满足这种条件的不同数列的个数为（ ）A.84B.168C.76D.152第Ⅱ卷 非选择题 （共90分）二、填空题（每小题5分，共20分. 每小题的答案填在答题纸的相应位置） 13.已知7270127()x m a a x a x a x -=++++的展开式中4x 的系数是－35，则1237a a a a ++++=14.已知f (x )是R 上的减函数，A (3，-1)，B (0，1)是其图象上两个点，则不等式|(1ln )|1f x +< 的解集是__________15.已知抛物线)1)0(22m M p px y ，（上一点>=到其焦点的距离为5，双曲线122=-ay x 的左顶点为A ，若双曲线一条渐近线与直线AM 垂直，则实数a=16.在棱长为1的正方体ABCD —A 1B 1C 1D 1中，M 、N 分别是AC 1、A 1B 1的中点．点P 在正方体的表面上运动，则总能使MP 与BN 垂直的点P 所构成的轨迹的周长等于 ．三、解答题（共70分.解答应写在答题纸的相应位置，并写出必要的文字说明、推理过程） 17. （本小题满分12分）已知圆O 的半径为R (R 为常数),它的内接三角形ABC 满足B b aC A R sin )2()sin (sin 222-=-成立,其中c b a ,,分别为C B A ∠∠∠,,的对边,求三角形ABC 面积S 的最大值.18.（本小题满分12分）某公司计划在迎春节联欢会中设一项抽奖活动：在一个不透明的口袋中装入外形一样号码分别为1，2，3，…，10的十个小球。
2014年考研数学一真题与解析一、选择题 1—8小题．每小题4分，共32分．１．下列曲线有渐近线的是（A ）x x y sin += （B ）x x y sin +=2（C ）xx y 1sin += （D ）x x y 12sin +=【分析】只需要判断哪个曲线有斜渐近线就可以．【详解】对于xx y 1sin +=，可知1=∞→x yx lim 且01==-∞→∞→x x y x x sin lim )(lim ，所以有斜渐近线x y = 应该选（C ）2．设函数)(x f 具有二阶导数，x f x f x g )())(()(110+-=，则在],[10上（ ）（A ）当0≥)('x f 时，)()(x g x f ≥ （B ）当0≥)('x f 时，)()(x g x f ≤（C ）当0≤'')(x f 时，)()(x g x f ≥ （D ）当0≤'')(x f 时，)()(x g x f ≤【分析】此题考查的曲线的凹凸性的定义及判断方法．【详解1】如果对曲线在区间],[b a 上凹凸的定义比较熟悉的话，可以直接做出判断．如果对区间上任意两点21x x ,及常数10≤≤λ，恒有())()()()(212111x f x f x x f λλλλ+-≥+-，则曲线是凸的． 显然此题中x x x ===λ,,1021，则=+-)()()(211x f x f λλ)()())((x g x f x f =+-110，而())()(x f x x f =+-211λλ，故当0≤'')(x f 时，曲线是凸的，即())()()()(212111x f x f x x f λλλλ+-≥+-，也就是)()(x g x f ≥，应该选（C ）【详解2】如果对曲线在区间],[b a 上凹凸的定义不熟悉的话，可令x f x f x f x g x f x F )())(()()()()(110---=-=，则010==)()(F F ，且)(")("x f x F =，故当0≤'')(x f 时，曲线是凸的，从而010==≥)()()(F F x F ，即0≥-=)()()(x g x f x F ，也就是)()(x g x f ≥，应该选（C ）３．设)(x f 是连续函数，则=⎰⎰---y y dy y x f dy 11102),(（Ａ）⎰⎰⎰⎰---+210011010x x dy y x f dx dy y x f dx ),(),(（Ｂ）⎰⎰⎰⎰----+010111012x x dy y x f dx dy y x f dx ),(),((Ｃ）⎰⎰⎰⎰+++θθππθθπθθθθθθsin cos sin cos )sin ,cos ()sin ,cos (1021020dr r r f d dr r r f d（Ｄ）⎰⎰⎰⎰+++θθππθθπθθθθθθsin cos sin cos )sin ,cos ()sin ,cos (1021020rdr r r f d rdr r r f d【分析】此题考查二重积分交换次序的问题，关键在于画出积分区域的草图． 【详解】积分区域如图所示如果换成直角坐标则应该是⎰⎰⎰⎰---+xx dy y x f dx dy y x f dx 10101012),(),(，（A ），（B ）两个选择项都不正确；如果换成极坐标则为⎰⎰⎰⎰+++θθππθθπθθθθθθsin cos sin cos )sin ,cos ()sin ,cos (1021020rdr r r f d rdr r r f d ．应该选（D ）４．若函数{}⎰⎰-∈---=--ππππdx x b x a x dx x b x a x Rb a 2211)sin cos (min )sin cos (,，则=+x b x a sin cos 11（Ａ）x sin 2 （Ｂ）x cos 2 （Ｃ）x sin π2 （Ｄ）x cos π2【详解】注意3232πππ=⎰-dx x ，222πππππ==⎰⎰--dx x dx x sin cos ，0==⎰⎰--dx x x dx x x ππππsin cos cos ，πππ2=⎰-dx x x sin ，所以b b a dx x b x a x πππππ42322232-++=--⎰-)()sin cos ( 所以就相当于求函数b b a 422-+的极小值点，显然可知当20==b a ,时取得最小值，所以应该选（A ）．５．行列式dc d c ba b a00000000等于（A ）2)(bc ad - （B ）2)(bc ad --（C ）2222c b d a - （D ）2222c b d a +- 【详解】20000000000000000)()()(bc ad bc ad bc bc ad ad dc ba bc d cb a addc c ba b d c d b a a dc d c ba b a --=-+--=+-=+-=应该选（B ）．6．设321ααα,, 是三维向量，则对任意的常数l k ,，向量31ααk +，32ααl +线性无关是向量321ααα,,线性无关的（A ）必要而非充分条件 （B ）充分而非必要条件 （C ）充分必要条件 （D ） 非充分非必要条件 【详解】若向量321ααα,,线性无关，则（31ααk +，32ααl +）K l k ),,(),,(3213211001αααααα=⎪⎪⎪⎭⎫⎝⎛=，对任意的常数l k ,，矩阵K 的秩都等于2，所以向量31ααk +，32ααl +一定线性无关．而当⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=000010001321ααα,,时，对任意的常数l k ,，向量31ααk +，32ααl +线性无关，但321ααα,,线性相关；故选择（A ）．7．设事件A ，B 想到独立，3050.)(,.)(=-=B A P B P 则=-)(A B P （ ）（A ）0.1 （B ）0.2 （C ）0.3 （D ）0.4【详解】)(.)(.)()()()()()(.)(A P A P A P B P A P A P AB P A P B A P 505030=-=-=-==-．所以60.)(=A P ，=-)(A B P 205050.)(..)()(=-=-A P AB P B P ．故选择（B ）．8．设连续型随机变量21X X ,相互独立，且方差均存在，21X X ,的概率密度分别为)(),(x f x f 21，随机变量1Y 的概率密度为))()(()(y f y f y f Y 21211+=，随机变量)(21221X X Y +=，则 （A ）2121DY DY EY EY >>, （B ）2121DY DY EY EY ==,（C ）2121DY DY EY EY <=, （D ）2121DY DY EY EY >=,【详解】())())()((2212112121Y E EX EX dy y f y f y EY =+=+=⎰+∞∞-，222121221212121EX EX dy y f y f y EY +=+=⎰+∞∞-))()((，()2212212121221222211221141414141412141412121DY X D X D X X E X D X D X E X E X E X E EX EX Y E Y E DY =+≥-++=---+=-=)()()()()()()()()()(故应该选择（D ）．二、填空题（本题共6小题，每小题4分，满分24分. 把答案填在题中横线上）9．曲面)sin ()sin (x y y x z -+-=1122在点),,(101处的切平面方程为 ．【详解】曲面)sin ()sin (x y y x z -+-=1122在点),,(101处的法向量为()),,(|,,),,(1121101--=-y xz z，所以切平面方程为0110112=--+--+-))(())(()(z y x ，即012=---z y x ．10．设)(x f 为周期为4的可导奇函数，且[]2012,),()('∈-=x x x f ，则=)(7f ．【详解】当[]20,∈x 时，C x x dx x x f +-=-=⎰2122)()(，由00=)(f 可知0=C ，即x x x f 22-=)(；)(x f 为周期为4奇函数，故1117==-=)()()(f f f ．11．微分方程0=-+)ln (ln 'y x y xy 满足31e y =)(的解为 ．【详解】方程的标准形式为x y x y dx dy ln =，这是一个齐次型方程，设xyu =，得到通解为1+=Cx xe y ，将初始条件31e y =)(代入可得特解为12+=x xe y ．12．设L 是柱面122=+y x 和平面0=+z y 的交线，从z 轴正方向往负方向看是逆时针方向，则曲线积分⎰=+Lydz zdx ．【详解】由斯托克斯公式⎰⎰⎰∑∂∂∂∂∂∂=++RQ P z y x dxdydzdx dydz Rdz Qdy Pdx L 可知π===+=+⎰⎰⎰⎰⎰⎰⎰∑∑xyD Ldxdy dxdy dzdx dydz ydz zdx ．其中⎩⎨⎧≤+=+∑1022y x z y :取上侧，{}122≤+=y x y x D xy |),(． 13．设二次型3231222132142x x x ax x x x x x f ++-=),,(的负惯性指数是1，则a 的取值范围是 ．【详解】由配方法可知232232231323122213214242xa x x ax x x x x ax x x x x x f )()()(),,(-+--+=++-=由于负惯性指数为1，故必须要求042≥-a ，所以a 的取值范围是[]22,-．14．设总体X 的概率密度为⎪⎩⎪⎨⎧<<=其它,,),(02322θθθθx xx f ，其中θ是未知参数，nX X X ,,, 21是来自总体的简单样本，若∑=ni iXC12是2θ的无偏估计，则常数C = ．【详解】22222532θθθθ==⎰2dx x x X E )(，所以21225θCn X C E n i i =⎪⎪⎭⎫ ⎝⎛∑=，由于∑=ni i X C 12是2θ的无偏估计，故125=Cn，nC 52=． 三、解答题15．（本题满分10分）求极限)ln())((limxx dt t e t x tx 1112112+--⎰+∞→．【分析】．先用等价无穷小代换简化分母，然后利用洛必达法则求未定型极限． 【详解】21121111111222121122112=⎪⎭⎫ ⎝⎛-++=--=--=+--∞→∞→+∞→+∞→⎰⎰x x o x x x x e x xdtt e t x x dtt e t x xx xtx x tx )((lim ))((lim ))((lim)ln())((lim16．（本题满分10分）设函数)(x f y =由方程06223=+++y x xy y 确定，求)(x f 的极值．【详解】解：在方程两边同时对x 求导一次，得到0223222=++++)(')(xy y y x xy y ， （１）即222232xxy y xyy dx dy ++--= 令0=dxdy及06223=+++y x xy y ，得到函数唯一驻点21-==y x ,． 在（１）式两边同时对x 求导一次，得到（022*******=+++++++y y x xy yy x xy y yy ")(')''(把0121=-==)(',,y y x 代入，得到0941>=)("y ， 所以函数)(x f y =在1=x 处取得极小值2-=y ．17．（本题满分10分）设函数)(u f 具有二阶连续导数，)cos (y e f z x=满足xx e y e z yz x z 222224)cos (+=∂∂+∂∂．若0000==)(',)(f f ，求)(u f 的表达式．【详解】 设y eu xcos =，则)cos ()(y e f u f z x ==，y e u f y e u f xze uf xzx x y x cos )('cos )(",)('cos +=∂∂=∂∂2222;y e u f y e u f yz y e u f y z x x xcos )('sin )(",sin )('-=∂∂-=∂∂2222； x x x e y e f e u f yzx z 222222)cos (")("==∂∂+∂∂ 由条件x x e y e z yzx z 222224)cos (+=∂∂+∂∂， 可知u u f u f +=)()("4这是一个二阶常用系数线性非齐次方程． 对应齐次方程的通解为：u u e C e C u f 2221-+=)(其中21C C ,为任意常数．对应非齐次方程特解可求得为u y 41-=*．故非齐次方程通解为u e C e C u f u u 412221-+=-)(．将初始条件0000==)(',)(f f 代入，可得16116121-==C C ,． 所以)(u f 的表达式为u e e u f u u 4116116122--=-)(． 18．（本题满分10分） 设曲面)(:122≤+=∑z y x z的上侧，计算曲面积分：dxdy z dzdx y dydz x )()()(11133-+-+-⎰⎰∑【详解】设⎩⎨⎧≤+=∑11221y x z :取下侧，记由1∑∑,所围立体为Ω，则高斯公式可得πθπ47373366733113131111210202222223321-=+-=++-=--++-=+-+--=-+-+-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩ∑+∑rdz r rdr d dxdydzy x dxdydz y x y x dxdydzy x dxdy z dzdx y dydz x )()()())()(()()()(在⎩⎨⎧≤+=∑11221y x z :取下侧上，0111111133=-=-+-+-⎰⎰⎰⎰∑∑dxdy dxdy z dzdx y dydz x )()()()(， 所以dz dy d yx )()()(11133-+-+-⎰⎰∑=π4111133-=-+-+-⎰⎰∑+∑dxdy z dzdx y dydz x )()()( 19．（本题满分10分）设数列{}{}n n b a ,满足2020ππ<<<<n n b a ,，n n nb a a cos cos =-且级数∑∞=1n n b 收敛．（1） 证明0=∞→n n a lim ；（2） 证明级数∑∞=1n nnb a 收敛． 【详解】（1）证明：由n n n b a a cos cos =-，及2020ππ<<<<n n b a ,可得20π<-=<n n n b a a cos cos ，所以20π<<<n n b a ，由于级数∑∞=1n nb收敛，所以级数∑∞=1n na也收敛，由收敛的必要条件可得0=∞→n n a lim ．（2）证明：由于2020ππ<<<<n n b a ,，所以2222nn n n n n n n a b a b b a b a -≤-+≤+sin ,sin222222222222nn n n n n n nn n n nnnn n nnn n n b b b b a b b a b b a b a b b a b b a b a =<-=-+≤-+=-=sin sincos cos由于级数∑∞=1n n b 收敛，由正项级数的比较审敛法可知级数∑∞=1n nnb a 收敛． 20．（本题满分11分）设⎪⎪⎪⎭⎫⎝⎛---=302111104321A ，E 为三阶单位矩阵．（1） 求方程组0=AX 的一个基础解系； （2） 求满足E AB =的所有矩阵．【详解】（1）对系数矩阵A 进行初等行变换如下：⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛----→⎪⎪⎪⎭⎫ ⎝⎛----→⎪⎪⎪⎭⎫ ⎝⎛---=310020101001310011104321134011104321302111104321A ，得到方程组0=AX 同解方程组⎪⎩⎪⎨⎧==-=43424132xx x x x x 得到0=AX 的一个基础解系⎪⎪⎪⎪⎪⎭⎫⎝⎛-=13211ξ． （2）显然B 矩阵是一个34⨯矩阵，设⎪⎪⎪⎪⎪⎭⎫⎝⎛=444333222111z y x z y x z y x z y x B 对矩阵)(AE 进行进行初等行变换如下：⎪⎪⎪⎭⎫⎝⎛-------→⎪⎪⎪⎭⎫ ⎝⎛------→⎪⎪⎪⎭⎫⎝⎛-----→⎪⎪⎪⎭⎫ ⎝⎛---=141310013120101621001141310001011100014321101134001011100014321100302101011100014321)(AE由方程组可得矩阵B 对应的三列分别为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1321011214321c x x x x ，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1321043624321c y y y y ，⎪⎪⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1321011134321c z z z z ， 即满足E AB =的所有矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛++-+-++-+-----=321321321321313431212321162c c cc c c c c c c c c B 其中321c c c ,,为任意常数． 21．（本题满分11分）证明n 阶矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛111111111与⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00200100 相似．【详解】证明：设=A ⎪⎪⎪⎪⎪⎭⎫⎝⎛111111111，=B ⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00200100． 分别求两个矩阵的特征值和特征向量如下：1111111111--=---------=-n n A E λλλλλλ)( ，所以A 的n 个特征值为0321====n n λλλλ ,；而且A 是实对称矩阵，所以一定可以对角化．且⎪⎪⎪⎪⎪⎭⎫⎝⎛00 λ~A ；1002010--=---=-n n nB E λλλλλλ)(所以B 的n 个特征值也为0321====n n λλλλ ,；对于1-n 重特征值0=λ，由于矩阵B B E -=-)(0的秩显然为1，所以矩阵B 对应1-n 重特征值0=λ的特征向量应该有1-n 个线性无关，进一步矩阵B 存在n 个线性无关的特征向量，即矩阵B 一定可以对角化，且⎪⎪⎪⎪⎪⎭⎫⎝⎛00 λ~B 从而可知n 阶矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛111111111 与⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00200100 相似．22．（本题满分11分）设随机变量X 的分布为2121====)()(X P X P ，在给定i X =的条件下，随机变量Y 服从均匀分布210,),,(=i i U ． （1） 求Y 的分布函数； （2） 求期望).(Y E 【详解】（1）分布函数())/()/()()/()()/(),(),()()(2121221121=≤+=≤===≤+==≤==≤+=≤=≤=X y Y P X y Y P X P X y Y P X P X y Y P X y Y P X y Y P y Y P y F当0<y 时，0=)(y F ；当10<≤y 时，y y y y F 4322121=+=)(； 当21<≤y 时，214122121+=+=y y y F )(；当2≥y 时，1=)(y F ．所以分布函数为⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤+<≤<=2121421104300y y y y y y y F ,,,,)( （2）概率密度函数为⎪⎪⎪⎩⎪⎪⎪⎨⎧<<<<==其它,,,)(')(021411043y y y F y f ，434432110=+=⎰⎰dy y ydy Y E )(． 23．（本题满分11分）设总体X 的分布函数为⎪⎩⎪⎨⎧<≥-=-00012x x ex F x ,,),(θθ，其中θ为未知的大于零的参数，n X X X ,,, 21是来自总体的简单随机样本，（1）求)(),(2XE X E ；（2）求θ的极大似然估计量．（３）是否存在常数a ，使得对任意的0>ε，都有0=⎭⎬⎫⎩⎨⎧≥-∞→εθa P n n ^lim ．【详解】（１）先求出总体X 的概率密度函数⎪⎩⎪⎨⎧<≥=-00022x x e x x f x,,),(θθθ，πθθθθθθ=+-=-==⎰⎰⎰∞+-∞+--∞+∞+-dx exedex dx exEX x x x x 000222222|；;θθθθθθθ====⎰⎰⎰∞+--∞+∞+-dt te dx ex dx exEX tx x 020203211222（２）极大似然函数为⎪⎪⎩⎪⎪⎨⎧≥∑∏=∏==-==其它,,),()(0021211i x i ni n n i n i x e x x f L ni i θθθθ当所有的观测值都大于零时，∑∑==--+=ni ini ixn xn LnL 12112θθθln ln ln )(，令0=θθd L d )(ln ，得θ的极大似然估计量为nxni i∑==12^θ；（３）因为n X X X ,,, 21独立同分布，显然对应的22221nX X X ,,, 也独立同分布，又有（１）个可知θ=2iEX ，由辛钦大数定律，可得0112=⎭⎬⎫⎩⎨⎧≥-∑=∞→εn i i i n EX x n P lim ，由前两问可知，nxni i∑==12^θ，θ=2iEX ，所以存在常数θ=a ，使得对任意的0>ε，都有0=⎭⎬⎫⎩⎨⎧≥-∞→εθa P n n ^lim ． 2014年考研数学二真题与解析一、选择题 1—8小题．每小题4分，共32分．１．当+→0x 时，若)(lnx 21+α，α11)cos (x -均是比x 高阶的无穷小，则α的可能取值范围是（ ）（A ）),(+∞2 （B ）),(21 （C ）),(121 （D ）),(210 【详解】αααx x 221~)(ln+，是α阶无穷小，ααα211211x x ~)cos (-是α2阶无穷小，由题意可知⎪⎩⎪⎨⎧>>121αα所以α的可能取值范围是),(21，应该选（B ）．2．下列曲线有渐近线的是（A ）x x y sin += （B ）x x y sin +=2（C ）xx y 1sin += （D ）x x y 12sin +=【详解】对于xx y 1sin +=，可知1=∞→x yx lim 且01==-∞→∞→x x y x x sin lim )(lim ，所以有斜渐近线x y = 应该选（C ）3．设函数)(x f 具有二阶导数，x f x f x g )())(()(110+-=，则在],[10上（ ）（A ）当0≥)('x f 时，)()(x g x f ≥ （B ）当0≥)('x f 时，)()(x g x f ≤（C ）当0≥'')(x f 时，)()(x g x f ≥ （D ）当0≥'')(x f 时，)()(x g x f ≤【分析】此题考查的曲线的凹凸性的定义及判断方法．【详解1】如果对曲线在区间],[b a 上凹凸的定义比较熟悉的话，可以直接做出判断． 显然x f x f x g )())(()(110+-=就是联接))(,()),(,(1100f f 两点的直线方程．故当0≥'')(x f 时，曲线是凹的，也就是)()(x g x f ≤，应该选（D ）【详解2】如果对曲线在区间],[b a 上凹凸的定义不熟悉的话，可令x f x f x f x g x f x F )())(()()()()(110---=-=，则010==)()(F F ，且)(")("x f x F =，故当0≥'')(x f 时，曲线是凹的，从而010==≤)()()(F F x F ，即0≤-=)()()(x g x f x F ，也就是)()(x g x f ≤，应该选（D ）4．曲线⎩⎨⎧++=+=14722t t y t x ,上对应于1=t 的点处的曲率半径是（ ）（Ａ）5010（Ｂ）10010 (Ｃ）1010 （Ｄ）105 【详解】 曲线在点))(,(x f x 处的曲率公式321)'("y y K +=，曲率半径KR 1=． 本题中422+==t dt dy t dt dx ,，所以t t t dx dy 21242+=+=，3222122tt t dx y d -=-=，对应于1=t 的点处13-==",'y y ，所以10101132=+=)'("y y K ，曲率半径10101==KR ． 应该选（C ）5．设函数x x f arctan )(=，若)(')(ξxf x f =，则=→22xx ξlim（ ）（Ａ）1 （Ｂ）32 （Ｃ）21 （Ｄ）31 【详解】注意（1）211xx f +=)('，（2）)(arctan ,33310x o x x x x +-=→时．由于)(')(ξxf x f =．所以可知x x x x f f arctan )()('==+=211ξξ，22)(arctan arctan x x x -=ξ， 31313332022=+--=-=→→→x x o x x x x x xarx x x x x x )()(lim)(arctan tan limlimξ． 6．设),(y x u 在平面有界闭区域D 上连续，在D 的内部具有二阶连续偏导数，且满足02≠∂∂∂y x u及02222=∂∂+∂∂yu x u ，则（ ）．（A ）),(y x u 的最大值点和最小值点必定都在区域D 的边界上；（B ）),(y x u 的最大值点和最小值点必定都在区域D 的内部；（C ）),(y x u 的最大值点在区域D 的内部，最小值点在区域D 的边界上；（D ）),(y x u 的最小值点在区域D 的内部，最大值点在区域D 的边界上．【详解】),(y x u 在平面有界闭区域D 上连续，所以),(y x u 在D 内必然有最大值和最小值．并且如果在内部存在驻点),(00y x ，也就是0=∂∂=∂∂yux u ，在这个点处x y u y x u B yu C x u A ∂∂∂=∂∂∂=∂∂=∂∂=222222,,，由条件，显然02<-B AC ，显然),(y x u 不是极值点，当然也不是最值点，所以),(y x u 的最大值点和最小值点必定都在区域D 的边界上．所以应该选（A ）．7．行列式dc d c ba b a00000000等于（A ）2)(bc ad - （B ）2)(bc ad -- （C ）2222c b d a - （D ）2222c b d a +- 【详解】20000000000000000)(bc ad dc ba bc d cb a ad dc c ba b d c d b a a dc d c b a b a --=+-=+-=应该选（B ）．8．设321ααα,, 是三维向量，则对任意的常数l k ,，向量31ααk +，32ααl +线性无关是向量321ααα,,线性无关的（A ）必要而非充分条件 （B ）充分而非必要条件 （C ）充分必要条件 （D ） 非充分非必要条件 【详解】若向量321ααα,,线性无关，则（31ααk +，32ααl +）K l k ),,(),,(3213211001αααααα=⎪⎪⎪⎭⎫ ⎝⎛=，对任意的常数l k ,，矩阵K 的秩都等于2，所以向量31ααk +，32ααl +一定线性无关．而当⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=000010001321ααα,,时，对任意的常数l k ,，向量31ααk +，32ααl +线性无关，但321ααα,,线性相关；故选择（A ）．二、填空题（本题共6小题，每小题4分，满分24分. 把答案填在题中横线上）9．⎰∞-=++12521dx x x ．【详解】⎰⎰∞-∞-∞-=⎪⎭⎫ ⎝⎛--=+=++=++11122832421212141521πππ)(|arctan )(x x dx dx x x ． 10．设)(x f 为周期为4的可导奇函数，且[]2012,),()('∈-=x x x f ，则=)(7f ．【详解】当[]20,∈x 时，C x x dx x x f +-=-=⎰2122)()(，由00=)(f 可知0=C ，即x x x f 22-=)(；)(x f 为周期为4奇函数，故1117==-=)()()(f f f ．11．设),(y x z z =是由方程4722=+++z y x eyz确定的函数，则=⎪⎭⎫ ⎝⎛2121,|dz ．【详解】设4722-+++=z y x ez y x F yz),,(，1222122+=+==yz z yz y x ye F y ze F F ,,，当21==y x 时，0=z ，21-=-=∂∂z x F F x z ，21-=-=∂∂z y F F y z ，所以=⎪⎭⎫ ⎝⎛2121,|dz dy dx 2121--．12．曲线L 的极坐标方程为θ=r ，则L 在点⎪⎭⎫⎝⎛=22ππθ,),(r 处的切线方程为 ．【详解】先把曲线方程化为参数方程⎩⎨⎧====θθθθθθθθsin sin )(cos cos )(r y r x ，于是在2πθ=处，20π==y x ,，πθθθθθθππ222-=-+=|sin cos cos sin |dx dy ，则L 在点⎪⎭⎫⎝⎛=22ππθ,),(r 处的切线方程为)(022--=-x y ππ，即.22ππ+-=x y13．一根长为1的细棒位于x 轴的区间[]10,上，若其线密度122++-=x x x )(ρ，则该细棒的质心坐标=x ．【详解】质心坐标20113512111221021023101==++-++-==⎰⎰⎰⎰dx x x dxx x x dx x dxx x x )()()()(ρρ． 14．设二次型3231222132142x x x ax x x x x x f ++-=),,(的负惯性指数是1，则a 的取值范围是 ． 【详解】由配方法可知232232231323122213214242xa x x ax x x x x ax x x x x x f )()()(),,(-+--+=++-=由于负惯性指数为1，故必须要求042≥-a ，所以a 的取值范围是[]22,-．三、解答题15．（本题满分10分）求极限)ln())((limxx dt t e t x tx 1112112+--⎰+∞→．【分析】．先用等价无穷小代换简化分母，然后利用洛必达法则求未定型极限． 【详解】21121111111222121122112=⎪⎭⎫ ⎝⎛-++=--=--=+--∞→∞→+∞→+∞→⎰⎰x x o x x x x e x xdtt e t xx dt t e t x xx xtx x tx )((lim ))((lim ))((lim)ln())((lim16．（本题满分10分）已知函数)(x y y =满足微分方程''y y y x-=+122，且02=)(y ，求)(x y 的极大值和极小值． 【详解】解：把方程化为标准形式得到2211x dxdyy -=+)(，这是一个可分离变量的一阶微分方程，两边分别积分可得方程通解为：C x x y y +-=+333131，由02=)(y 得32=C ， 即32313133+-=+x x y y ． 令01122=+-=y x dx dy ，得1±=x ，且可知3222222211212)()()(y x y y x dx y d +--+-=； 当1=x 时，可解得1=y ，01<-="y ，函数取得极大值1=y ；当1-=x 时，可解得0=y ，02>="y ，函数取得极小值0=y ．17．（本题满分10分）设平面区域{}004122≥≥≤+≤=y x y x y x D .,|),(．计算⎰⎰++Ddxdy y x y x x )sin(22π 【详解】由对称性可得432112121212022222222-==+=+++=++=++⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰D D D Ddr r r d dxd y x dxdy y x y x y x dxd y x y x y dxd y x y x x πθπππππsin )sin()sin()()sin()sin(18．（本题满分10分）设函数)(u f 具有二阶连续导数，)cos (y e f z x=满足xx e y e z yz x z 222224)cos (+=∂∂+∂∂．若0000==)(',)(f f ，求)(u f 的表达式．【详解】 设y eu xcos =，则)cos ()(y e f u f z x ==，y e u f y e u f xz e u f xzxx y x cos )('cos )(",)('cos +=∂∂=∂∂2222; y e u f y e u f yz y e u f y z xx x cos )('sin )(",sin )('-=∂∂-=∂∂2222； xx x e y e f e u f yz x z 222222)cos (")("==∂∂+∂∂ 由条件xx e y e z yz x z 222224)cos (+=∂∂+∂∂， 可知u u f u f +=)()("4这是一个二阶常用系数线性非齐次方程． 对应齐次方程的通解为：u u e C e C u f 2221-+=)(其中21C C ,为任意常数．对应非齐次方程特解可求得为u y 41-=*．故非齐次方程通解为u e C e C u f u u 412221-+=-)(．将初始条件0000==)(',)(f f 代入，可得16116121-==C C ,． 所以)(u f 的表达式为u e e u f u u 4116116122--=-)(．19．（本题满分10分） 设函数)(),(x g x f 在区间[]b a .上连续，且)(x f 单调增加，10≤≤)(x g ，证明：（3） []b a x a x dt t g xa,,)(∈-≤≤⎰0；（4）⎰⎰≤⎰+badtt g a adx x g x f dx x f ba )()()()(．【详解】（1）证明：因为10≤≤)(x g ，所以[]b a x dt dt t g dx xax axa,)(∈≤≤⎰⎰⎰10．即[]b a x a x dt t g xa,,)(∈-≤≤⎰0．（2）令⎰⎰⎰-=+xa dtt g a axadu u f du u g u f x F )()()()()(，则可知0=)(a F ，且⎪⎭⎫ ⎝⎛+-=⎰xadt t g a f x g x g x f x F )()()()()('，因为,)(a x dt t g xa-≤≤⎰0且)(x f 单调增加，所以)()()(x f a x a f dt t g a f xa =-+≤⎪⎭⎫ ⎝⎛+⎰．从而0=-≥⎪⎭⎫ ⎝⎛+-=⎰)()()()()()()()()('x f x g x g x f dt t g a f x g x g x f x F xa ，[]b a x ,∈ 也是)(x F 在[]b a ,单调增加，则0=≥)()(a F b F ，即得到⎰⎰≤⎰+badtt g a adx x g x f dx x f ba )()()()(．20．（本题满分11分）设函数[]101,,)(∈+=x xxx f ，定义函数列 )()(x f x f =1，))(()(x f f x f 12=， )),(()(,x f f x f n n 1-=设n S 是曲线)(x f y n =，直线01==y x ,所围图形的面积．求极限n n nS ∞→lim ．【详解】x xxx x xx f x f x f x x x f 21111111121+=+++=+=+=)()()(,)(， ,)(x x x f 313+=， 利用数学归纳法可得.)(nxxx f n +=1))ln(()()(nn n dx nx n dx nx x dx x f S n n +-=+-=+==⎰⎰⎰1111111110101，111=⎪⎭⎫ ⎝⎛+-=∞→∞→n n nS n n n )ln(lim lim ． 21．（本题满分11分）已知函数),(y x f 满足)(12+=∂∂y yf，且y y y y y f ln )()(),(--+=212，求曲线0=),(y x f 所成的图形绕直线1-=y 旋转所成的旋转体的体积．【详解】由于函数),(y x f 满足)(12+=∂∂y yf，所以)(),(x C y y y x f ++=22，其中)(x C 为待定的连续函数．又因为y y y y y f ln )()(),(--+=212，从而可知y y y C ln )()(--=21，得到x x y y x C y y y x f ln )()(),(--++=++=212222．令0=),(y x f ，可得x x y ln )()(-=+212．且当1-=y 时，2121==x x ,．曲线0=),(y x f 所成的图形绕直线1-=y 旋转所成的旋转体的体积为πππ)ln (ln )()(45222121212-=-=+=⎰⎰dx x x dx y V22．（本题满分11分）设⎪⎪⎪⎭⎫ ⎝⎛---=302111104321A ，E 为三阶单位矩阵．（3） 求方程组0=AX 的一个基础解系； （4） 求满足E AB =的所有矩阵．【详解】（1）对系数矩阵A 进行初等行变换如下：⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛----→⎪⎪⎪⎭⎫ ⎝⎛----→⎪⎪⎪⎭⎫ ⎝⎛---=310020101001310011104321134011104321302111104321A ，得到方程组0=AX 同解方程组⎪⎩⎪⎨⎧==-=43424132xx x x x x 得到0=AX 的一个基础解系⎪⎪⎪⎪⎪⎭⎫⎝⎛-=13211ξ．（2）显然B 矩阵是一个34⨯矩阵，设⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=444333222111z y x z y xz y x z y x B 对矩阵)(AE 进行进行初等行变换如下：⎪⎪⎪⎭⎫⎝⎛-------→⎪⎪⎪⎭⎫ ⎝⎛------→⎪⎪⎪⎭⎫⎝⎛-----→⎪⎪⎪⎭⎫ ⎝⎛---=141310013120101621001141310001011100014321101134001011100014321100302101011100014321)(AE由方程组可得矩阵B 对应的三列分别为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1321011214321c x x x x ，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1321043624321c y y y y ，⎪⎪⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1321011134321c z z z z ， 即满足E AB =的所有矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛++-+-++-+-----=321321321321313431212321162c c cc c c c c c c c c B其中321c c c ,,为任意常数． 23．（本题满分11分）证明n 阶矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛111111111与⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00200100 相似． 【详解】证明：设=A ⎪⎪⎪⎪⎪⎭⎫⎝⎛111111111，=B ⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00200100． 分别求两个矩阵的特征值和特征向量如下：1111111111--=---------=-n n A E λλλλλλ)( ，所以A 的n 个特征值为0321====n n λλλλ ,；而且A 是实对称矩阵，所以一定可以对角化．且⎪⎪⎪⎪⎪⎭⎫⎝⎛00 λ~A ； 1002010--=---=-n n nB E λλλλλλ)(所以B 的n 个特征值也为0321====n n λλλλ ,；对于1-n 重特征值0=λ，由于矩阵B B E -=-)(0的秩显然为1，所以矩阵B 对应1-n 重特征值0=λ的特征向量应该有1-n 个线性无关，进一步矩阵B 存在n 个线性无关的特征向量，即矩阵B 一定可以对角化，且⎪⎪⎪⎪⎪⎭⎫⎝⎛00 λ~B从而可知n 阶矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛111111111 与⎪⎪⎪⎪⎪⎭⎫⎝⎛n 00200100 相似． 2014年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸．．．指定位置上.（1）设lim ,n a a =且0,a ≠则当n 充分大时有（ ）（A ）2n aa >（B ）2n a a <（C ）1n a a n >-（D ）1n a a n<+（2）下列曲线有渐近线的是（ ）（A ）sin y x x =+ （B ）2sin y x x =+（C ）1sin y x x =+（D ）21sin y x x=+（3）设23(x)a P bx cx dx =+++ ，当0x → 时，若(x)tanx P - 是比x 3高阶的无穷小，则下列试题中错误的是 （A ）0a = （B ）1b = （C ）0c =（D ）16d =（4）设函数()f x 具有二阶导数，()(0)(1)(1)g x f x f x =-+，则在区间[0,1]上（ ） （A ）当'()0f x ≥时，()()f x g x ≥ （B ）当'()0f x ≥时，()()f x g x ≤ （C ）当'()0f x ≤时，()()f x g x ≥ （D ）当'()0f x ≤时，()()f x g x ≥（5）行列式0000000a b abc d cd=（A ）2()ad bc - （B ）2()ad bc -- （C ）2222a d b c - （D ）2222b c a d -（6）设123,,a a a 均为3维向量，则对任意常数,k l ，向量组1323,k l αααα++线性无关是向量组123,,ααα线性无关的 （A ）必要非充分条件 （B ）充分非必要条件 （C ）充分必要条件 （D ）既非充分也非必要条件（7）设随机事件A 与B 相互独立，且P （B ）=0.5，P(A-B)=0.3，求P （B-A ）=（ ） （A ）0.1 （B ）0.2 （C ）0.3 （D ）0.4（8）设123,,X X X 为来自正态总体2(0,)N σ的简单随机样本，服从的分布为 （A ）F （1,1） （B ）F （2,1） （C ）t(1） （D ）t(2)二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸．．．指定位置上. （9）设某商品的需求函数为402Q P =-（P 为商品价格），则该商品的边际收益为_________。
一、填空题（每小题3分，共15分） 1、极限2sin 0lim(13)x x x →+= ．2、设2arctan()y x x =，则y ' ． 3、设()f x 的一个原函数为2x e-，则()________xf x dx '=⎰．4、曲线xe y =过原点的切线方程为____________． 5、曲线2r eθ=从0=θ至2πθ=的一段弧长=l ____________．二、选择题（每小题3分，共15分） 1、当1x →-时，31x +与3(1)x +为（）(A) 高阶无穷小 (B) 低阶无穷小(C) 等价无穷小 (D) 同阶但不等价无穷小2、若()f x 的导函数为sin ,x 则()f x 的一个原函数是（ ）(A) 1sin x + (B) 1sin x - (C) 1cos x + (D) 1cos x -3、设()f x 在0x =处连续，且0()lim 11cos x f x x→=-，则在点0x =处（ ）． (A) (0)f '不存在 (B) (0)0f '=，且(0)f 为()f x 的极小值 (C) (0)f '存在，且(0)0f '≠ (D) (0)0f '=，且(0)f 为()f x 的极大值4、下列广义积分发散的是（ ）(A)1+∞⎰(B)111sin dx x -⎰ (C)221ln dx x x+∞⎰(D) 2x xe dx +∞--∞⎰5、曲线2211x x e y e--+=-（）(A) 没有渐近线 (B) 仅有水平渐近线 (C) 仅有铅直渐近线 (D) 既有水平渐近线又有铅直渐近线三、计算下列各题（每小题6分，共36分）1、222111lim ()2n n n n n n πππ→∞++++++L ． 2、)cos 1)(1(1cossin 3lim 20x e x x x xx +---→． 3、求sin (0)xy xx =>的导数()y x '． 4、已知()2ln 1,arctan ,x t y t ⎧=+⎪⎨=⎪⎩求22d d ,d d y yx x ． 5、2arctan x dx x ⎰． ６、设2ln(1)0()101x x f x x x +≥⎧⎪=⎨<⎪+⎩，求20(1)f x dx -⎰． 四、（本题满分10分）设 ()()22021cos , 0, 1, 0,1cos d , 0,xx x x f x x t t x x ⎧-<⎪⎪==⎨⎪⎪>⎩⎰ 讨论()f x 在0x =处的连续性和可导性．五、（本题满分10分）设曲线2xe y =，切线2ey x =及y 轴围成的平面图形为D ，求D 绕y 轴旋转一周所得旋转体体积V .六、（本题满分8分）证明不等式：0>x 时，有11ln ≥+xx . 七、（本题满分6分）设函数)(x f 在]1,0[上连续，在)1,0(内可导，0)(≠x f （01x <<），且0)1()0(==f f ，证明：在)1,0(内至少存在一点ξ，使()2015()f f ξξ'=．。
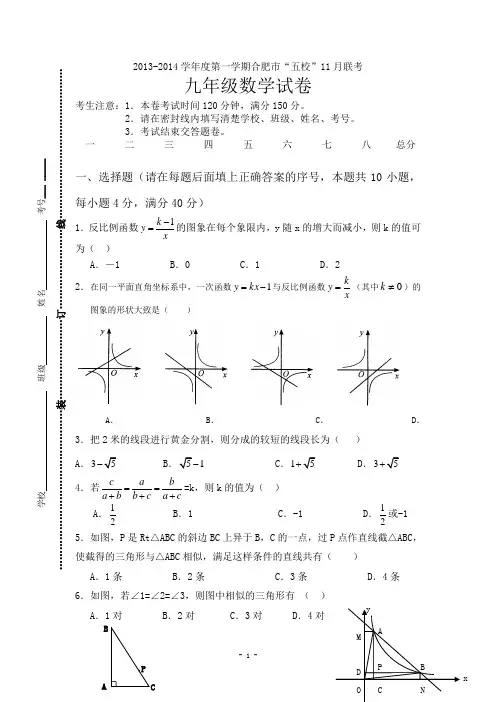
2013-2014学年度第一学期合肥市“五校”11月联考九年级数学试卷1．本卷考试时间120分钟，满分150分。
．请在密封线内填写清楚学校、班级、姓名、考号。
．考试结束交答题卷。
二 三 四 五 六 七 八 总分10小题，4分，满分40分）反比例函数1k y x-=的图象在每个象限内，y 随x 的增大而减小，则k 的值可 ）A ．－1B ．0C ．1D ．2 在同一平面直角坐标系中，一次函数1-=kx y 与反比例函数xky =（其中0≠k ）的图象的形状大致是（ ）A ．B ．C ．D ．2米的线段进行黄金分割，则分成的较短的线段长为（ ）31 C ．1 D ．3+c a ba b b c a c ==+++=k ，则k 的值为（ ） A ．12 B ．1 C ．-1 D ．12或-1P 是Rt △ABC 的斜边BC 上异于B ，C 的一点，过P 点作直线截△ABC ，ABC 相似，满足这样条件的直线共有（ ） A ．1条 B ．2条 C ．3条 D ．4条 1=∠2=∠3，则图中相似的三角形有 （ ）A ．1对 B ．2对 C ．3对 D ．4对（第5题） （第6题） （第7题） （第10题） 7．梯形ABCD 中，AD ∥BC ，对角线AC 、BD 相交于O 点，若AOD S ∆∶ACD S ∆＝1∶3，则AOD S ∆∶BOC S ∆＝（ ）． A ．61 B ．31 C ．41D ．66 8．下图中阴影部分的面积与函数2122y x x =-++的最大值相同的是（ ）9．已知二次函数()2111y x bx b =-+-≤≤，当b 从1-逐渐变化到的过程中，它所对应的抛物线位置也随之变动．关于抛物线的移动方向的描述中，正确的是（ ）A ．先往左上方移动，再往左下方移动 B ．先往左下方移动，再往左上方移动C ．先往右上方移动，再往右下方移动D ．先往右下方移动，再往右上方移动10．已知反比例函数(0)ky k x=>的图象与一次函数6y x =-+相交与第一象限的A 、B 两点，如图所示，过A 、B 两点分别做x 、y 轴的垂线，线段AC 、BD 相交与P ，给出以下结论：①OA=OB ；②OAM OBN ∆∆∽；③若ABP ∆的面积是8，则5k =；④P 点一定在直线y x =上，其中正确命题的个数是（ ）个 A ．1 B ．2 C ．3 D ．411．如图，在△ABC 中，D 为AC 边上一点，要使CBD CAB ∆∆∽,需添加一个条件是________12．如图，点O 是等边三角形PQR 的中心，P′、Q′、R′分别是OP 、OQ 、OR 的中点，则△P′Q′R′与△PQR 是位似三角形．此时，△P′Q′R′与△PQR 的位似比为_________13．已知函数1y x=，当x <-1时，函数y 的取值范围是________14．如图，已知反比例函数xy 1=的图像上有一点P ，过点P 分别作x 轴和y 轴的垂线，垂足分别为A 、B ，使四边形OAPB 为正方形。
合肥八中2014年第三次适应性考试数学(理)参考答案选择题（5分×10＝50分）1．【答案】：B【解析】：1z i =--，22z i = 2．【答案】：D【解析】：2{|1}{|11}A x x x x x =>=><-或，2{|log 0}{|1}B x x x x =>=> 3．【答案】：A 【解析】：直线l 1：ax ＋2y －1＝0与直线l 2：x ＋(a ＋1)y ＋4＝0平行的充要条件是2a =-或1 4．【答案】：C 5．【答案】：A 【解析】：sin sin(2)sin[2()]6y x y x y x π=→=→=+6．【答案】：C【解析】：21222(log )(log )2(2)(log )(2)2log 2f a f a f f a f a +≤⇒≤⇒-≤≤144a ⇒≤≤ 7．【答案】：B 【解析】：如图，即A BCDE - 体积为214362432⨯⨯⨯⨯= 8．【答案】：C【解析】：由题意知(,0)2p F ，不妨取双曲线的渐近线为b y x a =，由22b y xay px⎧=⎪⎨⎪=⎩得222pa x b =.因为x AF ⊥，所以2A px =，即2222pa p x b ==，解得224b a =，即22224b a c a ==-，所以225c a =，即25e =，所以离心率e = 9．【答案】：B【解析】：222222222cos ,cos ,cos ,222A B C b c a a c b a b c bc A ac B ab C ωωω+-+-+-======222222222A B b c a a c b c ωω+-+-+=+=，故A 正确，C显然正确，1tan sin 2A ABC A bc A S ω∆==,同理，11tan ,tan 22B ABC C ABC B S C S ωω∆∆==，故D 正确10．【答案】：A【解析】：令()()(1)()x f x xf x x x f x m ++=++=，x 为偶数时，1x +为奇数，当()f x 为偶数时m 才是偶数，故0的像有2个x 为奇数时，1x +为偶数，不论()f x 是偶数还是奇数，m 都是偶数，故1，1-的像都是5个则这样的映射f 有50个 填空题11．【答案】14【解析】z 取最大值的最优解为(1,1)，取最小值的最优解为(,)a a ，则z 的最大值为3，最小值为3a ，由334a =⋅，14a = 12．【答案】10【解析】在51()(21)ax x x +-中令1x =，得12,1a a +==，51()(21)x x x+-中，5(21)x -展开式的通项为5515(1)2kk k k k T C x --+=-，则常数项为4415(1)210C -=13．【解析】直线l 0y -+=，圆C 的普通方程为22(2)1x y -+=，由点到直线的距离公式即可14．【答案】(1,)-+∞1232100(32)()2=⎰+=+=a x x dx x x ，设()()(24)F x f x x =-+,则(1)(1)(24)220F f -=---+=-=，'()'()2F x f x =-，对任意x R ∈，有'()'()20F x f x =->，即函数()F x 在R 上单调递增，则()0F x >的解集为(1,)-+∞，即()24f x x >+的解集为(1,)-+∞ 15．【答案】①③⑤【解析】作出函数()f x 的图象，(1)当0k -<时,1个不相等的实根(2)当0k -=时,3个不相等的实根(3)当01k <-<时，5个不相等的实根 (4)当1k -=时, 3个不相等的实根 (5)当1k ->时, 1个不相等的实根16．(本小题满分12分)【解析】：（1）由正弦定理得C R c B R b A R a sin 2,sin 2,sin 2===， 则B C R B A R C B R cos sin 2cos sin 8cos sin 2-=， …………2分故B C B A C B cos sin cos sin 4cos sin -=， 可得B A B C C B cos sin 4cos sin cos sin =+，即B AC B cos sin 4)sin(=+，可得B A A c o s s i n 4s i n =， …………4分又0sin ≠A ，因此41c o s =B ．…………6分（2）解：由2=⋅BC BA ，可得2cos =B a ，又41cos =B ，故8=ac ． …………8分又B ac c a b cos 2222-+=， 可得1622=+c a ， (10)分所以0)(2=-c a ，即c a =．所以22==c a ． …………12分17．(本小题满分12分)【解析】：(1)证明： ABC APB ∆⊥∆ 且交线为AB,又 PAB ∠为直角所以ABC AP 平面⊥ 故 CM AP ⊥ 又 ABC ∆为等边三角形，点M 为AB 的中点 所以AB CM ⊥ 又 A AB PA =所以PAB CM 平面⊥ 又ABC CM ∆⊂所以平面P AB ⊥平面PCM ·········6分 （2）假设PA=a ，则AB=2aPMC B MBC P V V --=,PMC B MBC S h S PA ∙=∙3131,而三角形PMC 为直角三角形，故面积为226a ·故a h B 22= ··················9分所以直线BP 与平面PMC 所成角的正弦值 sin B h PBθ==所以余弦值为10103cos =θ · ············12分 18 (本小题满分12分)解：（1）甲城市空气质量总体较好．…………………2分（2）甲城市在15天内空气质量类别为优或良的共有10天，任取1天，空气质量类别为优或良的概率为321510=， …………………3分乙城市在15天内空气质量类别为优或良的共有5天，任取1天，空气质量类别为优或良的概率为31155=， …………………4分在15天内任取1天，估计甲、乙两城市空气质量类别均为优或良的概率为923132=⨯．……………………6分 （3）X 的取值为2,1,0，…………………7分73)0(21521005===C C C X P ，2110)1(21511015===C C C X P ，212)0(21501025===C C C X P 所以X 的分布列为：…………………10分数学期望32212221101730=⨯+⨯+⨯=EX…………………12分19．（本小题满分13分）【解析】 (1)当1n =时时,由1121S a =-得113a =, 当 2≥n 时, 21n n S a =-①1121n n S a --=-②上面两式相减,得113n n a a -= 所以数列{}n a 是以首项为13,公比为13的等比数列,求得1()3n n a = ·········6分 (2) 11331111log 11log ()13n n n b a n ===+++，nc====1n T n =++=+ ············13分 20．（本小题满分13分）(Ⅰ) 由|PE |＋|PF |＝4＞|EF |及椭圆定义知，点P 的轨迹是以E ，F 为焦点，4为长轴长的椭圆．设P (x ，y )，则点P 的轨迹方程为24x＋y 2＝1． ………… 5分(Ⅱ) 设圆P 与圆F 的另一个公共点为T ，并设P (x 0，y 0)，Q (x 1，y 1)，T (x 2，y 2)，则由题意知，圆P 的方程为(x －x 0)2＋(y －y 0)2＝x 02＋y 02．又Q 为圆P 与圆F 的一个公共点，故22112222101000(5,()(),x y x x y y x y -+=-+-=+⎧⎨⎩ 所以(x 0x 1＋y 0 y 1－1＝0．同理(x 0x 2＋y 0 y 2－1＝0．因此直线QT 的方程为(x 0x ＋y 0y －1＝0．连接PF 交QT 于H ，则PF ⊥QT ．设|QH |＝d (d ＞0)，则在直角△QHF 中|FH |．又220014x y +=，故|FH |22==．在直角△QHF 中d1=．所以点Q 到直线PF 的距离为1． ………… 13分21. （本小题满分13分）(1)因为函数定义域为(0,)+∞，所以1ln 0ax x --≥即1ln x a x +≥，令1ln ()xg x x+=， 2ln ()0xg x x -'==得1x =(第21题图)因此max ()(1)1g x g ==，所以1a ≥ ………… 6分(2)由(1)知1a =时，1ln 0ax x --≥，即ln 1x x ≤-，则ln(1)x x +≤(当0x =时等号成立)，令1()x i N i *=∈，得11ln(1)i i+<，即1111,()i i i e e i i ++<<，取1,2,i n =，并累乘得23123234(1)(1)123!n n n n n n e n n ++⋅⋅=<1，所以(1)!n n n n e +<，(1)!n n n e n +<即e < ………… 13分。
2014年全国硕士研究生入学统一考试数学一试题及解析(完整精准版)一、选择题：1~8小题，每小题4分，共32分，下列每题给出四个选项中，只有一个选项符合题目要求的，请将所选项的字母填在答题纸指定位置上。
（1）下列曲线中有渐近线的是 （A ）sin y x x =+.(B)2sin y x x =+.(C)1sin y x x =+.(D)21sin y x x=+.【解析】1sin()11lim lim lim(1sin )1x x x x f x x a x x x x→∞→∞→∞+===+= 11lim[()]lim[sin ]limsin 0x x x b f x ax x x x x→∞→∞→∞=-=+-==∴y=x 是y=x +1sin x的斜渐近线【答案】C(2)设函数()f x 具有2阶导数，()()()()011g x f x f x =-+,则在区间[0，1]上（ ） (A)当0f x '≥（）时，()()f x g x ≥. (B)当0f x '≥（）时，()()f x g x ≤ (C)当0f x '≥（）时，()()f x g x ≥.(D)当0f '≥时，()()f x g x ≤【解析】当() 0f x "≥时，()f x 是凹函数而()g x 是连接()()0,0f 与()1,1f （）的直线段，如右图 故()() f x g x ≤ 【答案】D(3)设(),f x y是连续函数，则110(,)ydy f x y -=⎰⎰（A）11110(,)(,)x dx f x y dy dx f x y dy --+⎰⎰⎰.（B）1101(,)(,)xdx f x y dy dx f x y dy --+⎰⎰⎰⎰.（C ）112cos sin 02(cos ,sin )(cos ,sin ).d f r r dr d f r r dr ππθθπθθθθθθ++⎰⎰⎰⎰（D ）112cos sin 02(cos ,sin )(cos ,sin ).d f r r rdr d f r r rdr ππθθπθθθθθθ++⎰⎰⎰⎰【解析】积分区域如图 0≤y ≤1.1x y ≤≤-用极坐标表示，即：D 1:,012r πθπ≤≤≤≤ D 2: 10,02cos sin r πθθθ≤≤≤≤+【答案】D （4）若{}2211,(cos sin )(cos sin )mina b Rx a x b x dx x a x b x dxππππ--∈--=--⎰⎰，则11cos sin a x b x +=（A ）2sin x π.(B)2cos x .(C) 2sin x π. (D)2cos x π. 【解析】令2(,)(cos sin )Z a b x a x b x dx ππ-=--⎰2(cos sin )(cos )0(1)2(cos sin )(sin )0(2)a bZ x a x b x x dx Z x a x b x x dx ππππ--⎧'=---=⎪⎨'=---=⎪⎩⎰⎰由（1）得 202cos 0axdx π=⎰故10,0a a ==由（2）得 0120sin 22sin x xdx b b xdxππ===⎰⎰【答案】A(5)行列式00000000a b abc d c d= （A ）（ad-bc ）2（B ）-（ad-bc ）2。
2014安徽省省级示范高中名校高三联考数学（文科）参考答案（1）D 解析：()()122i 13i 55i.z z ⋅=-⋅+=+（2）A 解析：{}{}{}0123456,|3,4,5,6A B x x A B ==>∴⋂=，，，，，，.（3）B 解析：双曲线方程可化为221x y c c a b-=，即22142x y -=，∴离心率62e =. （4）D 解析：由指数、对数函数的图像可知1,0,01,.a b c a c b ><<<∴>> （5）C 解析：3322()()0.a b a b a ab b a b -=-++<⇔<（6）C 解析：由题意得011(0)201,(1)(1)212f b b f f -=-=⇒=∴=--=-+=. （7）A 解析：约束条件表示的是以()()()1,1,3,2,2,4A B C 为顶点的三角形区域，x y∴的最小值为12. （8）B 解析：()232f x ax bx c '=++，∴()2430b a c ∆=-=，故函数()f x 在R 上单调，∴()f x 有且只有一个零点.（9）A 解析：2111sin ,4442m m m m θ+==+≥∴π5π2π2π,66k k θ+≤≤+ππ2π36k θ+≤+ π2π,k Z k ≤+∈，故π11cos .62θ⎛⎫-≤+≤ ⎪⎝⎭（10）C 解析：由题意可知,B C 两点关于原点O 对称，∴24AB AC AO +==． （11）()0,2 解析：220x x ->，解得()0,2x ∈.（12）159 解析：程序运行如下：2419100;29119100a a =⨯+=<=⨯+=<；219139100;2391791002791159100,159.a a a =⨯+=<=⨯+=<=⨯+=>；输出（13）32 解析：圆心到直线的距离22=120231d AOB ==∴∠+，，AOB S ∆∴ 13=sin 22OA OB AOB ⋅⋅⋅∠=.（14）45 解析：记()()1,2n n S n +=如果最下层摆圆木n 根，最多能把圆木堆到()S n 根.把1000根圆木堆起来，若最下层摆圆木1n -根会剩下一些，摆n 根能摆完，则()()11000,S n S n -<≤即()()11100022n n n n -+<≤,∴()12000n n -<()1,n n ≤+由于44451980200045462070,⨯=<<⨯=∴45.n = （15）①②④ 解析：由PB ⊥AE ，PD ⊥AG AB AD =，，可得PB ,,PD PE PG ==//,BD//EG BD ∴∴平面AEFG ,①正确；由已知可得BC ⊥平面PAB ，CD ⊥平面PAD ，,AE BC AG CD ∴⊥⊥,又PB ⊥AE ，PD ⊥AG ，,,AE PC AG PC ∴⊥⊥∴PC ⊥平面AEFG ,②正确；由②可知EF PC EF ⊥∴，与BC 必相交，假设//EF 平面PAD ，由//BC 平面PAD 可得平面PAD //平面PBC ，显然矛盾，③错误；由②可知1,2O A O B O C O D O E O F O G A C =======∴点,,,,,,A B CD E F G 在同一球面上,④正确；连接AF ，取AF 的中点M ，连接OM ，则//,OM PC OM AEFG ∴⊥平面,由已知可得2663,2363AE AF EF OM ==∴==∴，，，四棱锥O A E -的体积1,318A EE F O MV ⋅⋅==⑤错误.（16）解析：（Ⅰ）由已知及正弦定理可得222222221,2,a b ab a b c ab c c ++=+-=- 22cos ,22ab C ab -∴==-3π4C ∴=.（6分） （Ⅱ）由正弦定理得sin 1sin 2a C A c ==，又π02A <<，π6A ∴=， 故3ππtan tan46tan tan()2 3.3ππ1tan tan46B AC +=-+=-=--⋅（12分） （17）解析：（Ⅰ）面试分数在[)50,60内的频数为2，由频率分布直方图可以看出，分数在[)90,100内同样有2 人，由2100.01n=⨯，得20n =.（2分）由茎叶图可知面试成绩的中位数为7476=752+.（4分） 分数在[)80,90内的人数为()2025724-+++=.（6分）（Ⅱ）将[)80,90内的4人编号为a b c d ,,,,[)90,100内的2人编号为A B ,, 在[)80,100内任取两人的基本事件为：,,ab ac ad aA aB ,,,bc bd ,,,bA bB ,cd cA cB dA dB AB ,,,,,,共15个，其中恰好有一人分数在[)90,100内的基本事件为：,aA aB ,,bA bB ,,cA cB dA ,,dB ,共8个,∴恰好有一人分数在[)90,100内的概率为815.（12分） （18）解析：（Ⅰ)连接AC,BD 交于点O ，连接OF ，则OF 12PA ,又//,//,DE PA DE OF ∴////,EF ABCD ODEF ABCD OD EF OD ⋂=∴平面，平面平面，∴ODEF 为平行四边形，1,2DE PA ∴=又4,CD DE 3 1.PA CD DE +=+=∴=，（6分） （Ⅱ）//EF BD BD PAC EF PAC ⊥∴⊥，平面，平面,过点A 作AG PC ⊥，垂足为G ，则AG ⊥平面PCE ，22226=348AG ⨯=+，即点A 到平面PCE 的距离为263.（12分） （亦可用体积相等法求解） （19）解析：（Ⅰ）()1a x af x x x-'=-=，()f x 的定义域为()0,+∞， 令()0f x '=，得x a =，此时()f x ，()f x '随x 的变化情况如下表：∴()f x 的单调递减区间为()0,a ，单调递增区间为(),a +∞.(6分) （Ⅱ）由（Ⅰ）及题意知()()min 1ln 0f x f a a a a ==--≥， 令()1ln g a a a a =--，可得()ln g a a '=-， ∴()g a 在()0,1上单调递增，在()1,+∞上单调递减，∴()()max 10g a g ==，故使1ln 0a a a --≥成立的解只有1a =， ∴实数a 的取值集合为{}1.（13分）x ()0,aa(),a +∞()f x ' -+()f x↓ 极小值↑（20）解析：（Ⅰ）由已知得220n n n a a S +-=,①当2n ≥时,021121=-+---n n n S a a ,②①-②得11111()()20()(1)0n n n n n n n n n n n a a a a a a a a a a a ------++--=+--=，即， 数列{}n a 的各项都是正数，11n n a a -∴-=,当1n =时，021121=-+a a a ，11,1(1)n a a n n ∴=∴=+-=.（6分）（Ⅱ）由（Ⅰ）及已知得01111112222n n T n -⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，①两边同乘以12得121111122222nn T n ⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，②①-②得111112222n n n n T -=+++-, 11124(1)44222n n n n n n T --+=--=-<,又1132144 =0222n n n n n n n n T T +-+++-=--+>,∴11n T T ≥=,故存在正整数1m =满足要求.（13分）（21）解析：（Ⅰ）由已知得222261412a b a b ⎧⎪⎪+=⎨⎪-=⎪⎩，解得2242a b ⎧=⎪⎨=⎪⎩，∴椭圆C 的方程为.12422=+y x （4分） （Ⅱ）设1122(,),(,),P x y Q x y 由椭圆C 的方程为22142x y +=知 2222111112||(2)(2)2222x PF x y x x =++=++-=+，同理222|Q |2,||2.22F x MF =+=+ .2),(224)222(2|,|||||22121=+∴++=+∴+=x x x x QF PF MF ①当221112222224,24x y x x x y ⎧+=⎪≠⎨+=⎪⎩时由，得22221212()2()0x x y y -+-=， 由12x x ≠可得12y y ≠±,从而有.2121212121y y x x x x y y ++⋅-=--设线段PQ 的中点为(1,)0,N n n ≠（）则121212PQ y y k x x n-==--， 得线段PQ 的中垂线方程为2(1)y n n x -=-,(21)0,x n y ∴--=该直线恒过一定点1(,0).2②当126666,(1,),(1,)(1,),(1,)2222x x P Q Q P =--时或, 线段PQ 的中垂线是x 轴，也过点1(,0)2.∴线段PQ 的垂直平分线经过一个定点1(,0)2.（13分）。
