大学物理-第二章连续体的运动
- 格式:ppt
- 大小:1.77 MB
- 文档页数:48
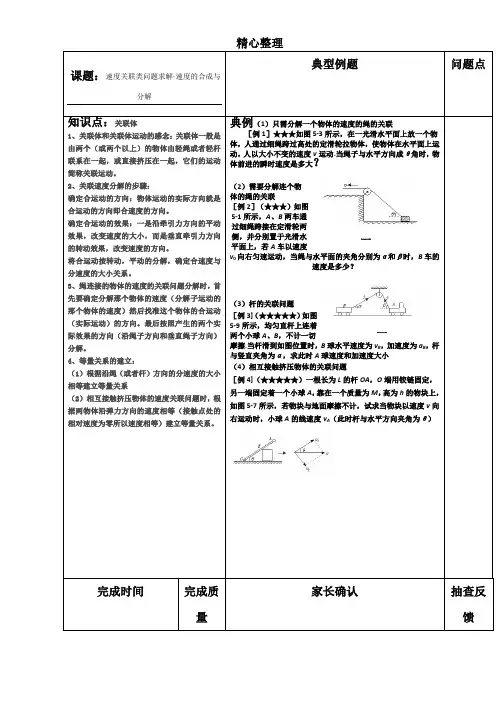
精心整理课题:速度关联类问题求解·速度的合成与分解典型例题问题点知识点:关联体1、关联体和关联体运动的感念:关联体一般是由两个(或两个以上)的物体由轻绳或者轻杆联系在一起,或直接挤压在一起,它们的运动简称关联运动。
2、关联速度分解的步骤:确定合运动的方向:物体运动的实际方向就是合运动的方向即合速度的方向。
确定合运动的效果:一是沿牵引力方向的平动效果,改变速度的大小,而是垂直牵引力方向的转动效果,改变速度的方向。
将合运动按转动,平动的分解,确定合速度与分速度的大小关系。
3、绳连接的物体的速度的关联问题分解时,首先要确定分解那个物体的速度(分解子运动的那个物体的速度)然后找准这个物体的合运动(实际运动)的方向。
最后按照产生的两个实际效果的方向(沿绳子方向和垂直绳子方向)分解。
4、等量关系的建立:(1)根据沿绳(或者杆)方向的分速度的大小相等建立等量关系(2)相互接触挤压物体的速度关联问题时,根据两物体沿弹力方向的速度相等(接触点处的相对速度为零所以速度相等)建立等量关系。
典例(1)只需分解一个物体的速度的绳的关联[例1]★★★如图5-3所示,在一光滑水平面上放一个物体,人通过细绳跨过高处的定滑轮拉物体,使物体在水平面上运动,人以大小不变的速度v运动.当绳子与水平方向成θ角时,物体前进的瞬时速度是多大?(2)需要分解连个物体的绳的关联[例2](★★★)如图5-1所示,A、B两车通过细绳跨接在定滑轮两侧,并分别置于光滑水平面上,若A车以速度v0向右匀速运动,当绳与水平面的夹角分别为α和β时,B车的速度是多少?(3)杆的关联问题[例3](★★★★★)如图5-9所示,均匀直杆上连着两个小球A、B,不计一切摩擦.当杆滑到如图位置时,B球水平速度为v B,加速度为a B,杆与竖直夹角为α,求此时A球速度和加速度大小(4)相互接触挤压物体的关联问题[例4](★★★★★)一根长为L的杆OA,O端用铰链固定,另一端固定着一个小球A,靠在一个质量为M,高为h的物块上,如图5-7所示,若物块与地面摩擦不计,试求当物块以速度v向右运动时,小球A的线速度v A(此时杆与水平方向夹角为θ)完成时间完成质量家长确认抽查反馈图图精心整理。


第二部分 连续介质力学第一章 连续介质的运动学物质是由原子和分子组成的。
因此,物质是不连续的。
但在日常生活中却有许多有关物质行为的外观现象,它们可以用不考虑物质分子结构的宏观理论来加以描述和预示。
例如,钢杆在已知力的作用下的伸长量,管道中水流的排出速度和物质在空气中运动所受到的阻力等等。
连续介质力学把物质看作是无限可分的,因此我们需要将物质的无限小体积看作是连续介质中的物质点或“粒子”。
1.1 连续介质的运动假设一个物体在某一瞬时(t t =0)占有物理空间V 0(充满物质的某一空间区域)。
在该瞬时物体中任一物质点P 的几何位置可以用由某一固定点O 引出的位置矢量X 来描述,而该物质点P 在任意瞬时t 的位置用位置矢量x 来表示(图1.1)。
因此,任何一个物质点的运动路线可由下列形式的方程描述:()t X x x ,= (1.11) 上式表示在初始0时刻占据位置X 的的物质在时刻t 的位置。
我们可以把方程看成是从空间区域V 0到V 的关于X 和x 的一一对应的连续变换。
它描述物体中任一物质的瞬时位置。
我们把对组成物质的全体物质点位置的完全刻画称为物体的构形(Configuration)。
另一方面,物体的运动也可由下列形式的方程描述:()t x X X ,= (1.12) 它表示在时刻t ,通过空间x 处的物质原来的初始位置。
如果在时刻t ,处于整个空间中每一物质点的原始位置都被给出,那么物体在t 时刻的构形也被完全地描述了。
若方程1.11和1.12描述同一运动过程,并且雅可比行列式 0det ≠⎥⎥⎦⎤⎢⎢⎣⎡=j i X x J ∂∂ (1.13)则式1.11和式1.12为互逆变换,且唯一。
在直角坐标系基矢量下()321,,e e e ,1.11式可以表示成x x e x e x e =++112233 (1.14) 于是方程具有下列分量形式: ()t X X X x x ,,,32111= ()t X X X x x ,,,32122=()t X X X x x ,,,32133= (1.15) 写成指标记法形式则为()t X X X x x i i ,,,321= (1.16) 同样地,方程1.12的指标记法形式为()t x x x X X i i ,,,321= (1.17)方程中X 是用来确定物体中的不同物质的,称之为物质坐标;而方程中的x 是用来确定物理空间中物体内各个物质点的空间位置的,因此我们称之为物质的空间坐标。





连续体系●系统具有连续分布的质量和弹性●物体内材料均匀,各向同性,弹性极限内服从胡克定律●弹性体具有无限多的自由度⏹需要无限多的坐标指定弹性体中任一点的位置●弹性体自由振动可以看成主振型或者正则振型的叠加●对于正则振型的振动,每个颗粒都做简谐振动⏹其频率是相应频率方程的根⏹各颗粒同时经过各自的平衡位置⏹如果物体的运动起始时的弹性曲线精确与每个主振型一致,物体将仅作主振动⏹爆炸或者外力的突然移除导致的弹性曲线,通常与主振动不一致,因而会激起所有振型的振动●在很多情况下,可以通过适当的初始条件激起某个特定的主振型●对于连续质量分布的系统的受迫振动,通过振型叠加法,可以使其转变为有限自由度的系统进行分析●常常把约束作为结构的附加支承来处理⏹会改变系统的主振型●用于表征系统变形的振型不需要一定是正交的●存在使用非正交函数的系统合成⏹例如在进行颤振计算时,为了避免质量变化引起正交振型改变时导致气动力的重新计算,可采用非正交振型,在每次计算中,保持振型不变,而重新计算非对角形式的广义质量矩阵弦的振动●一个柔软的弦,单位长度的质量为,在拉力作用下被张紧●假定其横向挠度很小,挠度引起的张力变化也很小,可以忽略不计●考虑单元长度为的一段弦的受力●挠度和斜率均很小●向的运动方程为●弦的斜率⏹波的扩展速度●一般解可以表示成如下的形式⏹和为任意函数●不管函数的类型如何,对变量微分将得到●如果做变量代换●注意到●简化后●积分两次⏹分量波以速度沿着轴方向移动⏹分量表示波以速度沿着轴方向移动⏹看成是波扩展的速度.●这一方法称为行波法10分离变量法●假定解具有分离变量的形式●代入微分方程后可得●方程左边各项与无关,方程右边各项与无关,因此两边必须是常数●令这个常数为, 得到两个常微分方程●其通解为⏹其中的待定常数, , , 由边界条件和初始条件确定●例题两端固定的张紧的弦,长度为 边界条件为●由●由为波长; 为振动频率的每个值代表一个主振动模态 固有频率为●振型为如下的正弦函数●由任意方式激起的更一般情况的自由振动, 解包括多个振动模态, 位移方程可以写为●应用初始条件and, 可以计算出和●如果把弦拉成任意形状后释放,初始条件可以表示为●每个方程都乘以并从到积分, 方程右边各项除外均为零。
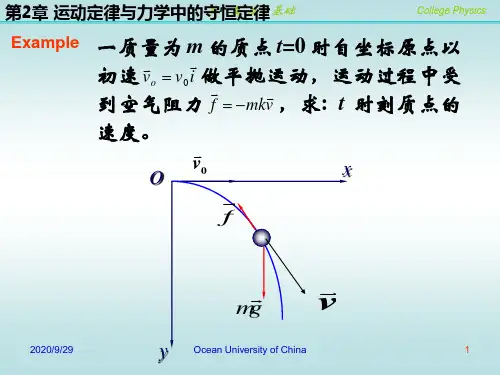


补充:刚体绕固定转轴转动时角加速度与力矩关系的数学表达式为=M J β;易1、转动惯量为1002.kg m 的刚体以角加速度为52.rad s -绕定轴转动,则刚体所受的合外力矩为500()N m ⋅ N.m 。
中2、一根匀质的细棒,可绕右端o 轴在竖直平内转动。
设它在水平位置上所受重力矩为M ,则当此棒被切去三分之二只剩右边的三分之一时,所受重力矩变为 9M。
易3、在刚体作定轴转动时,公式t t βωω+=0成立的条件是 β=恒量 。
中4、一飞轮以300rad1min -⋅的转速旋转,转动惯量为5kg.m2,现加一恒定的制动力矩,使飞轮在20s 内停止转动,则该恒定制动力矩的大小为 2.5(.)N m π .易5、如图所示,质量为M 、半径为R 的均匀圆盘对通过它的边缘端点A 且垂直于盘面的轴的转动惯量A J =232MR 。
难6、如图示一长为L ,质量为M 的均匀细杆,两端分别固定有质量都为m 的小球。
当转轴垂直通过杆的一端时,其转动惯量为 2213mL ML + ;当转轴通过垂直杆的1/3(1/2;1/4)处时,转动惯量为225199mL ML + 。
易7、瞬时平动刚体上各点速度大小相等,但方向可以 相同 (填不同或相同)。
易8、刚体的转动惯量与刚体的形状、大小、质量分布有关、与转轴位置 有关 (填易9、所谓理想流体是指 绝对不可压缩和 完全没有粘滞性 的流体,并且在同一流管内遵循 连续性 原理。
中10、一水平流管,满足定常流动时,流速大处流线分布较密,压强较 小 ; 流线分布较疏时,压强较 大 ;若此两处半径比为1∶2,则其流速比为 4:1易11、已知消防队员使用的喷水龙头入水口的截面直径是-26.410m ,出水口的截面直径是-22.510m ,若入水的速度是14.0m S ,则射出水的速度为 126()m s -⋅易12、一长l 为的均匀细棒可绕通过其端、且与棒垂直的水平o 自由转动,其转动慣量为231ml J =,若将棒拉到水平位置,然后由静止释放,此时棒的角加速度大小为 32gl。