ABAQUS有限元分析方法

一、有限单元法的基本原理有限单元法（The Finite Element Method）简称有限元（FEM），它是利用电子计算机进行的一种数值分析方法。

它在工程技术领域中的应用十分广泛，几乎所有的弹塑性结构静力学和动力学问题都可用它求得满意的数值结果。

有限元方法的基本思路是：化整为零，积零为整。

即应用有限元法求解任意连续体时，应把连续的求解区域分割成有限个单元，并在每个单元上指定有限个结点，假设一个简单的函数（称插值函数）近似地表示其位移分布规律，再利用弹塑性理论中的变分原理或其他方法，建立单元结点的力和位移之间的力学特性关系，得到一组以结点位移为未知量的代数方程组，从而求解结点的位移分量. 进而利用插值函数确定单元集合体上的场函数。

由位移求出应变, 由应变求出应力二、ABAQUS有限元分析过程有限元分析过程可以分为以下几个阶段1.建模阶段: 建模阶段是根据结构实际形状和实际工况条件建立有限元分析的计算模型――有限元模型，从而为有限元数值计算提供必要的输入数据。

有限元建模的中心任务是结构离散，即划分网格。

但是还是要处理许多与之相关的工作：如结构形式处理、集合模型建立、单元特性定义、单元质量检查、编号顺序以及模型边界条件的定义等。

2.计算阶段:计算阶段的任务是完成有限元方法有关的数值计算。

由于这一步运算量非常大，所以这部分工作由有限元分析软件控制并在计算机上自动完成3.后处理阶段: 它的任务是对计算输出的结果惊醒必要的处理，并按一定方式显示或打印出来，以便对结构性能的好坏或设计的合理性进行评估，并作为相应的改进或优化，这是惊醒结构有限元分析的目的所在。

下列的功能模块在ABAQUS/CAE操作整个过程中常常见到，这个表简明地描述了建立模型过程中要调用的每个功能模块。

“Part（部件）用户在Part模块里生成单个部件，可以直接在ABAQUS/CAE环境下用图形工具生成部件的几何形状，也可以从其它的图形软件输入部件。

科学技术创新2021.10基于ABAQUS 软件的静压钢板桩有限元模拟分析李宇航（广东工业大学，广东广州510006）1概述桩基础是一种对土质环境适应性较强的建筑基础，其具有久远的历史及较高的承载力，被广泛地应用于高层、桥梁、码头等建筑物中。

近年来，随着国家经济的高速发展及城镇化步伐的加快，极大促进了钢板桩在我国的发展和应用。

钢板桩作为一种现代基础与地下工程领域的重要工程建设的施工材料，可满足传统水利、土木道路交通工程、环境污染整治及突发性灾害控制等众多工程领域的施工需求[1]。

近年来，随着静压桩技术的广泛应用，静压钢板桩这一施工优势逐渐显现出来。

目前，众多学者对静压桩的沉桩机理进行了数值模拟研究，如张吉坤等[2]用ABAQUS 软件建立了静压桩连续贯入土体的有限元模型，探讨了沉桩过程中桩周土体的应力与应变分布特征，得到了贯入阻力随深度变化的规律。

郝友超[3]利用ABAQUS 数值模拟软件，对沉桩过程中压桩力、桩端阻力以及桩侧摩阻力随沉桩深度的变化进行了分析，实现了模型桩在砂土内连续贯入的数值仿真。

辛翀[4]利用ABAQUS 软件对某工程静压桩进行了数值分析，并将软件处理的结果与实测结果进行了比较。

牛永昌[5]借助静压桩的沉桩阻力及承载力时效性的现场实验数据，用ABAQUS 有限元分析软件对静压桩的沉桩阻力、桩端阻力等进行了系统分析研究。

本文结合实际情况，在ABAQUS 平台上，采用Coupled Eulerian-Lagrangian (CEL)方法，对钢板桩的沉桩过程进行了模拟分析，研究了钢板桩在沉桩过程中沉桩阻力随深度的变化规律，同时，研究了选用不同本构模型对钢板桩沉桩阻力的影响，研究成果对于静压钢板桩的实际施工具有理论指导意义。

2有限元模型的建立及参数设置本文在ABAQUS 平台上，采用CEL 法对钢板桩单桩沉桩的过程进行模拟分析。

模拟采用总应力法；模拟过程中假定土体为均质连续的弹塑性土体，桩为刚性体；考虑土体初始应力的影响。

有限元分析课程论文课程名称：有限元分析论文题目：ujoint有限元分析学生班级；学生姓名：任课教师：学位类别：评分标准及分值选题与参阅资料（分值）论文内容（分值）论文表述（分值）创新性（分值）评分论文评语：总评分评阅教师: 评阅时间年月日注：此表为每个学生的论文封面，请任课教师填写分项分值基于abaqus的ujoint有限元分析摘要：万向传动装置在汽车中起到了传递扭矩的关键作用,在abaqus中导入ujoint实体模型，之后对其进行坐标系建立，wire 建立，以及各部件之间的连接关系的建立，最后对该模型施加边界条件，令其运动。

关键词：abaqus、有限元、ujoint一问题的描述对导入的ujoint在所有步骤完成后，施加力：在stepinitial：均设为0；step SPIN：doundary1：限制除UR2的所有，且把UR2值设为：pi。

在boundary2 中，限制UR1和UR3自由度。

二在abaqus中导入ujoint实体模型启动abaqus CAE，在文件下拉菜单中选择：import ，选择最终文件位置or 输入ws_connector_ujoint.py.inp打开文件ujoint。

（如下图所示）2.1 创建坐标系单机操作界面中的tool，从下拉菜单中选择datum，再出来的窗口中选择coordinate，3points。

首先选择origin，在选择x正方向，Y正方向、z正方向。

创建完成。

2.2创建VERT和CROSS之间的2坐标系。

根据 2.1所述操作步骤创建坐标系V-C 和V-G （VERT和GROUND）。

Notice：1、创建过程中为了清晰分辨，可将IN的suppress，创建完成后再将其resume。

其他同样2、在V-C和I-C中，x轴与cross转动所绕轴平行。

根据2.1所属步骤创建I-C 和I-G. 结果如图；2.3 定义connector geometry1. 2.3.1 创建disjoint型wire在选项中选择interaction，在所出现窗口中点击Create Wire Feature tool.，在所出现的窗口中选择Disjointwires，单机添加要成wire的点。

ABAQUS钢筋混凝土有限元分析钢筋混凝土作为一种常见的建筑材料，在建筑、交通、水利等领域得到了广泛应用。

然而，钢筋混凝土结构在服役期间会受到多种复杂荷载的作用，导致结构性能退化甚至破坏。

因此，对钢筋混凝土结构进行精确的分析和模拟至关重要。

ABAQUS是一款强大的工程仿真软件，能够模拟各种材料和结构的力学行为。

本文将介绍如何使用ABAQUS 对钢筋混凝土进行有限元分析。

ABAQUS是一款专业的有限元分析软件，它提供了丰富的材料模型库和边界条件设置功能，可以模拟各种复杂结构的力学行为。

ABAQUS具有强大的前后处理功能，用户可以通过直观的界面进行模型构建、材料属性设置、边界条件施加等操作。

同时，ABAQUS还提供了强大的数据分析和可视化工具，方便用户对模拟结果进行详细分析。

钢筋混凝土是由钢筋和混凝土两种材料组成的复合材料。

混凝土是一种抗压强度高、抗拉强度低的材料，而钢筋具有较高的抗拉强度和塑性。

将钢筋嵌入混凝土中，可以提高结构的抗拉强度、抗压强度和韧性。

钢筋混凝土还具有较好的耐久性和防火性能。

在有限元分析中，需要对钢筋混凝土的力学性能进行适当简化。

通常假定混凝土为各向同性材料，钢筋为弹塑性材料。

同时，还应考虑混凝土的裂缝、损伤以及钢筋与混凝土之间的粘结和滑移等因素。

在ABAQUS中，可以对钢筋混凝土结构进行详细的有限元分析。

需要建立合适的计算模型，包括几何模型、材料属性、边界条件和荷载等。

模型建立完成后，可以通过ABAQUS的求解器进行计算，得到各节点位移、应力、应变等结果。

通过对计算结果的分析，可以评价结构的性能和安全性。

例如，可以通过应力和应变分布情况，分析结构的整体和局部稳定性、裂缝分布及扩展等。

还可以观察钢筋与混凝土之间的粘结性能以及评估结构的耐久性。

本文介绍了如何使用ABAQUS对钢筋混凝土进行有限元分析。

通过建立合适的计算模型，设置材料属性和边界条件，以及进行求解计算，可以得到结构的详细应力、应变和位移分布情况。

定义ABAQUS分析步及输出ABAQUS是一种常用的有限元分析软件，用于进行结构和材料的非线性有限元分析。

在ABAQUS中，分析步是指模拟结构在时间上的演化过程，输出则是指对分析结果的检测和处理。

一、ABAQUS的分析步ABAQUS中的分析步用于描述模型的运动和应力应变状态的演化情况，通过定义不同的分析步可以模拟不同的物理过程和加载条件。

1.静力分析步：这是最基础的分析步类型，用于模拟结构在静力加载下的行为。

静力分析步中的加载可以是恒定的或者是按照一定的时间函数变化的。

在静力分析步中，结构的应力应变状态被认为是平衡的。

2.动力分析步：该步骤用于模拟结构在动力加载下的行为。

动力分析步中的加载可以是周期性的、脉冲的、随机的等等。

在动力分析步中，结构的应力应变状态随时间而变化。

3.热分析步：用于模拟材料在不同温度条件下的热行为。

热分析步包括传热、热膨胀和热应力等。

4.接触分析步：用于模拟接触问题，例如刚性接触、摩擦接触等。

接触分析步中，通过定义接触边界条件和接触特性来模拟接触行为。

5.融合分析步：用于模拟结构在拉伸、压缩、剪切等加载下的塑性和破裂行为。

融合分析步通常包括弹塑性材料本构关系、破裂准则等。

6.稳态分析步：用于模拟结构在稳态加载下的行为，例如结构在恒定温度或恒定力加载下的应力应变状态。

除了以上常见的分析步类型，ABAQUS还提供了许多其他类型的分析步，例如电磁场分析、疲劳分析、生物力学分析等，以适应不同领域的应用需求。

二、ABAQUS的输出在分析过程中，ABAQUS会输出大量的结果数据和信息以帮助用户了解模型的应力应变状态和物理行为。

ABAQUS的输出结果可以分为以下几类：1.节点和单元数据：ABAQUS会输出模型中每个节点和单元的位移、速度、应力、应变等数据，以及其他相关属性如质量、体积等。

这些数据有助于确定结构的局部和整体行为，以及结构的应力集中区域。

2.特征数据：ABAQUS还提供一些用于描述模型行为的特征数据，如结构的自然频率、振型、模态参与因子等。

ABAQUS有限元分析方法有限元分析是一种将连续问题离散化成有限数量的元素，通过求解这些离散化的元素的行为，来推断整个问题的行为的数值分析方法。

ABAQUS就是一种基于有限元方法的求解器，它使用了计算机模拟技术，可以求解各种工程问题，如结构力学、热力学、流体力学等。

建模是有限元分析的第一步，ABAQUS提供了多种建模技术和工具来帮助用户创建复杂的几何模型。

用户可以使用ABAQUS提供的几何建模工具来创建三维模型，也可以导入其他计算机辅助设计（CAD）软件生成的模型。

在建模过程中，用户还可以定义材料属性、加载条件和约束等。

一旦建立了几何模型，用户就可以定义有限元网格。

有限元网格是将模型离散化为有限数量的单元的过程。

ABAQUS提供了多种类型的单元，如线性和非线性、静力学和动力学等。

用户可以根据具体的问题选择适当的单元类型。

通常，使用更精细的网格可以提高解的精度，但也会增加计算时间和内存需求。

在模型离散化后，用户需要定义材料特性和加载条件。

ABAQUS支持多种材料模型，如线性弹性、非线性材料、塑性材料等。

用户可以根据材料的真实性质选择适当的材料模型，并提供相关参数。

加载条件是指施加到模型上的外部载荷或约束。

用户可以定义各种加载条件，如受力、温度、位移约束等。

建立好模型后，用户需要选择适当的求解方法。

ABAQUS提供了多种求解方法，如直接方法、迭代方法、稳定方法等。

用户可以根据问题的特点选择适合的求解方法，并提供求解的控制参数。

完成求解后，用户可以对结果进行后处理。

ABAQUS提供了丰富的后处理工具，可以可视化模型的应力、应变、位移等结果。

用户可以进一步分析和评估模型的响应。

在使用ABAQUS进行有限元分析时，一些常见的技巧和注意事项包括：-使用合适的网格：细化网格可以提高解的精度，但需要更多的计算资源。

-使用合适的材料模型：根据材料的真实性质选择适当的材料模型，并提供正确的参数。

-检查模型：在求解之前，检查模型的几何和网格是否正确，以及加载条件是否合理。

基于ABAQUS的有限元分析过程有限元分析（finite element analysis，FEA）是一种基于数值计算方法的工程分析技术，通过将连续物理问题离散化为有限个单元，利用有限元方法对每个单元进行数值计算，最终得到整个结构的力学行为。

ABAQUS是一种强大的有限元分析软件，广泛应用于工程领域。

1.建立几何模型：几何模型的建立需要根据具体问题的要求，可以通过ABAQUS提供的预处理软件模块CAE来进行建模。

在CAE中，可以使用CAD文件导入几何模型，也可以通过绘制线条、曲线和体素等几何元素进行建模。

2.定义材料特性：材料的力学性质是有限元分析的基础，需要定义材料的弹性模量、泊松比、屈服强度等力学参数。

在ABAQUS中，可以选择不同的材料模型：线弹性、塑性、弹塑性等。

3.网格生成：网格生成是离散化的过程，将几何模型分割成有限个小单元。

ABAQUS提供了多种网格生成算法和工具，可以根据问题的要求进行网格划分。

4.加载和约束定义：在有限元分析中，需要定义结构的加载和约束条件。

加载条件可以是施加在结构上的力、压力、温度等，约束条件可以是固定支撑、约束位移等。

ABAQUS提供了丰富的加载和约束选项，可以满足各种复杂问题的需求。

5.定义分析类型和求解器：有限元分析可以包括静力学、动力学、热传导、流体力学等不同类型的分析。

ABAQUS提供了各种分析类型和求解器，可以选择适合问题的分析类型和求解器进行求解。

6.运行分析并后处理：在上述步骤都完成后，可以运行分析，并对分析结果进行后处理。

ABAQUS提供了丰富的后处理工具，可以对结果进行可视化显示、应力、应变等字段分析和报表生成。

7.优化设计：在得到初步分析结果后，可以根据分析结果进行结构的优化设计。

ABAQUS提供了一些优化算法和工具，可以帮助用户快速得到优化设计结果。

总结起来，基于ABAQUS的有限元分析过程包括建立几何模型、定义材料特性、网格生成、加载和约束定义、定义分析类型和求解器、运行分析和后处理等步骤。

abaqus有限元动力学标准算例
ABQUS有限元动力学标准算例有很多，以下是其中几个常见的：
1. Cantilever Beam（悬臂梁）：这个算例用于模拟一个悬臂梁
在受到外部荷载作用时的振动响应。

它可以用来研究悬臂梁的固有频率和模态形态。

2. Free Vibration of a Mass-Spring System（质量弹簧系统自由
振动）：这个算例模拟了一个质量和弹簧相连接的系统在没有外部激励下的自由振动情况。

它可以用来研究系统的固有频率和振动模态。

3. Transient Analysis of a Simply Supported Beam（简支梁的瞬
态分析）：这个算例模拟了一个简支梁在受到一定冲击荷载后的动态响应。

它可以用来研究梁在冲击荷载下的振动行为。

4. Modal Analysis of a Plate（平板的模态分析）：这个算例模
拟了一个平板结构的模态响应。

它可以用来研究平板的固有频率和振动模态。

这些算例都可以在ABQUS官方网站上找到详细的教程和步骤。

此外，ABQUS还提供了更多的动力学分析算例，涵盖了不同
类型的结构和加载条件。

可以根据具体的需求选择适合的算例进行研究和分析。

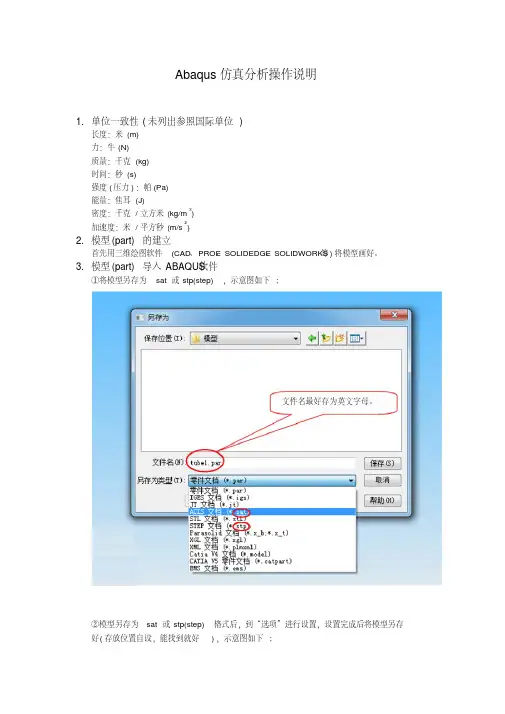
abaqus 教程Abaqus是一款常用的有限元分析软件，本教程将介绍如何使用Abaqus进行有限元分析。

首先，我们需要在Abaqus中创建一个新的分析模型。

进入Abaqus软件后，点击"File"，然后选择"New"，再选择"Model"，新建一个分析模型。

接下来，我们需要定义模型的几何形状。

点击"Part"，然后选择"Create"，再选择"Solid"，输入合适的几何形状参数，如长宽高等。

创建几何形状后，可以进行必要的修整和修剪操作，以满足实际需要。

完成几何形状定义后，我们需要定义模型的材料属性。

点击"Material"，然后选择"Create"，再选择适当的材料类型，如金属、塑料等。

在材料定义中，需要输入与材料性质相关的参数，如弹性模量、泊松比等。

根据实际情况输入相应的参数值。

接下来，我们需要定义模型的边界条件。

点击"Assembly"，然后选择"Create"，再选择"Instance"，将模型实例化。

然后，点击"Step"，选择"Create"，再选择"Static"，定义静态分析的步骤。

在步骤定义中，需要输入与分析相关的参数，如加载条件、约束条件等。

完成步骤定义后，我们可以进行模型的网格划分。

点击"Mesh"，选择"Create"，再选择适当的网格划分方法，如自动划分、手动划分等。

进行网格划分时，需要根据几何形状和分析要求设置适当的网格密度和尺寸。

完成网格划分后，我们可以进行模型的求解计算。

点击"Job"，选择"Create"，再选择"Standard"，创建一个求解任务。

ABAQUS有限元分析方法ABAQUS是一种广泛使用的有限元分析软件，它可以用于计算和模拟复杂的实际工程问题。

ABAQUS能够解决结构力学、热力学、电磁学、流体力学、多物理场等各类问题，具备强大的建模和分析能力。

本文将介绍ABAQUS的有限元分析方法，包括其基本原理、建模流程、边界条件的设置以及结果分析等内容。

有限元分析方法是一种通过将连续物体离散为有限个小单元来近似求解连续介质中的物理场分布和结构行为的方法。

它基于连续介质力学、力学平衡方程和边界条件等理论，通过在每个单元内进行离散近似，将大问题分解为由离散单元组成的小问题，然后通过求解这些小问题得到整个问题的近似解。

ABAQUS的建模流程主要包括几何建模、边界条件的设置、网格划分和材料定义等步骤。

几何建模是指在ABAQUS软件中创建所需分析的几何形状，可以通过绘制直线、圆弧、曲线或导入CAD模型等方式进行。

边界条件设置则是指为模型的一些面或点施加边界条件，包括固定支撑、施加力、约束等。

网格划分是指将模型中的连续介质离散化为有限个小单元，ABAQUS可以进行自动网格划分或手动划分网格。

材料定义是指为模型中的每个单元指定材料属性，例如弹性模量、泊松比、密度等。

在边界条件设置和材料定义完成后，可以对模型进行加载和求解。

首先，需要指定施加在模型上的加载条件，例如力、温度、电场等。

然后，在分析控制命令下选择适当的解析方法和参数，启动求解器对模型进行计算。

ABAQUS的求解器可以是显式求解器或隐式求解器，根据具体的问题选择合适的求解器类型。

计算完成后，可以对结果进行后处理，包括生成应力、应变分布图、振动模态分析、疲劳分析等。

在进行有限元分析时，需要注意选择合适的单元类型和网格密度。

ABAQUS提供了多种类型的单元，例如线性单元、三角形单元、四边形单元、六面体单元等，根据几何形状和物理场的特点选择合适的单元类型。

网格密度决定了分析结果的精度和计算时间，通常需要进行网格收敛性分析，即逐步增加网格密度，直到结果在精度和计算时间之间达到平衡。

ABAQUS有限元分析方法有限元分析是一种通过将结构分割成许多小的有限元单元，并将公式应用于每个单元来近似求解结构响应的方法。

ABAQUS将这种方法应用于现实世界的问题，提供了一个功能强大的平台来进行各种类型的分析，例如线性和非线性静态和动态分析、热力学分析、耦合场分析等。

要进行有限元分析，首先需要建立一个准确的模型。

ABAQUS提供了多种建模工具，例如部件建模、装配件和总装建模。

在进行建模时，需要选择适当的材料属性和边界条件。

这些参数将影响最终的分析结果的准确性。

一旦建立了模型，就可以进行有限元网格划分。

ABAQUS提供的网格生成工具可以自动划分结构，并根据用户需求进行网格优化。

划分的有限元单元数量越多，模型将越准确，但计算时间也将增加。

完成网格划分后，可以进行求解。

ABAQUS使用了迭代解算器来计算结构的响应。

迭代解算器根据预设的收敛准则进行迭代，直至达到收敛性。

ABAQUS还提供了多种线性算法和非线性求解器，以应对不同类型的问题。

一旦求解完成，可以进行后处理。

ABAQUS提供了丰富的后处理工具，包括生成应力和应变云图、振动模态分析、动态响应分析、瞬态分析等。

这些工具帮助分析师更好地理解结构的行为。

需要注意的是，在使用ABAQUS进行有限元分析时，需要对软件进行适当的验证和验证。

这可以通过与实验数据进行比较来确定模型的准确性。

此外，还应考虑材料的非线性行为、接触和接触分析等现实世界中的复杂问题。

总而言之，ABAQUS是一种功能强大的有限元分析软件，通过准确的建模、网格划分、求解和后处理工具，可以提供准确的结构响应分析。

然而，分析师需要具备一定的专业知识和经验来正确使用该软件，并对分析结果进行适当的解释和验证。

石亦平《ABAQUS有限元分析实例详解》之读后小结第九章动态分析实例[95] (pp280) ABAQUS包括两大类方法：振型叠加法（modal superposition procedure）：用于求解线性动态问题；直接解法（direct-solution dynamic analysis procedure）：主要用于求解非线性动态问题。

提示：ABAQUS的所有单元均可用于动态分析，选取单元的一般原则与静力分析相同。

但在模拟冲击和爆炸载荷时，应选用一阶单元，因为它们具有集中质量公式，模拟应力波的效果优于二次单元所采用的一致质量公式。

[96] (pp281) 振型叠加法的基础是结构的各阶特征模态（eigenmode），因此在建模时要首先定义一个频率提取分析步（frequency extraction），从而得到结构的振型（mode shape）和固有频率（natural frequency），然后才能定义振型叠加法的各种分析步。

振型叠加法包括4种分析类型：（1）瞬时模态动态分析（transient modal dynamic analysis）计算线性问题在时域（time domain）上的动态响应。

用此分析要满足如下5个基本条件：(a) 系统是线性的（线性材料特性，无接触行为，不考虑几何非线性）。

(b) 响应只受相对较少的频率支配。

当在响应中频率的成分增加时（例如打击和碰撞问题），振型叠加法的效率将会降低。

(c) 载荷的主要频率应该在所提取的频率范围之内，以确保对载荷的描述足够精确。

(d) 特征模态应该能精确地描述任何突然加载所产生的初始加速度。

(e) 系统的阻尼不能过大。

（2）基于模态的稳态动态分析（mode-based steady-state dynamic analysis）在用户指定频率内的谐波激励下，计算引起结构响应的振幅和相位，得到的结果是在频域（frequency domain）上的。

ABAQUS的CEL分析什么是ABAQUSABAQUS是一种强大的有限元分析软件，常被用于求解结构力学和热力学问题。

它可以帮助工程师和科学家进行复杂结构的建模和分析，提供了多种功能模块，如静力学、动力学、热力学和电磁学等。

其中，CEL (Coupled Eulerian-Lagrangian)分析是ABAQUS中的一种特殊分析方法，用于模拟固体或液体中相对运动的结构。

CEL分析的原理CEL方法将物体划分为Eulerian网格和Lagrangian粒子，分别用于描述固体和流体的运动。

Eulerian网格是一种固定的网格，在整个分析过程中不发生变形，用于描述流体介质的运动。

Lagrangian粒子则随物体表面的移动而移动，用于描述固体物体的运动。

这种耦合的方法可用于模拟多种情况，如液体冲击、爆炸、钣金成形等。

CEL分析的步骤要进行CEL分析，需要执行以下步骤：1. 准备模型首先，需要准备一个包含所有几何和材料属性的模型。

这个模型可以是由CAD软件创建的几何模型，也可以是ABAQUS中的几何建模工具创建的模型。

在模型中，需要定义材料的本构关系、初始应力状态和初始速度等信息。

2. 离散网格在进行CEL分析之前，需要进行离散网格的划分。

将模型划分为适当的单元（element），以便进行数值计算。

在CEL分析中，需要同时划分Eulerian网格和Lagrangian粒子。

3. 定义物理耦合CEL分析的核心是定义Eulerian网格和Lagrangian粒子之间的物理耦合关系。

这通常包括流体与固体之间的接触、传热、质量传输等。

通过定义这些物理耦合关系，可以模拟出复杂的物理现象。

4. 定义加载条件加载条件是指施加在模型上的外部力和约束条件。

在CEL分析中，外部力可以是流体的冲击、爆炸力等，约束条件可以是固体的几何限制或边界条件。

5. 求解模型在进行CEL分析之前，需要设置求解器的参数和时间步长。

然后，通过ABAQUS的求解器对模型进行求解。