华中农业大学数学考研真题试题2007—2012、2016、2017年
- 格式:pdf
- 大小:8.48 MB
- 文档页数:30
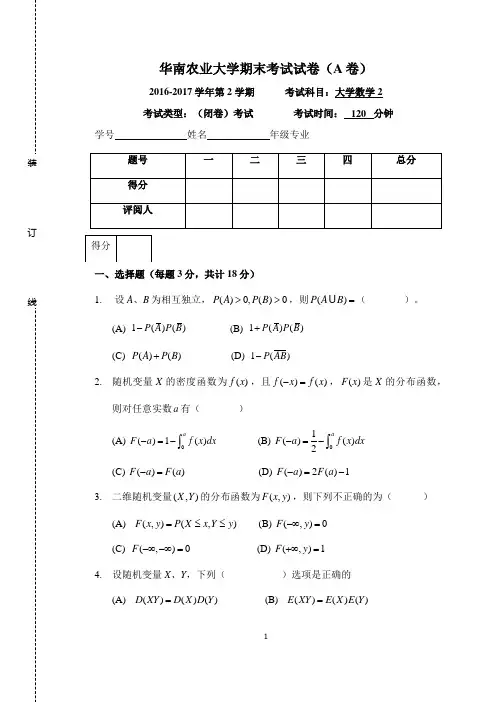
1 华南农业大学期末考试试卷(A 卷)2016-2017学年第 2 学期 考试科目:大学数学2 考试类型:(闭卷)考试 考试时间: 120 分钟学号 姓名 年级专业________________________一、选择题(每题3分,共计18分)1. 设A 、B 为相互独立,()0,()0P A P B >>,则()P A B =( )。
(A) 1()()P A P B - (B) 1()()P A P B + (C) ()()P A P B + (D) 1()P AB -2. 随机变量X 的密度函数为()f x ,且()()f x f x -=,()F x 是X 的分布函数,则对任意实数a 有( )(A) 0()1()aF a f x dx -=-⎰ (B) 01()()2a F a f x dx -=-⎰ (C) ()()F a F a -= (D) ()2()1F a F a -=-3. 二维随机变量(,)X Y 的分布函数为(,)F x y ,则下列不正确的为( )(A) (,)(,)F x y P X x Y y =≤≤ (B) (,)0F y -∞= (C) (,)0F -∞-∞= (D) (,)1F y +∞= 4. 设随机变量X 、Y ,下列( )选项是正确的(A) ()()()D XY D X D Y = (B) ()()()E XY E X E Y =2 (C) ()()()E X Y E X E Y +=+ (D) ()()()D X Y D X D Y -=- 5. 若样本12,n X X X 来自于正态分布总体2(,)N μσ,其中标准差σ已知,则对于均值μ的置信度为1α-的区间估计为( )(A) 22[((X t n X t n αα--+-(B) 22[X X ααμμ-+(C) 22[X u X u αα-+(D) [X u X u αα-+6. 若样本12,n X X X 来自于正态分布总体2(,)N μσ,其中期望μ已知,在假设检验20:16H σ=与21:16H σ≠中,使用的检验统计量为( )(A)22116nii Xμ=-∑ (B)21()16nii Xμ=-∑(C)21()16nii XX =-∑ (D)22116nii XX =-∑二、填空题(每空3分,共计18分)1. 已知()P A =0.5,()P B =0.6,(|)P B A =0.8,则()P A B =______________2. 设随机变量X 服从泊松分布(2)P ,则(2)P X ≤=_____________3. 连续型随机变量的分布函数220()00x a bex F x x -⎧⎪+≥=⎨⎪<⎩,则a =___ _______b=____________4. 假设~(1,4)X N -(正态分布),~(2)Y E (指数分布),且,X Y 相互独立,则(2)D X Y -= _________ 5. 样本12,n X X X 来自于正态分布总体2(,)N μσ,则样本均值X 服从___________________ (具体参数及分布)3三、计算题(每题8分,共计48分)1. 中国有两支球队上海上港队和广州恒大队参与亚冠联赛,根据数据分析知,上海上港队夺冠的概率为0.92,广州恒大队夺冠的概率为0.93。

华农往年试卷题 一、填空题 1. 幂级数2112(3)n n nn nx ∞-=+-∑的收敛半径R = 。
2. 幂级数21121n n x n +∞=+∑的收敛域为___________,和函数为________________.3.≤______及___________判别法可知1n ∞=__________上一致收敛.4. ()()12x xf x e e -=-在0x =处的泰勒展开式为___________________________,该展开式的收敛域为________________________. 5. 设函数21 ,0()1 ,0x f x x x ππ--<≤⎧=⎨+<≤⎩,则其以2π为周期的傅立叶级数在点x π=处收敛于 。
6. 1220lim 1a dxx ααα+→=++⎰_______________.二、判断题1. 设n n n a c b ≤≤,且数项级数n a ∑与n b ∑都收敛,则n c ∑一定收敛. ( )2. 在级数n u ∑的项中任意加括号,不改变级数的敛散性. ( )3. 设函数列(){}n f x 在[],a b 上一致收敛,且对任意n N ∈,()n f x 都是[],a b 上的可微函数,则()n f x '在[],a b 上也一致收敛. ( )4. 若数项级数n a ∑与n b ∑都收敛,则()2n n a b +∑一定收敛 。
( ) 5. 若11n nu u +≥,1,2,n =,则级数n u ∑发散。
( )6. 设n u ∑为正项级数 ,且11n nu u +<,则n u ∑收敛。
( ) 7. 设幂级数1n n n a x ∞=∑在区间I 上收敛于函数()f x ,且对一切n N ∈都有0n a ≠,则()f x 既不是奇函数也不是偶函数。
( )二、计算题1. 设40sin cos (0,1,2,)nn I x xdx n π==⎰,求级数0n n I ∞=∑的和。


华中农业大学二○○七年硕士研究生入学考试课程名称:食品化学一、名词解释(共20分,每题2分)1.疏水相互作用2.水分活度3.Maillard Reaction4.淀粉老化5.酸价6.油脂的自动氧化7.盐析作用8.Essential Amino Acids (并举一例) 9.肌红蛋白的氧合作用10.气味的阈值二、填空(共20分,每空1分)1.冷冻法保藏食品是利用了效应,而结冰对食品保藏有两种非常不利的后果,即和。
2.糖类化合物参与的褐变反应属于褐变,包括有和。
3.在高温下长时间加热的油炸油,酸价,黏度,发烟点,碘值。
4.稳定蛋白质三级结构的键力有、、、二硫键和等。
5.亚硝酸盐用于腌肉制品中的作用有、和。
6.面粉精制后白度,和减少。
三、单项选择题(每小题2分,共20分)1.体相水主要性质为。
A.不易结冰B.不能作为溶剂C.能被微生物利用D.热焓比纯水大2.油脂在Aw为的条件下贮存,稳定性最高。
A.0.22B.0.33C.0.55D.0.773.淀粉易老化的温度是。
A.60℃B.0℃C.-18℃D.2-4℃4.下列甜味剂中,可作糖尿病人甜味剂、不致龋齿的是。
A.蔗糖B.果糖C.麦芽糖D.木糖醇5.脂肪水解能引起。
A.酸价增高B.过氧化值降低C.碘值增高D. 酸价降低6.不饱和脂肪酸双键的几何构型通常用顺式、反式来表示。
天然不饱和脂肪酸多为构型。
A.无一定规律B.全顺式C.全反式D.绝大多数为反式7.下列不是必需氨基酸的是。
A.丝氨酸B.赖氨酸C.色氨酸D.亮氨酸8.蛋白质的水化作用对食品生产很重要,以下措施中不具有促进蛋白质水合性质的作用。
A.添加1%的氯化钠B.将温度从10℃调节至30℃C.添加30%的硫酸铵D.将pH 调节至远离等电点9.绿叶蔬菜在条件下最有利于保绿。
A.加碱B.加热C.加酸D.加酸、加热10.红烧肉中香气形成的途径是。
A.生物合成B.酶直接作用C.加热分解D.酶间接作用四、判断题:下列说法完全正确则打√,不完全正确则打×,并说明正确或不完全正确或错误的理由。


华中农业大学硕士研究生入学考试数学分析(628 )大纲试卷满分及考试时间试卷满分为150分,考试时间为180分钟.答题方式答题方式为闭卷、笔试.试卷题型结构单选题与填空题约50分解答题(包括证明题)约100分第一部分:实数集与函数,极限,连续考试内容:1.实数集的性质,实数集的上(下)确界。
2.实数完备性的基本定理。
3.函数的定义,函数的各种表示方法,基本初等函数的定义、性质及图像,复合函数、反函数、有界函数、周期函数、奇函数和偶函数、单调函数、初等函数的定义。
4.数列和函数极限的定义,数列和函数极限的性质。
5.数列的单调有界定理,数列和函数收敛的柯西收敛准则,归结原则。
6.两个重要极限及其应用。
7.无穷小量与无穷大量的概念及其阶的比较。
8.函数连续的概念,函数的间断点及其分类,复合函数与反函数的连续性。
9.闭区间上连续函数的性质。
10.函数的一致连续性的概念及相关结论。
考试要求:1.掌握实数集的有序性与稠密性,掌握实数集的上(下)确界的定义,会确定一些常见集合的上(下)确界。
2. 掌握实数完备性六个基本定理:确界原理、单调有界定理、区间套定理、有限覆盖定理、聚点定理和柯西收敛准则。
3. 掌握函数的定义,函数的各种表示方法;掌握基本初等函数的定义、性质及图像,掌握复合函数、反函数、有界函数、周期函数、奇函数和偶函数、单调函数、初等函数的定义。
4. 掌握数列极限的N -ε定义和函数极限的δε-定义,掌握数列和函数极限的唯一性、有界性、保号性、迫敛性、不等式性质以及四则运算性质,并会利用这些性质证明相关结论,求某些数列和函数的极限。
5. 掌握数列的单调有界定理,掌握数列和函数收敛的柯西收敛准则,掌握归结原则,并利用这些定理证明相关结论。
6. 掌握两个重要极限1sin lim 0=→x x x 与e x xx =+∞→)11(lim ,并应用这两个重要极限求其它相关数列或函数的极限。
7. 掌握无穷小量的概念,掌握无穷小量阶的比较,会应用无穷小量阶的比较证明相关结论,求相关极限;掌握大量的概念,掌握无穷大量与无穷小量之间的关系;会确定曲线的渐近线。

.2010 年全国硕士研究生入学统一考试农学门类联考数 学一、选择题: 1~8 小题,每小题 4 分,共 32 分,下列每题给出的四个选项中,只有一个选项符合题目要求,请将所选项前的字母填在答题纸... 指定位置上 .e x e 3 ( )(1) 设函数 f x,则x 3x e(A) x 3 及 x e 都是 f x 的第一类间断点(B) x 3 及 x e 都是 f x 的第二类间断点 (C) x 3 是 f x 的第一类间断点, x e 都是 f x 的第二类间断点(D)x 3 是 f x 的第二类间断点,x e 都是 f x 的第一类间断点x (2) 曲线 yx42 的凸弧区间是( )(A), 8(B)8, 4(C)4,4(D)4,(3) 设函数 f x , g x 具有二阶导数,g x 0a, g x 00, g x0 ,则 fg x 在x 0 取极大值的一个充分条件是( )(A)f a 0(B)f a(C)f a 0(D)f a 0设 函 数 fx0,1 上连续,0f x1 , 且1 x dx1(4) 在 区 间 f, 记21 11 1I 10 f x 1 f ydxdy , I 20 f x1 f ydxdy ,0 01 1I 30 f x f y dxdy ,则()(A) I 1 I 2 I 3(B) I 1 I 3 I 2(C) I 2 I 1 I 3 (D) I 3 I 2 I 1(5)设向量组I :1,,L 可由向量组II : 1 ,,L 线性表示,下列命题正确的是.() (A) 若向量组I 线性无关,则r s(B) 若向量组I线性相关,则r s (C) 若向量组II 线性无关,则r s(D) 若向量组II线性相关,则r s(6) 设A为 4 阶实对称矩阵,且A2 A 0,若A的秩为3,则A相似于( )1111(A)(B)11001111(C)(D)1100X1,1 上的均匀分布,事件 A0 X11,则( )4(A)P AB0(B)P AB P A(C)P A P B1(D)P AB P A P B(8)设 X1 ,K , X n使来自总体N, 20 的简单随机样本,记统计量T 1 n X i2,则n i 1 ET()(A)2(B)2(C)22(D)22二、填空题:9-14 小题,每小题 4 分,共 24 分,请将答案写在答题纸指定位置上 ....x x.(9) limx x a(10)曲线 y2x2sin x的水平渐近线的方程为y.cos x x2(11)已知一个长方形的长x 以0.2m/s的速率增加,宽y以0.3m/s的速率增加,当x12m ,y 5m时,其面积增加的速率为..函数 zy x1的全微分 dz(12)y 在点 1,e1,e.(13) 设 A1 1 1 , A T 为 A 的转置矩阵,则行列式 A T A.1 23(14) 设随机变量 X 的概率分布为 P X kk 1, k 1,2,L ,其中 01,若1P X25,则PX 3.9三、解答题: 15- 23 小题,共 94 分 .请将解答写在答题纸 指定的位置上 .解答应写出文字说...明、证明过程或演算步骤 .(15)( 本题满分 10 分)设函数 f ( )ln tanxexcos2x ,求 f ( )22(16)( 本题满分 10 分)2计算定积分x cos xdx(17)( 本题满分 11 分 )设某农作物长高到0.1 m 后,高度的增长速率与现有高度y 及 1 y 之积成比例 (比例系数 k 0),求此农作物生长高度的变化规律 (高度以 m 为单位 ).(18)( 本题满分 11 分 )计算二重积分sin( ) ,其中区域( ) 22.Ixxy dxdy Dx, y xy 2, x 1D(19)( 本题满分10 分)1x1证明: 1e( x 0) .x(20)( 本题满分 10 分)a 1 1 2设 A 0 a 10 , 1 11a1已知线性方程组 Ax有 2 个不同的解,求 a 的值和方程组 Ax的通解 ..(21)( 本题满分 11 分 )111设 A24a, 6 是A的一个特征值,335(I) 求a的值; (II) 求A的全部特征值和特征向量 .(22)( 本题满分 10分)设二维随机变量(X , Y) 的概率分布为Y101X010a 311b1 4121且 p X Y 1|X0求.3(I)常数 a, b ;(II) C ov( X ,Y) .(23)(本题满分11 分 )X x , 1 x 1,2,求设随机变量的概率密度为令f x Y X 10,其他。

经过一年的努力奋斗终于如愿以偿考到自己期望的学校,在这一年的时间内,我秉持着天将降大任于斯人也必先苦其心志劳其筋骨饿其体肤空乏其身的信念终于熬过了这段难熬却充满期待和自我怀疑的岁月。
可谓是痛并快乐着。
在这期间,我不止一次地怀疑自己有没有可能成功上岸,这样的想法,充斥在我的头脑中太多次,明知不可想这么多,但在休息时,思想放空的时候就会凭空冒出来,难以抵挡。
这对自己的心绪实在是太大的干扰,所以在此想跟大家讲,调整好心态,无论成功与否,付出自己全部的努力,到最后,总不会有那种没有努力过而与成功失之交臂的遗憾。
总之就是,付出过,就不会后悔。
在此,我终于可以将我这一年来的所有欣喜,汗水,期待,惶惑,不安全部写出来,一来是对这一重要的人生转折做一个回顾和告别,再有就是,希望我的这些经验,可以给大家以借鉴的作用。
无论是心态方面,考研选择方面,还是备考复习方面。
都希望可以跟大家做一个深入交流,否则这一年来的各种辛酸苦辣真是难吐难吞。
由于心情略微激动了些,所以开篇部分可能略显鸡汤,不过,认真负责的告诉大家,下面的内容将是满满的干货。
只是由于篇幅过长还望大家可以充满耐心的把它看完。
文章结尾会附赠我的学习资料供各位下载使用。
华中农业大学数学的初试科目为:(101)思想政治理论(201)英语一(628)数学分析和(870)高等代数参考书目为:1.《数学分析(第四版)》,华东师范大学数学系编,高等教育出版社.2.《高等代数(第四版)》,北京大学数学系几何与代数教研室前代数小组编,高等教育出版社.3.高等代数,北京大学数学系前代数小组编(第四版),北京:高等教育出版社,2013首先简单介绍一下我的英语复习经验。
⑴单词:英语的单词基础一定要打好,如果单词过不了关,那你其他可以看懂吗??单词可以用木糖英语单词闪电版就够了。
也可以用app软件。
但是这样就会导致玩手机(如果你自制力超强),单词的话到考前也不能停止的。
我的单词并没有背好,导致英语后来只有60+,很难过…⑵阅读:阅读分数很高,所以一定要注重,可以听木糖英语的名师讲解,或者木糖英语的课程,阅读最重要的是自己有了自己的方法,有一个属于自己的做题方法可以节省很多时间,如果初次做题还没有什么思路,那就可以多看看真题里面的答案解析考研英语很难,和四六级是完全不同的!大家肯定都听说过,所以阅读暑假就可以开始做了,真题反复摸索,自己安排好时间。

农学数学考研真题答案在准备农学数学考研的过程中,真题练习是不可或缺的一部分。
真题能够让你了解考试的难度和题型,同时也有助于检验你的学习效果。
以下是一些关于农学数学考研真题答案的示例内容,请注意,这些内容是虚构的,仅用于示例,实际的答案需要根据具体的真题来确定。
农学数学考研真题答案示例一、选择题1. 题目:若函数\( f(x) \)在区间\( [a, b] \)上连续,则下列哪个选项是正确的?- A. \( f(x) \)在\( [a, b] \)上单调递增- B. \( f(x) \)在\( [a, b] \)上存在最大值和最小值- C. \( f(x) \)在\( [a, b] \)上可能没有最大值- D. \( f(x) \)在\( [a, b] \)上可能没有最小值答案:B2. 题目:若\( \lim_{x \to a} f(x) = L \),则下列哪个选项是错误的?- A. \( f(x) \)在\( x = a \)处可能无定义- B. \( f(x) \)在\( x = a \)处可能取到\( L \)- C. \( f(x) \)在\( x = a \)处不可能取到\( L \)- D. \( f(x) \)在\( x = a \)处的左极限和右极限都存在答案:C二、填空题1. 若\( \int_{0}^{1} x^2 dx \)的值为\( \frac{1}{3} \),则\( \int_{0}^{1} x dx \)的值为______。
答案:\( \frac{1}{2} \)2. 若\( y = \ln(x) \),则\( \frac{dy}{dx} \)的值为______。
答案:\( \frac{1}{x} \)三、解答题1. 题目:证明\( \lim_{x \to 0} \frac{\sin(x)}{x} = 1 \)。
证明:首先,我们知道\( \sin(x) \)的泰勒展开式为\( \sin(x)= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots \)。