Matlab仿真实例-卫星轨迹

用M A T L A B计算G P S 卫星位置-最新文档资料用MATLAB计算GPS卫星位置GPS定位的基本原理简单来说就是在WGS-84空间直角坐标系中，确定未知点与GPS卫星的空间几何关系。

因此利用GPS 进行导航和测量时，卫星是作为位置已知的高空观测目标。

那么如何精确快速的解算出卫星在空间运行的轨迹即其轨道是实现未知点快速定位的关键。

1 标准格式RINEX格式简述在进行GPS数据处理时，由于接收机出自于不同厂家，所以厂家设计的数据格式也是五花八门的，但是在实际中，很多时候需要把来自不同型号的接收机的数据放在一块进行处理，这就需要数据格式的统一，为了解决这种矛盾，RINEX（英文全称为：The Receiver Independent Exchange Format）格式则应运而生，该格式存储数据的类型是文本文件，数据记录格式是独立于接收机的出自厂家和具体型号的。

由此可见，其特点是：由于是通用格式，所以可将不同型号接收机收集的数据进行统一处理，并且大多数大型数据处理软件都能够识别处理，此外也适用于多种型号的接收机联合作业，通用性很强。

RINEX标准文件里不是单一的一个文件，而是包括如下几种类型的文件[1]。

（1）观测数据文件（ssssdddf.yyo），记录的是GPS观测值信息，（OBServation data，简写OBS，为接收机记录的伪距、相位观测值；O文件，如XG012191.10O）。

（2）导航电文文件（ssssdddf.yyn），记录的是GPS卫星星历信息（NAVavigation data，简写NAV，记录实时发布的广播星历；N文件，如XG012191.10N）。

（3）气象数据文件（ssssdddf.yym），主要是在测站处所测定的气象数据（METerological data，简写MET，记录气象仪器观测的温、压、湿度状况；M文件，如XG012191.10M）。

（4）GLONASS导航电文文件（ssssdddf.yyg），记录的是地球同步卫星的导航电文。

GPS卫星轨道计算及其MATLAB仿真黎奇，白征东，李帅，陈波波（清华大学地球空间信息研究所，北京 100084）一、程序设计思路1. 读取RINEX文件（注意：文件路径）2. 计算测量日周积秒（测量日的格里历→GPST）3. 按卫星轨道计算步骤计算WGS-84坐标系坐标（内插）4. 按需要将WGS-84坐标系下坐标转换为所需坐标系坐标5. 画图输出二、n 文件说明及读取程序参考时刻oe t 的RINEX 格式的 “”广播星历文件具体如下：（加粗部分为本次轨道化Ω，率i ，弧度/秒4-22）标svacc ，米）收到的卫星信号解，秒）文件名：RinexNreader.m 输 入：文件地址，卫星编号三、计算测量日的周积秒文件名：GCtoGPS.m （其中调用函数：GCtoJD.m）输入：指定公历的年、月、日、时、分、秒文件名：GCtoJD.m输 入：指定公历的 年、月、日四、GPS 卫星轨道计算步骤及计算程序1. 计算卫星运动的平均角速度n平均角速度()03n =经摄动参数n ∆改正后的平均角速度0n n n =+∆3#61-79），n ∆（2#42-60）；14323.98600510/GM m s =⨯ 2. 计算归化时间k t说明：①广播星历是oe t 时刻的，对应的轨道参数也是oe t 时刻的，而观测时间在t 时刻，显然oe t t ＜。

所以，要想获得t 时刻的轨道参数，需要知道t 与oe t 之间的差值即k t 。

以此，按照oe t 时刻轨道参数，外推t 时刻轨道参数。

②k t 的起算时间是星期六/星期日子夜0点，当302400k t s ＞时，604800k t s -；当302400k t s ＜-时，+604800k t s 。

（604800s=1周） =k oe t t t -，且604800302400604800302400k k k k k k t t t t t t =-⎧⎨=+⎩＞ ＜-已知：oe t （1#4-21）3. 计算观测时刻的平近点角k M0k k M M nt =+已知：0M （2#61-79），n （见1），k t （见2） 4. 计算观测时刻的偏近点角k Esin k k k E M e E =+已知：k M （见3），e （3#23-41）方法：迭代解算，设初值0k k E M =，迭代2次基本收敛。

嫦娥一号与月亮、地球、太阳关系演示图欧阳仕粮学号：20084051014（吉首大学物理与机电工程学院，湖南吉首416000）摘要：用matlab模拟嫦娥一号人造卫星运围绕月球做周期性运动时，人造卫星、月球、地球相对于太阳的运动轨迹动画。

展现了人造卫星绕月飞行时相对与参照物太阳的运动轨迹，便于直观的了解卫星相对于太阳的相对运动。

关键词：卫星运动轨迹;相对运动;数学软件matlab1、引言大家都知道我们所了解的地球围绕太阳做近似圆周运动的规则运动，当然月球，人造地球卫星也是如此，而我们一直以来所关注的登月工程的探月卫星也是这样一种情况。

那月球、探月卫星嫦娥一号相对于太阳是一个怎样的情形，下面通过计算机软件matlab，来模拟一下月球、嫦娥一号相对太阳的运动动画，并描绘出轨迹。

2、原理假设我们所研究的所有星体处在同一水平面上。

地球距太阳的的平均距离为R，月球距地球的平均距离为r1，嫦娥一号距月球的平均距离为r2，地球公转角速度w1，月亮公转角速度w2，嫦娥一号绕月亮公转角速度w3。

我们从0每隔0.01到2 取一个弧度s1。

地球相对太阳转过的角度sita1，月亮相对地球转过的角度sita2，嫦娥一号相对月球转过的角度sita3，设开始时间为t=0,然后每隔时间T进行一次取样计算，计算各个星体的的位置坐标。

首先，确定太阳的位置为（0，0），根据圆周运动的轨迹方程确定地球的运行轨道（R*cos(s1),R*sin(s1)），确定月球围绕地球公转的轨道(R*cos(sita1)+r1*cos(s1),R*sin(sita1)+r1*sin(s1))，再确定画嫦娥一号绕月亮公转轨道(R*cos(sita1)+r1*cos(sita1)+r2*cos(s1),R*sin(sita1)+r1*sin(sita1)+r2*sin(s1))，这样就找出了地球、月球、嫦娥一号的轨迹。

分别在matlab中用plot函数画出。

低轨卫星轨道仿真matlab低轨卫星轨道仿真可以使用MATLAB进行,以下是一个简单的步骤:1. 建立模型:首先需要建立一个低轨卫星模型。

这个模型可以基于卫星的物理参数,如质量、轨高度、自转等参数。

这些参数可以通过现有的卫星数据集或者自己计算获得。

2. 建立方程:在建立模型的同时,需要建立一个方程来描述卫星的运动。

这个方程可以使用牛顿第二定律或万有引力定律等经典物理学方程进行建模。

3. 运行仿真:使用MATLAB中的Simulink模块运行仿真。

Simulink提供了丰富的工具箱,可以帮助建模和仿真复杂的系统。

在Simulink中,可以使用运动仿真工具箱来仿真卫星的运动。

4. 可视化结果:在仿真运行结束后,可以使用MATLAB中的plot 模块来可视化结果。

将卫星的运动轨迹、速度、轨道高度等数据可视化出来,以便更好地理解卫星的运动行为。

下面是一个简单的低轨卫星轨道仿真的MATLAB代码示例,假设我们使用仿真工具箱来模拟卫星的运动:```matlab% 建立模型model = reshape(load("低轨卫星模型.mat"), [1 1 3]);model.M = [10.0 8.0 6.0]; % 卫星质量model.H = [300.0 200.0 200.0]; % 轨道高度model.Z = [0.1; 0.15; 0.2]; % 卫星轨道中心距地面的高度 model.V = [0.9; 0.94; 0.97]; % 卫星的速度% 建立方程F = 1.0; % 引力常数,近似为1g = 9.8; % 重力加速度,近似为9.8米/秒^2M = model.M; % 卫星质量h = model.H - 2*model.Z; % 卫星轨道中心距地面的高度model.P = 1.0; % 卫星的公转周期% 运行仿真Time = 0:0.01:1; % 仿真时间,单位为秒X = model.V*Time; % 卫星的X坐标Y = model.V*Time + h/2; % 卫星的Y坐标Z = model.V*Time + 3*h/2; % 卫星的Z坐标plot(X, Y, Z, "b"); % 可视化卫星的运动轨迹title("低轨卫星轨道仿真结果");```在这个代码中,我们使用了牛顿第二定律和万有引力定律来建立卫星的运动方程。

MATLAB卫星轨迹引言卫星轨迹是描述卫星在地球或其他天体之间运动的路径。

通过了解卫星轨迹，我们可以预测和控制卫星的运行，以及计划卫星的任务。

在本文档中，我们将使用MATLAB来分析和绘制卫星轨迹。

确定卫星轨迹方程卫星在空间中的运动可以通过多种方式描述，其中一种常用的方法是使用开普勒问题的解析解。

开普勒问题是描述两个质点间引力相互作用的运动方程。

对于一个质点沿着椭圆轨道运动的情况，其运动方程可以表示为：轨道方程轨道方程其中，r是卫星与中心天体（例如地球）之间的距离，a和b是椭圆的半长轴和半短轴，e是离心率，θ是卫星相对于半长轴的偏移角。

在MATLAB中，我们可以使用以下代码来计算卫星的轨道方程：function [x, y] = compute_orbit(a, e, theta)r = a * (1 - e^2) ./ (1 - e * cos(theta));x = r .* cos(theta);y = r .* sin(theta);end绘制卫星轨迹在计算了卫星的轨道方程之后，我们可以使用MATLAB的绘图工具将卫星轨迹可视化。

以下是绘制卫星轨迹的代码示例：a = 6378; % 半长轴e = 0.1; % 离心率theta = linspace(0, 2*pi, 1000); % 角度范围[x, y] = compute_orbit(a, e, theta);figure;plot(x, y);axis equal;title('卫星轨迹');xlabel('X轴');ylabel('Y轴');在上述代码中，我们假设半长轴为6378千米，离心率为0.1，并生成1000个角度点。

然后，我们使用compute_orbit 函数计算卫星的轨道坐标，并使用plot函数绘制这些坐标。

最后，我们使用axis equal命令来确保图形的横纵比例相等，以保持轨道的形状准确。

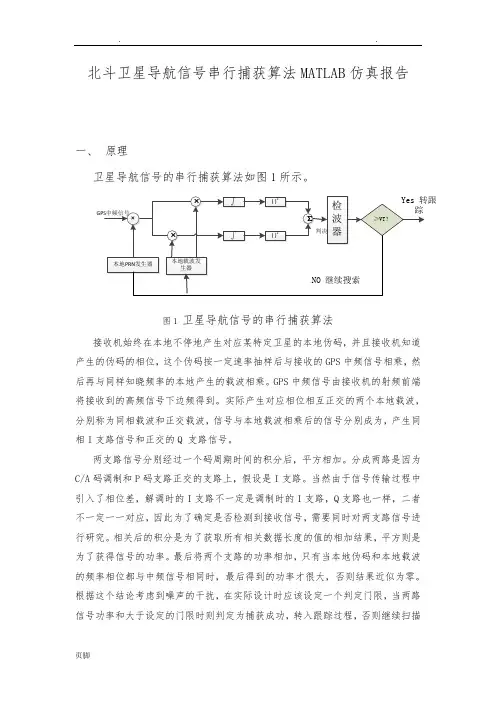
北斗卫星导航信号串行捕获算法MATLAB仿真报告一、原理卫星导航信号的串行捕获算法如图1所示。

图1 卫星导航信号的串行捕获算法接收机始终在本地不停地产生对应某特定卫星的本地伪码，并且接收机知道产生的伪码的相位，这个伪码按一定速率抽样后与接收的GPS中频信号相乘，然后再与同样知晓频率的本地产生的载波相乘。

GPS中频信号由接收机的射频前端将接收到的高频信号下边频得到。

实际产生对应相位相互正交的两个本地载波，分别称为同相载波和正交载波，信号与本地载波相乘后的信号分别成为，产生同相I支路信号和正交的Q 支路信号。

两支路信号分别经过一个码周期时间的积分后，平方相加。

分成两路是因为C/A码调制和P码支路正交的支路上，假设是I支路。

当然由于信号传输过程中引入了相位差，解调时的I支路不一定是调制时的I支路，Q支路也一样，二者不一定一一对应，因此为了确定是否检测到接收信号，需要同时对两支路信号进行研究。

相关后的积分是为了获取所有相关数据长度的值的相加结果，平方则是为了获得信号的功率。

最后将两个支路的功率相加，只有当本地伪码和本地载波的频率相位都与中频信号相同时，最后得到的功率才很大，否则结果近似为零。

根据这个结论考虑到噪声的干扰，在实际设计时应该设定一个判定门限，当两路信号功率和大于设定的门限时则判定为捕获成功，转入跟踪过程，否则继续扫描其它的频率或相位。

二、MATLAB仿真过程及结果仿真条件设置：抽样频率16MHz，中频5MHz，采样时间1ms，频率搜索步进1khz，相位搜索步进1chip，信号功率-200dBW，载噪比55dB（1）中频信号产生卫星导航信号采用数字nco的方式产生，如图2所示。

载波nco控制字为：carrier_nco_word=round(f_carrier*2^N/fs); 伪码nco控制字为：code_nco_word=round(f_code*2^N/fs);图 2其中载波rom存储的是正弦信号的2^12个采样点，伪码rom存储长度为2046的卫星伪码。

使用Matlab绘制卫星星下点轨迹1.地球静止轨道卫星，倾角分别为0，30，90度。

clc; clear;t = 0:1:6;we = 360/24;u = we*t;i = 30;fai = asind( sind(i)*sind(u) );deltalmd = atand( cosd(i)*tand(u) );if(i==90)deltalmd(end) = 90;endlmd = deltalmd - we*t;% use symetry to generate the other datafor j = 1:6lmd(j+7) = -lmd(7-j);fai(j+7) = fai(7-j);endfor j = 1:12lmd(j+13) = lmd(13-j);fai(j+13) = -fai(13-j);endh = geoshow('landareas.shp', 'FaceColor', [1 1 1]); grid onhold onplot(lmd, fai); title(['GEO¹ìµÀ£¬Çã½Çi=', num2str(i)])-200-150-100-50050100150200GEO轨道，倾角i=30-200-150-100-50050100150200-200-150-100-50050100150200-200-150-100-50050100150200GEO 轨道，倾角i=90-200-150-100-500501001502002.回归轨道卫星，回归周期1天，倾角分别为60度，周期为4h。

clc; clear;t = [0 1/3 1/2 2/3 4/5 1];we = 360/24;w = 180/2;u = w*t;i = 60;fai = asind( sind(i)*sind(u) );deltalmd = atand( cosd(i)*tand(u) );lmd = deltalmd - we*t;% use symetry to generate the other datafor j = 1:5lmd(j+6) = lmd(6) + ( lmd(6) - lmd(6-j) );fai(j+6) = fai(6-j);endfor j = 1:10if (lmd(11) + ( lmd(11) - lmd(11-j) )) > 180lmd(j+11) = -180 + rem(lmd(11) + ( lmd(11) - lmd(11-j) ), 180);elselmd(j+11) = lmd(11) + ( lmd(11) - lmd(11-j) );endfai(j+11) = -fai(11-j);endcnt = 1;for m = 1:5for j = 1:21if (lmd(j+21*(m-1)) + 60) > 180lmd(j+21*m) = -180 + rem(lmd(j+21*(m-1)) + 60, 180);record(m,cnt) = j; % record when tranverse from east to westcnt = cnt + 1;elselmd(j+21*m) = lmd(j+21*(m-1)) + 60;endfai(j+21*m) = fai(j+21*(m-1));endcnt = 1;endload stillh = geoshow('landareas.shp', 'FaceColor', [1 1 1]);grid onhold onplot(lmd1(2:20), fai1(2:20), 'b--'); % earth stillplot(lmd(1:6), fai(1:6), 'bo');plot(lmd(21*6), fai(21*6), 'bo');plot(lmd(1:13), fai(1:13)); plot(lmd(14:21), fai(14:21));for m = 1:5plot(lmd(21*m+1:record(m,1)+21*m-1), fai(21*m+1:record(m,1)+21*m-1)); plot(lmd(record(m,1)+21*m:21*(m+1)), fai(record(m,1)+21*m:21*(m+1)));plot(lmd(21*m), fai(21*m), 'bo');endtitle(['ÐÇϵã¹ì¼££ºT=4h¹ìµÀ£¬Çã½Çi=', num2str(i)])T=4h轨道，倾角i=60-200-150-100-50050100150200星下点轨迹：T=4h轨道，倾角i=60-200-150-100-50050100150200地球不转时的星下点clc; clear;t = [0 1/3 1/2 2/3 4/5 1];we = 360/24;w = 180/2;u = w*t;i = 60;fai = asind( sind(i)*sind(u) );deltalmd = atand( cosd(i)*tand(u) );lmd = deltalmd; % earth still% use symetry to generate the other datafor j = 1:5lmd(j+6) = lmd(6) + ( lmd(6) - lmd(6-j) );fai(j+6) = fai(6-j);endfor j = 1:10if (lmd(11) + ( lmd(11) - lmd(11-j) )) > 180lmd(j+11) = -180 + rem(lmd(11) + ( lmd(11) - lmd(11-j) ), 180);elselmd(j+11) = lmd(11) + ( lmd(11) - lmd(11-j) );endfai(j+11) = -fai(11-j);endfor j = 1:21if (lmd(j) + 180) > 180lmd(j) = -180 + rem(lmd(j) + 180, 180);elselmd(j) = lmd(j) + 180;endfai(j) = fai(j);endlmd(11) = 0;lmd1 = lmd;fai1 = fai;save still lmd1fai1h = geoshow('landareas.shp', 'FaceColor', [1 1 1]);grid onhold onplot(lmd(2:20), fai(2:20));% plot(lmd(1:13), fai(1:13)); plot(lmd(14:21), fai(14:21));% for m = 1:5% plot(lmd(21*m+1:record(m,1)+21*m-1), fai(21*m+1:record(m,1)+21*m-1)); plot(lmd(record(m,1)+21*m:21*(m+1)), fai(record(m,1)+21*m:21*(m+1)));% endtitle(['T=4h¹ìµÀ£¬Çã½Çi=', num2str(i)])T=4h轨道，倾角i=60-200-150-100-50050100150200。

配套毕业设计论文见百度文库请搜索《基于MATLAB的GPS信号仿真123》附录C 仿真程序代码1、数据码的产生function datacode=data(x)y=rand(1,x);for i=1:xif y(i)<0.5datacode(i)=0;elsedatacode(i)=1;endendy(1)=0;show2(1)=datacode(1);q=2;for i=1:length(datacode)for j=1:100y(q)=i-1+j*0.01;show2(q)=datacode(i);q=q+1;endendplot(y,show2);axis([0 length(datacode) -0.2 1.2]);1、C/A码的产生及扩频调制clc;c=input('请输入数据码的长度：c=');y=rand(1,c);for i=1:cif y(i)<0.5datacode(i)=0;elsedatacode(i)=1;endendx(1)=0;show(1)=datacode(1);p=2;for i=1:cfor j=1:100x(p)=i-1+j*0.01;show(p)=datacode(i);p=p+1;endendsubplot(4,1,1);plot(x,show);title('数据码');axis([0 c -0.2 1.2]);number=input('请输入卫星PRN号码:number=');cacode=CAgenerate(number);temp=cacode(1:100)x(1)=0;show(1)=temp(1);p=2;%下面的循环是为了将结果显示成方波形式 for i=1:length(temp)for j=1:100x(p)=i-1+j*0.01;show(p)=temp(i);p=p+1;endend%画出仿真结果图subplot(4,1,2);plot(x,show);title('C/A码');axis([0 100 -0.2 1.2]);%截取CA码的前十个数据进行扩频，每个数据插入5个CA序列cacode1=cacode(1:10);for i=1:cif datacode(i)==1datacodek((i-1)*50+1:i*50)=ones(1,50);elsedatacodek((i-1)*50+1:i*50)=zeros(1,50);endendfor i=1:cfor j=1:50addr=rem(((i-1)*50+j),10);if addr==0addr=10;endkuopindata((i-1)*50+j)=xor(datacodek((i-1)*50+j),cacode1(addr));endend%下面的循环是为了将结果显示成方波形式x(1)=0;show(1)=kuopindata(1);p=2;for i=1:length(kuopindata)for j=1:100x(p)=i-1+j*0.01;show(p)=kuopindata(i);p=p+1;endendsubplot(4,1,3);plot(x,show);title('扩频数据');axis([0 length(kuopindata) -0.2 1.2]);%每位数据通过正弦波来调制Sinwave=sin([0:2*pi/8:2*pi*7/8]);Sinwave=single(Sinwave);GPSsignal=zeros(1,1);Sinwave=[Sinwave Sinwave Sinwave Sinwave Sinwave];for i=1:length(kuopindata)GPSsignal=[GPSsignal kuopindata(i)*Sinwave];endGPSsignal=GPSsignal(2:length(GPSsignal));subplot(4,1,4);plot(GPSsignal(1:500));title('调制后数据');C/A码产生的子程序CAgenerate：function cacode=CAgenerate(number)if (number<1)|(number>37)disp('输入参数必须在1 ～ 37之间取值');returnendCACode=zeros(1,1023); %生成一个1*1023的零矩阵% 设置寄存器初相Reg1=[1,1,1,1,1,1,1,1,1,1];Reg2=[1,1,1,1,1,1,1,1,1,1];% 设置反馈点,1表示需要反馈gp1=[0,0,1,0,0,0,0,0,0,1];gp2=[0,1,1,0,0,1,0,1,1,1];% 抽头G2Table=[ 2,3,4,5,1,2,1,2,3,2,3,5,6,7,8,9,1,2,3,4,5,6,1,4,5,6,7,8,1,2,3,4,5,4,1,2,4;6,7,8,9,9,10,3,4,6,7,8,9,10,4,5,6,7,8,9,3,6,7,8,9,10,6,7,8,9,10,10,7,8,10;]% 生成一个周期的伪码序列for m=1:1023CACode(m)=mod(Reg1(10)+Reg2(G2Table(1,number))+Reg2(G2Table(2,number)),2); Reg1=[mod(Reg1*gp1',2),Reg1(1:9)];Reg2=[mod(Reg2*gp2',2),Reg2(1:9)];endcacode=CACode;2、C/A码的相关性分析clc;n=input('请输入卫星PRN号码:n=');cacode1=CAgenerate(n);%在G2序列中找出-1并转换为0,找出1并转换为1ind1=find(cacode1==1);ind2=find(cacode1==0);cacode1(ind1)=-ones(1,length(ind1));cacode1(ind2)=ones(1,length(ind2));N=1023;z=zeros(1,1023);for i=0:N-1for k=i+1:N-1z1(k)=cacode1(k)*cacode1(k-i); z(i+1)=z(i+1)+z1(k);endz(i+1)=z(i+1)/N;endsubplot(2,1,1);plot(z);title('自相关特性');axis([-50 1300 -0.5 1.2]);n=input('请输入卫星PRN号码:n='); cacode2=CAgenerate(n);ind1=find(cacode2==1);ind2=find(cacode2==0);cacode2(ind1)=-ones(1,length(ind1)); cacode2(ind2)=ones(1,length(ind2)); N=1023;h=zeros(1,1023);for i=0:N-1for k=i+1:N-1h1(k)=cacode1(k)*cacode2(k-i); h(i+1)=h(i+1)+h1(k);endh(i+1)=h(i+1)/N;endsubplot(2,1,2);plot(h);title('互相关特性');axis([-50 1300 -0.5 1]);4、 P码的产生及扩频调制clc;c=input('请输入数据码的长度：c=');y=rand(1,c);for i=1:cif y(i)<0.5datacode(i)=0;elsedatacode(i)=1;endendx(1)=0;show(1)=datacode(1);p=2;for i=1:cfor j=1:100x(p)=i-1+j*0.01;show(p)=datacode(i);p=p+1;endendsubplot(4,1,1);plot(x,show);title('数据码');axis([0 c -0.2 1.2]);NumberPCode=input('enter the NumberPcode='); NumberShift=input('enter the NumberShift=');a=input('enter a=');pcode=Pcode(a,NumberPCode,NumberShift);x(1)=0;show(1)=pcode(1);p=2;for i=1:length(pcode)for j=1:100x(p)=i-1+j*0.01;show(p)=pcode(i);p=p+1;endendsubplot(4,1,2);plot(x,show);title('P码');axis([0 length(pcode) -0.2 1.2]);pcode=pcode(1:10);for i=1:cif datacode(i)==1datacodek((i-1)*50+1:i*50)=ones(1,50);elsedatacodek((i-1)*50+1:i*50)=zeros(1,50);endendfor i=1:cfor j=1:50addr=rem(((i-1)*50+j),10);if addr==0addr=10;endkuopindata((i-1)*50+j)=xor(datacodek((i-1)*50+j),pcode(addr));endendx(1)=0;show(1)=kuopindata(1);p=2;%下面的循环是为了将结果显示成方波形式for i=1:length(kuopindata)for j=1:100x(p)=i-1+j*0.01;show(p)=kuopindata(i);p=p+1;endendsubplot(4,1,3);plot(x,show);title('扩频数据');axis([0 length(kuopindata) -0.2 1.2]);%每位数据通过正弦波来调制Sinwave=sin([0:2*pi/8:2*pi*7/8]);Sinwave=single(Sinwave);GPSsignal=zeros(1,1);Sinwave=[Sinwave Sinwave Sinwave Sinwave Sinwave]; for i=1:length(kuopindata)GPSsignal=[GPSsignal kuopindata(i)*Sinwave];endGPSsignal=GPSsignal(2:length(GPSsignal));subplot(4,1,4);title('调制后数据');plot(GPSsignal(1:500));以下是P码产生的子程序Pcode:function pcode=Pcode(a,NumberPCode,NumberShift) % P码产生reg1a=[0 0 0 1 0 0 1 0 0 1 0 0];reg1b=[0 0 1 0 1 0 1 0 1 0 1 0];reg2a=[1 0 1 0 0 1 0 0 1 0 0 1];reg2b=[0 0 1 0 1 0 1 0 1 0 1 0];rx1a=0;rx1b=0;rx2a=0;rx2b=0;x1bWork=1;x2aWork=1;x2bWork=1;N=NumberShift;C1=4092*3750;C2=4093*3749;z1a=mod(N,4092);%取余数x1a=mod([(N-z1a)/4092],3750);y1a=(N-z1a-4092*x1a)/C1;if ((N-C1*y1a)>=C2)z1b=4092;x1bWork=0;x1b=3748;elsez1b=mod((N-C1*y1a),4093);x1bWork=1;x1b=(N-z1b-C1*y1a)/4093;endm=mod(N,(C1+37));y2a=(N-m)/(C1+37);if (m>=C1)dv=m-C1;elsedv=0;endz2a=mod((m-dv),4092);x2a=mod((((m-dv)-z2a)/4092),3750);z2b=mod((m-dv),4093);if (m>=C2)x2b=3748;elsex2b=(m-z2b)/4093;end%各移位寄存器的状态for i=1:z1aslave1a=mod(reg1a(6)+reg1a(8)+reg1a(11)+reg1a(12),2);reg1a(2:12)= reg1a(1:11);reg1a(1)=slave1a;endfor i=1:z1bslave1b=mod(reg1b(1)+reg1b(2)+reg1b(5)+reg1b(8)+reg1b(9)+reg1b(10)+reg1b(11)+ reg1b(12),2);reg1b(2:12)=reg1b(1:11);reg1b(1)=slave1b;endfor i=1:z2aslave2a=mod(reg2a(1)+reg2a(3)+reg2a(4)+reg2a(5)+reg2a(7)+reg2a(8)+reg2a(9)+reg2a(10) +reg2a(11+reg2a(12)) ,2);reg2a(2:12)=reg2a(1:11);reg2a(1)=slave2a;endfor i=1:z2bslave2b=mod(reg2b(2)+reg2b(3)+reg2b(4)+reg2b(8)+reg2b(9)+reg2b(12) ,2); reg2b(2:12)=reg2b(1:11);reg2b(1)=slave2b;end%各控制变量的判断if z1a==4091rx1a=1;endif z1b==4092rx1b==1;endif z2a==4091rx2a=1;x2aWork=0;endif z2b==4092rx2b=1;x2bWork=0;end%开始产生P码p=zeros(NumberPCode,1);x1acou=0;x1bcou=0;x2acou=0;x2bcou=0;cou37=dv;x2(1:a)=1;for i=1:(NumberPCode+37)x1(i)=mod( reg1a(12)+reg1b(12),2);x2(i+a)=mod( reg2a(12)+reg2b(12),2);%寄存器x1b的移位函数if x1bWork==1if rx1b==0slave1b=mod(reg1b(1)+reg1b(2)+reg1b(5)+reg1b(8)+reg1b(9)+reg1b(10)+reg1b(11)+reg1b(12),2);reg1b(2:12)=reg1b(1:11);reg1b(1)=slave1b;else if rx1b==1reg1b=[0 0 1 0 1 0 1 0 1 0 1 0];rx1b=0;endendelse if x1bWork==0endendif reg1b==[0 1 0 1 0 1 0 1 0 1 0 0 ]rx1b=1;x1bcou=x1bcou+1;if x1bcou==3749x1bwork=0;x1bcou=0;endend%寄存器x1a的移位函数if rx1a==0slave1a=mod(reg1a(6)+reg1a(8)+reg1a(11)+reg1a(12),2);reg1a(2:12)=reg1a(1:11);reg1a(1)=slave1a;else if rx1a==1reg1a=[0 0 0 1 0 0 1 0 0 1 0 0];rx1a=0;endendif reg1a==[0 0 1 0 0 1 0 0 1 0 0 0]rx1a=1;x1acou=x1acou+1;if x1acou==3750x1bwork=1;x1acou=0;endend%寄存器x2b的移位函数if x2bWork==1if rx2b==0slave2b=mod(reg2b(2)+reg2b(3)+reg2b(4)+reg2b(8)+reg2b(9)+reg2b(12) ,2); reg2b(2:12)=reg2b(1:11);reg2b(1)=slave2b;else if rx2b==1x2bout=reg2b(11);reg2b=[0 0 1 0 1 0 1 0 1 0 1 0];rx2b=0;endendelse if x2bWork==0reg2b=[0 0 1 0 1 0 1 0 1 0 1 0];x2bWork=1;rx2b=0;endendif reg2b==[0 1 0 1 0 1 0 1 0 1 0 0]rx2b=1;x2bcou=x2bcou+1;if x2bcou==3749x2bWork=0;x2bcou=0;endend%寄存器x2a的移位函数if x2aWork==1if rx2a==0slave2a=mod(reg2a(1)+reg2a(3)+reg2a(4)+reg2a(5)+reg2a(7)+reg2a(8)+reg2a(9)+reg2a(10)+reg2a(11)+reg2a(12) ,2); reg2a(2:12)=reg2a(1:11);reg2a(1)=slave2a;else if rx2a==1reg2a=[1 0 1 0 0 1 0 0 1 0 0 1];rx2a=0;endendelse if x2aWork==0if rx2a==1cou37=cou37+1;if cou37==37rx2a=0;x2awork=1;cou37=0;endendendendif reg2a==[0 1 0 0 1 0 0 1 0 0 1 1]rx2a=1;x2acou=x2acou+1;if x2acou==3750x2awork=0;x2acou=0;endendendfor i=1:NumberPCodep(i)= mod( x1(i)+x2(i),2);endp=p';pcode=p';5、 P码的相关性分析clc;NumberPCode=input('enter the number Pcode='); NumberShift=input('enter the numbershift=');a=input('enter a=');pcode=Pcode(a,NumberPCode,NumberShift); ind1=find(pcode==1);ind2=find(pcode==0);pcode(ind1)=-ones(1,length(ind1));pcode(ind2)=ones(1,length(ind2));M=NumberPCode;z=zeros(1,M);for i=0:M-1for k=i+1:M-1z1(k)=pcode(k)*pcode(k-i);z(i+1)=z(i+1)+z1(k);endz(i+1)=z(i+1)/M;endsubplot(2,1,1);plot(z);title('自相关特性');axis([-50 M -0.5 1.2]);a=input('enter a=');NumberShift=input('enter the numbershift='); pcode2=Pcode(a,NumberPCode,NumberShift); h=zeros(1,M);for i=0:M-1for k=i+1:M-1h1(k)=pcode(k)*pcode2(k-i);h(i+1)=h(i+1)+h1(k);endh(i+1)=h(i+1)/M;endsubplot(2,1,2);plot(h);title('互相关特性');axis([-50 M -0.5 1]);。

MATLAB模拟多星系统中行星运动摘要自古人类就在仰望星空，思考宇宙的奥秘。

人类在宇宙中是否是孤单的，有没有外星生命，这是一个许多人都想知道的问题，人们对现实宇宙进行了许多的研究，想要诞生生命，有一颗可以为行星提供稳定且适合能量的恒星是必不可少的。

在旧版《星球大战》电影中，有一幕标志性的场景，卢克·天行者在塔图因沙漠欣赏令人震撼的双落日奇观。

那么这种双星甚至多星系统，行星的运动是怎样的呢？本文就此问题利用MATLAB进行了仿真模拟。

关键词：多星系统，MATLAB仿真，行星运动1 研究背景与意义太阳，对于我们地球上的万物来说，非常重要，将太阳称为“万物之源”也不为过。

我们地球之所以能够具备孕育生命的条件，一个很重要的因素就是地球处于太阳系的宜居地带，如果不是在太阳系的宜居地带，而是离太阳很近或者比较遥远，意味着地球表面的温度会比较高或者比较低，要么像水星、金星那样高温，要么像土星、木星那样寒冷。

天空中出现一个太阳，对于我们来说刚刚好的，如果多一个太阳，地球可能就会变得很高温，地球是否还能孕育生命都是一个大问题。

那么多星系统中，是否也可以存在宜居带呢？行星在多星系统中的运动又是如何呢？双星系统中的行星是一个三体问题，用现有的数学工具无法给出一般情况下的解析解。

本文模拟了一颗行星围绕一颗双星的轨道，该双星由一颗具有太阳质量的恒星和另一颗具有太阳质量一半的恒星组成。

恒星系统的周期是30个地球日。

本文的研究范围进一步缩小到恒星系统平面内的行星运动，有效地使其成为一个二维问题。

行星可能环绕整个恒星系统运行，可能是两颗恒星中的一颗，也可能是拉格朗日点。

本文采用数值积分方法模拟了行星的运动。

定义恒星系的时变引力场，然后制定描述行星运动的微分方程。

在模拟结束时，检查这颗行星是否仍然在围绕恒星系统的轨道上。

2 天体运动理论2.1 双星系统的运动方程首先，我们看一下恒星系统中恒星的运动方程。

这是一个两体问题，可以通过在原点放置一颗恒星而转化为一个等效的一体问题。

用MATLAB计算GPS卫星位置摘要:本文主要介绍了GPS测量数据的常用格式RINEX标准文件格式,并利用MA TLAB工具计算出所观测卫星里的五颗卫星(14、20、29、31和32五颗)在283个历元的瞬时位置,即所观测时间段里五颗卫星在WGS-84坐标下的空间运行轨迹。

关键词:RINEX标准文件WGS-84下卫星位置MATLAB工具GPS定位的基本原理简单来说就是在WGS-84空间直角坐标系中,确定未知点与GPS卫星的空间几何关系。

因此利用GPS进行导航和测量时,卫星是作为位置已知的高空观测目标。

那么如何精确快速的解算出卫星在空间运行的轨迹即其轨道是实现未知点快速定位的关键。

1 标准格式RINEX格式简述在进行GPS数据处理时,由于接收机出自于不同厂家,所以厂家设计的数据格式也是五花八门的,但是在实际中,很多时候需要把来自不同型号的接收机的数据放在一块进行处理,这就需要数据格式的统一,为了解决这种矛盾,RINEX(英文全称为:The Receiver Independent Exchange Format)格式则应运而生,该格式存储数据的类型是文本文件,数据记录格式是独立于接收机的出自厂家和具体型号的。

由此可见,其特点是:由于是通用格式,所以可将不同型号接收机收集的数据进行统一处理,并且大多数大型数据处理软件都能够识别处理,此外也适用于多种型号的接收机联合作业,通用性很强。

RINEX标准文件里不是单一的一个文件,而是包括如下几种类型的文件[1]。

2 卫星坐标的计算步骤由于在GPS定位和导航的时候,用户都是把GPS卫星的位置作为已知量来对待,并且GPS定位所用的坐标系是世界大地坐标系WGS-84。

所以就先必须根据GPS接收机观测的相应星历数据,解算出GPS卫星在WGS-84坐标系中的瞬时位置。

为了后面计算方便,先对广播星历中涉及到的计算卫星坐标的一些轨道参数进行说明,如表4所示。

由于每隔两个小时,GPS接收机收到的广播星历才更新一次,所以用户在根据接收机收到的卫星导航电文汇总的广播星历参数推算GPS的瞬时坐标的时候,一定要选取与GPS卫星的瞬时坐标时刻最相近的那组广播星历数据[2],否则误差将会很大。

地球卫星三维运行轨道MATLAB 仿真1、问题的描述轨道上运行的地球卫星，根据牛顿第二定律T F ；以及万有引力定律F--OmM s *7/?可得 JGM ii •加 即h PM JHr 3,户-GMJWr'； r=∙^x a +y 2+z 2大力MJW ⑴式中，(x, y, z)表示卫星的三维坐标，为G=6∙672∙ΠΓ”(N ∙m2∕kg2)引力常数, M L 5S7∙1024(⅛)是地球的质量。

假定卫星的三个方向的初始位置和速度如下该卫星轨道求解过程实际上是求解一个二阶常微分方程，可首先将该方程转 换为一阶常微分方程，令X=RyaK,y ⅛τ,故公式(1)可转化为Γ X (4)]X(S)X (6)∣Λ∙X(1)∣ I A ∙X(2)∣L^∙X(3)J初始条件即为MH>M3BQ2J7 UUΛia U41Ml.n MnM _407Jfl MIUfl]2、MATLAB 仿真代码分两段程序：(1)子程序将二阶微分方程转换为一阶微分方程，代码如下 function fy=vdp(t, x)r=x(l) ^2+x (2) ^2+x(3) ^2;G=3. 986005el4;A=-G∕r^(3/2);fy=[χ(4)x (5)x (6)A*x(l)XQ) = Λ=-GM B ∕Γ3AA*x (2)A*x(3)];End(2)主程序如下，注意：为更好地查看卫星轨道与地球的相对位置关系，此处将地球模型图的绘制代码一并给出clear allclose allclcyθ=[2043922. 1667658186504. 631471 4343461.7147915379. 544693 -407. 095342 3516. 052656];[t, result] =ode45(@vdp, [0:1:9000], yθ);x=result(:, 1);y=result(:, 2);z=result(:, 3);[X, Y, Z] =sphere (200);RE=O. 64e7;X=RE*X;Y=RE*Y;Z=RE*Z;figured)hold ongrid onmesh (X, Y, Z)%绘制地球plot3(x, y, z)%绘制卫星轨道仿真结果如下(给出两张图)：。

基于MATLABSimulink的GPS卫星导航仿真器设计摘要：本文首先介绍了GPS卫星定位的原理和算法，然后给出了GPS仿真器的Simulink建模实现方法，并对其定位精度进行了误差分析，仿真结果表明该仿真器定位精度与实际接收机相当，可以用来模拟真实的卫星定位，为综合导航系统的研制工作带来了便利。

关键词：GPS卫星导航Simulink建模动态仿真1 引言现代飞行器对导航系统有着越来越高的要求，尤其是长航时飞机对导航设备的精度、可靠性以及连续性都提出了全面的要求。

每种导航系统都有其固有的局限性，因此仅靠单一系统的导航设备独立使用难以完全满足这些要求。

于是，使用多种导航技术的综合导航系统逐渐进入人们的视线，并受到广泛关注。

由于飞行实验费用大，对于综合导航系统最初的算法验证和实验测试，往往无法进行飞行器搭载实验，因此国内外均采用实验室半物理仿真系统进行初期实验研究。

Simulink是一种针对动态系统进行建模、仿真和分析的工具，它被广泛应用于线性系统、非线性系统的建模和仿真，支持连续系统、离散系统或者两种混合的系统和多速率系统。

本文介绍了“大飞机”综合导航仿真系统中，基于MATLAB/Simulink开发的GPS仿真器的原理和设计过程。

2 仿真器的应用环境如图1所示，综合导航仿真系统由飞行、惯导、卫星导航、天文导航、大气数据仿真、无线电高度表、地形匹配导航等分系统仿真器加上显控系统构成。

本文述及的工作主要集中于综合导航仿真系统中卫星导航仿真器的设计及其Simulink建模实现。

飞行仿真器有手动操作和自动飞行两种控制模式，自动飞行模式下仿真器根据预设航线输出飞机实时位置、速度、加速度、姿态等参数；手动模式下通过外置手柄来模拟操作飞机完成起飞、爬升、平飞、姿态改变和降落等全过程，飞行仿真器根据手柄传感器的输出信息仿真计算输出飞机的飞行数据。

卫星导航仿真器接收来自飞行仿真器的输出作为飞机当前实际位置，进行定位解算。

卫星轨迹一．问题提出设卫星在空中运行的运动方程为：其中是k 重力系数(k=401408km3/s ）。

卫星轨道采用极坐标表示，通过仿真，研究发射速度对卫星轨道的影响。

实验将作出卫星在地球表面（r=6400KM ，θ=0)分别以v=8KM/s,v=10KM/s, v=12KM/s 发射时,卫星绕地球运行的轨迹。

二．问题分析1．卫星运动方程一个二阶微分方程组，应用Matlab 的常微分方程求解命令ode45求解时，首先需要将二阶微分方程组转换成一阶微分方程组。

若设 ,则有：2．建立极坐标如上图所示，初值分别为：卫星径向初始位置，即地球半径:y(1，1)=6400；卫星初始角度位置：y(2，1)=0；卫星初始径向线速度：y(3,1)=0;卫星初始周向角速度：y(4，1）=v/6400。

3．将上述一阶微分方程及其初值带入常微分方程求解命令ode45求解，可得到一定时间间隔的卫星的径向坐标值y （1）向量；周向角度坐标值y(2)向量;径向线速度y(3）向量；周向角速度y(4)向量。

4．通过以上步骤所求得的是极坐标下的解,若需要在直角坐标系下绘制卫星的运动轨迹,还需要进行坐标变换,将径向坐标值y （1)向量;周向角度坐标值y （2)向量通过以下方程转换为直角坐标下的横纵坐标值X,Y 。

5．卫星发射速度速度的不同 将导致卫星的运动轨迹不同，实验将绘制卫星分别以v=8KM/s ，v=10KM/s ，v=12KM/s 的初速度发射的运动轨迹。

三．Matlab 程序及注释1．主程序v=input （'请输入卫星发射速度单位Km/s ：\nv='）； %卫星发射速度输入.axis （[—26400 7000 -10000 42400 ]); ％定制图形输出坐标范围.%为了直观表达卫星轨迹，以下语句将绘制三维地球.[x1，y1，z1］=sphere(15）； ％绘制单位球。

x1=x1＊6400;y1=y1＊6400； ⎪⎪⎩⎪⎪⎨⎧-=+-=dt d dt dr r dt d dt d r r k dt r d θθθ2)(222222θ==)2(,)1(y r y ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧**-=**+*-===)1(/)4()3(2)4()4()4()1()1()1()3()4()2()3()1(y y y dt dy y y y y y k dt dy y dt dy y dt dy ⎩⎨⎧*=*=)]2(sin[)1(Y )]2(cos[)1(X y y y yz1=z1＊6400；％定义地球半径。

MATLAB在航空航天领域中的应用与实践案例导言航空航天领域一直以来都是科技创新的前沿领域之一，众多重大的科学发现和技术突破都与航空航天领域紧密相关。

而MATLAB这一强大的数值计算软件在航空航天领域中的应用也备受关注。

本文将介绍MATLAB在航空航天领域中的应用与实践案例，探讨其在航空航天领域中的重要意义。

第一章：航空航天领域中的数据分析与处理在航空航天领域中，海量的数据需要进行分析和处理，以提取有价值的信息。

MATLAB作为一款强大的数据分析工具，在此领域中发挥着重要作用。

1.1 数据预处理在航空航天领域中，数据质量对研究和决策都有重要影响。

而MATLAB提供了丰富的预处理函数和工具，可以对原始数据进行去噪、滤波、插值等操作，提高数据的准确性和可靠性。

1.2 数据可视化数据可视化对于理解和分析数据具有重要意义。

MATLAB提供了丰富的绘图函数和工具箱，可以将复杂的数据进行可视化展示，帮助研究人员更好地理解数据特征和规律。

案例1：基于MATLAB的飞机故障诊断系统航空领域中，飞机故障诊断是一项非常重要的任务。

研究人员使用MATLAB 开发了一套飞机故障诊断系统，通过对传感器数据进行实时监测和分析，可以自动检测和诊断出飞机故障，并及时采取相应措施。

这一系统的成功应用，大大提高了飞机的安全性和可靠性。

第二章：飞行控制与导航系统2.1 飞行控制算法MATLAB可用于开发飞行控制算法，如自动驾驶、姿态控制等。

其强大的数值计算能力和丰富的工具箱使得开发高效、稳定的飞行控制系统变得更加容易。

2.2 导航系统设计导航系统在航空领域中起着至关重要的作用。

MATLAB提供了多种导航系统设计工具和算法，可用于开发惯性导航系统、卫星导航系统等，帮助飞行器在复杂环境中准确导航。

案例2：基于MATLAB的无人机避障算法设计无人机避障是航空领域中的一项重要研究。

研究人员使用MATLAB开发了一套无人机避障算法，通过对周围环境的感知和分析，可以自动避开障碍物，确保无人机的安全飞行。

卫星绕地球旋转演示动画clc,clear,close allh=figure('numbertitle','off','name','卫星绕地球旋转演示动画');%设置标题名字s1=0:.01:2*pi;hold on;axis equal; %建立坐标系axis off; %除掉Axesr1=10; %地球到太阳的平均距离r2=3; %卫星的轨道半径w1=1; %设置地球公转角速度w2=12; %设置卫星绕地球公转角速度t=0; %初始时刻pausetime=.002; %设置视觉暂留时间sita1=0;sita2=0;%设置开始它们都在水平线上set(gcf,'doublebuffer','on') %消除抖动plot(-20,18,'color','r','marker','.','markersize',40);text(-17,18,'太阳');%对太阳进行标识plot(-20,16,'color','b','marker','.','markersize',20);text(-17,16,'地球');%对地球进行标识plot(-20,14,'color','w','marker','.','markersize',13);text(-17,14,'卫星');%对卫星进行标识plot(0,0,'color','r','marker','.','markersize',60);%画太阳plot(r1*cos(s1),r1*sin(s1));%画地球公转轨道set(gca,'xlim',[-20 20],'ylim',[-20 20]);p1=plot(r1*cos(sita1),r1*sin(sita1),'color','b','marker','.','markersize',30);%地球初始位置l1=plot(r1*cos(sita1)+r2*cos(s1),r1*sin(sita1)+r2*sin(s1));%画卫星绕地球的公转轨道p2x=r1*cos(sita1)+r2*cos(sita2);p2y=r1*sin(sita1)+r2*sin(sita2);p2=plot(p2x,p2y,'w','marker','.','markersize',20);%画卫星的初始位置orbit=line('xdata',p2x,'ydata',p2y,'color','r');%画卫星的运动轨迹while 1if ~ishandle(h),return,endset(p1,'xdata',r1*cos(sita1),'ydata',r1*sin(sita1));%设置地球的运动过程set(l1,'xdata',r1*cos(sita1)+r2*cos(s1),'ydata',r1*sin(sita1)+r2*sin(s1));%设置卫星绕地球的公转轨道的运动过程ptempx=r1*cos(sita1)+r2*cos(sita2);ptempy=r1*sin(sita1)+r2*sin(sita2);set(p2,'xdata',ptempx,'ydata',ptempy);%设置卫星的运动过程p2x=[p2x ptempx];p2y=[p2y ptempy];set(orbit,'xdata',p2x,'ydata',p2y);%设置卫星运动轨迹的显示过程sita1=sita1+w1*pausetime;%地球相对太阳球转过的角度sita2=sita2+w2*pausetime;%卫星相对地球转过的角度pause(pausetime); %视觉暂停drawnow %刷新屏幕，重绘end。

基于MATLAB的GPS信号的仿真研究一、本文概述随着全球定位系统（GPS）技术的广泛应用，其在导航、定位、授时等领域的重要性日益凸显。

为了更好地理解GPS信号的特性，提高GPS接收机的设计水平和性能，对GPS信号进行仿真研究显得尤为重要。

本文旨在探讨基于MATLAB的GPS信号仿真方法，分析GPS信号的特点，以及如何利用MATLAB这一强大的数值计算环境和图形化编程工具，对GPS信号进行高效、精确的仿真。

文章首先介绍了GPS系统的发展历程、基本原理和信号特性，为后续的信号仿真提供了理论基础。

随后，详细阐述了GPS信号仿真的一般流程，包括信号生成、传播模型、噪声添加等关键环节。

在此基础上，重点介绍了如何利用MATLAB编写GPS信号仿真程序，包括信号生成、传播模型建立、噪声模拟等方面的具体实现方法。

文章还通过实际案例，展示了基于MATLAB的GPS信号仿真在接收机设计、性能评估等方面的应用。

通过仿真实验，可以深入了解GPS信号在不同环境下的传播特性，为接收机算法优化和性能提升提供有力支持。

本文的研究不仅有助于加深对GPS信号特性和仿真方法的理解，也为GPS接收机的研究和开发提供了一种有效的技术手段。

通过MATLAB的仿真研究，可以更加直观地揭示GPS信号的本质规律，为实际应用提供有力指导。

二、GPS信号原理及特性全球定位系统（GPS）是一种基于卫星的无线电导航系统，它利用一组在地球轨道上运行的卫星来提供全球范围内的定位和时间服务。

每个GPS卫星都不断地向地球表面发射射频信号，这些信号被地面上的接收器接收并处理，从而确定接收器的三维位置和速度，以及精确的时间信息。

GPS卫星发射的信号是L波段的射频信号，分为两个频段：L1（142 MHz）和L2（160 MHz）。

每个频段都包含两种类型的信号：C/A码（粗捕获码）和P码（精密码）。

C/A码是对公众开放的，用于民用和商业应用，而P码则用于军事和特定的高精度应用。

利用加速度和陀螺仪数据绘制轨迹主要涉及数据采集、数据处理和数据可视化三个步骤。

以下是一个简要的实现方法：
1. 数据采集：首先，需要一个能够获取加速度和陀螺仪数据的设备。

这些设备通常内置在智能手机或特定传感器中。

然后，通过MATLAB的设备驱动程序，例如Acquisition Engine，可以获取这些数据流。

你需要设定数据采集的频率、数据格式等参数。

2. 数据处理：在获取原始数据后，需要进行预处理和特征提取。

例如，你可能需要过滤掉噪声，补偿重力加速度，以及提取角速度和角位置信息。

这些都可以通过MATLAB的信号处理工具箱完成。

3. 数据可视化：最后，你需要将处理后的数据可视化。

MATLAB的图形和可视化工具箱可以用来绘制轨迹图。

例如，你可以使用plot函数绘制二维或三维轨迹图。

如果你想进行更复杂的可视化，例如绘制速度或加速度随时间变化的图表，可以使用plotyy或stairs函数。

这只是一个基础的实现方法。

实际的应用可能需要进行更复杂的处理和优化，例如对数据进行滤波、插值、特征提取和分类等。

你也可能需要将MATLAB与其他的工具或语言集成，例如用于机器学习的Python库。

总的来说，利用加速度和陀螺仪数据绘制轨迹是一个多步骤的过程，需要综合考虑数据获取、处理和可视化的各个方面。

MATLAB提供了一套完整的工具箱，可以帮助你快速开发和实现这些功能。