道路竖曲线计算表

二、竖曲线的计算方法1.圆曲线形竖曲线计算《铁路线路设计规范》规定：Ⅰ、Ⅱ级铁路竖曲线半径为10000m Tv=5 X △i ，Ⅲ级铁路竖曲线半径为5000m。

Tv=2.5 X △i(1)竖曲线的切线长Tv=Rv ×tan a/2 = Rv/2 ×tan a= Rv/2000 ×△i △i=△i2-△i1 的绝对值Tv－竖曲线的切线长(m)；Rv--竖曲线半径，a----竖曲线转角，△i－相邻坡段坡度的代数差(‰)。

(2)竖曲线的曲线长C≈2T。

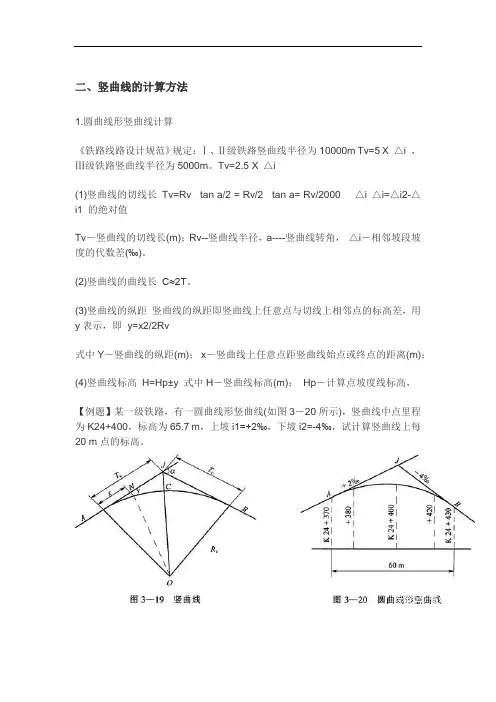
(3)竖曲线的纵距竖曲线的纵距即竖曲线上任意点与切线上相邻点的标高差，用y表示，即y=x2/2Rv式中Y－竖曲线的纵距(m)；x－竖曲线上任意点距竖曲线始点或终点的距离(m)；(4)竖曲线标高H=Hp±y 式中H－竖曲线标高(m)；Hp－计算点坡度线标高，【例题】某一级铁路，有一圆曲线形竖曲线(如图3－20所示)，竖曲线中点里程为K24+400，标高为65.7 m，上坡i1=+2‰，下坡i2=-4‰，试计算竖曲线上每20 m点的标高。

【解】①计算△i相邻坡段坡度的代数差(‰) △i1-△i2=2-(-4)=6‰②竖曲线的切线长Tv=5·△i=5×6=30 m③竖曲线的曲线长C≈2Tv=2×30=60m④竖曲线的坡度线标高、纵距、标高计算。

竖曲线的起点计算A=K24+400-30=K24+370竖曲线的终点计算B=K24+400+30=K24+430各点坡度线标高K24+370 Hp =65.7-30×2‰=65.64K24+380 Hp H=65.7-20×2‰=65.66K24+400 Hp =65.7K24+420 Hp =65.7-20×4‰=65.62K24+430 Hp =65.7-30×4‰=65.58纵距计算K24+380 和K24+420 纵距y=10×10/2×10000=0.005K24+400 纵距y=30×30/2×10000=0.045 Y=C×C/8R=60×60/8×10000=0.045 纵距K24+370 和K24+430纵距为0竖曲线标高H(m) H=Hp±y竖曲线标高计算表2.抛物线型竖曲线计算(1)竖曲线的长度c=△i/γ.20(m)式中△i－相邻坡段坡度的代数差(‰)；γ－每20m长度的变坡率(‰)，由表3－17查得。

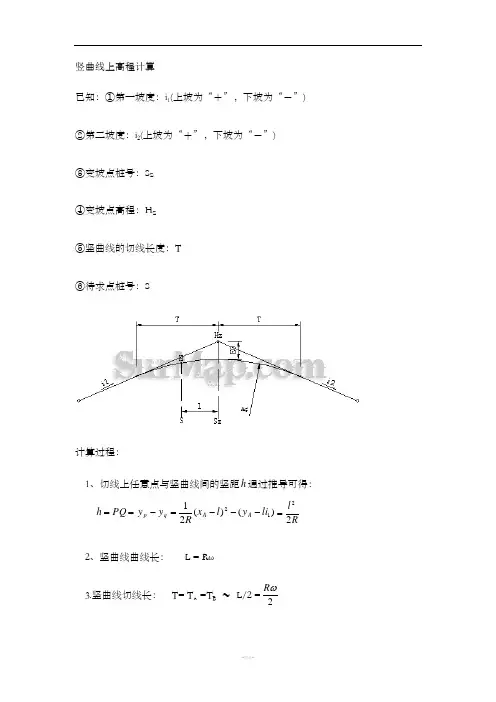
竖曲线上高程计算
已知：①第一坡度：i 1(上坡为“＋”，下坡为“－”)
②第二坡度：i 2(上坡为“＋”，下坡为“－”)
③变坡点桩号：S Z
④变坡点高程：H Z
⑤竖曲线的切线长度：T
⑥待求点桩号：S
计算过程：
1、切线上任意点与竖曲线间的竖距h 通过推导可得：
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长： L = R ω
3.竖曲线切线长： T= T A =T B ≈ L/2 =
2ωR
4、竖曲线的外距： E =R
T 22
5. 竖曲线上任意点至相应切线的距离：R
x y 22= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；
R —为竖曲线的半径，m 。

竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤如下：
（1）计算竖曲线的基本要素：竖曲线长：L ；切线长：T ；外距：E 。

（2）计算竖曲线起终点的桩号： 竖曲线起点的桩号 = 变坡点的桩号－T
（3）计算竖曲线上任意点切线标高及改正值：
切线标高 = 变坡点的标高±（x T -）⨯i ；改正值：y=R
x 22 （4）计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y 某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－ y。

竖曲线铁路线路的纵断面最理想的当然是平道，然而事实上是不可能的，为了适应地形的起伏，以减少工程量，纵断面必须用各种不同的坡面连接而成。

两相邻坡段的连续点谓之变坡点。

相邻坡段的坡度差是两相邻坡段的坡度代数差。

当相邻坡段的坡度差超过允许值时，为了保证行车平顺和安全，应在变坡点处用竖曲线连接起来。

允许不设竖曲线的坡度差允许值是根据车轮不脱轨、车钩不脱钩、列车不撞车和行车平稳等要求进行分析确定的。

一般情况下，竖曲线采用圆曲线，也可以采用抛物线，个别情况下，还可以采用连续短坡曲线。

竖曲线的计算一、圆曲线形竖曲线圆曲线形竖曲线的几何要素和各点设计标高，可按下列公式计算，如图。

R α　x T TyRCα/2　BAi1i21、竖曲线的切线长度TT=R·tan(α/2)=R/2·tanα=R/2·△i‰=R/2000·△i(m) (5-1)式中 R-竖曲线半径(m)；α-竖曲线转角(度)；△i-相邻坡段的坡度代数差(‰)。

R=5000m时， T=2.5△i(m)R=10000m时，T=5.0△i(m)R=15000m时，T=7.5△i(m)R=20000m时，T=10.0△i(m)R=25000m时，T=12.5△i(m)2、竖曲线长度CC≈2T=R/1000·△i(m) (5-2)3、竖曲线纵距yy=x2/2R (m) (5-3)式中 x-竖曲线上计算点至竖曲线起(终)点的横距(m)。

当x=T时，变坡点的纵距Y即为竖曲线的外矢距E。

Y=E=T2/2R=1/2R(C/2)2=C2/8R (5-3.1)4、竖曲线上各点的设计标高H设h为计算点的坡度标高，则H=h±y (5-4)式中的y值，凹形取“+”，凸形取“-”。

【算例一】一凹形竖曲线i1=-4‰，i2=+2‰，△i=6‰，变坡点的里程为K235+165，标高为54.60m，R=15000m，计算竖曲线上各20m点的设计标高。

竖曲线计算公式
一、公路施工中经常见到线路竖向曲线计算标高的问题，采用近似计算方法以外耻距（E）变化量代替标高增减量计算，设和用于半径（R）大于5000m时，误差为0.2mm。

1、凸曲线：H计算=H起坡点+i×△L起坡点至计算点的距离-（1/conα-1）×R
2、凹面线:H计算=H起坡点- i×△L起坡点至计算点的距离+（1/conα-1）×R
二、公路施工中经常见到线路竖向曲线计算标高的问题，采用近似计算方法以外变高差（h）变化量代替标高增减量计算，适合用于半径（R）小于5000m时，误差为0.2mm。

1、凸曲线：H计算=H起坡点+ i×△L起坡点至计算点的距离-(△L起坡点至计算点的距离)2/2R
2、凹面线:H计算=H起坡点- i×△L起坡点至计算点的距离+(△L起坡点至计算点的距离)2/2R
三、计算时考虑是正方计算方向来确定公式变换，如果凹面曲线从坡度终点返算时：坡度值为正值采用2公式时就应为+（- i×△L）。

竖曲线要素及变坡点处设计高程计算 坡度计算：②竖曲线类型：当i n i i n 为正值时，为凹型竖曲线;当i n 1 i n 为负值时，为凸型竖曲线。

③由厘米坐标纸上，经过反复试坡、调坡，根据土石方填挖大致平衡和道。

坡长等设计要求最后确定出变坡点：变坡点1桩号：K 0 255.67，高程-0.9404m变坡点计算 ①变坡点一： 桩号 K 0255.67 , i 1 -0.150% i 2 0.220%R=21621.62m变坡点高程：-0.9404m A.计算竖曲线要素：i 2 i 10.37 %此时根据规范可知：该曲线为凹形曲线竖曲线几何要素中曲线长 L R 21621 0.37% 80( m )竖曲线几何要素中切线长T L 280 40m 2竖曲线几何要素中外距ET 2 402m 2R 2 21621. 0 .U37 111B.计算竖曲线起终点桩号 竖曲线起点桩号： K。

215・67竖曲线起点高程： -0.9404 40 0.15% -0.8804m竖曲线终点桩号： K295.67竖曲线终点高程：-0.9404 40 0.22% -0.8524m①坡度=高差 坡长设计规范中最小计算设计高程 由已 H 0 (T X 儿 H=H i h H:任一点切线的高程 x:计算点到起点的距离 i 1：坡度H:任一点的设计高程 曲线段内各点的设计高程: K0+220xX=24.33my0.0137m2R切线高程： 设计高程： -0.8804-24.33 X 0.15%= -0.9169m -0.9169+0.0137= -0.9032m K0+2602x X=35.67my 0.0294m2R切线高程： 设计高程： -0.8524-35.67 X 0.22%= -0.9309m -0.9309+0.0294= -0.9015m K0+280X=15.67m2x y0.0057 m切线高程： 设计高程： -0.8524-15.67 X 0.22%= -0.8869m -0.8869+0.0057= -0.8812m 直线段内各点设计咼程见下表：设计高程表高程咼程(m) -0.9032 桩号桩号 +240.000 K0+000 (m)-0.56 +20.000 -0.59 +260.000 -0.9015 +40.000 -0.62 +280.000 -0.8812 +60.000 -0.65+300.000 -0.8361 +80.000-0.68+320.000-0.7921切线高程： 设计高程： -0.8804-4.33 X 0.15%= -0.8869m-0.8869+0.0004= -0.8865m2x2R0.0004 m X=220-215.67=4.33mK0+2402+100.000 -0.71 +340.000 -0.7481+120.000 -0.74 +360.000 -0.7041 +140.000 -0.77 +380.000 -0.6601 +160.000 -0.80 +400.000 -0.6161 +170.000 -0.83 +420.000 -0.5721 +180.000 -0.86 +440.000 -0.5281+200.000 -0.89+220.000 -0.8865。

道路的竖曲线图XY轴比例一般横向1:1000，纵向1:100，如果起伏较大，纵向1:200（就是y轴）。

没有一定的规定。

但是纵横1:10看起来比较好看。

1. 近似计算公式如图1所示，设道路纵坡的变坡点为I，其设计高程为HI,里程为DI，两侧的纵坡度分别为i1、i2，竖曲线设计半径为R，竖曲线各元素的近似计算公式如下：2. 精确计算公式如图2所示，在图中建立以水平距离为横坐标轴d,铅垂线为纵坐标轴H′的dOH′直角坐标系，A点的坐标为(dA，0)，Z点的坐标为(0，HZ′)，竖曲线各元素的精确计算公式如下：α1＝arctani1(1)α2＝arctani2(2)ω＝α1-α2(3)T＝Rtan(4)E＝R(sec-1)(5)dI＝Tcosα1(6)dA＝Rsinα1(7)HZ′＝Rcosα1(8)竖曲线在直角坐标系中的方程为：(d-dA)2+H′2＝R2(9)由式(9)可推算出竖曲线上任一与Z点的里程差为d的点的纵坐标值H′，则0≤d≤dY(10)并可立即推算点的设计高程和里程：H＝H′-ΔH(11)D＝DZ+d(DZ＝DI-dI)(12)式中，α1，α2分别为纵坡线与水平线的夹角；ω为变坡角；Τ为切线长；Ε为外矢距；dI为纵坡变坡点I与Z点的里程差；dA 为竖圆曲线圆心A与Z点的里程差；H′为竖圆曲线上任一点的纵坐标值；d为竖圆曲线上任一点与Z点的里程差；H为竖圆曲线上任一点的设计高程；ΔH＝H′Z-HZ为Z点纵坐标值与Z点设计高程之差(HZ＝HI-dI.i1)；D为竖曲线上任一点的里程。

由式(10)可知，当d=dA时，则里程DN＝DZ+dA的N点为竖圆曲线的变坡点，其高程HN＝HN′-ΔH＝R-ΔH＝max，N点在现场施工中具有很重要的指导意义。