下载文档原格式
第一章 差分方程差分方程是连续时间情形下微分方程的特例。
差分方程及其求解是时间序列方法的基础，也是分析时间序列动态属性的基本方法。
经济时间序列或者金融时间序列方法主要处理具有随机项的差分方程的求解问题，因此，确定性差分方程理论是我们首先需要了解的重要内容。
§1.1 一阶差分方程假设利用变量t y 表示随着时间变量t 变化的某种事件的属性或者结构，则t y 便是在时间t 可以观测到的数据。
假设t y 受到前期取值1-t y 和其他外生变量t w 的影响，并满足下述方程：t t t w y y ++=-110φφ (1.1)在上述方程当中，由于t y 仅线性地依赖前一个时间间隔自身的取值1-t y ，因此称具有这种结构的方程为一阶线性差分方程。
如果变量t w 是确定性变量，则此方程是确定性差分方程；如果变量t w 是随机变量，则此方程是随机差分方程。
在下面的分析中，我们假设t w 是确定性变量。
例1.1 货币需求函数 假设实际货币余额、实际收入、银行储蓄利率和商业票据利率的对数变量分别表示为t m 、t I 、bt r 和ct r ，则可以估计出美国货币需求函数为：ct bt t t t r r I m m 019.0045.019.072.027.01--++=-上述方程便是关于t m 的一阶线性差分方程。
可以通过此方程的求解和结构分析，判断其他外生变量变化对货币需求的动态影响。
1.1.1 差分方程求解：递归替代法差分方程求解就是将方程变量表示为外生变量及其初值的函数形式，可以通过以前的数据计算出方程变量的当前值。
由于方程结构对于每一个时间点都是成立的，因此可以将(1.1)表示为多个方程：0=t ：01100w y y ++=-φφ 1=t ：10101w y y ++=φφt t =：t t t w y y ++=-110φφ依次进行叠代可以得到：1011211010110101)()1()(w w y w w y y ++++=++++=--φφφφφφφφ0111122113121102)1(w w w y y φφφφφφφ++++++=-i ti i t t i it w y y ∑∑=-=++=011110φφφφ (1.2)上述表达式(1.2)便是差分方程(1.1)的解，可以通过代入方程进行验证。
时间序列分析习题解答第一章 P. 7 1.5 习题1.1 什么是时间序列？请收集几个生活中的观察值序列。
答：按照时间的顺序把随机事件变化发展的过程记录下来就构成一个时间序列。
例1：1820—1869年每年出现的太阳黑子数目的观察值；年份黑子数年份黑子数年份黑子数年份黑子数年份黑子数1820 16 1830 71 1840 63 1850 66 1860 96 1821 7 1831 48 1841 37 1851 64 1861 77 1822 4 1832 28 1842 24 1852 54 1862 59 1823 2 1833 8 1843 11 1853 39 1863 44 1824 8 1834 13 1844 15 1854 21 1864 47 1825 17 1835 57 1845 40 1855 7 1865 30 1826 36 1836 122 1846 62 1856 4 1866 16 1827 50 1837 138 1847 98 1857 23 1867 7 1828 62 1838 103 1848 124 1858 55 1868 37 1829 67 1839 86 1849 96 1859 94 1869 74 例2：北京市城镇居民1990—1999年每年的消费支出按照时间顺序记录下来，就构成了一个序列长度为10的消费支出时间序列（单位：亿元）。
1686，1925，2356，3027，3891，4874，5430，5796，6217，6796。
1.2 时域方法的特点是什么？答：时域方法特点：具有理论基础扎实，操作步骤规范，分析结果易于解释的优点，是时间序列分析的主流方法。
1.3 时域方法的发展轨迹是怎样的？答：时域方法的发展轨迹：一．基础阶段：1. G.U. Yule 1972年AR模型2. G.U.Walker 1931年 MA模型、ARMA模型二．核心阶段：G.E.P.Box和G.M.Jenkins1. 1970年，出版《Time Series Analysis Forecasting and Control》2. 提出ARIMA模型（Box-Jenkins模型）3. Box-Jenkins模型实际上主要运用于单变量、同方差场合的线性模型三．完善阶段：1.异方差场合：a.Robert F.Engle 1982年 ARCH模型b.Bollerslov 1985年 GARCH模型2.多变量场合：C.Granger 1987年提出了协整（co-integration）理论3.非线性场合：汤家豪等 1980年门限自回归模型1.4 在附录1中选择几个感兴趣的序列，创建数据集。
初计量经济学之时间序列分析1. 引言时间序列分析是计量经济学中的一个重要领域，研究的是时间序列数据的性质、模式和预测方法。
时间序列数据是按照时间顺序排列的一系列观测值，包括经济指标、股票价格、气象数据等。
时间序列分析可以帮助我们理解和预测经济现象的发展趋势，为政府和企业决策提供科学依据。
本文将介绍时间序列分析的基本概念、方法和应用。
首先，我们将介绍时间序列分析的基本步骤和基本假设。
然后，我们将介绍时间序列模型的常用类型，包括自回归模型（AR）、滑动平均模型（MA）和自回归滑动平均模型（ARMA）。
最后，我们将介绍时间序列的应用领域，包括经济预测、金融风险管理和气象预测。
2. 时间序列分析的基本步骤时间序列分析的基本步骤包括数据的收集和准备、数据的探索性分析、模型的选择和估计、模型的诊断和预测。
下面将对每个步骤进行详细介绍。
2.1 数据的收集和准备数据的收集和准备是时间序列分析的第一步。
我们需要收集时间序列数据，并进行数据清洗和预处理。
数据清洗包括删除缺失值、处理异常值和去除趋势。
数据预处理包括对数据进行平滑处理、差分和变换。
2.2 数据的探索性分析数据的探索性分析是时间序列分析的第二步。
我们需要对时间序列数据进行可视化和统计分析，以了解数据的基本性质和模式。
可视化方法包括绘制时间序列图、自相关图和偏自相关图。
统计分析方法包括计算统计指标、分析趋势、季节性和周期性。
2.3 模型的选择和估计模型的选择和估计是时间序列分析的第三步。
我们需要选择合适的时间序列模型，并进行参数估计。
常用的时间序列模型包括自回归模型（AR）、滑动平均模型（MA）、自回归滑动平均模型（ARMA）和季节性模型。
2.4 模型的诊断和预测模型的诊断和预测是时间序列分析的最后一步。
我们需要对模型进行诊断，检验模型的拟合程度和残差的平稳性、独立性和正态性。
然后，我们可以使用模型进行未来值的预测。
3. 时间序列模型时间序列模型是描述和预测时间序列数据的数学模型。
《时间序列分析》课程教学大纲课程编号：33330775课程名称：时间序列分析课程基本情况：1．学分：3 学时：51学时（课内学时：45 课内实验：6）2．课程性质：专业必修课3．适用专业：统计学适用对象：本科4.先修课程：概率论、数理统计、随机过程5．首选教材：王燕：《应用时间序列分析》，中国人民大学出版社，2008出版。
备选教材：王振龙等编著：《时间序列分析》，中国统计出版社，2000年。
6．考核形式：闭卷考试7．教学环境：多媒体教室及实验室一、教学目的与要求本课程是数理统计学的一个重要分支，先期需完成的课程有概率论、随机过程。
通过本课程的学习，使学生掌握时间序列数据的分析方法，包括时间序列简介、平稳时间序列分析、时间序列分解、非平稳序列的随机分析、多元时间序列分析。
利用Eviews软件进行本课程的实验教学。
二、教学内容及学时分配课程内容及学时分配表三、教学内容安排第一章时间序列分析简介【教学目的】1、了解时间序列的定义及常用分析方法；2、掌握时间序列的几个基本概念：随机过程、平稳随机过程、非平稳随机过程、自相关、记忆性。
【教学重点】时间序列的相关概念。
【教学难点】随机过程、系统自相关性。
【教学方法】课堂讲授【教学内容】第一节时间序列的定义第二节时间序列分析方法第三节时间序列分析软件EVIEWS简介第二章时间序列的预处理【教学目的】1、掌握平稳性检验的原理和方法；2、掌握纯随机性检验的原理和方法。
【教学重点】平稳时间序列的定义及统计性质。
【教学难点】时间序列的相关统计量。
【教学方法】课堂讲授【教学内容】第一节平稳性检验一、特征统计量二、平稳时间序列的定义三、平稳时间序列的统计性质四、平稳时间序列的意义五、平稳时间序列的检验第二节纯随机性检验一、纯随机序列的定义二、白噪声序列的定义三、纯随机性检验第三章平稳时间序列序列分析【教学目的】1、理解ARMA模型的定义及性质。
2、掌握平稳序列建模方法。
3、掌握平稳时间序列的预测【教学重点】平稳时间序列建模【教学难点】模型识别，参数估计，序列预测【教学方法】课堂讲授与上机实验【教学内容】第一节方法性工具一、差分运算二、延迟算子三、线性差分方程第二节 ARMA模型的性质一、AR模型二、MA模型三、ARMA模型第三节平稳序列建模一、建模步骤二、样本自相关系数与偏相关系数三、模型识别四、参数估计五、模型检验六、模型优化第四节序列预测一、线性预测函数二、预测方差最小原则三、线性最小方差预测的性质四、修正预测第四章非平稳序列的确定性分析【教学目的】1、理解时间序列的分解原理。
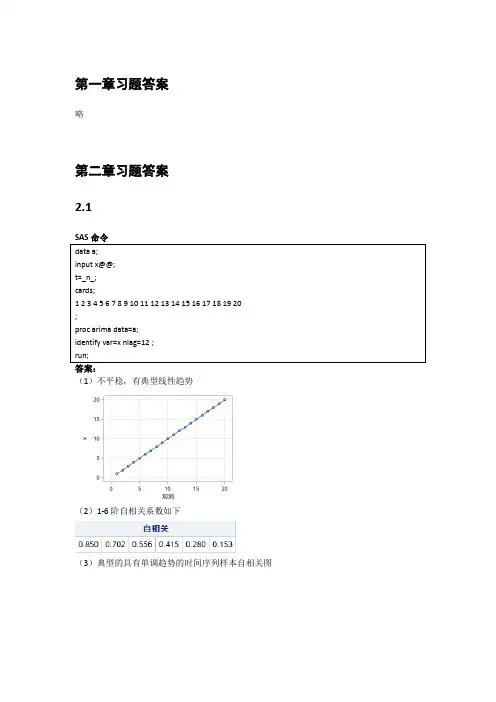
第一章习题答案略第二章习题答案2.1答案：（1）不平稳，有典型线性趋势（2）1-6阶自相关系数如下（3）典型的具有单调趋势的时间序列样本自相关图2.2答案：（1）不平稳（2）延迟1-24阶自相关系数（3）自相关图呈现典型的长期趋势与周期并存的特征2.3答案：（1）1-24阶自相关系数（2）平稳序列（3）非白噪声序列2.4计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05，所以该序列为纯随机序列。
2.5答案（1）绘制时序图与自相关图（2）序列时序图显示出典型的周期特征，该序列非平稳（3）该序列为非白噪声序列2.6答案（1）如果是进行平稳性图识别，该序列自相关图呈现一定的趋势序列特征，可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别，该序列带漂移项的0阶滞后P值小于0.05，可以视为平稳非白噪声序列（2）差分后序列为平稳非白噪声序列2.7答案（1）时序图和自相关图显示该序列有趋势特征，所以图识别为非平稳序列。
（2）单位根检验显示带漂移项0阶延迟的P值小于0.05，所以基于adf检验可以认为该序列平稳（3）如果使用adf检验结果，认为该序列平稳，则白噪声检验显示该序列为非白噪声序列如果使用图识别认为该序列非平稳，那么一阶差分后序列为平稳非白噪声序列2.8答案（1）时序图和自相关图都显示典型的趋势序列特征（2）单位根检验显示该序列可以认为是平稳序列（带漂移项一阶滞后P值小于0.05）（3）一阶差分后序列平稳第三章习题答案 3.10101()0110.7t E x φφ===--（） 221112() 1.96110.7t Var x φ===--（） 22213=0.70.49ρφ==（）12122221110.490.7=0110.71ρρρφρρ-==-（4） 3.21111222211212(2)7=0.515111=0.30.515AR φφφρφφφρφρφφφ⎧⎧⎧=⎪=⎪⎪⎪--⇒⇒⎨⎨⎨⎪⎪⎪=+=+⎩⎩⎪⎩模型有：,2115φ=3.312012(1)(10.5)(10.3)0.80.15()01t t t t t tt B B x x x x E x εεφφφ----=⇔=-+==--,22121212()(1)(1)(1)10.15=(10.15)(10.80.15)(10.80.15)1.98t Var x φφφφφφ-=+--+-+--+++=（）1122112312210.83=0.70110.150.80.70.150.410.80.410.150.70.22φρφρφρφρφρφρ==-+=+=⨯-==+=⨯-⨯=（） 1112223340.70.15=0φρφφφ====-（）3.41211110011AR c c c c c ⎧<-<<⎧⎪⇒⇒-<<⎨⎨<±<⎪⎩⎩（） （）模型的平稳条件是 1121,21,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩（） 3.5证明:该序列的特征方程为：320c c λλλ--+=，解该特征方程得三个特征根：11λ=，2λ=3λ=无论c 取什么值，该方程都有一个特征根在单位圆上，所以该序列一定是非平稳序列。
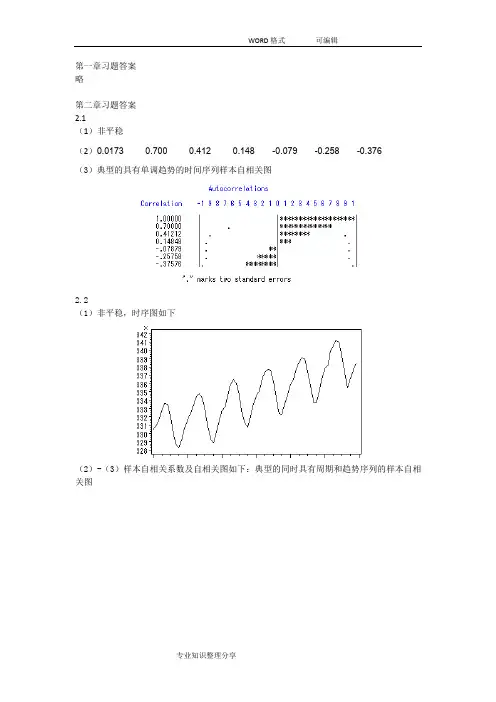
第一章习题答案略第二章习题答案2.1（1）非平稳（2）0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376（3）典型的具有单调趋势的时间序列样本自相关图2.2（1）非平稳，时序图如下（2）-（3）样本自相关系数及自相关图如下：典型的同时具有周期和趋势序列的样本自相关图2.3（1）自相关系数为：0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118（2）平稳序列（3）白噪声序列2.4，序列LB=4.83，LB统计量对应的分位点为0.9634，P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5（1）时序图与样本自相关图如下（2） 非平稳 （3）非纯随机 2.6（1）平稳，非纯随机序列（拟合模型参考：ARMA(1,2)） （2）差分序列平稳，非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为：32--c 0c λλλ+=，解该特征方程得三个特征根：11λ=，2c λ=3c λ=-无论c 取什么值，该方程都有一个特征根在单位圆上，所以该序列一定是非平稳序列。
