当前位置：文档之家 › 最新(复数的加法和减法)1pt

最新(复数的加法和减法)1pt

  • 格式：ppt
  • 大小：359.50 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

复数的加法和减法课件1(PPT)5-4

复数的加法和减法课件1(PPT)5-4
复习引入
ቤተ መጻሕፍቲ ባይዱ
(1)复数加法法则及其几何意义 y (a+bi)+(c+di)=(a+c)+(b+d)i
Z2
Z
Z1
o
x
(2)复数减法法则及其几何意义. y (a+bi)-(c+di)=(a-c)+(b-d)i Z2
Z1
x o
让更多的孩子得到更好的教育
青黑色：～发。②昏暗。 【灿】（燦）光彩耀眼：～然｜～若云锦｜黄～～的菜花。 【灿烂】形光彩鲜明耀眼：星光～｜～辉煌◇～的笑容。 【灿亮】形 光亮耀眼：明光～。 【灿然】形形容明亮：阳光～｜～炫目｜～一新。 【掺】（摻）古代一种鼓曲：渔阳～（就是渔阳三挝）。 【孱】义同“孱”（）， 用于“孱头”。 【孱头】?〈方〉名软弱无；304不锈钢板 304不锈钢板；能的人（骂人的话）。 【粲】〈书〉鲜明；美好：～ 然｜云轻星～。 【粲然】〈书〉形①形容鲜明发光：星光～。②形容显著明白：～可见。③笑时露出牙齿的样子：～一笑。 【璨】①美玉。②同“粲”。 【仓】（倉）①名仓房；仓库：粮食满～。②指仓位?：补～｜减～。③（）名姓。 【仓储】动用仓库储存：～超市｜～物资。 【仓促】形匆忙：～应战｜ 时间～，来不及细说了。也作仓猝。 【仓猝】同“仓促”。 【仓房】名储藏粮食或其他物资的房屋。 【仓庚】同“鸧鹒”。 【仓皇】形匆忙而慌张：～失
【苍凉】形凄凉：月色～。 【苍龙】名①二十八宿中东方七宿的统称。也叫青龙。参看页〖二十八宿〗。②古代传说中的一种凶神恶煞。现在有时用来比
北京四中龙门网络教育技术有限公司 Beijing Etiantian Net Educational Technology Co.,Ltd
例2. 根据复数的意义和向量表示,求复平面 内的圆的方程.

复数的基本运算公式

复数的基本运算公式

复数的基本运算公式复数是由实数和虚数构成的数学概念，在高中数学中被广泛应用。

复数的运算是高中数学的重要内容之一，其基本运算公式包括加法、减法、乘法和除法。

本文将详细介绍这些基本运算公式，并给出相应的实例，以帮助读者更好地理解和掌握复数的基本运算。

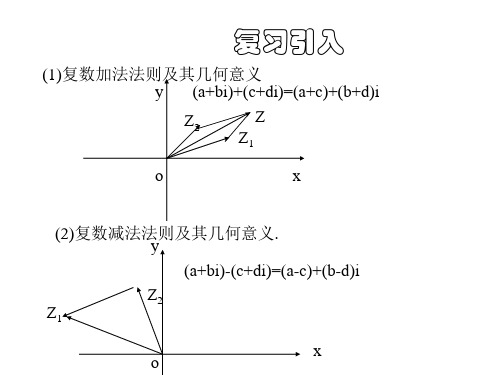
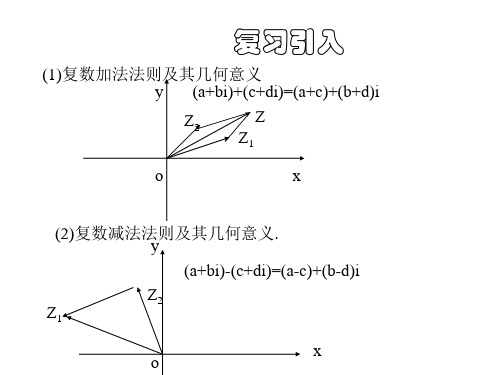
一、复数的加法复数的加法是指将两个复数相加得到一个新的复数，其基本公式如下：(a+bi) + (c+di) = (a+c) + (b+d)i其中，a、b、c、d均为实数，i为虚数单位，表示-1的平方根。

这个公式的实现方法相当简单，只需要将两个复数的实部（即a和c）相加，并将虚部（即b和d）相加即可。

例如，将复数（3+2i）和（4-5i）相加，运用上述公式，可以得到结果为（7-3i）。

二、复数的减法复数的减法与加法类似，只是将两个复数相减，其基本公式如下：(a+bi) - (c+di) = (a-c) + (b-d)i同样，实现方法也很简单，只需要将两个复数的实部相减，并将虚部相减即可。

举个例子，将复数（6-5i）减去（3+2i），使用上述公式，可以得到结果为（3-7i）。

三、复数的乘法复数的乘法是将两个复数相乘得到一个新的复数，其基本公式如下：(a+bi)×(c+di) = (ac-bd)+(ad+bc)i其中，a、b、c、d均为实数，i为虚数单位。

推导这个公式较为复杂，因此我们直接给出一个例子：将复数（2+3i）和（4-5i）相乘，运用上述公式，可以得到结果为（23-2i）。

四、复数的除法复数的除法是将一个复数除以另一个复数得到一个新的复数，其基本公式如下：(a+bi)÷(c+di) = [(ac+bd)+(bc-ad)i]÷(c²+d²)需要注意的是，作为除数的复数不能为0。

另外，需要将分子和分母同时乘以（c-di），再根据公式进行简化。

例如，将复数（1+2i）除以（3+4i），运用上述公式，可以得到结果为（11-2i）÷25。

7.2.1 复数的加、减运算及其几何意义课件ppt

7.2.1 复数的加、减运算及其几何意义课件ppt
出向量, 对应的复数,通过平面向量的数量积求出向量, 的夹角的
正弦值,进而求出△AOB 的面积.
解 (1)因为四边形 ABCD 是平行四边形,
所以 = + ,于是 = − ,
而(1+4i)-(3+2i)=-2+2i,即对应的复数是-2+2i.
(2)因为 = − ,而(3+2i)-(-2+2i)=5,
微练习
(1)若z1=-2+4i,z2=3-2i,则z1+z2=
(2)(5-5i)-3i=
.
答案 (1)1+2i (2)5-8i
解析(1)z1+z2=(-2+4i)+(3-2i)=1+2i.
(2)(5-5i)-3i=5-8i.
.
知识点二、复数加法的几何意义
设1 , 2 分别与复数 a+bi,c+di(a,b,c,d∈R)对应,则1 =(a,b),2 =(c,d).
这说明两个向量1 与2 的差就是与复数(a-c)+(b-d)i 对应的向量.因此,复
数的减法可以按照向量的减法来进行,这就是复数减法的几何意义.
微练习
若在复平面上的平行四边形 ABCD 中, 对应的复数为 6+8i,对应的复数
为-4+6i,则对应的复数是
.
答案 -1-7i
解析由复数加法、减法的几何意义可得 =
因此 cos∠AOB=- 17 ,故 sin∠AOB= 17 ,
1
1
17 5 4 17 5
5
故 S△AOB=2 ||||sin∠AOB=2 × 2 × 2 × 17 = 2,即△AOB 面积为2.

复数的加法和减法课件1(PPT)5-1

复数的加法和减法课件1(PPT)5-1
地轴，从地球上看，它的位置几乎不变，可以靠它来辨别方向。由于岁差，北极星并不是永远不变的某一颗星，现在是小熊座α星，到公元年将是织女星。参 看〖北斗星〗。 【北极熊】名哺乳动物，毛白色带黄，长而稠密，鼻子和爪黑色。生活在北寒带，善于游泳。也叫白熊。 【时间】ī我国的标准时。以东经 °子午线为标准的时刻，即所在时区的标准时刻。 【猿人】ī中国猿人的一种，生活在距今约—多万年以前。年在周口店龙骨山山洞发现了第一颗牙齿化石， 年发现了第一个完整的头骨化石。也叫人。 【北面】?（～儿）名方位词。北边。 【北欧】名欧洲北部，包括丹麦、挪威、瑞典、芬兰和冰岛等国。 【北齐】 名北朝之一，公元—，高洋所建。参看页〖南北朝〗。 【北曲】名①宋元以来北方诸宫调、散曲、戏曲所用的各种曲调的统称，调子豪壮朴实。②元代流行 于北方的戏曲。参看页〖杂剧〗。 【北山羊】名哺乳动物，外形似山羊而大，雄雌都有角，雄的角大，向后弯曲，生活在高山地带。也叫羱（）羊。 【北上】 动我国古代以北为上，后来把去本地以北的某地叫北上（跟“南下”相对）：近日将自～。 【北宋】名朝代，公元—，自太祖（赵匡胤）建隆元年起，到钦 宗（赵桓）靖康二年止。建都汴京（今河南开封）。 【北纬】名赤道以北的纬度或纬线。参看页〖纬度〗、页〖纬线〗。 【北魏】名北朝之一，公元—，鲜 卑人拓跋珪所建，后来分裂为东魏和西魏。参看页〖南北朝〗。 【北温带】名北半球的温带，在北极圈与北回归线之间。参看页〖温带〗。 【北洋】名清未 指奉天（辽宁）、直隶（河北）、山东沿海地区。特设北洋通商大臣，由直隶总督兼任。 【北洋军阀】民国初年（—）代表北方封建势力的军阀集团，是清 末北洋派势力的延续。最初的首领是袁世凯，袁死后分成几个派系，在帝国主义的支持下先后控制了当时的政府，镇压力量，出卖国家主权，连年进行内战。 【北野】名姓。 【北周】名北朝之一，公元—，鲜卑人宇文觉所建。参看页〖南北朝〗。 【贝】（貝）①名有壳的软体动物的统称。如蛤蜊、蚌、鲍鱼、田

《复数的四则运算》复数PPT(复数的加、减运算及其几何意义)

《复数的四则运算》复数PPT(复数的加、减运算及其几何意义)

手抄报：www.1ppt.c om /shouc ha oba o/
P P T课件：www.1ppt.c om /ke j ia n/
语文课件：/kejian/y uwen/ 数学课件：/kejian/shuxue/
英语课件：/kejian/y ingy u/ 美术课件：/kejian/meishu/
(1)两个虚数的和或差可能是实数．(√ PPT模板：/moban/
P P T素材：www.1ppt.c om /suc a i/
P P T背景：www.1ppt.c om /be ij ing/
P P T图表：www.1ppt.c om /tubia o/
P P T下载：www.1ppt.c om /xia za i/
化学课件：/kejian/huaxue/ 生物课件：/kejian/shengwu/
地理课件：www.1ppt.c om /ke j ia n/dili/
历史课件：www.1ppt.c om /ke j ia n/lishi/
问题导学
预习教材 P75－P77 的内容，思考以下问题： 1．复数的加、减法运算法则是什么？运算律有哪些？ 2．复数的加、减法的几何意义是什么？
试卷下载：www.1ppt.c om /shiti/
教案下载：www.1ppt.c om /j ia oa n/
手抄报：www.1ppt.c om /shouc ha oba o/
P P T课件：www.1ppt.c om /ke j ia n/

语文课件：/kejian/y uwen/ 数学课件：/kejian/shuxue/
P P T课件：www.1ppt.c om /ke j ia n/
语文课件：/kejian/y uwen/ 数学课件：/kejian/shuxue/

复数的加法与减法PPT优秀课件

复数的加法与减法PPT优秀课件

注意到 i 2 1 ，虚数单位 i 可以和实数进行运 算且运算律仍成立，所以复数的加、减、乘运算我 们已经是自然而然地在进行着， 只要把这些零散的 操作整理成法则即可了！
1.复数加、减法的运算法则： 已知两复数z1=a+bi, z2=c+di（a,b,c,d是实数） (1)加法法则：z1+z2=(a+c)+(b+d)i; (2)减法法则：z1-z2=(a-c)+(b-d)i.
3.2.1《复数代数形式的的 四则运算-复数的加法与减法》
教学目标
• 掌握复数的加法与减法的运算及几何意义 • 教学重点： • 掌握复数的加法与减法的运算及几何意义
复数的四则运算(一)
问题引入
复数的运算 法则
复数加减运算 巩固练习 的几何意义
作业:自由安排
复数的四则运算(一)
我们知道实数有加、减、乘等运算，且有运算律： ab ba ab ba (a b) c a (b c) (ab)c a(bc) a(b c) ab ac 那么复数应怎样进行加、减、乘运算呢？你认为应 怎样定义复数的加、减、乘运算呢？运算律仍成立吗？
2.复数的乘法法则：
2
说明:(1)两个复数的积仍然是一个复数； (2)复数的乘法与多项式的乘法是类似的，只是在 运算过程中把 i 2 换成－1，然后实、虚部分别合并. (3)易知复数的乘法满足交换律、结合律以及分配律
即对于任何z1 , z2 ,z3 ∈C,有
z z z z z z ) z z z z ) , 1 2 2 1 , ( 1 2 3 1( 2 3 zz (2 z ) z z z z . 1 3 12 13
y

复数运算公式大全(二)2024

复数运算公式大全（二）引言概述：本文旨在介绍复数运算的一系列公式。

复数是由实部和虚部构成的数，可以用于解决许多实际问题，包括电学、物理学和工程学中的许多应用。

通过掌握这些公式，读者将能够更好地理解和应用复数。

正文：I. 复数的加法和减法1. 复数的加法公式：利用实部和虚部的加法规则，将两个复数相加得到一个新的复数。

- 实部相加、虚部相加2. 复数的减法公式：通过复数的加法公式，将减法转换为加法问题。

- 实部相减、虚部相减II. 复数的乘法和除法1. 复数的乘法公式：使用分配律和复数的乘法规则，将两个复数相乘得到一个新的复数。

- 实部乘积减去虚部乘积2. 复数的除法公式：通过将复数相乘的结果除以除数的模长平方，得到一个新的复数作为商。

- 模长平方的乘法逆元III. 复数的模长和共轭1. 复数的模长公式：计算一个复数的模长，即复数到原点的距离。

- 利用勾股定理计算2. 复数的共轭公式：将复数的虚部取相反数，得到一个新的复数。

- 修改虚部的符号IV. 复数的幂和根1. 复数的幂公式：根据欧拉公式和指数的性质，计算复数的任意幂。

- 欧拉公式的应用2. 复数的根公式：求解复数的根，即找到满足幂次方等于给定复数的特定复数。

- 公式和数值计算的结合V. 特殊复数运算1. 复数的逆运算：求解复数的倒数，满足乘积为1的复数。

- 模长平方的倒数2. 复数的幅角运算：计算复数的幅角，即与实轴的夹角。

- 反三角函数和辅助角的应用3. 复数的极坐标形式与直角坐标形式的转换：将复数在直角坐标系和极坐标系之间进行转换。

- 利用三角函数的关系式总结：本文详细介绍了复数运算的一系列公式，包括加法、减法、乘法、除法、模长、共轭、幂、根、逆运算、幅角和坐标系转换。

这些公式是理解和应用复数的基础。

通过掌握这些公式，读者将能够更好地处理涉及复数的问题，并在电学、物理学和工程学等领域中应用复数。

复数的加减乘除运算

复数的加减乘除运算复数在数学中是一种重要的概念，它由实数和虚数部分组成。

复数的加减乘除运算是我们在数学学习中经常遇到的问题。

本文将详细介绍复数的加减乘除运算方法和规则。

一、复数的表示形式复数通常可以表示为 a + bi 的形式，其中 a 为实数部分，bi 为虚数部分，i 为虚数单位，满足 i² = -1。

在这种表示形式下，a 和 b 分别称为复数的实部和虚部。

二、复数的加法运算复数的加法运算遵循实部相加，虚部相加的原则。

具体计算公式如下：(a + bi) + (c + di) = (a + c) + (b + d)i例如，计算 (2 + 3i) + (4 + 5i)，按照上述原则进行计算，得到结果为6 + 8i。

三、复数的减法运算复数的减法运算同样遵循实部相减，虚部相减的原则。

具体计算公式如下：(a + bi) - (c + di) = (a - c) + (b - d)i例如，计算 (5 + 6i) - (2 + 3i)，按照上述原则进行计算，得到结果为3 + 3i。

四、复数的乘法运算复数的乘法运算通过展开计算实现。

具体计算公式如下：(a + bi) * (c + di) = (ac - bd) + (ad + bc)i例如，计算 (2 + 3i) * (4 + 5i)，按照上述公式进行计算，得到结果为-7 + 22i。

五、复数的除法运算复数的除法运算需要借助共轭复数。

共轭复数的定义为：如果 z = a + bi，则其共轭复数为z = a - bi。

复数除法的计算公式如下：(a + bi) / (c + di) = [(ac + bd) + (bc - ad)i] / (c² + d²)例如，计算 (8 + 6i) / (2 + 3i)，按照上述公式进行计算，得到结果为2 + 1i。

综上所述，复数的加减乘除运算都有相应的计算规则和公式，我们可以根据这些规则和公式进行运算。

复数的加法和减法(上课用)ppt


OZ1=(a,b) OZ2=(c,d)
z z 1 z2 a c b d i
uuur uuur uuuur y
Z(a+c,b+d)
OZ = OZ1 + OZ2 = (a,b) + (c,d )
Z2(c,d)
= (a + c,b + d )
Z1(a,b)
结论：复数的加法o可以按照向量的加法来进行 x
-
13
1.已知复数z对应点A,说明下列各式所 表示的几何意义.
(1)|z－(1+2i)| 点Z到点(1,2)的距离
(2)|z+(1+2i)|点Z到点(－1, －2)的
距离
(3)|z+2i| 点Z到点(0, －2)的距离
(4)|z－1| 点A到点(1,0)的距离
-
14
2. 设复数z=x+yi,(x,y∈R),在下列
3+x=5, ∴ 2-y=-6.
x=2 ∴
y=8
∴z1 - z2 = (2+2i) - (3-8i) = -1+10i
-
8
例4、设Z , Z ∈C，求证：
12
Z +Z
12
=
Z 1+
Z
2
，Z -Z=
12
Z- 1
Z
2
证明：设Z=1 a1+b1i ， Z2= a2+b2i (a1 , a2 , b1 , b2) ∈R ，则
(a+bi)-(c+di)=(a+bi)+(-c-di)
=(a-c)+(b-d)i
两个复数相减就是把实部与实部、虚部与虚部

复数的加法与减法ppt课件


15
例 ： 若 复 数z对 应 点A， 说 出 下 列 复 数 模 的 几何 意 义 ： (1) | z 1 | (2) | z 2 i | (3) | z 2i | (4) | z 1 i | (1)表示A到点(1,0)的距离 (2)表示A到点(2,1)的距离 (3)表示A到点(0,2)的距离 (4)表示A到点(1,1)的距离
Z2(c,d)
Z1(a,b)
o
x
结论：复数的加法可以按照向量的加法来进行,复数的
和对应向量的和。
5
2.复数减法运算的几何意义?
复数z2－z1
向量Z1Z2
符合 向量
y
Z2(c,d)
减法
的三 角形
Z1(a,b)
法则.
x
o
结论：复数的差Z2－Z 1 与连接两个向量终点并指向被
减数的向量对应.
6
归纳总结
3+x=5, ∴ 2-y=-6.
x=2
∴ y=8
∴z1 - z2 = (2+2i) - (3-8i) = -1+10i
8
几何意义运用
• 例3 已知OA,OB对应复数是3 2i,2 i,求向 量 AB对应的复数.
• 变式1 已知复平面内一平行四边形AOBC顶点A,O,B 对应复数是 -3+2i, 0, 2+i ，求点C对应的复数.
例：若复数z满足 | z 3 4i | 1,则z所对应点的集合是 什么图形？
表示以(3,4)为圆心，1为半径的圆
16
r
２、如果复数ｚ对应着复平面上的点Ｚ(ｘ，ｙ)， 一些常用曲线的复数形式的方程为：
(1)方程 z z0 r 表示以z0为圆心,r为半径的圆;
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
思考？ 复数是否有减法？如何理解复数的减法？
复数的减法规定是加法的逆运算，即把满足
（c+di）+（x+yi）= a+bi 的复数x+yi 叫做复数 a+bi减去复数c+di的差，记作 （a+bi） － （c+di）
请同两个学复们数推相导减复就数是把的实减部法与法实则部。、虚部与虚部分别相减，
即
事实上，由复数相等的定义，有： c+x=a， d+y=b
拓展延伸 思考？
yZ P
O
x
巩固提高
1 .(2+4i)+(3-4i) =(2+3)+(4-4)i =5 2. 5-(3+2i) =(5-3)+(0-2)i =2-2i 3.(-3-4i)+(2+i)-(1-5i)=(-3+2-1)+(-4+1+5)i = -2+2i 4.(2-i)-(2+3i)+4i =(2-2+0)+(-1-3+4)i =0 5.(3+5i)+(3-4i) =(3+3)+(5-4)i=6+i 6.(-3+2i)-(4-5i) =(-3-4)+[2-(-5)]i= -7+7i 7.(5-6i)+(-2-2i)-(3+3i)=(5-2-3)+(-6-2-3)i= -11i
三、课堂练习 1、计算：（1）(－ 3 －4i)+(2+i) －(1 －5i)=__－_2_+_2_i_____
（2） ( 3 －2i) －(2+i) －(___－_9_i___)=1+6i 2、已知x∈R，y为纯虚数，且（2x －1)+i=y －(3 －y)i 则x=_－__23____ y=__4_i____ 分3的4分 －、 、析点由1析已复)：关复+：知平i先=于数依(复 面a求虚相题数 内－出轴等意关Z3Z对得)1设i1=于++称y－Za原=i2点22a2=+点=ix2的i（－，对－－复aa1Zi称+∈，=2数(=－的R所a4。a）－两以－，23点Zi)，则i1对+试Z原应2求在式x的=Z复变－复1+平为23数Z面：2为对内（Z应1对2，x应 的Z2点，是且(满2，足－Z11+)，i=其Z2a关－－2于3，=虚求1 轴Z的1和对Z称2。点y为=(4i－2， －1)， 故分所析求：复 依数 题是 意设－2Z－1=i x+yi（x，y∈R）则Z2= －x －yi， 由Z1+i=Z2 －2得：x+(y+1)i= －(x －2)+(－y)i，由复数相 等可求得x= －1，y= －1/2
3. 复数的几何意义是什么？
一一对应
复数z a bi
平面向量 O Z
或点 z（a,b）
类比实数的运算法则能否得到复数的
运算法则？
认识新知
1、复数的加法法则：设Z1=a+bi，Z2=c+di (a、b、c、d∈R)是任意两个复数，那么它 们的和：
（a+bi)+(c+di)=(a+c)+(b+d)i
点评:（1）复数的加法运算法则是一种规定。当 b=0，d=0时与实数加法法则保持一致 （2）很明显，两个复数的和仍 然是一个复数。 对于复数的加法可以推广到多个复数相加的情 形。
练习 课堂小结
1．复数的加法与减法运算法则； 2．加法、减法的几何意义．
作业： p112习题3.2 1, 2，3
此课件下载可自行编辑修改，仅供参考！ 感谢您的支持，我们努力做得更好！谢谢
数。
深入探究？
类比复数加法的几何意义，请指出复数 减法的几何意义？
复数减法的几何意义：
O Z 1 O Z 2 Z 2 Z 1
y Z1 O
Z2 x
学 以致用 讲解例题
例1 计算 (5－6i) ＋(－ 2 － i) －(3 ＋ 4i) 解： (5－6i)＋(－ 2 － i) －(3 ＋ 4i) ＝(5－2 －3) ＋ ( －6 － 1 － 4 ) i ＝11 i
运算律
探究? 复数的加法满足交换律，结合律吗？
证 复：数设的Z加1=a法1+满b1i足，交Z2=换a2律+b、2i，结Z合3=a律3+，b3i即(a对1，任a2，
a意3，Zb1∈1，Cb，2，Zb23∈∈RC)，Z3∈C
则Z1+Z2=（aZ1+1+a2Z)+2=(bZ1+2+b2Z)i1，Z2+Z1=（a2+a1)+(b2+b1)i
显然
Z1+Z2=Z2+Z1
同理可(得Z1+Z2)(+ZZ1ư+ZZ1+3)(Z2+Z3)
点评：实数加法运算的交换律、结合律在复数 集C中依然成立。
思维的提升
探究？复数与复平面内的向量有一一的对应关系。我们讨论过
向量加法的几何意义，你能由此出发讨论复数加法的几何意义吗？
由此( a ，b 得i )( c x=ad i －) c，( a c y) =b( b － dd ) i
所以 x+yi=(a － c)+(b － d)i
即：（a+bi） － （c+di）= (a － c)+(b － d)i 点评：根据复数相等的定义，我们可以得出复数
的减法法则，且知两个复数的差是唯一确定的复
设 O Z 1 及 O Z 2 分别与复数 a bi 及复数 c di对应，则 OZ1, (a,b)
OZ2 (c,d)
OZ OZ1 OZ2 (a,b) (c,d )
y Z2(c,d)
O
Z
Z1(a,b) x
(a c,b d )
∴向量 O Z 就是与复数 (a c) (b d)i 对应的向量.
深入探究
(复数的加法和减法)1pt
教学重点
复数的加减法的运算法则及其
几何意义。 教学难点
复数的加减法的运算法则的几何 意义理解与运用。
知识回顾
1、复数的概念：形如a_+__b_i _(_a_，__b_∈__R_)_的数叫做复 数，a，b分别叫做它的_实__部__和__虚__部____。
2_a_、1_=_复a_2_数，__Zb_11=_=_ab_12+_b。1i与Z2=a2+b2i 相等的充要条件是
8.设z1= x+2i,z2= 3-yi(x,y∈R),且z1+z2 = 5 - 6i,求
z1-z2
解：∵z1=x+2i，z2=3-yi，z1+z2=5-6i ∴(3+x)+(2-y)i=5-6i
3+x=5, ∴ 2-y=-6.
x=2
∴ y=8
∴z1 - z2 = (2+2i) - (3-8i) = -1+10i