数学实验1

B1=[b11 b12 b13 b14 ;b21 b22 b23 b24; b31 b32 b33 b34]
运行
17
矩阵的运算(矩阵的加减、数乘、乘积)
C=A1+B1 D=A1-B1 syms c, cA=c*A1 A2=A1(:,1:3), B1 G=A2*B1
18
矩阵的运算(矩阵的加减、数乘、乘积)
求解方程组Ax=b x=A\b 若A为可逆方阵, 输出原方程的解x; 若A为nxm(n>m)阵, 且A’A可逆,输出
原方程的最小二乘解x.
21
矩阵的运算(求解线性方程组)
求矩阵方程：
设A、B满足关系式：AB＝2B+A,求B。 其中A=[3 0 1; 1 1 0; 0 1 4]。
取出A的1、3行和1、3列的交叉处元素 构成新矩阵A1
程序
A=[1 0 1 1 2;0 1 -1 2 3;

3 0 5 1 0;2 3 1 2 1],
vr=[1, 3];vc=[1, 3];
A1=A(vr, vc)
观察结果
26
分块矩阵（矩阵的标识）
将A分为四块，并把它们赋值到矩阵B 中，观察运行后的结果。
3
2
2

35 20 60 45
, B 10
15
50
40

20 12 45 20
将 表 格 写 成 矩 阵 形 式
6
计算
输入下面Matlab指令 A=[4 2 3;1 3 2;1 3 3;3 2 2], B=[35 20 60 45;10 15 50 40;20

3 0 5 1 0;2 3 1 2 1]

MATLAB数学实验报告1Matlab数学实验报告⼀、实验⽬的通过以下四组实验,熟悉MATLAB的编程技巧,学会运⽤MATLAB的⼀些主要功能、命令，通过建⽴数学模型解决理论或实际问题。

了解诸如分岔、混沌等概念、学会建⽴Malthu模型和Logistic 模型、懂得最⼩⼆乘法、线性规划等基本思想。

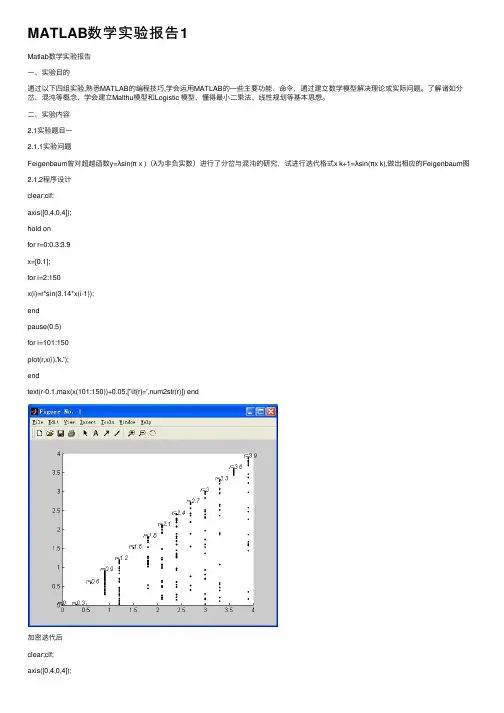
⼆、实验内容2.1实验题⽬⼀2.1.1实验问题Feigenbaum曾对超越函数y=λsin(πｘ)（λ为⾮负实数）进⾏了分岔与混沌的研究，试进⾏迭代格式x k+1=λsin(πx k),做出相应的Feigenbaum图2.1.2程序设计clear;clf;axis([0,4,0,4]);hold onfor r=0:0.3:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.5)for i=101:150plot(r,x(i),'k.');endtext(r-0.1,max(x(101:150))+0.05,['\it{r}=',num2str(r)]) end加密迭代后clear;clf;axis([0,4,0,4]);hold onfor r=0:0.005:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.1)for i=101:150plot(r,x(i),'k.');endend运⾏后得到Feigenbaum图2.2实验题⽬⼆2.2.1实验问题某农夫有⼀个半径10⽶的圆形⽜栏，长满了草。

他要将⼀头⽜拴在⽜栏边界的桩栏上，但只让⽜吃到⼀半草，问拴⽜⿐⼦的绳⼦应为多长？2.2.2问题分析如图所⽰，E为圆ABD的圆⼼，AB为拴⽜的绳⼦，圆ABD为草场，区域ABCD为⽜能到达的区域。

问题要求区域ABCD等于圆ABC的⼀半，可以设BC等于x,只要求出∠a和∠b就能求出所求⾯积。

（1）参数方程：z=2^2^/2^2^sin y x y x ++（-8<=x<=8,-8<=y<=8) （2）程序：[X,Y]=meshgrid(-8::8);r=sqrt(x.^2+y.^2)+eps;Z=sin(r)./r;Mesh(x,y,z)Axis square(3)程序的输出结果：3：球面,椭球面,双叶双曲面,单叶双曲面1球面: (4):参数方程：⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *R z R y R x 0π<=θ<2* 0<=ϕ<π (5)程序：u=[0:pi/60:2*pi];v=[0:pi/60:pi];[U,V]=meshgrid(u,v);R=3;X=R*sin(v).*cos(u);Y=R*sin(v).*sin(u);Z=R*cos(v);Surf(x,y,z);axis equal;(3)程序输出结果：2椭球面： （1）参数方程：⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *c z b y a x 0<=θ<2*π 0<=ϕ<=π （2）程序：ezsurf(‘3*sin(u)*cos(v) ,’3*sin(u)*sin(v)’,’1*cos(u)’,[0,pi,0,2*pi]);(3)程序的输出结果：3单叶双曲面： （1）参数方程：⎪⎩⎪⎨⎧===ϕθϕθϕtan sin *sec *cos *sec *z a y a x 0<=θ<2*π -π/2<ϕ<π/2 （2）程序：ezsurf(‘3*sec(u)*cos(v),’3*sec(u)*sin(v)’,’5*tan(u)’,[-pi/2,pi/2,0,2*pi]);axis auto（3）输出程序结果：4双叶双曲面： （1）参数方程：⎪⎩⎪⎨⎧===ϕθϕθϕsec *sin *tan *cos *tan *c z b y a x 0<=θ<2*π -π<ϕ<3*π/2，ϕ≠π/2（2）程序：ezsurf(‘3*tan(u)*cos(v)’,’3*tan(u)*sin(v)’,’5*sec(u)’,[-pi/2,3*pi/2,0,2*pi]);axis auto（4） （3）输出程序结果：抛物螺线： （1）参数方程：⎪⎩⎪⎨⎧===2^*sin **cos **t c z t t b y t t a x 0<T<+∞ （2）程序：ezplot3(‘2*t*cos(t)’,’2*t*sin(t)’,’t.^2/3’,[0,50]);（3）输出程序结果：（5）马鞍面： （1）参数方程：z=x^2/9-y^2/4 （-25<=x<=25,-25<=y<=25)（2）程序：[X,Y]=meshgrid(-25:1:25);Z=X.^2/9-Y.^2/4;Surf(X,Y,Z)Title(‘马鞍面’)grid off（3）输出程序结果：（6）黎曼函数：（1）程序：n=100;x=[];y=[];k=1;for q=2:nfor p=1:q-1if gcd(q,p)==1 %利用函数gcd(m,n)可求m和n的最大公约数x(k)=p/q;y(k)=1/q;k=k+1;endendendplot(x,y,’.b’); axis([0,1,0,1])（2）程序输出结果：。

（4）评判结束后，求出各选手的平均分，按平均分从低到高排序，依次确定本次评比的名次，即平均分最低者获得资助最高，依次类推。
d1100101010011000过河的方式有两种过河次数为奇数时船从此岸划向彼岸过河次数为偶数时船从彼岸划向此岸所以则状态ks随决策kd变化的规律为??kdkksks11????因此设计安全过河方案归结为求决策序列21ddddn??使状态ssk?按状态转移律由初始状态??11111?s经n步达到??00001??ns
我们将人，猫，鸡，米在岸上的情况，依次用四维向量S表示，即S（人,猫,鸡,米），并将这些向量称为状态，则第k次渡河前的状态记为 。
当一物在此岸时，相应分量记为1，在彼岸时记为0。例如（1，1，1，1）表示它们都在此岸，（0，1，1，0）表示猫和鸡在此岸，人和米在彼岸。由于问题中的限制条件，有些状态是允许的，有些状态是不允许的。安全渡河条件下的状态称为允许状态。对本问题而言，允许状态集合为：
(1,0,0,0)
(1,0,0,1)
(1,0,1,0)
(1,1,0,0)
(1,0,0,0)
(1,0,1,0)
1
2
3
4
5
6
7
8
(1,1,1,1)
(0,1,0,1)
(1,1,0,1)
(0,0,0,1)
(1,1,0,1)
(0,0,1,0)
(1,0,1,0)
(0,0,0,0)
(1,0,1,0)
(1,0,0,0)
（2）甲乙两站之间有汽车想通，每隔10分钟甲乙两站相互发一趟车，但发车时刻不一定相同。甲乙两站之间有一中间站丙，某人每天在随机时刻到达丙站，并搭乘最先经过丙站的那趟车，结果发现100天中约有90天到达甲站，大约10天到达乙站。问开往甲乙两站的汽车经过两站的时刻表是如何安排的？

>> x=1.5951;eval(yxx)
ans =
18.3287
函数的单调区间为：
(1)单调递增区间:-2<x<-1.5326 -0.7315<x<0以及1.5951<x<2;
(2)单调递减区间：-1.5326<x<-0.7315以及0<x<1.5951.
(2)
函数的图形为：
clear
>> fplot('3*x^5-20*x^3+10',[-3,3])
ans =
-3
最值2：
x=1:0.1:3;
>> y=3.*x.^5-20.*x.^3+10;
>> [m k]=max(y)
m =
199
k =
21
>> x(k)
ans =
3
驻点1及相应的二阶导数值：
clear
>> syms x y
>> y=3*x^5-20*x^3+10;
>> yxx=diff(y,x,2);
>> grid on
f=inline('100*acos(1-1/200*(r^2))+r^2*acos(1/20*r)-10*sqrt(r^2-1/400*r^4)-50*pi','r');
>> y=fzero(f,12)
y =
11.5873
3.求解下列非线性方程组在远点附近的根：
clear
>> syms x y z
>> [x y z]=solve('9*x^2+36*y^2+4*z^2-36','x^2-2*y^2-20*z','16*x-x^3-2*y^2-16*z^2',x,y,z)

推导出了动力学方程
������������⁄������������ = ������������(1 − (������ + ������)) − ������1������∗������,
（4 − 3）
������������∗⁄������������ = −������1������∗������ + ������2������
二、 问题分析
建立肿瘤细胞增长模型时，我们可以从自由增长模型开始分析，引进 Logistic 阻滞增长模型，构成肿瘤细胞增长初步框架。再者肿瘤细胞不同于普 通细胞，其生长受到人体自身免疫系统的制约。于是综合考虑正常细胞转化，癌 细胞增殖，癌细胞死亡，癌细胞被效应细胞消除等情况，建立动力学方程。并对 模型进行适当简化求解。在放射治疗方案的设计中，我们可以引入放射生物学中 广泛接受的 LQ 模型对问题进行分析，由于放疗对人体伤害相当大，因此我们采 取分次逐次放疗的方式进行治疗。我们具体分两种情形进行讨论，一是在总剂量 一定的条件下，不同的分次剂量组合对生物效应的影响；二是在产生相同生物效 应的情况下，分析最优的分次剂量组合。
易算出癌细胞转入活动期已有 300 多天，故如何在早期发现癌症是攻克癌症的关键之一 （2）手术治疗常不能割去所有癌细胞，故有时需进行放射疗法。射线强度太小无法杀
死癌细胞，太强病人身体又吃不消且会使病人免疫功能下降。一次照射不可能杀死全部癌细 胞，请设计一个可行的治疗方案（医生认为当体内癌细胞数小于 100000 个时即可凭借体内 免疫系统杀灭）。
进一步简化，根据(4-4)，(4-5)式可知，效应细胞������∗和复合物������有出有进．假 设出入保持平衡，则有
������ + ������∗ = C (C 为常数)

1.1.2 MATLAB命令形式 命令形式
在工作空间或MATLAB命令窗口中输入 命令窗口中输入MATLAB 在工作空间或 命令窗口中输入 认可的任何命令，按回车键都可执行其操作. 认可的任何命令，按回车键都可执行其操作 如“4+7”、“4-7”、“4*7”、“4/7”、 “4^5”， 、 、 、 、 ， 等按回车键后可显示其结果. “sqrt(5)”等按回车键后可显示其结果 等按回车键后可显示其结果
随机抽取10 名学生的高等数学课程成绩， 例1.2.2 随机抽取 名学生的高等数学课程成绩， 并统计他们中的最高分、 并统计他们中的最高分、最低分以及他们的平均 成绩。 成绩。
math=[88,90,77,69,92,80,74,66,95,85]; %产生 维向量 产生10维向量 产生 mathaver=sum(math)/10 %计算平均成绩 计算平均成绩 h=max(math) l=min(math) %求出最高分 求出最高分 %求出最低分 求出最低分
第一章 MATLAB使用说明 1.1 MATLAB窗口环境与命令形式
1.1.1 Matlab 的窗口环境
当前工 作目录 当前工 作空间 命令 提示符 命令窗口 输入命令的 历史记录
运行MATLAB创建一个或多个窗口
a) 命令区 命令区(Command Window)是用户使用的主 是用户使用的主 要场所，此时，可以输入变量、 要场所，此时，可以输入变量、数组及运算命 进行一些简单的运算； 键搜索、 令，进行一些简单的运算；用↑↓←→键搜索、 键搜索 修改以前使用过的命令操作, 清除窗口; 修改以前使用过的命令操作 用 clc清除窗口 清除窗口 寻求有关帮助; 用help sqrt ( help input …)寻求有关帮助 寻求有关帮助 b) 编辑区 编辑区(Editor\Debugger Window)编制各种 编制各种 M-文件，存盘 文件， 文件 存盘(Save)、运行（Run）等. 、运行（ ）

1.9.1 求极限
表 1.9.1 limit 函数的用法
表达式
函数格式
备注
lim x→a f (x) lim x→a− f (x) lim x→a+ f (x) lim x→a f (x)
limit(f, x, a) limit(f, x, a, ’left’) limit(f, x, a, ’right’) limit(f, a)
format long
15 位数字表示
3.14159265358979
format short e 5 位科学记数表示
3.1416e+00
format long e 15 位科学记数表示
3.14159265358979e+00
format short g 从 format short 和 format short e 中自动选最佳记述方式 3.1416
ans =
-1/12
（2） lim x→2
x−2 x2x-2)/(x^2-4),x,2)
ans =
1/4
（3） lim x→+∞
(1 +
t )4x 2x
>> syms x t
>> limit((1+t/(2*x))^(4*x),x,inf)
-1-
《数学实验》
第一讲 MATLAB 软件基本操作
1.1 MATLAB 软件简介
MATLAB 的名称源自 Matrix Laboratory,是一门计算语言，它专门以矩阵的 形式处理数据。MATLAB 将计算与可视化集成到一个灵活的计算机环境中，并提供 了大量的内置函数。可以在广泛的工程问题中直接利用这些函数获得数值解。

x=-10:0.6:10; y=x; [X,Y]=meshgrid(x,y); Z=sin(pi.*sqrt(X.^2+Y.^2)); surf(X,Y,Z) xlabel('x') ylabel('y') zlabel('z') title('z=sin(pi*sqrt(x.^2+y.^2)') shading flat
其各位数字的立方和等于该数本身。例如，153是一个水仙花数，因为153=1 计算程序
for a=1:1:9 for b=0:1:9 for c=0:1:9 A=a*100+b*10+c; if A==a^3+b^3+c^3 disp(A)
end end end end 最终结果： 153 370 371 407 分析：此题使我进一步熟悉了循环语句for、while等的基本格式和应用方法， 得注意的是每一个循环语句或条件语句的出现，必定要对应的出现一个end，这 点很容易忽视。 6．编写函数M-文件sq.m：用迭代法求的值。求平方根的迭代公式为 程序： function f=sq(a) a>=0 x=eps; y=1/2*(x+a/x); while (abs(x-y)>=10^(-5)) x=y y=1/2*(x+a/x) end f=x else disp('their exist errors') end 运行结果 调用sq(16)，输出结果是4.0000 分析：此题要求掌握利用循环语句进行迭代，实现开方方程的求解，另外x的取
分析在表达乘方的时候要用“y1=x.^2”的形式，在表达x分量的时候可以用 linspace和直接用 生成数组的形式。主要函数：plot：生成图片；hold on和old off用来在同一幅图 描图；text：用程序对图片加标注；gtext：用鼠标在图中加字符；title：用于对 加标题。

实验一 常微分方程1. 分别用Euler 法和ode45解下列常微分方程并与解析解比较： (1) ,(0)1,13y x y y x '=+=<<Euler 法：function [t,y]=euler(Fun,tspan,y0,h) t=tspan(1):h:tspan(2); y(1)=y0;for i=1:length(t)-1y(i+1)=y(i)+h.*feval(Fun,t(i),y(i)); end t=t'; y=y';function f=Fun(x,y) % 常微分方程的右端函数 f=x+y;>> [x,y]=euler('Fun',[0,3],1,0.1)>> [x,y] ans =0 1.0000 0.1000 1.1000 0.2000 1.2200 0.3000 1.3620 0.4000 1.5282 0.5000 1.7210 0.6000 1.9431 0.7000 2.1974 0.8000 2.4872 0.9000 2.8159 1.0000 3.1875 1.1000 3.6062 1.2000 4.0769 1.3000 4.6045 1.4000 5.1950 1.5000 5.8545 1.6000 6.5899 1.7000 7.4089 1.8000 8.3198 1.9000 9.3318 2.0000 10.4550 2.1000 11.7005 2.2000 13.0805 2.3000 14.6086 2.4000 16.2995 2.5000 18.1694 2.6000 20.2364 2.7000 22.5200 2.8000 25.0420 2.9000 27.8262 3.0000 30.8988ode45：>> [x,y]=ode45('Fun',[0,3],1) ans =0 1.0000 0.0502 1.0528 0.1005 1.1109 0.1507 1.17460.2010 1.2442 0.2760 1.3596 0.3510 1.4899 0.4260 1.63610.5010 1.7996 0.5760 1.9817 0.6510 2.1838 0.7260 2.4074实验一 常微分方程0.8010 2.6544 0.8760 2.9264 0.9510 3.2254 1.0260 3.55351.1010 3.9131 1.1760 4.3065 1.2510 4.7364 1.3260 5.20561.4010 5.7172 1.4760 6.2744 1.5510 6.8810 1.6260 7.54061.7010 8.2574 1.7760 9.0359 1.8510 9.8808 1.9260 10.79742.0010 11.7912 2.0760 12.8683 2.1510 14.0351 2.2260 15.29862.3010 16.6664 2.3760 18.1466 2.4510 19.7478 2.5260 21.47962.6010 23.3522 2.6760 25.3764 2.7510 27.5641 2.8260 29.92812.9010 32.4820 2.9257 33.3694 2.9505 34.2796 2.9752 35.21343.0000 36.1711解析解：>> y=dsolve('Dy=x+y','y(0)=1','x') y =2*exp(x) - x - 1(2) 20.01()2sin(),(0)0,(0)1,05y y y t y y t ''''-+===<< Euler 法：实验一常微分方程function f=Fun(t,y)% 常微分方程的右端函数f=[y(2);0.01*y(2)^2-2*y(1)+sin(t)];>> [t,y]=euler('Fun',[0,5],[0,1],0.2)ode45：>> [t,y]=ode45('Fun',[0,5],[0,1])t =0 0.0001 0.0001 0.0002 0.0002 0.0005 0.0007 0.0010 0.0012 0.00250.0037 0.0050 0.0062 0.0125 0.0188 0.0251 0.0313 0.0627 0.0941 0.12550.1569 0.2819 0.4069 0.5319 0.6569 0.7819 0.9069 1.0319 1.1569 1.28191.4069 1.5319 1.6569 1.7819 1.90692.0319 2.1569 2.2819 2.4069 2.53192.6569 2.7819 2.90693.0319 3.1569 3.2819 3.4069 3.5319 3.6569 3.78193.90694.0319 4.1569 4.2819 4.4069 4.5319 4.6569 4.7427 4.8285 4.91425.0000y =0 1.0000 0.0001 1.0000 0.0001 1.0000 0.0002 1.0000 0.0002 1.00000.0005 1.0000 0.0007 1.0000 0.0010 1.0000 0.0012 1.0000 0.0025 1.00000.0037 1.0000 0.0050 1.0000 0.0062 1.0000 0.0125 1.0000 0.0188 1.00000.0251 0.9999 0.0313 0.9998 0.0627 0.9987 0.0941 0.9965 0.1253 0.99340.1564 0.9893 0.2786 0.9632 0.3966 0.9220 0.5085 0.8662 0.6126 0.79670.7072 0.7146 0.7908 0.6210 0.8620 0.5176 0.9198 0.4058 0.9632 0.28760.9915 0.1647 1.0043 0.0392 1.0013 -0.0869 0.9826 -0.2117 0.9485 -0.33310.8996 -0.4490 0.8365 -0.5578 0.7605 -0.6577 0.6725 -0.7471 0.5742 -0.8246实验一 常微分方程0.4669 -0.8889 0.3525 -0.9393 0.2327 -0.9748 0.1095 -0.9950 -0.0154 -0.9996-0.1398 -0.9887 -0.2619 -0.9624 -0.3798 -0.9212 -0.4916 -0.8657 -0.5957 -0.7970-0.6904 -0.7161 -0.7742 -0.6242 -0.8460 -0.5228 -0.9046 -0.4134 -0.9491 -0.2978-0.9789 -0.1777 -0.9934 -0.0549 -0.9945 0.0300 -0.9883 0.1146 -0.9748 0.1985-0.9543 0.28092. 求一通过原点的曲线，它在(,)x y 处的切线斜率等于22,0 1.57.x y x +<<若x 上限增为1.58，1.60会发生什么？function f=Fun(x,y) % 常微分方程的右端函数 f=2*x+y.^2;>> [x,y]=ode45('Fun',[0,1.57],0) x =0 0.0393 0.0785 0.1178 0.1570 0.1963 0.2355 0.2748 0.3140 0.3533 0.3925 0.4318 0.4710 0.5103 0.5495 0.5888 0.6280 0.6673 0.7065 0.7458 0.7850 0.8243 0.8635 0.9028 0.9420 0.9813 1.0205 1.0598 1.0990 1.1383 1.1775 1.2168 1.2560 1.2953 1.3345 1.3738 1.4130 1.4248 1.4367 1.4485 1.4604 1.4722 1.4840 1.4959 1.5077 1.5140 1.5203 1.5265 1.5328 1.5376 1.5424 1.5472 1.5519 1.5543 1.5567 1.5591 1.5614 1.5631 1.5647 1.5664 1.5681 1.5685 1.5690 1.5695 1.5700 y =实验一 常微分方程0 0.0015 0.0062 0.0139 0.0247 0.0386 0.0556 0.0758 0.09920.1259 0.1559 0.1895 0.2266 0.2675 0.3124 0.3615 0.4152 0.4738 0.5378 0.6076 0.6841 0.7679 0.8601 0.9620 1.0751 1.2014 1.3434 1.5045 1.6892 1.9037 2.1557 2.4577 2.8282 3.3003 3.9056 4.7317 5.9549 6.4431 7.0116 7.6832 8.4902 9.4821 10.7170 12.3090 14.4551 15.9220 17.7080 19.9390 22.8164 25.6450 29.2282 33.9673 40.5910 44.9434 50.3088 57.1229 66.1087 74.3108 84.7123 98.4901 117.7875 124.9206 132.9699 142.1268 152.641500.20.40.60.81 1.2 1.4 1.6若x 上限增为1.58，1.60,则超出运算的范围，发生溢出。

6、抓图，若液位太低或者溢出，可以修改QV116开度，重复4和6步。
7、将系统输出设定值置为0，关闭系统，分析数据
4实验结果与思考
系统稳定时的截图：
控制量从30%上升到35%，液位从50%上升到80%。
按照60%变动，则从52%高度画线。从开始变化到70%变动范围时间
Tc就是171秒。增益K=(70-50)/(35-30)=4
13、固定I于某一中间值，然后改变P的大小，观察加扰动后被调量输出的动态波形，据此列表记录不同值Ti下的超调量σp。
14、选择合适的P和Ti值，使系统对阶跃输入扰动的输出响应为一条较满意的过渡过程曲线。此曲线可通过改变设定值（如设定值由50%变为60%）来
获得。
15、在PI调节器控制实验的基础上，再引入适量的微分作用，即把软件界面上设置D参数，然后加上与前面调节时幅值完全相等的扰动，记录系统被控制量响应的动态曲线。
b)
1.实验目的与要求
了解PID控制特点，掌握PID的调节规律；通过实验，掌握PID参数的整定。
1、实验前需熟悉实验的设备装置以及管路构成。
2、熟悉仪表装置，如检测单元、控制单元、执行单元等。
3、分别用P,PI,PD,PID整定出最佳的比例度、积分时间和微分时间。
2实验设备及工艺流程
1、实验设备：A1000对象系统
（1）水泵U102(P102)
（2）水泵调速器：工作电源24VAC，控制信号2-10VDC
（3）液位传感器：量程为0-100%,输出信号4-20mA。
2、系统组成
单容水箱液位PID控制流程图如图3.2.1所示，采用右边支路进行实验，左边支路也是一样的。测点清单如表3.2.1所示。
3操作步骤和调试
每个实验的实验步骤都列出在实验界面的左边，可供参考。下面仅给出单容液位控制的操作步骤。注意：A1000垂直双容需要打开中间阀门，需要高液位一端的液位不能低于阀门。

第一次练习题1． 求032=-x e x 的所有根。

（先画图后求解）>> fplot('[exp(x)-3*x^2,0]',[-5,5]);>> grid on>> fsolve('exp(x)-3*x^2',-1) Equation solved.fsolve completed because the vector of function values is near zero as measured by the default value of the function tolerance, and the problem appears regular as measured by the gradient. <stopping criteria details> ans =-0.4590Optimization terminated: first-order optimality is less than options.TolFun.ans =-0.4590fsolve('exp(x)-3*x^2',1)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =0.9100>> fsolve('exp(x)-3*x^2',4)Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.<stopping criteria details>ans =3.7331求得此方程的三个根2． 求下列方程的根。

一个有趣的数学小实验摘要 如今不少南京市民家烧开水既可以用电也可以用天然气，那么到底选择哪种更经济划算呢？近日，我就做了一次“用天然气烧水省钱还是用电烧水省钱”的有趣数学小实验。

结果发现，平底壶烧水在“峰时”用天然气比用电划算；在“谷时”用电比用天然气划算；天然气烧水时用中火比用大火更省钱。

关键词 平底壶 天然气 峰时 谷时一、实验的起因当，当，当，听见有人敲门我问一了句“谁呀，有什么事？”“收费！”门外的声音回答到，妈妈一听，马上跑了出去，回来时拿着收费单子和爸爸抱怨说“这个月怎么又是这么多钱啊！”我一听到妈妈的话就明白了，我们家每个月的开支中水费、电费、天然气费就要花不少钱，全是因为没有做到节约，浪费现象比较严重。

比如家里一直用天然气烧水，而那个水壶的报警器早就坏了，现在水烧开了不自动报警了，经常是水开了没人知道，等想起来去看水时，水只剩一半了，又得重新烧一壶，如此反复下去，浪费许多时间不说，更重要的是浪费了许多能源和钱。

想到这里我再也坐不住了，让爸爸去重新买个水壶，这样可以每月节省不少家用开支。

爸爸说现在家里烧开水既可以用电也可以用天然气，可以买电水壶也可以买普通水壶，如果我们考虑要节能省钱，那么到底选择哪种更经济划算呢？这倒把我难住了，我还从来没有考虑到这个问题，我赶紧上网去查，网上有的人认为用电划算，原因是电水壶的热损失少，热效率高于燃气，但也有认为煤气烧水会快一点，电水壶虽然也快，但是瓦数太高了，用电比较多，一个月电费合起来也会很贵。

我茫然了，想来想去，决定亲自实验一下，让爸爸去把两种水壶都买回来，我来做个对比实验，用实验数据来解答这个问题。

二、实验的工具某品牌型号一只4升平底电水壶（功率为1.5千瓦）；一只4升平底水壶；电子计时器。

三、实验过程先将水壶装满4升水，将天然气调到最大档，用大火开始烧，记录天然气表的起始刻度，用电子计时器记录烧水的起始时间。

水烧开后鸣叫，此时记录天然气表的最终刻度和终止时间。

图1-9 八次拟合Βιβλιοθήκη 第1章函数与极限—设计性实验
实验二
复利问题
【实验目的】 1.加深对函数极限概念的理解 2.讨论极限在实际问题中的应用 3.会用Matlab命令求函数极限 【实验要求】 掌握极限概念，Matlab软件求函数极限的命 令limit
第1章函数与极限—设计性实验
【实验内容】
复利，即利滚利。不仅是一个经济问题，而且是 一个古老又现代的经济社会问题。随着商品经济 的发展，复利计算将日益普遍，同时复利的期限 将日益变短，即不仅用年息、月息，而且用旬息、 日息、半日息表示利息率。现在我们已进入电子 商务时代，允许储户随时存款或取款，如果一个 储户连续不断存款和取款，结算本息的频率趋于 无穷大，每次结算后将本息全部存入银行，这意 味着银行不断地向储户支付利息，称为连续复利 问题。
第1章函数与极限--验证性实验
【实验内容】 1．求下列函数的复合函数 (1) f 1 , g sin y ，求
1 x2
f ( g ( y))
【实验过程】 1.（1）>>syms x y >> f=1/(1+x^2); >> g=sin(y); >> compose(f,g) 运行结果： ans = 1/(sin(y)^2+1) 由上述结果可知：
本金+利息= p(1+r/n)+ p(1+r/n)*r/n =p(1+r/n)2 ……，
第n期到期后的本利和是 p(1+r/n)n 存期为t年(事实上是有tn期)，到期后的本利和为 p(1+r/n)tn 随着结算次数的无限增加，即在上式中n→∞,t=1 年后本息共计 n lim100000 r/n） ≈10.6184(万元) （1+ n 随着结算次数的无限增加，一年后本息总和将稳 定于10.6184万元，储户并不能通过该方法成为百 万富翁。

第四章 实验视角下的函数研究（下）从从属关系看，三角函数属于函数范畴．但它又有其特殊性，因此开设独立章节，专题对它的运算、图象及其性质展开研究．第1节 三角函数定义及同角三角函数关系验证在初中阶段学习了锐角的三角函数定义．以锐角α为直角三角形的一个内角，则对边邻边，邻边对边，斜边邻边，斜边对边====ααααcot tan cos sin ． 根据这个定义，我们提出了这样的疑问：如果锐角α的大小没有改变，而改变了它所在的直角三角形的大小，对应的三角函数值会发生改变吗？如果会，这样的定义就是不合理的，三角函数值的计算也是不可行的．下面，验证这个疑问．【实验1】锐角三角函数定义合理性的验证 【探究步骤】1．在GGB 中点击“参数”工具，设定参数α，把参数类型设置为“角度”，范围设置为]900[，； 2．在x 轴正半轴任取一点A ，并作出坐标原点O ；3．点击“定值角度”工具，然后依次点击点O A ,，在弹出的对话框中，设定角度为α，GGB 将作出满足条件的角α终边上一点'A ；4．作出射线'OA ；5．在射线'OA 上取一点C ，过点C 作CD 垂直x 轴于D ； 6．隐藏多余元素，作出OCD Rt ∆；7．设定精确度为“保留５位小数”，测量边CD OC OD ,,的长度； 8．计算CDODOD CD OC OD OC CD ，，，的值，设置颜色为红色； 9．拉动点C ，改变OCD Rt ∆的大小．注意到，只要角α的大小没有改变，CDODOD CD OC OD OC CD ，，，都没有改变．【说明】步骤３中的“定值角度”，可以使得所作的角和滑杆对应的参数α相等，也可以根据需要作出诸如3022+ααα，，之类的角．【思考】本例为什么不直接过点'A 作x 轴的垂线，而要在射线'OA 上任选一点C 来作垂线呢？ 通过本例的探究说明：CDODOD CD OC OD OC CD ，，，这些比值只与角α的大小有关，而与OCD Rt ∆的大小无关．由此，可以认定这样定义锐角的三角函数值是合理的．【实验2】验证坐标法定义三角函数的合理性高中阶段，为了满足研究三角函数的需要，引入了任意角三角函数的定义．因为角度的任意性，已经无法在直角三角形中定义三角函数，因此，教材引入了任意角三角函数的坐标法定义．在平面直角坐标系xOy 中，以坐标原点为角α的顶点，x 轴非负半轴为角α的始边，根据角α的大小，作出它的终边．在终边上任取异于原点的任意一点),(y x P ，并设r OP =，定义：yx x y r x r y ====ααααcot tan cos sin ，，，．特别地，如果取点P 为终边与单位圆122=+y x 的交点，则yxx y x y ====ααααcot tan cos sin ，，，．对于任意角三角函数的坐标法定义，以下两点是存疑的：（1）坐标法定义的三角函数对于锐角α，其数值与【实验1】的相应数值相等吗？如果不是，则坐标法定义就失去其合理性；（2）如果在任意角α的终边上取两个不同点，其计算结果一致吗？ 给出以下探究： 【探究步骤】首先验证存疑点（1）：在【实验1】所作课件的基础上，作以下修改： 1．在锐角α终边OC 上任取一点P ，并测量距离OP ，设之为r ； 2．在指令栏内输入“r P y /)(”，得到测量值，并把它的名称改为“αsin ”； 3．点击代数栏中的αsin 计算结果不放，把它拉到算式OCCD的边上，设置颜色为蓝色，以方便比对；4．用同样的方法，求出αααcot ,tan ,cos 的值，并逐一放置到对应式子的边上；5．拉动滑杆α，改变角度α的大小，观察角α改变的过程中，两种定义所得的相应三角函数值是否总是相等．观察发现，无论锐角α为何值，这两种定义相应的三角函数值总是相等的．对于存疑点（2）的验证比较简单，拉动点P ，使之在终边上自由移动，移动过程中，注意观察角α的三角函数值是否发生改变．观察，点P 移动过程中，角α的三角函数值并未发生改变，这说明角α的三角函数值只与角α的大小有关，而与终边上所取的点P 的位置无关，从而证明了利用单位圆定义三角函数的合理性．我们从代数层面验证了应用坐标法定义任意角三角函数的合理性．下面给出任意角三角函数的几何直观表示．为了直观表示出任意角的三角函数，教材引入了三角函数线的概念，三角函数线的本质就是有向线段． 在平面直角坐标系xOy 中，以坐标原点为角α的顶点，x 轴非负半轴为角α的始边，根据角α的大小，作出它的终边．设终边与单位圆122=+y x 相交于点P ，作PM 垂直x 轴于点M ，设角α的终边（或终边的反向延长线）与过点)01(，A 的x 轴垂线相交于点T ．定义有向线段MP 为正弦线，有向线段OM 为余弦线，有向线段AT 为正切线．以上定义的三角函数线如何直观表示角α的三角函数值呢？教材采用以下方法：首先定义三角函数线的正方向与坐标轴的正方向相同，引入有向线段的数量，如果三角函数线的方向为正方向，则数量为正，反之为负，并定义数量的绝对值等于有向线段的长度．关于三角函数线还有更简单的理解．我们可以把向量MP 的纵坐标、OM 横坐标、AT 的纵坐标分别定义为角α的正弦值、余弦值和正切值．下面给出应用三角函数线定义任意角三角函数合理性的验证．【实验3】验证三角函数线定义三角函数的合理性 【探究步骤】1．按以上定义在单位圆中作出任意角α的三角函数线；2．点击“向量”工具，然后依次点击点P M 、，作出向量MP ，用同样的方法作出向量OM 、AT ； 3．设点P 的坐标为()y x ,，由单位圆中任意角的三角函数定义，计算出xyx y ===αααtan ,cos ,sin ； 4．设置精确度为小数点后5位，把以上算得的三角函数值分别和向量MP 的纵坐标、OM 横坐标、AT的纵坐标作比较；5．拉动点P ，观察以上对应数值是否逐一相等．经观察，无论点P 在什么位置，代数法定义的三角函数值和三角函数线的数量总是相等的．这证明了用三角函数线表示三角函数值的合理性和正确性．【思考】你能仿照上例作正切线的方法，作出余切线吗？【实验4】验证同角三角函数关系式教材给出了单位圆中任意角的三角函数定义后，重点研究了同角三角函数的关系式，给出了两个重要关系：1cos sin ,cos sin tan 22=+=ααααα 前者称为商数关系，后者称为平方关系． 如果在【实验2】基础上再给出以下定义：yx y x ===αααcot ,1csc ,1sec ， 并分别称它们为角α的正割、余割和余切．那么同角三角函数将会有更多关系被发现． 首先，根据定义，容易找到的是倒数关系：1cot tan ,1sec cos ,1csc sin =⋅=⋅=⋅αααααα其次，还可以得到两个商数关系：ααααααsin cos cot ,cos sin tan ==． 另外，还有三个平方关系：αααααα222222csc cot 1,sec tan 1,1cos sin =+=+=+这是因为αα2222222sec 11tan 1==+=⎪⎭⎫ ⎝⎛+=+x x y x x y 同理αα2222222csc 11cot 1==+=⎪⎪⎭⎫ ⎝⎛+=+y y y x y x 通过数学实验对以上结果进行验证：【探究步骤】1．在【实验3】课件的基础上，分别计算出角α的６个三角函数值； 2．分别计算上述等式的左边和右边；3．改变角α的大小，观察对任意的α值，左右两边是否相等．经检验，以上等式对于等式有意义的角α都是成立的，从而验证了同角三角函数关系式的正确性．【实验5】三角函数拓展研究 【探究问题1】如果α为锐角，探究αααtan ,sin ,的大小关系． 【探究步骤】1．把角度的度量单位改为弧度；2．在平面直角坐标系xOy 中，以坐标原点为角α的顶点，x 轴非负半轴为角α的始边，作出锐角α的终边．设终边与单位圆122=+y x 在第一象限的圆弧交于点P ，角α的终边（或终边的反向延长线）与过点)01(，A 的x 轴垂线相交于点T ，作正弦线MP ，余弦线OM ，正切线AT ；3．测量出)20(tan ,sin ,παααα<<的大小；4．拉动点P ，观察αααtan ,sin ,的大小关系． 观察发现，只要20πα<<，总有αααtan sin <<．【思考】 只要20πα<<，总有αααtan sin <<，这是为什么呢？能给出证明或者几何方面的直观解释吗？事实上，只要20πα<<，总有OAT OAP OAP S S S ∆∆<<扇形（详见本题配套课件中的图形）．即αααtan 2121sin 21<<，从而得到αααtan sin <<． 【探究问题２】拉动点P ，使得点P 与点A 无限靠近，观察αα与sin 的值，你会发现什么？ 经过观察，可以发现，若0→α，则αα≈sin ．为了说明这个问题，在【探究问题1】的基础上，给出以下探究． 【探究步骤】在【探究问题1】课件的基础上，作以下修改：1．设定参数⎪⎭⎫⎝⎛∈2,0πα； 2．点击“定值角度”工具，然后依次点击点O A ,，在弹出的对话框内输入角度α； 3．作出角α终边与圆弧的交点P ； 4．测量P 的纵坐标，则)(sin P y =α；5．把精确度调整到小数点后15位，计算ααsin -的值；6．点击“按钮”工具，在弹出的对话框中设置按钮名称为“0→α”，并在脚本框中输入代码“2/αα=”．每点击一次按钮，角度α将变成原来的21，这样经过若干次的点击，角度α很快就趋近于０了，在点击的过程中，注意观察ααsin -的值的变化．可以注意到，当0→α时，0sin →-αα．即当0→α时，αα≈sin ．【探究问题３】 若21sin =α，求角α． 这是最简单的三角方程，初中阶段只研究锐角三角函数时，显然答案只有一个，6πα=．但高中阶段把角度的范围扩大到了任意角，那么，在R ∈α的条件下，方程21sin =α的解又是什么呢？ 【探究步骤】1．打开本节【实验３】课件；2．拉动点P 从点A 起，沿逆时针方向旋转，旋转过程中，注意观察αsin 的数值变化．我们观察到，当角α的终边在第一、第二象限时，0sin >α，当角α的终边在第三、第四象限时，0sin <α，要使21sin =α成立的角α只能是一、二象限角． 再次重复刚才的实验，进一步观察，又可以发现：当⎥⎦⎤⎢⎣⎡∈2,0πα时，αsin =y 单调递增，其函数值从０增大到1，当⎥⎦⎤⎢⎣⎡∈ππα,2时，αsin =y 单调递减，其函数值从１减少到０.以上实验结果表明：当[]πα,0∈，有且只有两个α值满足21sin =α． 第三次重复以上实验，发现在[]πα,0∈，能使得21sin =α成立的α是65,6ππ，考虑到当角α终边转过整数圈回到65,6ππ终边位置时，仍满足21sin =α，满足条件的角α应表示为：)(652,62Z ∈+=+=k k k ππαππα或，即)(6)1(Z ∈-+=k k k ππα．【拓展探究1】 若21cos =α，求角α． 【拓展探究2】 若1tan =α，求角α．结合【实验３】课件，作自主探究． 【探究问题4】 若21sin >α，求角α的取值范围． 本题可在【探究问题3】的基础上继续深入，由【探究问题3】可知：当⎥⎦⎤⎢⎣⎡∈2,0πα时，αsin =y 单调递增，其函数值从０增大１，当⎥⎦⎤⎢⎣⎡∈ππα,2时，αsin =y 单调递减，其函数值从１减少到０.以上实验结果表明：当[]πα,0∈，满足21sin >α的角α的范围是656παπ<<．考虑到角α终边转过整数圈回到⎪⎭⎫ ⎝⎛65,6ππ时，不等式仍然成立．因此满足21sin >α的角α取值范围是)(652,62Z ∈⎪⎭⎫⎝⎛++k k k ππππ． 【拓展探究３】 若21sin <α，求角α的取值范围． 【拓展探究4】 若21cos <α，求角α的取值范围． 【拓展探究5】若1tan >α，求角α的取值范围．以上拓展探究问题，请读者结合【实验３】课件作自主探究．。

“离散数学”实验报告(实验1)专业班级学号姓名目录一.实验目的； ....................................... - 1 -二.实验内容； ....................................... - 2 -1. 逻辑联接词的运算 ..................................................................................................... - 2 -2. 求任意一个命题公式的真值表 ................................................................................. - 2 -三.实验环境； ....................................... - 2 -四. 实验原理和实现进程（算法描述）；................. - 2 -1.实验原理 ....................................................................................................................... - 2 -2.实验进程 ....................................................................................................................... - 3 -五.实验数据及结果分析；.............................. - 7 -题A：................................................................................................................................ - 7 - B,C题：............................................................................................................................ - 9 - 六. 源程序清单； ................................... - 13 -A题部份源代码： .......................................................................................................... - 13 - tt:printf("***************************************\n");其他收成和体会。