数学建模斜拉桥设计
- 格式:doc
- 大小:2.76 MB
- 文档页数:16

midas斜拉桥建模⽬录概要 1桥梁基本数据 2荷载 2设定建模环境 3定义材料和截⾯特性值 4成桥阶段分析 6建⽴模型 7建⽴加劲梁模型 8建⽴主塔 9建⽴拉索 11建⽴主塔⽀座 12输⼊边界条件 13索初拉⼒计算 14定义荷载⼯况 18输⼊荷载 19运⾏结构分析 24建⽴荷载组合 24计算未知荷载系数 25查看成桥阶段分析结果 29查看变形形状 29正装施⼯阶段分析 30正装施⼯阶段分析 34正装施⼯阶段分析 34正装分析模型 36定义施⼯阶段 38定义结构组 41定义边界组 48定义荷载组 53定义施⼯阶段 59施⼯阶段分析控制数据 64运⾏结构分析 65查看施⼯阶段分析结果 66查看变形形状 66查看弯矩 67查看轴⼒ 68查看计算未闭合配合⼒时使⽤的节点位移和内⼒值 69成桥阶段分析和正装分析结果⽐较 70概要斜拉桥是塔、拉索和加劲梁三种基本结构组成的缆索承重结构体系,桥形美观,且根据所选的索塔形式以及拉索的布置能够形成多种多样的结构形式,容易与周边环境融合,是符合环境设计理念的桥梁形式之⼀。
为了决定安装拉索时的控制张拉⼒,⾸先要决定在成桥阶段恒载作⽤下的初始平衡状态,然后再按施⼯顺序进⾏施⼯阶段分析。
⼀般进⾏斜拉桥分析时⾸先通过倒拆分析计算初张拉⼒,然后进⾏正装施⼯阶段分析。
在本例题将介绍建⽴斜拉桥模型的⽅法、计算拉索初拉⼒的⽅法、施⼯阶段分析⽅法、采⽤未闭合配合⼒功能只利⽤成桥阶段分析张⼒进⾏正装分析的⽅法。
本例题中的桥梁模型为三跨连续斜拉桥(如图1),主跨110m、边跨跨经为40m。
图 1. 斜拉桥分析模型桥梁基本数据为了说明斜拉桥分析步骤,本例题采⽤了较简单的分析模型,可能与实际桥梁设计内容有所差异。
本例题桥梁的基本数据如下。
桥梁形式三跨连续斜拉桥桥梁跨经 40.0 m + 110.0 m + 40.0 m = 190.0 m 桥梁⾼度主塔下部 : 20m ,主塔上部 : 40m图 2. ⽴⾯图荷载分类荷载类型荷载值⾃重⾃重程序内部⾃动计算索初拉⼒初拉⼒荷载满⾜成桥阶段初始平衡状态的索初拉⼒挂篮荷载节点荷载 80 tonf ⽀座强制位移强制位移10 cm使⽤MIDAS/Civil 软件内含的优化法则计算出索初拉⼒。


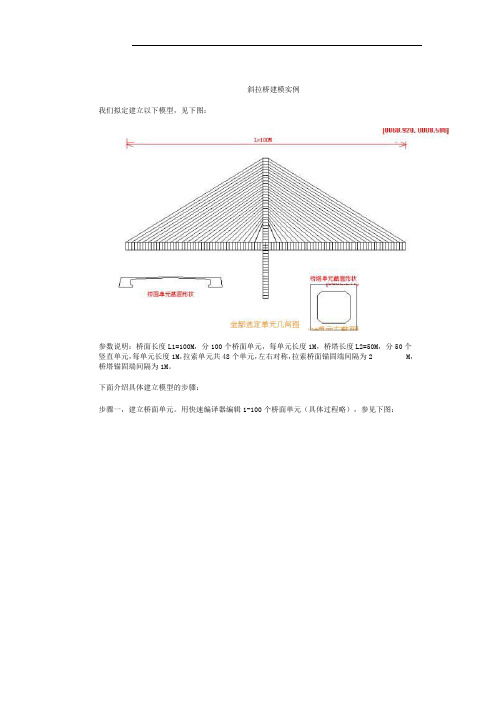
斜拉桥建模实例我们拟定建立以下模型,见下图:参数说明:桥面长度L1=100M,分100个桥面单元,每单元长度1M,桥塔长度L2=50M,分50个竖直单元,每单元长度1M,拉索单元共48个单元,左右对称,拉索桥面锚固端间隔为2 M,桥塔锚固端间隔为1M。
下面介绍具体建立模型的步骤:步骤一,建立桥面单元。
用快速编译器编辑1-100个桥面单元(具体过程略),参见下图:(注:在实际操作中桥面的截面形状可以自己拟定)步骤二:建立桥塔单元。
用快速编译器编辑101-150个桥塔单元(具体过程略),参见下图:(注:在实际操作中桥面的截面形状可以自己拟定,在分段方向的单选框内,一定要选择“竖直”,起点x=49,y=-20,终点x=49,y=30是定义桥塔的位置,这里我把它设在桥面中部,桥面下20米处,因为我做的桥塔截面为2m×2m的空心矩形,所以此处起点和终点x填49,请读者自己理解)步骤三:拉索的建立。
A、先编辑桥塔左边部分24跟拉索单元。
点击快速编译器的“拉索”按钮,在拉索对话框内的编辑内容复选框选择编辑节点号勾上,编辑单元号:151-174,左节点号:1-48/2;右节点号:152-129;(注意:左节点1-48/2代表拉索在桥面的锚固点间距为2M),如下图:在快速编译器中选择“单元”按钮,在“单元”对话框内的复选框内把“截取坐标”勾上,编辑单元号:151-174,然后确定。
如下图:B、建立桥面右半部分的24跟拉索。
在快速编译器中选择“对称”按钮,在“对称”对话框中的编辑内容4个复选框都勾上。
模板单元组:151-174;生成单元组:198-175;左节点号:55-101/2;右节点号:129-152;对称轴x=50,然后确定。
见下图:这样,我们就建好了拉索单元的模型。
现在让我们来看一看整个模型的三维效果图:。


目录概要斜拉桥是塔、拉索和加劲梁三种基本结构组成的缆索承重结构体系,桥形美观,且根据所选的索塔形式以及拉索的布置能够形成多种多样的结构形式,容易与周边环境融合,是符合环境设计理念的桥梁形式之一。
为了决定安装拉索时的控制张拉力,首先要决定在成桥阶段恒载作用下的初始平衡状态,然后再按施工顺序进行施工阶段分析。
一般进行斜拉桥分析时首先通过倒拆分析计算初张拉力,然后进行正装施工阶段分析。
在本例题将介绍建立斜拉桥模型的方法、计算拉索初拉力的方法、施工阶段分析方法、采用未闭合配合力功能只利用成桥阶段分析张力进行正装分析的方法。
本例题中的桥梁模型为三跨连续斜拉桥(如图1),主跨110m、边跨跨经为40m。
图 1. 斜拉桥分析模型桥梁基本数据为了说明斜拉桥分析步骤,本例题采用了较简单的分析模型,可能与实际桥梁设计内容有所差异。
本例题桥梁的基本数据如下。
桥梁形式 三跨连续斜拉桥桥梁跨经 40.0 m + 110.0 m + 40.0 m = 190.0 m 桥梁高度 主塔下部 : 20m ,主塔上部 : 40m图 2. 立面图荷载分 类荷载类型 荷载值自重 自重 程序内部自动计算索初拉力 初拉力荷载 满足成桥阶段初始平衡状态的索初拉力挂篮荷载 节点荷载 80 tonf 支座强制位移强制位移10 cm设定建模环境为了做斜拉桥成桥阶段分析首先打开新项目“cable stayed ”为名保存文件,开始建立模型。
单位体系设置为“m ”和“tonf ”。
该单位体系可以根据输入的数据类型随时随意更换。
文件 /新项目文件 / 保存(cable stayed) 工具 / 单位体系长度 > m ;力 > tonf ↵图 3. 设定建模环境及单位体系定义材料和截面特性值输入加劲梁、主塔下部、主塔上部、拉索的材料特性值。
在材料和截面对话框中选择材料表单点击按钮。
模型 / 材料和截面特性 /材料名称(加劲梁) 设计类型 > 用户定义弹性模量(2.1e7) ; 泊松比(0.3)容重(7.85)↵按上述方法参照表1输入主塔下部、主塔上部、拉索的材料特性值。
BIM技术在斜拉桥有限元分析中的应用一、概述随着科技的不断发展,建筑信息模型(BIM)技术在工程领域的应用越来越广泛。
斜拉桥作为一种重要的交通工程结构形式,其设计和施工过程中对有限元分析的需求也日益增加。
BIM技术作为一种集成化的建筑设计和管理工具,可以有效地辅助斜拉桥的有限元分析,提高分析的准确性和效率。
本文将探讨BIM技术在斜拉桥有限元分析中的应用,包括BIM技术的基本原理、在斜拉桥设计阶段的应用以及在施工阶段的应用,并通过实际案例分析验证了BIM技术在斜拉桥有限元分析中的优势和价值。
1. 斜拉桥的概述斜拉桥是一种跨越河流、峡谷等地形障碍的桥梁结构,其主要特点是在主梁上设置一个或多个斜向索塔,通过索塔与主梁之间的钢索连接,形成一个整体结构。
斜拉桥的设计和施工技术对于保证桥梁的安全性能和使用寿命具有重要意义。
随着科技的发展,建筑信息模型(BIM)技术在斜拉桥有限元分析中的应用越来越广泛,为斜拉桥的设计、施工和维护提供了有力支持。
BIM技术是一种基于三维可视化的建筑设计和管理工具,通过对建筑物的各个构件进行数字化建模,实现设计、施工、运营和维护等全过程的信息化管理。
在斜拉桥有限元分析中,BIM技术可以为设计师提供更加直观、准确的桥梁结构模型,有助于提高设计的精度和效率。
同时BIM技术还可以实现多专业协同设计,促进各专业之间的信息共享和沟通,降低设计风险。
有限元分析是一种计算流体力学方法,通过对结构模型施加边界条件和加载条件,模拟结构的受力过程,从而评估结构的强度、刚度和稳定性等性能。
在斜拉桥有限元分析中,有限元方法可以帮助设计师识别潜在的结构问题,优化设计方案,提高桥梁的安全性能。
此外有限元分析还可以为斜拉桥的施工提供技术支持,如预制构件的设计、施工过程的模拟等。
BIM技术在斜拉桥有限元分析中的应用为桥梁设计和施工提供了新的思路和技术手段,有助于提高斜拉桥的质量和安全性,降低工程成本,推动桥梁行业的可持续发展。
斜拉桥设计
摘要:
模型是建立在对斜拉桥造价预算基础上的一类数学建模问题。
模型的建立的初衷是对斜拉桥的设计提出合理美观的设计方案,且同时要尽量节省资金。
在对模型的建立与求解的过程之前先是对斜拉桥总体外观进行了设计,确定了水上的桥面长度与引桥的长度,以及引桥的支撑方式。
模型的建立与求解是建立在模型假设的条件基础上,模型假设的提出为解决实际问题提供了方便。
例如,索塔顶部的拉索部分并不是从同一节点引出,但假设同一节点之后更加方便简洁的有助于我们对斜拉桥的拉索的造价进行估算。
在模型中由于索塔个数不同对索塔造价和拉索造价的影响确定了多种方案,从各方案的造价进行比较,确定最佳方案。
关键词:外观假设节点最佳方案
一、问题重述
如果计划在抚河某处修建一座斜拉桥,斜拉桥示意图和建桥处河道的截面图已分别划出。
给出几项简化假设:
(1)在桥面处,索塔造价是同样长度的水上桥面的2倍;
(2)100米长斜拉索与10米长水上前面造价相当;
(3)索塔造价与离桥面的距离平方成正比;斜拉索造价与其长度成正比;
(4)如果有陆地上的引桥的桥面,造价是水上桥面的一半;
1,请给出斜拉桥设计图,使其合理美观;
2,估算斜拉桥的造价,尽量节省资金。
图1 斜拉桥
河流截面图(单位m)
二、模型假设
1.假设斜拉桥的桥面是水平
2.假设斜拉桥的拉索的最大张角是45°
3.假设斜拉桥水面上每米的造价是5万元
4.假设模型中计算的拉索的个数索塔个数为整数
5.假设抚州地区的基岩深度为七米桩基深度为30米
6.在抚河剖面上补考虑地形起伏影响基岩距地表都为7米
7.斜拉索在索塔上的节点都为塔顶位置
8.假设主跨与次跨的长度相同
三、符号说明
1.i索塔个数
2.X
∇索塔单边拉索的最大水平距离
3.α每个索塔的单边拉索个数
l第α个索拉索长度
4.
α
5.t(1) 拉索的总长度
6.s表示各部分的造价
7.p表示各部分的价格
8.H索塔的长度的总和
9.W斜拉索桥的总造价
四、模型的建立与求解
4.1斜拉桥侧面设计图如下:
对于索塔个数n 的不同可将拉索桥的图进行适当的改变,下图为索塔n=2时的斜拉桥侧面图
4,2斜拉桥造价预算数学计算计算基础
拉索的每米的造价:
万元5.05100
10
)1(=⨯=
p 索塔每米的造价:
万元10)4(2)5(=⨯=p p
陆地上引桥部分每米桥面的造价:
万元.52)4(5.0)2(==p p
引桥部分桥墩每米造价:
万元10)5()3(==p p
索塔个数i :
x
2800
i ∇=
每个索塔的单边拉索个数:
2*d x
(拉索的相邻间距)
∇
=
α
三角形的余弦公式:
︒-+=45cos 2)b (a 2
2cb c )(
第α个索拉索长度:
︒-+=45cos d 22)2(l 22αααh d h )(
拉索的总长度:
αα
l *411
∑==i i t )(
拉索的总造价:
)1()1()1(P t s ⨯=
引桥总造价:
)2()(s(2)p l ⨯=引桥长度
引桥支柱长度:
25)()(+=桩基深度引桥支柱长度a h
引桥支柱造价:
)3()()3(p h s ⨯=引桥柱长度
河上的桥面造价:
)4(8004p s ⨯=)(
当300120≤∇-≤X n )(时, 如图竖直线位置:
75
'
300)12(h X n =∇-
索塔底部到防洪水位线的直线距离:
12
X
)12(3'∇-=
n h
索塔长度:
25X ')(+++∇=a h i h
当500)12(300≤∇-≤X n 时 如图竖直线位置:
索塔底部到防洪水位线的直线距离:
h
75
'=
索塔长度:
+∇
+
h
i
h
=a
(+
X
25
)
'
当500
≤X
-
n时
2(
∇
)1
300≤
如图竖直线位置:
75
"
300500)12(h X n =-∇-
"h 的值为
[]12
500)12(3"-∇-=
X n h
索塔底部到防洪水位线的直线距离:
"75'h h -=
索塔长度:
25X ')(+++∇=a h i h
则索塔长度函数表达式为:
25X ')(+++∇=a h i h
所有索塔的长度的总和:
∑==、
n 1i )(H i h
索塔的总造价:
)5()5(P H s ⨯= 斜拉索桥的总造价:
∑==
5
1
)(i i s w
4.3斜拉桥的造价预算结果
对4.2中的公式用visualbasic 编程计算得到如下结果,计算的程序及程序界面见附录:
由表知当索塔n=5时斜拉桥的造价最低,为17960.3万元。
五、模型的优点与缺点
模型的优点:
本模型采用了计算机上的循环算法的思想,分别对索塔的个数i进行进行从一开始赋值计算出多种方案下的预算进行比较,采用这种方法可以根据计算出的预算结果进行直观的比较从而寻找到最佳的预算方案。
模型的缺点:
本模型刚开始时所计算出的方案并不一定符合实际情况,但是对最后的最佳的但是对最后的最佳方案的选择结果并没有影响。
六、模型的改进
本模型仅对防洪警戒水位以下的桥面部分建成了斜拉式桥,而将新桥部分没有用拉索固定。
采用的是用混凝土底座支撑引桥部分。
对对于这个问题可将引桥部分也改用斜拉索式进行固定,看是否更加美观,同时还能降低建桥的成本。
七、参考文献
1、visualbasic程序设计【蒋琪尚宏白延丽】
2、部分斜拉桥设计与实践【何新平】
3、斜拉桥设计说明【百度文库】
4、卫星和飞船的监测【张兆桥薛鹏飞宫浩亮】
附录一:
Dim n As Integer
Private Sub Form_Click()
Print "索塔个数"; n
s3 = 55
s2 = 500
s4 = 4000
a = 30
d = 5
Dim x As Single
Dim c As Integer
Dim hl, hm As Single
x = 800 / (2 * n) '单边拉索的水平长度
c = Int(x / d) '每个索塔的单边拉索个数p1 = 0.5
Dim i As Integer
Dim lsum As Single
Dim li As Single
For i = 1 To c
li = Sqr(((Sqr(2)) * x) ^ 2 + (i * d) ^ 2 - 2 * (Sqr(2)) * x * i * d * Cos(3.14 / 4))
lsum = lsum + li
Next i
s1 = 4 * lsum * p1 '拉索的总造价
p5 = 10
Dim j As Integer
Dim hsum As Single
Dim hj As Single
Dim w As Single
For j = 1 To n
If (2 * n - 1) * x <= 300 Then
hl = ((2 * n - 1) * x * 3) / 12
hj = hl + 25 + a + x
ElseIf 300 < (2 * n - 1) * x <= 500 Then
hl = 75
hj = hl + 25 + a + x
Else
hm = ((2 * n - 1) * x - 500) * 3 / 12
hl = 75 - hm
hj = hl + 25 + a + x
End If
hsum = hsum + hj
Next j
s5 = hsum * p5
Print "拉索的总造价"; s1; "万元"
Print "引桥处路面的总造价"; s2; "万元"
Print "引桥处桥墩的总造价"; s3; "万元"
Print "防洪警戒线以下的桥面造价"; s4; "万元" Print "索塔造价"; s5; "万元"
w = s1 + s2 + s3 + s4 + s5 '斜拉索桥的总造价Print "拉索桥总造价"; w; "万元"
End Sub
Private Sub Form_Load()
n = Val(InputBox("索塔个数")) '索塔个数
End Sub
附录二、。