悬链线计算坐标

悬链线常数
悬链线（Catenary）指的是一种曲线，是两端固定的一条（粗细与质量分布）均匀、柔软（不能伸长）的链条，在重力的作用下所具有的曲线形状。

悬链线的数学方程是一个双曲余弦函数，其标准形式为y = a cosh(x/a)，其中a是悬链线顶点到横坐标轴的距离，也是方程式中的常数，即悬链线常数。

悬链线常数是描述悬链线特性的一个重要参数，与悬链线的形状和物理特性有关。

例如，在悬索桥等结构设计中，悬链线常数会影响桥梁的承重能力和稳定性等方面。

如需更具体的信息，建议咨询数学或物理专业人士，或查阅相关书籍文献作为参考。

悬链线坐标计算程序悬链线是一种理想化的模型，用于描述物体自身重力和张力平衡的关系。

在物理学和工程学中，悬链线常常被用于计算和分析各种结构的力学性质。

本文将介绍悬链线的坐标计算程序，以及它在实际问题中的应用。

我们来了解一下什么是悬链线。

悬链线是指在重力作用下，一个柔性、均匀且无质量的绳子所呈现的形状。

在悬链线的模型中，绳子的张力在各个点上都是相等的，同时满足重力和张力的平衡条件。

悬链线的形状是一个平滑曲线，通常被描述为一个无法解析求解的函数，因此需要使用数值计算方法来确定其坐标。

为了计算悬链线的坐标，我们可以使用迭代方法。

首先，我们假设绳子的初始形状为一条直线段。

然后，通过迭代计算，逐步调整绳子的形状，直到达到所期望的精度要求为止。

在每一步迭代中，我们根据当前绳子的形状，计算绳子上各个点的张力和重力分量，并根据平衡条件调整绳子的形状。

在实际计算中，我们可以将悬链线分成若干个小段，每个小段内的形状近似为一条直线。

然后，我们可以根据每个小段的起始点和长度，计算出小段的末端坐标，并将其作为下一个小段的起始点。

通过重复这个过程，我们可以逐步计算出悬链线上各个点的坐标。

悬链线的坐标计算程序可以使用各种编程语言来实现，例如Python、C++等。

在程序中，我们需要定义悬链线的长度、重力加速度等参数，并设置迭代的精度要求。

然后，我们可以使用循环结构来逐步计算悬链线的坐标，直到达到所要求的精度为止。

最后，我们可以将计算得到的悬链线坐标输出到文件或打印在屏幕上，以供进一步分析和应用。

悬链线的坐标计算程序在工程学和物理学中有着广泛的应用。

例如，在桥梁和吊塔的设计中，我们需要计算悬链线的形状和张力分布，以确定结构的稳定性和安全性。

此外，悬链线的模型还被用于分析电缆、输送带等柔性结构的力学性质，以及模拟绳索、链条等物体的运动和变形。

悬链线的坐标计算程序是一种重要的工具，用于分析和计算各种结构的力学性质。

通过迭代方法，我们可以逐步计算出悬链线上各个点的坐标，并通过这些坐标来分析和应用悬链线模型。

悬链线方程的推导过程悬链线是一种曲线，其形状类似于悬链。

悬链线最早由德国数学家焦若贝利在1725年所提出，也被称为Catenary（猫enary）曲线。

这条曲线具有许多独特的性质和应用领域，因此悬链线的推导过程也非常有趣。

悬链线的推导涉及到一些微积分和几何的知识。

在这里，我将尽量简明扼要地介绍悬链线方程的推导过程。

第一步：设定问题和坐标系我们假设有一根不可伸长、重力平均作用于其上的悬链线。

我们希望找到这条悬链线的方程。

为此，我们首先将悬链线放在一个笛卡尔坐标系中。

设悬链线的轴线为x轴，y轴垂直于轴线。

第二步：表示悬链线的参数方程为了表示悬链线，我们引入参数t，表示悬链线上任意一点的位置。

我们假设悬链线的最低点为原点O(0, 0)，则悬链线的参数方程可以表示为：x = at， y = bch(a)，其中a和b是任意的正数，c是一个常数，表示悬链线的形状。

第三步：应用欧拉－积分方程为了求解悬链线的参数方程，我们需要应用欧拉－积分方程。

欧拉－积分方程是描述弹性形体的自平衡状态的一个重要方程。

我们令L表示悬链线的弧长，则有：L = ∫√(1 + (dy/dx)²)dx将悬链线的参数方程带入上式，可以得到：L = ∫√(1 + (a² + b²ch²(a)²)dt第四步：求解悬链线弧长的积分通过对上式中的积分进行变量替换和一些微积分的技巧可以求得L的积分形式。

最终我们得到：L = ∫csch(a)da，其中csch(a)是双曲正弦函数的倒数，定义为csch(a) = 1/sinh(a) = (2e^a)/(e^2a - 1)第五步：应用数值积分方法由于上述积分无法通过标准的解析方法求解，我们可以应用数值积分方法来计算L。

一种常用的数值积分方法是龙格－库塔法则，它可以在较高精度下计算复杂的积分。

第六步：求解悬链线方程通过数值积分得到L后，我们可以尝试通过方程L=c来求解a。

悬链线科技名词定义中文名称：悬链线英文名称：catenary定义：两端悬挂的理想柔性软索的曲线。

工程计算中，可近似用抛物线计算。

应用学科：电力（一级学科）；输电线路（二级学科）以上内容由全国科学技术名词审定委员会审定公布目录悬链线等高悬链线数学表达式的证明工程中的应用悬链线悬链线(Catenary) 是一种曲线，它的形状因与悬在两端的绳子因均匀引力作用下掉下来之形相似而名。

适当选择坐标系后，悬链线的方程是一个双曲余弦函数，其公式为：y = a*cosh(x/a) 其中a 是一个常数。

等高悬链线数学表达式的证明注释如右图，设最低点A处受水平向左的拉力H，右悬挂点处表示为C点，在AC弧线区段任意取一段设为B点，则B受一个斜向上的拉力T，设T 和水平方向夹角为θ，绳子的质量为m,受力分析有：Tsinθ=mg；Tcosθ=H，tanθ=dy/dx=mg/H，mg=ρs，，其中s是右段AB 绳子的长度，ρ是绳子线重量密度，代入得微分方程dy/dx=ρs/H;利用弧长公式ds=√(1+dy^2/dx^2)*dx;所以s=∫√(1+dy^2/dx^2)*dx; 所以把s 带入微分方程得dy/dx=ρ∫√(1+dy^2/dx^2)*dx/H;.....(1) 对于(1)设p=dy/dx微分处理得p'=ρ/H*√(1+p^2)......(2) p'=dp/dx; 对（2）分离常量求积分∫dp/√(1+p^2)=∫ρ/H*dx 得ln[p+√(1+p^2)]=ρx/H+C，即asinhp（反双曲正弦）=ρx/H+C 当x=0时，dy/dx=p=0；带入得C=0；整理得asinhp=ρx/H 另祥解：（ln[p+√(1+p^2)]=ρx/H）；p=sh(ρx/H) （1+p^2=e^(2ρx/H)-2pe^(ρx/H)+p^2）；(p=[e^(ρx/H)-e^(-ρx/H)]/2=dy/dx)；y=ch (ρx/H)* H / ρ（y=H/(2ρ)*[e^(ρx/H)+e^(-ρx/H)] ）；令a=H/ρ：y=a*cosh (x/a) (y=a[e^(x/a)+e^(-x/a)]/(2)= a*cosh(x/a))。

悬链线坐标计算程序悬链线是一种特殊的曲线，其形状类似于一条悬挂的链条。

在工程学和物理学中，悬链线的数学模型被广泛应用于桥梁、电线、杆塔等结构的设计和分析。

为了计算悬链线的坐标，可以编写一个简单的计算程序。

我们需要了解悬链线的一些基本概念。

悬链线是一条自由悬挂的曲线，在重力的作用下，曲线的形状会发生变化。

悬链线上的每个点都受到重力的作用，因此曲线的形状是由重力平衡条件决定的。

为了计算悬链线的坐标，我们可以采用数值计算的方法。

具体步骤如下：1. 假设悬链线的起始点坐标为(x0, y0)，重力加速度为g。

选择合适的步长h。

2. 从起始点开始，依次计算曲线上的每个点的坐标。

假设当前点的坐标为(xi, yi)。

3. 根据重力平衡条件，计算当前点的斜率。

斜率的计算公式为：k = -g * (xi - x0) / (yi - y0)4. 根据斜率和步长h，计算下一个点的坐标。

下一个点的坐标可以通过以下公式计算：xi+1 = xi + hyi+1 = yi + k * h5. 重复步骤4，直到达到所需的终点。

通过编写一个悬链线坐标计算程序，我们可以方便地计算悬链线上任意点的坐标。

程序的基本框架如下：```pythondef catenary_coordinates(x0, y0, g, h, end):# 初始化起始点坐标xi = x0yi = y0# 计算悬链线上的每个点的坐标while xi <= end:# 计算斜率k = -g * (xi - x0) / (yi - y0)# 计算下一个点的坐标xi += hyi += k * h# 输出当前点的坐标print("悬链线上点({:.2f}, {:.2f})".format(xi, yi))# 主程序入口if __name__ == "__main__":# 设置悬链线的起始点坐标、重力加速度、步长和终点坐标x0 = 0.0y0 = 0.0g = 9.8h = 0.1end = 10.0# 调用悬链线坐标计算函数catenary_coordinates(x0, y0, g, h, end)```通过运行上述程序，我们可以得到悬链线上任意点的坐标。

悬链线科技名词定义中文名称：悬链线英文名称：catenary定义：两端悬挂的理想柔性软索的曲线。

工程计算中，可近似用抛物线计算。

应用学科：电力（一级学科）；输电线路（二级学科）以上内容由全国科学技术名词审定委员会审定公布目录悬链线等高悬链线数学表达式的证明工程中的应用悬链线悬链线(Catenary) 是一种曲线，它的形状因与悬在两端的绳子因均匀引力作用下掉下来之形相似而名。

适当选择坐标系后，悬链线的方程是一个双曲余弦函数，其公式为：y = a*cosh(x/a) 其中a 是一个常数。

等高悬链线数学表达式的证明注释如右图，设最低点A处受水平向左的拉力H，右悬挂点处表示为C点，在AC弧线区段任意取一段设为B点，则B受一个斜向上的拉力T，设T 和水平方向夹角为θ，绳子的质量为m,受力分析有：Tsinθ=mg；Tcosθ=H，tanθ=dy/dx=mg/H，mg=ρs，，其中s是右段AB 绳子的长度，ρ是绳子线重量密度，代入得微分方程dy/dx=ρs/H;利用弧长公式ds=√(1+dy^2/dx^2)*dx;所以s=∫√(1+dy^2/dx^2)*dx; 所以把s 带入微分方程得dy/dx=ρ∫√(1+dy^2/dx^2)*dx/H;.....(1) 对于(1)设p=dy/dx微分处理得p'=ρ/H*√(1+p^2)......(2) p'=dp/dx; 对（2）分离常量求积分∫dp/√(1+p^2)=∫ρ/H*dx 得ln[p+√(1+p^2)]=ρx/H+C，即asinhp（反双曲正弦）=ρx/H+C 当x=0时，dy/dx=p=0；带入得C=0；整理得asinhp=ρx/H 另祥解：（ln[p+√(1+p^2)]=ρx/H）；p=sh(ρx/H) （1+p^2=e^(2ρx/H)-2pe^(ρx/H)+p^2）；(p=[e^(ρx/H)-e^(-ρx/H)]/2=dy/dx)；y=ch (ρx/H)* H / ρ（y=H/(2ρ)*[e^(ρx/H)+e^(-ρx/H)] ）；令a=H/ρ：y=a*cosh (x/a) (y=a[e^(x/a)+e^(-x/a)]/(2)= a*cosh(x/a))。

悬链线长度计算公式悬链线，这名字听起来是不是有点高大上？感觉很神秘，让人摸不着头脑。

其实啊，悬链线在咱们的生活中还挺常见的呢！比如说，咱们常见的那种老式的晾衣绳，当它两端固定，中间自然下垂的时候，它的形状就接近悬链线。

还有那种大型桥梁的钢索，也常常呈现出悬链线的形态。

那悬链线的长度要怎么计算呢？这就得提到悬链线长度的计算公式啦。

悬链线的长度计算公式为：$L = s + \frac{a}{2}( \sinh\frac{2s}{a} - \sinh\frac{2s_1}{a} )$ ，其中 $L$ 表示悬链线的长度，$s$ 表示两个端点的水平距离，$a$ 是一个与悬链线的物理性质有关的常数，$s_1$ 表示起始点到计算点的水平距离。

这个公式看起来是不是有点复杂？别担心，咱们一点点来理解。

先来说说这个 $s$ ，它就是两端点的水平距离，比如说晾衣绳两端固定点之间的水平距离。

$a$ 这个常数呢，它跟绳子的材料、粗细等有关系。

假设咱们有一根晾衣绳，两端固定在相距 5 米的两个点上，这 5 米就是 $s$ 。

然后通过对绳子材料的测量和分析，咱们知道了 $a$ 的值是2 。

接下来，咱们要计算从一端开始 2 米处到另一端的这段悬链线的长度。

那这里的 $s_1$ 就是 2 米。

把这些值代入公式里：$L = 5 + \frac{2}{2}( \sinh\frac{2×5}{2} -\sinh\frac{2×2}{2} )$ 。

这时候就得算一下这个 sinh 函数的值啦。

sinh 函数是双曲正弦函数，它的计算可能有点复杂，不过现在咱们有计算器或者数学软件，很容易就能得出结果。

经过计算，就能得出这段悬链线的长度。

再举个例子，假如有一座大桥，钢索的两端相距 100 米，通过对钢索的测量和分析，$a$ 的值是 10 。

咱们要计算从一端开始 30 米处到另一端的这段钢索的长度，也就是悬链线的长度。

同样把相应的值代入公式：$L = 100 +\frac{10}{2}( \sinh\frac{2×100}{10} - \sinh\frac{2×30}{10} )$ 。

通常任何材料包括导线在内,都具有一定得刚性,但由于悬挂在杆塔上得一档导线相对较长,因此导线材料得刚性对其几何形状得影响很小,故在计算中假定:ﻫ(１)导线为理想得柔索。

因此,导线只承受轴向张力(或拉力),任意一点得弯矩为ﻫ零。

这样导线力学计算可应用理论力学中得柔索理论进行计算。

ﻫ(2)作用在导线上得荷载均指同一方向,且沿导线均匀分布。

一、悬链线方程及曲线弧长1。

悬链线方程为了分析方便,我们先从悬挂点等高,即相邻杆塔导线悬挂点无高差得情况讨论导线得应力及几何关系。

实际上,导线悬在空中得曲线形态,从数学角度用什么方程来描述就是进行导线力学分析得前题、由于假定视导线为柔索,则可按照理论力学中得悬链线关系来进行分析,即将导线架设在空中得几何形态视为悬链形态,而由此导出得方程式为悬链线方程。

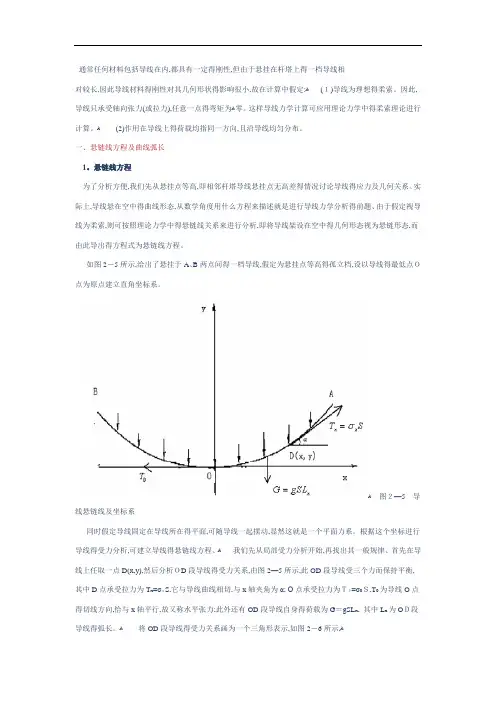
如图2－5所示,给出了悬挂于A、B两点间得一档导线,假定为悬挂点等高得孤立档,设以导线得最低点Ｏ点为原点建立直角坐标系。

ﻫ图２—5导线悬链线及坐标系同时假定导线固定在导线所在得平面,可随导线一起摆动,显然这就是一个平面力系。

根据这个坐标进行导线得受力分析,可建立导线得悬链线方程、ﻫ我们先从局部受力分析开始,再找出其一般规律、首先在导线上任取一点D(x,y),然后分析ＯD段导线得受力关系,由图2—5所示,此OD段导线受三个力而保持平衡,其中D点承受拉力为T x=σｘS,它与导线曲线相切,与x轴夹角为α; O点承受拉力为Ｔ０=σ0Ｓ,T0为导线O点得切线方向,恰与x轴平行,故又称水平张力;此外还有OD段导线自身得荷载为G＝gSL x, 其中L x为OＤ段导线得弧长。

ﻫ将OD段导线得受力关系画为一个三角形表示,如图2－6所示,ﻫﻫ图2-６导线受力情况ﻫ由静力学平衡条件可知,在平面坐标系中,其水平分力,垂直分力得代数与分别等于零。

或沿x 轴或y轴上分力代数与分别等于零。

垂直方向分力G＝T x siｎα=gSLｘ;水平方向分为Ｔ0=T xｃosα=σ0Ｓ、其中σ0、T0为导线最低点得应力与张力,σx、T x为导线任一点得应力与张力,S、g为导线截面与比载。

悬链线坐标计算程序悬链线，也称为链线，是一种常见的曲线形状，常用于工程和建筑中的设计和计算。

悬链线具有平衡力学性质，在各个点上受力相等，可以用于设计桥梁、拱门等结构。

本文将介绍一个悬链线坐标计算程序，该程序能够根据给定的参数计算悬链线的坐标。

程序将使用Python语言编写。

程序的主要逻辑如下：1.用户从程序中输入所需的参数，包括悬链线的长度（L）和起伏程度（k）。

2. 程序根据输入的参数计算悬链线的坐标。

悬链线的数学表示为y = k*cosh(x/k)，其中cosh为双曲余弦函数。

3.程序将计算出的坐标输出给用户，并绘制悬链线的图形。

下面是程序的详细实现：```python#导入所需的库import numpy as npimport matplotlib.pyplot as plt#获取用户输入的参数L = float(input("请输入悬链线的长度："))k = float(input("请输入悬链线的起伏程度："))#计算悬链线的坐标x = np.linspace(-L/2, L/2, 1000) # 生成- L/2 到 L/2 的间隔为1000 的均匀分布的数组y = k * np.cosh(x/k) # 计算悬链线的纵坐标#输出坐标print("悬链线的坐标为：")for i in range(len(x)):print("x = {:.2f}, y = {:.2f}".format(x[i], y[i]))#绘制悬链线的图形plt.plot(x, y)plt.xlabel("x")plt.ylabel("y")plt.title("悬链线")plt.grid(True)plt.show```程序的运行结果将首先输出计算出的所有坐标，然后显示悬链线的图形。