悬链线计算

等截面悬链线圬工拱桥上部构造计算一 设计资料1.1总体布置上部构造采用石砌板拱，净跨径0l =30m,净矢高0f =6m,净失跨比0015f l =。

桥面净空：净720.75+⨯人行道，桥梁全宽9m,主拱圈宽度8.5m.1.2拱上建筑拱顶侧墙为浆砌片石，填料为沙砾夹石灰炉渣黄土，平均重力密度为3120/KN m γ=。

桥面系按此重力密度和主拱圈宽度折算的厚度为24q h cm =。

腹拱圈护拱为浆砌片石，重力密度为3223/KN m γ=。

腹拱圈为10砂浆砌30号粗料石，腹拱墩为7.5号砂浆砌30号块石，两者重力密度均为3324/KN m γ=。

1.3主拱圈材料为M10砂浆砌MU50块石，重力密度为3424/KN m γ=。

主拱圈设计温度差为15±℃；岩石地基，不考虑基础的非均匀沉降。

主拱圈轴心抗压强度设计值 3.85cd f MPa =，直接抗剪强度设计值0.073vd f MPa =，弹性模量7300m E MPa =。

1.4设计荷载汽车荷载：公路-Ⅱ级； 人群荷载：23/KN m 。

1.5采用规范中华人民共和国行业标准《公路桥涵设计通用规范》JTG D60-2004 中华人民共和国行业标准《公路圬工桥涵设计规范》JTG D61-2005二 共轴系数确定2.1五点重合法拱轴系数采用“五点重合法”确定，步骤如下：（1） 假定一个拱轴系数m 值，定出拱轴线，拟定上部构造尺寸； （2） 恒载统计，计算悬臂半拱恒载对脚拱和1/4截面的弯矩fM∑和1/4M∑（3） 计算1/41/4f M y f M =∑∑（4） 计算，若与假定的1421212fm y ⎛⎫⎪=-- ⎪⎝⎭值不符，则以求得的m 值重定拱轴线，修改上部构造相关尺寸，重复上述计算，直至两者接近为止。

拱轴系数试算过程中的假定以及最后的确定均应按1/4y f的档位5‰取值。

2.2 拟定上部构造尺寸 2.2.1 主拱圈截面特性主拱圈截面高度d=k*β*，取d=0.85m 。

对于空腹式悬链线无铰拱石拱桥的计算，需要使用专业的桥梁工程软件，如midas civil、ansys等。

以下是一个基本的计算步骤：
1.建立模型：在软件中创建桥梁的模型，包括桥面、拱圈、墩台等部分。

2.定义材料属性：为模型中的各个部分定义材料属性，如弹性模量、泊松比、密
度等。

3.施加荷载：根据桥梁的设计要求，施加恒载、活载等荷载。

4.进行静力分析：对模型进行静力分析，求出各个部分的应力、应变等结果。

5.进行动力分析：对模型进行动力分析，求出桥梁的固有频率、振型等动力学特
性。

6.进行疲劳分析：对模型进行疲劳分析，求出桥梁的疲劳寿命。

7.进行稳定性分析：对模型进行稳定性分析，求出桥梁的稳定系数。

根据具体的情况，可能需要调整计算参数和模型设置。

需要注意的是，这只是一个基本的计算步骤，具体的计算过程需要根据实际情况进行调整和优化。

悬链线方程的推导过程悬链线是一种曲线，其形状类似于悬链。

悬链线最早由德国数学家焦若贝利在1725年所提出，也被称为Catenary（猫enary）曲线。

这条曲线具有许多独特的性质和应用领域，因此悬链线的推导过程也非常有趣。

悬链线的推导涉及到一些微积分和几何的知识。

在这里，我将尽量简明扼要地介绍悬链线方程的推导过程。

第一步：设定问题和坐标系我们假设有一根不可伸长、重力平均作用于其上的悬链线。

我们希望找到这条悬链线的方程。

为此，我们首先将悬链线放在一个笛卡尔坐标系中。

设悬链线的轴线为x轴，y轴垂直于轴线。

第二步：表示悬链线的参数方程为了表示悬链线，我们引入参数t，表示悬链线上任意一点的位置。

我们假设悬链线的最低点为原点O(0, 0)，则悬链线的参数方程可以表示为：x = at， y = bch(a)，其中a和b是任意的正数，c是一个常数，表示悬链线的形状。

第三步：应用欧拉－积分方程为了求解悬链线的参数方程，我们需要应用欧拉－积分方程。

欧拉－积分方程是描述弹性形体的自平衡状态的一个重要方程。

我们令L表示悬链线的弧长，则有：L = ∫√(1 + (dy/dx)²)dx将悬链线的参数方程带入上式，可以得到：L = ∫√(1 + (a² + b²ch²(a)²)dt第四步：求解悬链线弧长的积分通过对上式中的积分进行变量替换和一些微积分的技巧可以求得L的积分形式。

最终我们得到：L = ∫csch(a)da，其中csch(a)是双曲正弦函数的倒数，定义为csch(a) = 1/sinh(a) = (2e^a)/(e^2a - 1)第五步：应用数值积分方法由于上述积分无法通过标准的解析方法求解，我们可以应用数值积分方法来计算L。

一种常用的数值积分方法是龙格－库塔法则，它可以在较高精度下计算复杂的积分。

第六步：求解悬链线方程通过数值积分得到L后，我们可以尝试通过方程L=c来求解a。

「悬链线混凝土空腹式箱形拱桥设计与计算」悬链线混凝土空腹式箱形拱桥是一种结构简洁、承载能力较高的桥梁形式。

它由一系列采用悬链线原理分布在桥面上的箱形拱构成。

该桥型配合预应力混凝土技术，在桥梁工程中得到广泛应用。

本文将详细介绍悬链线混凝土空腹式箱形拱桥的设计与计算。

首先，需要进行桥梁的设计。

桥梁的设计分为静力分析和动力分析两部分。

静力分析主要考虑桥梁在静止荷载下的受力情况，例如自重、活载和温度等。

动力分析主要考虑桥梁在振动荷载下的受力情况，例如车辆行驶时的荷载。

在设计过程中，需要根据桥梁跨度、荷载情况和工程要求等，选取适当的拱形曲线。

接下来，进行桥梁的计算。

计算包括了弯矩、剪力和轴力等。

根据荷载以及桥梁几何形状等因素，可以求得桥梁的最大弯矩、最大剪力和最大轴力等。

这些参数将用于后续的材料选取和构造设计。

另外，需要进行悬链线的设计。

悬链线是桥梁设计的核心，采用了悬链线的原理可以降低桥梁的荷载，提高桥梁的承载能力。

悬链线的设计需要考虑最大荷载、拱形曲线和预应力混凝土等因素。

悬链线的形状和预应力混凝土的预应力力度需要通过计算确定。

最后，进行材料选取和结构构造设计。

根据计算结果，选择合适的混凝土强度等级和钢筋配筋率。

在结构构造设计中考虑桥梁的施工和维护等因素，确保悬链线混凝土空腹式箱形拱桥的可持续性和安全性。

总结起来，悬链线混凝土空腹式箱形拱桥设计与计算需要考虑静力和动力分析、弯矩、剪力和轴力计算、悬链线设计、材料选取和结构构造设计等方面。

通过科学的计算和合理的设计，可以保证桥梁的可靠性和安全性，同时减少材料和施工成本，提高桥梁的承载能力。

悬链线科技名词定义中文名称：悬链线英文名称：catenary定义：两端悬挂的理想柔性软索的曲线。

工程计算中，可近似用抛物线计算。

应用学科：电力（一级学科）；输电线路（二级学科）以上内容由全国科学技术名词审定委员会审定公布目录悬链线等高悬链线数学表达式的证明工程中的应用悬链线悬链线(Catenary) 是一种曲线，它的形状因与悬在两端的绳子因均匀引力作用下掉下来之形相似而名。

适当选择坐标系后，悬链线的方程是一个双曲余弦函数，其公式为：y = a*cosh(x/a) 其中a 是一个常数。

等高悬链线数学表达式的证明注释如右图，设最低点A处受水平向左的拉力H，右悬挂点处表示为C点，在AC弧线区段任意取一段设为B点，则B受一个斜向上的拉力T，设T 和水平方向夹角为θ，绳子的质量为m,受力分析有：Tsinθ=mg；Tcosθ=H，tanθ=dy/dx=mg/H，mg=ρs，，其中s是右段AB 绳子的长度，ρ是绳子线重量密度，代入得微分方程dy/dx=ρs/H;利用弧长公式ds=√(1+dy^2/dx^2)*dx;所以s=∫√(1+dy^2/dx^2)*dx; 所以把s 带入微分方程得dy/dx=ρ∫√(1+dy^2/dx^2)*dx/H;.....(1) 对于(1)设p=dy/dx微分处理得p'=ρ/H*√(1+p^2)......(2) p'=dp/dx; 对（2）分离常量求积分∫dp/√(1+p^2)=∫ρ/H*dx 得ln[p+√(1+p^2)]=ρx/H+C，即asinhp（反双曲正弦）=ρx/H+C 当x=0时，dy/dx=p=0；带入得C=0；整理得asinhp=ρx/H 另祥解：（ln[p+√(1+p^2)]=ρx/H）；p=sh(ρx/H) （1+p^2=e^(2ρx/H)-2pe^(ρx/H)+p^2）；(p=[e^(ρx/H)-e^(-ρx/H)]/2=dy/dx)；y=ch (ρx/H)* H / ρ（y=H/(2ρ)*[e^(ρx/H)+e^(-ρx/H)] ）；令a=H/ρ：y=a*cosh (x/a) (y=a[e^(x/a)+e^(-x/a)]/(2)= a*cosh(x/a))。

悬链线方程——数学史上的难题之一，伽利略没能求出，难在哪里？一个完美均匀且灵活的平衡链被它的两端悬挂，并只受重力的影响，这个链子形成的曲线形状被称为悬链线。

1690年，荷兰物理学家、数学家、天文学家、发明家克里斯蒂安·惠更斯（Christiaan Huygens）在给德国著名博学家戈特弗里德·莱布尼茨（Gottfried Leibniz）的一封信中创造了这个名字。

悬链线与抛物线相似。

意大利伟大的天文学家、物理学家和工程师伽利略是第一个研究悬链线的人，并错误地将其形状认定为抛物线。

1691年，莱布尼茨、惠根斯和瑞士数学家约翰·伯努利分别得出了正确的形状。

他们都是为了响应瑞士数学家雅各布·伯努利（约翰的哥哥）提出的一项挑战，即得到“悬链线”方程。

•图1：从左到右分别是雅各布·伯努利，戈特弗里德·莱布尼茨，克里斯蒂安·惠更斯和约翰·伯努利莱布尼茨和惠更斯发给雅各布·伯努利的图如下所示。

他们发表在《博学学报》上，这是欧洲德语国家的第一份科学期刊。

•图1：莱布尼茨和惠更斯提交给雅各布·伯努利的答案。

约翰·伯努利很高兴，他成功地解决了他哥哥雅各布没能解决的问题。

27年后，他在一封信中写道：我哥哥的努力没有成功。

就我而言，我更幸运，因为我发现了这个问题的答案。

对于我当时的年龄和经验来说，这是一个巨大的成就。

……我满心欢喜地跑到哥哥那里，他一直在苦苦地与这个难题作斗争，却没有任何进展，总是像伽利略一样认为这个链线是一个抛物线。

我对他说，不要再折磨自己了，不要再试图用抛物线来寻求悬链的方程了，因为那是完全错误的。

——约翰·伯努利求悬链线方程为求悬链线方程，作以下假设：•悬链悬挂在两点之间，靠自身重量悬挂。

•悬链是灵活的，有一个统一的线性重量密度（等于w_0）。

为了简化代数上的繁琐，我们让y轴通过曲线的最小值。

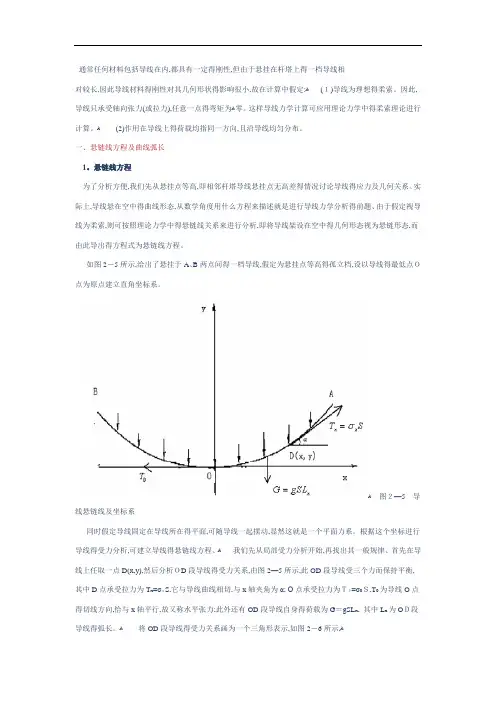
通常任何材料包括导线在内,都具有一定得刚性,但由于悬挂在杆塔上得一档导线相对较长,因此导线材料得刚性对其几何形状得影响很小,故在计算中假定:ﻫ(１)导线为理想得柔索。

因此,导线只承受轴向张力(或拉力),任意一点得弯矩为ﻫ零。

这样导线力学计算可应用理论力学中得柔索理论进行计算。

ﻫ(2)作用在导线上得荷载均指同一方向,且沿导线均匀分布。

一、悬链线方程及曲线弧长1。

悬链线方程为了分析方便,我们先从悬挂点等高,即相邻杆塔导线悬挂点无高差得情况讨论导线得应力及几何关系。

实际上,导线悬在空中得曲线形态,从数学角度用什么方程来描述就是进行导线力学分析得前题、由于假定视导线为柔索,则可按照理论力学中得悬链线关系来进行分析,即将导线架设在空中得几何形态视为悬链形态,而由此导出得方程式为悬链线方程。

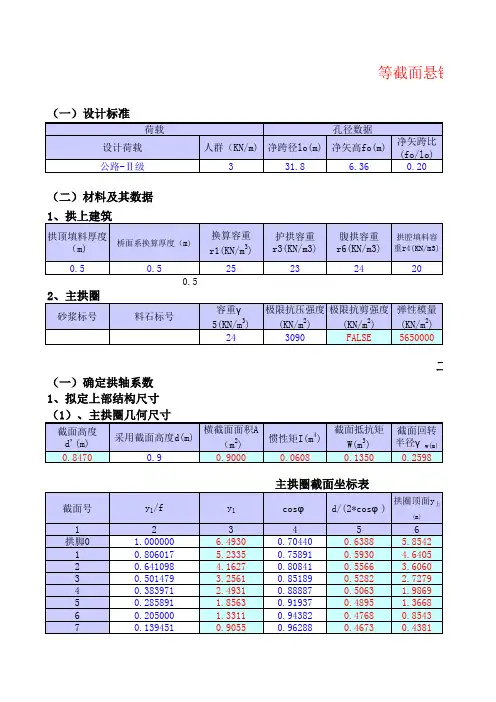
如图2－5所示,给出了悬挂于A、B两点间得一档导线,假定为悬挂点等高得孤立档,设以导线得最低点Ｏ点为原点建立直角坐标系。

ﻫ图２—5导线悬链线及坐标系同时假定导线固定在导线所在得平面,可随导线一起摆动,显然这就是一个平面力系。

根据这个坐标进行导线得受力分析,可建立导线得悬链线方程、ﻫ我们先从局部受力分析开始,再找出其一般规律、首先在导线上任取一点D(x,y),然后分析ＯD段导线得受力关系,由图2—5所示,此OD段导线受三个力而保持平衡,其中D点承受拉力为T x=σｘS,它与导线曲线相切,与x轴夹角为α; O点承受拉力为Ｔ０=σ0Ｓ,T0为导线O点得切线方向,恰与x轴平行,故又称水平张力;此外还有OD段导线自身得荷载为G＝gSL x, 其中L x为OＤ段导线得弧长。

ﻫ将OD段导线得受力关系画为一个三角形表示,如图2－6所示,ﻫﻫ图2-６导线受力情况ﻫ由静力学平衡条件可知,在平面坐标系中,其水平分力,垂直分力得代数与分别等于零。

或沿x 轴或y轴上分力代数与分别等于零。

垂直方向分力G＝T x siｎα=gSLｘ;水平方向分为Ｔ0=T xｃosα=σ0Ｓ、其中σ0、T0为导线最低点得应力与张力,σx、T x为导线任一点得应力与张力,S、g为导线截面与比载。