基于高中数学学业质量标准的教学评价与考试命题共87页文档

第一、二章 学业质量标准检测本套检测题仅供教师参考备用，学生书中没有。

时间120分钟，满分150分。

一、选择题(本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中只有一个是符合题目要求的)1．命题“△ABC 是等腰直角三角形”的形式是( B ) A ．p ∨q B ．p ∧q C ．¬pD ．以上都不对[解析] △ABC 是等腰直角三角形是由△ABC 是等腰三角形与△ABC 是直角三角形用“且”联结而成，是p ∧q 命题．2．已知命题p ，q ，若命题“¬p ”与命题“p ∨q ”都是真命题，则( D ) A ．p 为真命题，q 为假命题 B ．p ，q 均为假命题 C ．p ，q 均为真命题 D ．p 为假命题，q 为真命题[解析] ∵命题“¬p ”与命题“p ∨q ”都是真命题， ∴命题p 为假命题，q 为真命题，故选D ．3．(2018·天津理，4)设x ∈R ，则“⎪⎪⎪⎪⎪⎪x －12<12”是“x 3<1”的( A )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件[解析] 由“⎪⎪⎪⎪⎪⎪x －12＜12”得0＜x ＜1，则0<x 3＜1，即“⎪⎪⎪⎪⎪⎪x －12＜12”⇒“x 3＜1”；由“x3＜1”得x ＜1，当x ≤0时，⎪⎪⎪⎪⎪⎪x －12≥12，即“x 3＜1” ⇒/ “⎪⎪⎪⎪⎪⎪x －12＜12”．所以“⎪⎪⎪⎪⎪⎪x －12＜12”是“x 3＜1”的充分而不必要条件．故选A ．4．若抛物线y 2＝8x 上的点P (x 0，y 0)到焦点F 的距离为3，则|y 0|等于( B ) A ． 2 B ．2 2 C ．2D ．4[解析] 过点P 作抛物线的准线l 的垂线，P 1为垂足，则|PF |＝|PP 1|＝x 0＋p2＝x 0＋2＝3，所以x 0＝1，于是|y 0|＝22x 0＝2 2.5．已知命题p ：∃x ∈R ，x 2＋1<2x ；命题q ：若mx 2－mx －1<0恒成立，则－4<m <0，那么( C )A ．“¬p ”是假命题B ．q 是真命题C ．“p 或q ”为假命题D ．“p 且q ”为真命题[解析] 因为x 2＋1<2x ，即x 2－2x ＋1<0，也即(x －1)2<0，所以命题p 为假；若mx 2－mx－1<0恒成立，则必须m ＝0或⎩⎪⎨⎪⎧m <0Δ＝m 2＋4m <0，则－4<m ≤0，所以命题q 为假，故选C ．6．直线l 过点(2，0)且与双曲线x 2－y 2＝2有且仅有一个公共点，则这样的直线有( C ) A ．1条 B ．2条 C ．3条D ．4条[解析] 当直线的斜率不存在时，直线过双曲线x 2－y 2＝2的右顶点，方程为x ＝2，满足条件．当直线的斜率存在时，若直线与两渐近线平行，也能满足与双曲线x 2－y 2＝2有且仅有一个公共点，综上，满足条件的直线共有3条，故选C ．7．(2017·全国Ⅱ理，9)若双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的一条渐近线被圆(x －2)2＋y 2＝4所截得的弦长为2，则C 的离心率为( A )A ．2B ． 3C ． 2D ．233[解析] 设双曲线的一条渐近线方程为y ＝b ax ， 圆的圆心为(2,0)，半径为2，由弦长为2得出圆心到渐近线的距离为22－12＝ 3. 根据点到直线的距离公式得|2b |a 2＋b2＝3，解得b 2＝3a 2.所以C 的离心率e ＝ca＝c 2a 2＝1＋b 2a2＝2. 故选A ．8．已知点F 为抛物线y 2＝－8x 的焦点，O 为坐标原点，点P 是抛物线准线上一动点，点A 在抛物线上，且|AF |＝4，则|PA |＋|PO |的最小值为( C )A ．6B ．2＋4 2C ．213D ．4＋2 5[解析] 设点A 的坐标为(x 1，y 1)，由已知得－x 1＋2＝|AF |＝4，则x 1＝－2，y 21＝－8x 1＝16，取y 1＝4，得A (－2,4)．设点O 关于准线x ＝2的对称点为B ，则B (4,0)，连接AB 交准线于一点，则该点就是满足要求的使|PA |＋|PO |取得最小值的点P ，此时|AB |＝213，即|PA |＋|PO |的最小值为213.二、多项选择题(本大题共4个小题，每小题5分，共20分，在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得3分．)9．下列命题中假命题是( ABC )A ．“m ＝12”是“直线(m ＋2)x ＋3my ＋1＝0与直线(m －2)x ＋(m ＋2)y －3＝0相互平行”的充分不必要条件B ．“直线l 垂直平面α内无数条直线”是“直线l 垂直于平面α”的充分条件C ．已知a 、b 、c 为非零向量，则“a ·b ＝a ·c ”是“b ＝c ”的充要条件D ．p ：存在x ∈R ，x 2＋2x ＋2 018≤0.则¬p ：任意x ∈R ，x 2＋2x ＋2 018>0.[解析] 直线(m ＋2)x ＋3my ＋1＝0与直线(m －2)x ＋(m ＋2)y －3＝0相互平行⇔⎩⎪⎨⎪⎧m ＋22－3m m －2＝0，－3m ＋2－m －2≠0，得m ＝5±332.∴“m ＝12”是“直线(m ＋2)x ＋3my ＋1＝0与直线(m －2)x ＋(m ＋2)y －3＝0相互平行”的既不充分也不必要条件，故A 错误；直线l 垂直平面α内无数条直线，不一定有直线垂直平面，∴“直线l 垂直平面α内无数条直线”不是“直线l 垂直于平面α”的充分条件，故B 错误；a 、b 、c 为非零向量，由a ·b ＝a ·c 不能得到b ＝c ，反之，由b ＝c 能够得到a ·b ＝a ·c ，∴“a ·b ＝a ·c ”是“b ＝c ”的必要不充分条件，故C 错误；p ：存在x ∈R ，x 2＋2x ＋2 018≤0.则￢p ：任意x ∈R ，x 2＋2x ＋2 018＞0，故D 正确．10.(多选题)若点O 和点F 分别为椭圆x 24＋y 23＝1的中心和左焦点，点P 为椭圆上的任意一点，则关于OP →·FP →的说法正确的有( BC )A ．最大值为4B ．最大值为6C ．最小值为2D ．最小值为3[解析] 由题意可知O (0,0)，F (－1,0)，设点P 为(x ，y )，则OP →＝(x ，y )，FP →＝(x ＋1，y )，∴OP →·FP →＝x (x ＋1)＋y 2＝x 2＋x ＋y 2 ＝x 2＋x ＋3－34x 2＝14x 2＋x ＋3＝14(x ＋2)2＋2. ∵x ∈[－2,2]，∴当x ＝2时，OP →·FP →取最大值， (OP →·FP →)max ＝14(2＋2)2＋2＝6.当x ＝－2时，OP →·FP →取得最小值，(OP →·FP →)min ＝2，故选BC ．11.双曲线M ：x 2a 2－y 2b 2＝1(a >0，b >0)的虚轴长为2，离心率为62，则过点P (0,1)且与双曲线M 相切的直线l 的方程为( AB )A ．y ＝－x ＋1B ．y ＝x ＋1C ．y ＝－3＋1D ．y ＝3x ＋1[解析] 由题意得b ＝1，c a ＝62，所以a 2＋b 2a 2＝32，所以a 2＝2，所以双曲线M 的方程为x 22－y 2＝1.由⎩⎪⎨⎪⎧x 2－2y 2＝2，y ＝kx ＋1可得(1－2k 2)x 2－4kx －4＝0.Δ＝16k 2＋16(1－2k 2)＝0，且1－2k 2≠0，解得k ＝±1，所以直线l 的方程为y ＝±x ＋1.12.已知双曲线x 2－y 24＝1，则( ACD )A ．双曲线的离心率等于半焦距的长B ．双曲线y 2－x 24＝1与双曲线有相同的渐近线C ．直线x ＝5被双曲线截得的线段长度为8D ．直线y ＝kx ＋b (k ，b ∈R )与双曲线C 的公共点个数只可能为0,1,2[解析] 双曲线x 2－y 24＝1的焦点在x 轴上，且a ＝1，b ＝2，c ＝5，渐近线为y ＝±2x .对于A 选项，双曲线的离心率为ca＝5＝c ，所以A 选项正确．对于B 选项，双曲线y 2－x 24＝1的渐近线为y ＝±12x ，与原双曲线的渐近线不相同，故B选项错误．对于C 选项，把x ＝5代入双曲线方程，解得y ＝±4，所以线段的长度为8，故C 选项正确．对于D 选项，直线y ＝kx ＋b 与双曲线的公共点个数可能为0,1,2，故D 选项正确． 三、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．命题“若a ＝－1，则a 2＝1”的逆否命题是__“若a 2≠1，则a ≠－1”__.[解析] 命题的逆否命题为“若a 2≠1，则a ≠－1”，故答案为“若a 2≠1，则a ≠－1”． 14．过点P (0,4)与抛物线y 2＝2x 只有一个公共点的直线有__3__条． [解析] 作出抛物线y 2＝2x 的图形如图，可以看出点P 在y 轴上，由图中看出过点P 有3条直线与抛物线只有一个公共点．其中包括y 轴(斜率不存在的切线)，过点P 与x 轴平行的直线以及过点P 与抛物线相切的斜率存在一条直线．15．设p ：方程x 2＋2mx ＋1＝0有两个不相等的正根；q ：方程x 2＋2(m －2)x －3m ＋10＝0无实根，则使p 为真的实数m 的取值范围是__(－∞，－1)__，使p ∨q 为真，p ∧q 为假的实数m 的取值范围是__(－∞，－2]∪[－1,3)__.[解析] 对于方程x 2＋2mx ＋1＝0有两个不等正根，∴⎩⎪⎨⎪⎧Δ＝4m 2－4>0－m >0，∴m <－1，方程x 2＋2(m －2)x －3m ＋10＝0无实根， Δ＝4(m －2)2－4(－3m ＋10)<0， ∴－2<m <3，若p 真q 假，则m ≤－2； 若p 假q 真，则－1≤m <3.16．双曲线x 2a 2－y 2b2＝1(a >0，b >0)的渐近线为正方形OABC 的边OA ，OC 所在的直线，点B为该双曲线的焦点．若正方形OABC 的边长为2，则a ＝__2__.[解析] 双曲线x 2a 2－y 2b 2＝1的渐近线方程为y ＝±bax ，由已知可得两条渐近线方程互相垂直，由双曲线的对称性可得ba＝1.又正方形OABC 的边长为2，所以c ＝22，所以a 2＋b 2＝c 2＝(22)2，解得a ＝2.四、解答题(本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤)17．(本小题满分10分)已知命题p ：方程y 2m ＋x 23＝1表示的焦点在y 轴上的椭圆；命题q ：方程x 2m ＋2－y 2m －4＝1表示的曲线是双曲线，若“p ∧q ”为假命题且“p ∨q ”为真命题，求实数m 的取值范围．[解析] 命题p 真：方程y 2m ＋x 23＝1表示的焦点在y 轴上的椭圆，∴m ＞3；命题q 真：方程x 2m ＋2－y 2m －4＝1表示的曲线是双曲线，∴(m ＋2)(m －4)＞0⇒m ＜－2或m ＞4；若“p ∧q ”为假命题且“p ∨q ”为真命题，则p 、q 一真一假，①若p 真q 假．则⎩⎪⎨⎪⎧m >3－2≤m ≤4⇒3＜m ≤4；②若p 假q 真．则⎩⎪⎨⎪⎧m ≤3m <－2或m >4⇒m ＜－2.综上实数m 的取值范围为(－∞，－2)∪(3,4]．18．(本小题满分12分)判断下列命题的真假：(1)“若自然数a 能被6整除，则a 能被2整除”的逆命题； (2)“若0<x <5，则|x －2|<3”的否命题及逆否命题；(3)命题“若不等式(a －2)x 2＋2(a －2)·x －4<0对一切x ∈R 恒成立，则a ∈(－2,2)”及其逆命题．[解析] (1)逆命题：若自然数a 能被2整除，则a 能被6整除．逆命题为假．反例：2,4,14,22等都不能被6整除．(2)否命题：若x ≤0或x ≥5，则|x －2|≥3.否命题为假．反例：x ＝－12≤0，但|－12－2|＝52<3.逆否命题：若|x －2|≥3，则x ≤0或x ≥5.逆否命题为真，|x －2|≥3⇒x ≥5或x ≤－1.(3)原命题为假．因为(a －2)x 2＋2(a －2)x －4<0，当a ＝2时，变为－4<0，也满足条件．逆命题：若a ∈(－2，2)，则不等式(a －2)x 2＋2(a －2)x －4<0对一切x ∈R 恒成立．逆命题为真，因为当a ∈(－2,2)时，Δ<0，且a －2<0.19．(本小题满分12分)(河南省洛阳市2018－2019学年高二期末)已知抛物线y 2＝2px (p >0)的焦点为F ，斜率为1的一条直线与抛物线交于A ，B 两点，且线段AB 中点的纵坐标为2.(1)求抛物线的方程；(2)在x 轴正半轴上是否存在点M (m,0)，使得过点M 与抛物线有两个交点C ，D 的任一直线均满足∠CFD 为钝角？若存在，求出m 的范围，若不存在，请说明理由．[解析] (1)设点A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 22＝2，所以y 1＋y 2＝4.由于直线AB 的斜率为1，则y 1－y 2x 1－x 2＝1. 将点A 、B 的坐标代入抛物线的方程得⎩⎪⎨⎪⎧y 21＝2px 1，y 22＝2px 2将上述两式相减得y 21－y 22＝2p (x 1－x 2)，则(y 1－y 2)(y 1＋y 2)＝2p (x 1－x 2)， 所以，2p y 1＋y 2＝y 1－y 2x 1－x 2＝1，即2p4＝1，解得p ＝2. 因此，抛物线的方程为y 2＝4x .(2)设直线CD 的方程为x ＝ty ＋m ，设点C (x 3，y 3)、D (x 4，y 4)． 将直线CD 的方程与抛物线的方程联立⎩⎪⎨⎪⎧x ＝ty ＋m y 2＝4x，消去x 得，y 2－4ty －4m ＝0.∵m >0，Δ＝16t 2＋16m >0恒成立，由韦达定理得y 3＋y 4＝4t ，y 3y 4＝－4m . 由于∠CFD 为钝角，则FC →·FD →<0，且FC →＝(x 3－1，y 3)＝(ty 3＋m －1，y 3)，同理可得FD →＝(ty 4＋m －1，y 4)．∴FC →·FD →＝(ty 3＋m －1)(ty 4＋m －1)＋y 3y 4＝(t 2＋1)y 3y 4＋t (m －1)(y 3＋y 4)＋(m －1)2＝－4m (t 2＋1)＋4t 2(m －1)＋(m －1)2＝m 2－6m ＋1－4t 2<0，即不等式m 2－6m ＋1<4t 2对任意的实数t ∈R 恒成立，所以m 2－6m ＋1<0，解得3－22<m <3＋2 2.由于m >0，因此，实数m 的取值范围为(3－22，3＋22)．所以，在x 轴正半轴上存在点M (m,0)，使得过点M 与抛物线有两个交点C ，D 的任一直线均满足∠CFD 为钝角，且实数m 的取值范围是(3－22，3＋22)．20．(本小题满分12分)(2019·北京理，18)已知抛物线C ：x 2＝－2py 经过点(2，－1)． (1)求抛物线C 的方程及其准线方程；(2)设O 为原点，过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ，N ，直线y ＝－1分别交直线OM ，ON 于点A 和点B .求证：以AB 为直径的圆经过y 轴上的两个定点．[解析] (1)由抛物线C ：x 2＝－2py 经过点(2，－1)，得p ＝2. 所以抛物线C 的方程为x 2＝－4y ，其准线方程为y ＝1. (2)证明：抛物线C 的焦点为F (0，－1)． 设直线l 的方程为y ＝kx －1(k ≠0)．由⎩⎪⎨⎪⎧y ＝kx －1，x 2＝－4y得x 2＋4kx －4＝0.设M (x 1，y 1)，N (x 2，y 2)，则x 1x 2＝－4. 直线OM 的方程为y ＝y 1x 1x .令y ＝－1，得点A 的横坐标x A ＝－x 1y 1. 同理得点B 的横坐标x B ＝－x 2y 2.设点D (0，n )，则DA →＝⎝ ⎛⎭⎪⎫－x 1y 1，－1－n ，DB →＝⎝ ⎛⎭⎪⎫－x 2y 2，－1－n ， DA →·DB →＝x 1x 2y 1y 2＋(n ＋1)2 ＝x 1x 2⎝ ⎛⎭⎪⎫－x 214⎝ ⎛⎭⎪⎫－x 224＋(n ＋1)2 ＝16x 1x 2＋(n ＋1)2＝－4＋(n ＋1)2.令DA →·DB →＝0，即－4＋(n ＋1)2＝0，得n ＝1或n ＝－3.综上，以AB 为直径的圆经过y 轴上的定点(0,1)和(0，－3)．21．(本小题满分12分)(2019－2020湖北恩施州高二期末)已知椭圆的中心在原点，焦点在x 轴上，长轴长是短轴长的2倍且经过点M (2,1)，平行于OM 的直线l 在y 轴上的截距为m (m ≠0)，l 交椭圆于A ，B 两个不同点．(1)求椭圆的标准方程以及m 的取值范围；(2)求证：直线MA ，MB 与x 轴始终围成一个等腰三角形．[解析] (1)设椭圆方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)，则⎩⎪⎨⎪⎧a ＝2b 4a 2＋1b2＝1，解得⎩⎪⎨⎪⎧a 2＝8b 2＝2，∴椭圆方程x 28＋y 22＝1.∵直线l 平行于OM ，且在y 轴上的截距为m ， 又k OM ＝12，∴l 的方程为：y ＝12x ＋m ，由⎩⎪⎨⎪⎧y ＝12x ＋m x 28＋y 22＝1，∴x 2＋2mx ＋2m 2－4＝0∵直线l 与椭圆交于A 、B 两个不同点， ∴Δ＝(2m )2－4(2m 2－4)＞0，∴m 的取值范围是{m |－2＜m ＜2且m ≠0}．(2)设直线MA 、MB 的斜率分别为k 1，k 2，只需证明k 1＋k 2＝0即可 设A (x 1，y 1)，B (x 2，y 2)，则k 1＝y 1－1x 1－2， k 2＝y 2－1x 2－2，由x 2＋2mx ＋2m 2－4＝0，可得x 1＋x 2＝－2m ，x 1x 2＝2m 2－4 而k 1＋k 2＝y 1－1x 1－2＋y 2－1x 2－2 ＝y 1－1x 2－2＋y 2－1x 1－2x 1－2x 2－2＝12x 1＋m －1x 2－2＋12x 2＋m －1x 1－2x 1－2x 2－2＝x 1x 2＋m ＋2x 1＋x 2－4m －1x 1－2x 2－2＝2m 2－4＋m －2－2m －4m －1x 1－2x 2－2＝2m 2－4－2m 2＋4m －4m ＋4x 1－2x 2－2＝0∴k 1＋k 2＝0故直线MA 、MB 与x 轴始终围成一个等腰三角形．22．(本小题满分12分)(2019·全国Ⅲ卷理，21)已知曲线C ：y ＝x 22，D 为直线y ＝－12上的动点，过D 作C 的两条切线，切点分别为A ，B .(1)证明：直线AB 过定点；(2)若以E ⎝ ⎛⎭⎪⎫0，52为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积．[解析] (1)证明：设D ⎝ ⎛⎭⎪⎫t ，－12，A (x 1，y 1)，则x 21＝2y 1.因为y ′＝x ，所以切线DA 的斜率为x 1，故y 1＋12x 1－t＝x 1.整理得2tx 1－2y 1＋1＝0.设B (x 2，y 2)，同理可得2tx 2－2y 2＋1＝0. 故直线AB 的方程为2tx －2y ＋1＝0.所以直线AB 过定点⎝ ⎛⎭⎪⎫0，12. (2)由(1)得直线AB 的方程为y ＝tx ＋12.由⎩⎪⎨⎪⎧y ＝tx ＋12，y ＝x22可得x 2－2tx －1＝0.于是x 1＋x 2＝2t ，x 1x 2＝－1，y 1＋y 2＝t (x 1＋x 2)＋1＝2t 2＋1，|AB |＝1＋t 2|x 1－x 2|＝1＋t 2×x 1＋x 22－4x 1x 2＝2(t 2＋1)．设d 1，d 2分别为点D ，E 到直线AB 的距离， 则d 1＝t 2＋1，d 2＝2t 2＋1.因此，四边形ADBE 的面积S ＝12|AB |(d 1＋d 2)＝(t 2＋3)t 2＋1.设M 为线段AB 的中点，则M ⎝ ⎛⎭⎪⎫t ，t 2＋12.因为EM →⊥AB →，而EM →＝(t ，t 2－2)，AB →与向量(1，t )平行， 所以t ＋(t 2－2)t ＝0，解得t ＝0或t ＝±1. 当t ＝0时，S ＝3；当t ＝±1时，S ＝4 2. 因此，四边形ADBE 的面积为3或4 2.。

高中数学学业水平测试与课程标准（内容标准）的一致性
一、 绪论
1. 研究背景
2. 研究目的及意义
3研究方法
文献综述法，比较法，个案研究法、统计法、内容分析法
二、文献综述
2.1相关概念界定
课程标准、学业成就评价、高中学业水平测试、一致性
2.2外国一致性研究
2.3国内相关研究
三、研究过程
3.1研究对象
3.2确定研究模式
3.3内容维度的确定
3.4课标内容维度和认知维度二维表
3.5试题内容维度和认知维度二维表
3.6计算各试卷一致性p 值显著性p 值
2|
Yi Xi |-1=p ∑
n 1=i
四、数据分析结论
4.1高中数学学业水平测试与课标总体上的一致性
4.3知识深度一致性
4.4知识分布平衡性
五、结论
六、论文不足之处及建议。

高中数学教学中的教学质量评估数学是一门重要且广泛应用的学科，对高中学生的发展至关重要。

而教学质量评估是确保教育系统高效运行的关键环节之一。

本文将探讨在高中数学教学中进行教学质量评估的重要性、评估的方法和实施过程，以及如何利用评估结果改进教学质量。

一、教学质量评估的重要性教学质量评估是指对教师的教学过程和教学效果进行科学、客观、综合评价的过程。

它能够帮助教育管理者、教师和学生了解教学的有效性、教学目标的实现程度，从而提供依据改进教学质量的重要数据。

首先，教学质量评估能够帮助教师了解自身的教学水平和教学效果。

通过定期的评估，教师可以了解学生对教学内容的掌握情况和学生的学习能力，并可以及时对教学过程进行调整和优化，提高教学效果。

其次，教学质量评估有助于学生的学习和发展。

通过评估，教师可以发现学生的学习困难和需要改进的方面，针对性地提供帮助和指导，促进学生良好的学习与发展。

最后，教学质量评估是保证整个教育系统高效运行的重要手段。

通过评估结果，教育管理者可以了解学校的教学质量、教师的教学水平和教学资源的利用情况，以便制定相应的改进措施和政策。

二、教学质量评估的方法和实施过程1. 评估的方法高中数学教学质量评估可以采用多种方法，包括考试评估、作业评估、课堂观察和学生评价等。

考试评估是最常用的评估方法之一。

通过组织定期的考试，评估学生对知识的掌握程度和解题能力，从而了解教学进度和学生学习情况。

作业评估是对学生日常学习情况的评估方法。

老师可以通过批改学生的作业，了解学生对知识的理解和应用情况，及时发现问题并进行教学反馈。

课堂观察是对教师教学过程的评估方法。

相关教育管理者或教师同行可以进行课堂观察，对教师的讲解方式、教学方法和学生参与情况进行评估。

学生评价是对教学质量进行全面评估的方法。

可以通过问卷调查或小组讨论等形式，征求学生对教学内容、教学方法和教师的评价，了解学生对教学的满意程度和建议意见。

2. 实施过程教学质量评估的实施过程应该包括以下几个阶段：（1）确定评估目标和内容：明确评估的目标和要评估的内容，确定评估的重点和重要指标。

“基于高中数学课标的教、学、评一致性实践研究”课题开题报告一、课题的核心概念及其界定1.核心概念.课程标准: 国家或地方教育行政部门制定并强制施行的一种行业标准, 它是对国家教育方针和教育目的的课程化解释, 它对某个阶段的学生所必须学习的课程性质、理念、内容、目标以及实施建议做出了纲领性规定, 是学校学科教、学、评的基本依据．课程标准都是按照学段、学科进行编写的, 因此课程标准是指所有学科课程标准的总和．本课题中所说的课程标准（简称课标）专指由中华人民共和国教育部统一编制的最新版《普通高中数学课程标准》.课标分解: 是指将课程标准中的内容标准具体细化为学期或模块目标、单元或课时目标. 课表分解的基本特点是将抽象的内容标准分解为具体可操作的教学目标, 将长时段需要达成的大目标分解到短时间如单元或课时可以达成的小目标, 将隐性的素质目标显化为可以观察和评价的行为目标. 如果把课标作为一级目标, 那么学期或模块目标可以叫做二级目标, 单元或课时目标可以称为三级目标.教、学、评的一致性: 指教师的教、学生的学以及对教与学的考核评价统辖在统一的标准之下, 三者具有高度的相关性．具体地讲, 就是教什么、学什么、考什么是一致的；怎么教、怎么学、怎么评是一致的；教到什么程度、学到什么程度、考到什么程度是一致的；教学设计、教学实施、教学效果是一致的．2.课题总界定.基于高中数学课标的教、学、评一致性实践研究：在现代课程理念的观照下, 从课程的视角观察教、学、评的全过程, 以现代教学理论、学习理论、评价理论为指导, 通过对高中数学课程标准的逐级分解, 形成以教学目标为依据的教学设计方案（包括制定目标、实施路径、实施方法、反馈练习）与教学评价方案, 并以六所高中校学生为研究样本, 对方案进行试点实践和效果评估, 进而指导全市高中数学的教学与研究工作, 全面提高全市高中数学教师的专业素养和课堂教学质量．二、对国内外相关领域研究成果的述评与国内现状的反思1.布卢姆教育目标分类学.1956年, 以美国著名的教育家、心理学家本杰明·布卢姆（1913.2-1999.9.）为代表的团队出版了《教育目标分类学, 第一分册: 认知领域》, 把认知领域的目标分为六个亚领域, 即知识、领会、运用、分析、综合和评价.1964年, 由克拉斯沃尔(D.R.Krathwohl)负责完成的《教育目标分类学, 第二分册: 情感领域》公诸于世. 他们提出情感行为的中心是价值（态度）、兴趣、爱好、欣赏. 依据价值内化的程度, 情感目标从低到高分为五级: 接受、反应、价值化、组织、价值与价值体系的性格化.1972年, 由哈罗（A. J. Harrow）负责完成的《教育目标分类学, 第三分册：动作技能领域》正式出版, 书中提出了以学龄前教育为视角的动作技能教学目标分类. 同年, 辛普森(E.J.Simpson)在《动作技能领域教育目标分类》中提出了以职业技术教育为视角的动作技能教学目标分类. 辛普森的技能目标分七级：知觉、定向(定势)、有指导的反应、机械动作、复杂的外显反应、适应、创新.20XX年, 以安德森（L.W.Anderson）为首的专家团队出版了《布卢姆教育目标分类学（修订版）》, 书中提出了四个基本问题:(1)学习问题：在有限的学校和课堂教学时间内, 什么值得学生学习？(2)教学问题: 如何计划和进行教学才能使大部分学生在高层次上进行学习？(3)测评问题: 如何选择或设计测评工具和程序才能提供学生学习情况的准确信息？(4)一致性问题: 如何确保目标、教学和测评彼此一致。

高中数学学习材料马鸣风萧萧*整理制作肇庆市中小学教学质量评估 2011—2012学年第一学期统一检测题高二数学（理科）一、选择题：本大题共8小题，每小题5分，满分40分. 在每小题给出的四个选项中，只有一项是符合题目要求的. 1．在空间中，下列命题正确的是A ．垂直于同一平面的两条直线平行B ．垂直于同一平面的两个平面平行C ．平行于同一直线的两个平面平行D ．平行直线的平行投影重合 2．下列是全称命题且是真命题的是A ．0,2>∈∀x R xB ．0,,22>+∈∀y x R y xC ．Q x Q x ∈∈∀2, D ．1,200>∈∃x Z x3．双曲线142522=-y x 的渐近线方程是 A ．x y 52±= B ．x y 25±= C ．x y 254±= D ．x y 425±= 4．命题“若a >-3，则a >-6”以及它的逆命题、否命题、逆否命题中，真命题的个数为A ．1B ．2C ．3D ．45．已知向量)0,1,1(=a ，)2,0,1(-=b ，且b a k +与b a -2互相垂直，则k 的值是A ．1B ．51 C ．53 D ．576．若焦点在x 轴上的椭圆1222=+k y x 的离心率为21，则实数k 等于A ．3B ．32 C ．38 D ．23 7．若圆02)1(222=-+-++m my x m y x 关于直线01=+-y x 对称，则实数m 的值为A ．-1或3B ．-1C ．3D ．不存在8．如图，某几何体的正视图、侧视图和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体体积为A ．34B ．32C ．4D ．2二、填空题：本大题共6小题，每小题5分，满分30分.9．用一个平面截半径为25的球，截面面积是225π，则球心到截面的距离为 ▲ . 10．若A （-2，3）、B （3，-2）、C （21，m ）三点共线，则m 值为 ▲ . 11．双曲线14222=-y x 的离心率等于 ▲ . 12．若动点P 在122+=x y 上，则点P 与点Q （0，-1）连线中点的轨迹方程是 ▲ .13．不等式0)1)((<++x x a 成立的一个充分而不必要条件是12-<<-x ，则a 的取值范围是 ▲ .14．如图，在梯形ABCD 中，AB //CD ，AB =4，CD =2. E 、F 分别为AD 、BC 上点，且EF =3， EF //AB ，则梯形ABFE 与梯形EFCD 的面积 比为 ▲ .2俯视图正视图侧视图232ABC DEF三、解答题：本大题共6小题，满分80分. 解答须写出文字说明、证明过程和演算步骤. 15．（本小题满分12分）求满足下列条件的直线的方程：（1）经过点A （3，2），且与直线4x +y -2=0平行；（2）经过点B （2，-3），且平行于过点M （1，2）和N （-1，-5）的直线； （3）经过点C （3，0），且与直线2x +y -5=0垂直.16．（本小题满分12分）如图，一个高为H 的三棱柱形容器中盛有水. 若侧面AA 1B 1B 水平放置时，液面恰好过AC 、BC 、A 1C 1、B 1C 1的中点E 、F 、E 1、F 1. 当底面ABC 水平放置时，液面高为多少？17．（本小题满分14分）求与x 轴相切，圆心在直线3x -y =0上，且被直线x -y =0截得的弦长为72的圆的方程.18．（本小题满分14分）如图，棱长为a 的正方体1111D C B A ABCD -中，M 、N 、E 、F 分别是A 1B 1、A 1D 1、B 1C 1、C 1D 1的中点.（1）求证：B 、D 、E 、F 四点共面； （2）求证：平面AMN //平面BEFD ； （3）求点A 1到平面AMN 的距离．19．（本小题满分14分）如图，在长方体ABCD —A 1B 1C 1D 1中，E 、F 分别是棱BC 、CC 1上的点，CF =AB =2CE ，AB :AD :AA 1=1:2:4.ABCA 1B 1C 1E F E 1F 1AB CD A 1B 1C 1EFMN A 1B1C 1D 1（1）求异面直线EF 与A 1D 所成角的余弦值； （2）证明：AF ⊥平面A 1ED ；（3）求二面角A 1—ED —F 的大小的正弦值．20．（本小题满分14分）已知F 1、F 2分别为椭圆C 1：)0(12222>>=+b a bx a y 的上、下焦点，其中F 1也是抛物线C 2：y x 42=的焦点，点M 是C 1与C 2在第二象限的交点，且35||1=MF . （1）求椭圆C 1的方程；（2）已知A （b ，0），B （0，a ），直线 y =kx （k >0）与椭圆C 1相交于E 、F 两点. 求四边形AEBF 面积的最大值.2011—2012学年第一学期统一检测题 高二数学（理科）参考答案及评分标准一、选择题 题号 1 2 3 4 5 6 7 8 答案 ACABDDCB二、填空题AB MOE F 1xy F9．20 10．2111．3 12．24x y = 13．（2，+∞） 14．7:5三、解答题15．（本小题满分12分）解：（1）由直线4x +y -2=0得直线的斜率为-4， （2分） 所以经过点A （3，2），且与直线4x +y -2=0平行的直线方程为y -2=-4(x -3)，即4x +y -14=0. （4分） （2）由已知，经过两点M （1，2）和N （-1，-5）的直线的斜率271125=----=k ， （6分）所以，经过点B （2，-3），且平行于MN 的直线方程为)2(273-=+x y ，即7x -2y -20=0. （8分） （3）由直线2x +y -5=0得直线的斜率为-2， （9分） 所以与直线2x +y -5=0垂直的直线的斜率为21. （10分） 所以，经过点C （3，0），且与直线2x +y -5=0垂直的直线方程为)3(21-=x y ，即x -2y -3=0. （12分）16．（本小题满分12分）解：当侧面AA 1B 1B 水平放置时，水的体积V 等于 四棱柱ABFE —A 1B 1F 1E 1的体积，H S V V ABFE ∙==梯形四棱柱. （3分）当底面ABC 水平放置时，设水面高为h ，则水的体积h S V ABC ∙=∆. （6分） 因为E 、F 为AC 、BC 的中点，所以ABC CEF S S ∆∆=41， 所以ABC ABFE S S ∆=43梯形. （8分） 由h S H S ABC ABFE ∙=∙∆梯形，即h S H S ABC ABC ∙=∙∆∆43，得H h 43=. （11分）故当底面ABC 水平放置时，液面高为H 43. （12分）ABCA 1B 1C 1E FE 1F 117．（本小题满分14分）解：设所求的圆的方程是)0()()(222>=-+-r r b y a x ， （2分）则圆心到直线x -y =0的距离为2||b a -， （4分）所以222)7()2||(+-=b a r ，即14)(222+-=b a r ① （6分）因为所求的圆与x 轴相切，所以22b r = ② （8分） 又因为所求圆心在直线3x -y =0上，所以3a -b =0 ③ （10分）联立①②③，解得⎪⎩⎪⎨⎧===,3,3,1r b a 或⎪⎩⎪⎨⎧=-=-=.3,3,1r b a （12分）故所求圆的方程为9)3()1(22=-+-y x 或9)3()1(22=+++y x . （14分）18．（本小题满分14分） （1）证明：如图，连接B 1D 1. 因为E 、F 为B 1C 1、C 1D 1的中点， 所以EF //B 1D 1. （2分） 又因为BD //B 1D 1，所以EF //BD . （3分） 故B 、D 、E 、F 四点共面. （4分） （2）证明：连接EN .因为M 、N 为A 1B 1、A 1D 1的中点，所以MN //B 1D 1.又EF //B 1D 1，所以MN / / EF . （5分） 因为EF ⊂平面BEFD ，所以MN //平面BEFD . （6分） 因为E 、N 为B 1C 1、A 1D 1的中点，所以EN //A 1B 1，且EN =A 1B 1. 又AB //A 1B 1，且AB =A 1B 1，所以NE / / AB ，且NE =AB .所以四边形ABEN 为平行四边行，故AN //BE . （7分） 因为BE ⊂平面BEFD ，所以AN //平面BEFD . （8分）ABCDA 1B 1C 1E FMN因为MN ⊂平面AMN ，AN ⊂平面AMN ，且MN ∩AN =N ，所以平面AMN //平面BEFD . （9分） （3）证明：设A 1到平面AMN 的距离为d . 在∆AMN 中，a a a AN AM 254122=+==，a a a MN 22414122=+=， 所以22283162452221a a a a S AMN =-⨯⨯=∆. （11分） 因为MN A A AMN A V V 11--=三棱锥三棱锥， （12分） 即a a d a ⨯⨯=⨯⨯2281318331， （13分） 解得3a d =,故A 1到平面AMN 的距离为3a. （14分）19．（本小题满分14分）解：以A 为原点，建立如图所示的空间直角坐标系． 设AB =1，依题意得A （0，0，0），A 1（0，0，4）， D （0，2，0），E （1，23，0），F （1，2，1）. （2分） （1）易得)1,21,0(=EF ，)4,2,0(1-=D A ． （3分）所以535225410||||,cos 111-=⨯-+=∙∙>=<D A EF D A EF D A EF ， （5分）故异面直线EF 与A 1D 所成角的余弦值为53． （6分） （2）易得)1,2,1(=AF ，)4,23,1(1-=E A ，)4,2,0(1-=D A . （7分） 因为04311=-+=∙E A AF ，04401=-+=∙D A AF ， （8分） 所以E A AF 1⊥，D A AF 1⊥. （9分） 又A 1E ⊂平面A 1ED ，A 1D ⊂平面A 1ED ，A 1E ∩A 1D = A 1，所以AF ⊥平面A 1ED ． （10分） （3）设平面EFD 的法向量为),,(z y x m =．ABCDEFA 1B 1C 1D 1x yz由)1,21,0(=EF ，)0,21,1(-=ED ，⎪⎩⎪⎨⎧=∙=∙,0,0m ED m EF得⎪⎪⎩⎪⎪⎨⎧=+-=+,021,021y x z y 解得⎩⎨⎧-=-=.2,z y z x不妨令1-=z , 得)1,2,1(-=m ． （11分） 由（2）可知，)1,2,1(=AF 为平面A 1ED 的一个法向量. （12分） 于是3266141||||,cos =⨯-+=∙∙>=<AF m AF m AF m ， （13分） 从而35,sin >=<AF m . 所以二面角A 1—ED —F 的大小的正弦值为35. （14分）20．（本小题满分14分）解：（1）设)0)(,(000<x y x M .由C 2：y x 42=，得F 1（0，1）. （1分）因为M 在抛物线C 2上，故0204y x =. ① （2分） 又35||1=MF ，则3510=+y . ② （3分） 解①②得⎪⎪⎩⎪⎪⎨⎧=-=.32,36200y x （4分） 因为点M 在椭圆上，故1)362()32(2222=-+b a ，即1389422=+ba ③ （5分） 又c =1，则122+=b a ④ （6分）AB MOEF 1xyF解③④得⎪⎩⎪⎨⎧==.3,422b a 故椭圆C 1的方程为13422=+x y . （7分） （2）不妨设),(11y x E ，),(22y x F ，且21x x <.将kx y =代入13422=+x y 中，可得431222+=k x ， （8分） 即4332212+=-=k x x ，所以4332212+=-=k k y y . （9分）由（1）可得2||,3||==OB OA . （10分）故四边形AEBF 的面积为22223232212221y x y x S S S AEF BEF +=⨯⨯+⨯⨯=+=∆∆. （11分） 所以43341324364334222++∙=+++=k kk k k S （12分） 因为k k 34432≥+，所以143342≤+k k. （13分） 所以62≤S ，当且仅当332=k 时，等号成立. 故四边形AEBF 面积的最大值为62. （14分）。

附录2 教学案例与评价案例本附录提供了一些案例，是为了帮助教师更好地理解课程标准的要求，特别是理解数学核心素养与内容、教学、评价、考试命题的关系，为教学、评价、考试命题。

案例按照标准中出现的顺序排列，有些案例是说明内容、教学、评价、考试命题中的一个问题，有些案例是说明两个或两个以上问题；有些案例体现某个数学核心素养，有些案例综合体现了几个数学学科核心素养，案例中素养表述的顺序反映了所体现素养的主次。

有些案例针对在教学过程中容易出现的一些问题，是为了帮助教师答疑解惑。

每一个案例前有简短说明，说明本案例针对的问题及其蕴含的数学核心素养，以及如何使用该案例。

案例1 借助一元二次函数，求解一元二次不等式【目的】学习用函数统一理解初中学过的函数、方程与不等式的联系，逐渐学会利用函数解决相关的数学问题，体会数学内容之间的联系，提升直观想象与数学运算素养。

【情境】基于不等式2(00)ax bx c a >≠++，给出相应函数图象，分析求解的程序。

【分析】以下在实数范围内进行讨论。

当一个问题有不同的解决方法时，需要对这些方法进行分析、比较，选择能够体现数学本质的、试用范围更广的方法。

求解一元二次不等式通常有两种基本方法，一种是代数方法，先对二次三项式进行因式分解，把一元二次不等式转化为一元一次不等式组，通过求解一元一次不等式组，得到一元二次不等式的解集；另一种是函数方法，借助一元二次函数图象的直观，得到求解一元二次不等式的通性通法。

后者是一种程序思想方法，具体分析如下，对于一元二次不等式20ax bx c ++>，根据系数的不同，一元二次函数2y ax bx c =++的图象与x 轴的位置关系可以分为六类，如图1所示。

用函数方法求解的程序为：通过系数a 的符号，判定函数图象开口方向，通过一元二次方程20ax bx c ++=根的判别式24b ac -，判定函数图象与x 轴的位置关系；通过计算方程的根得到不等式的解集。

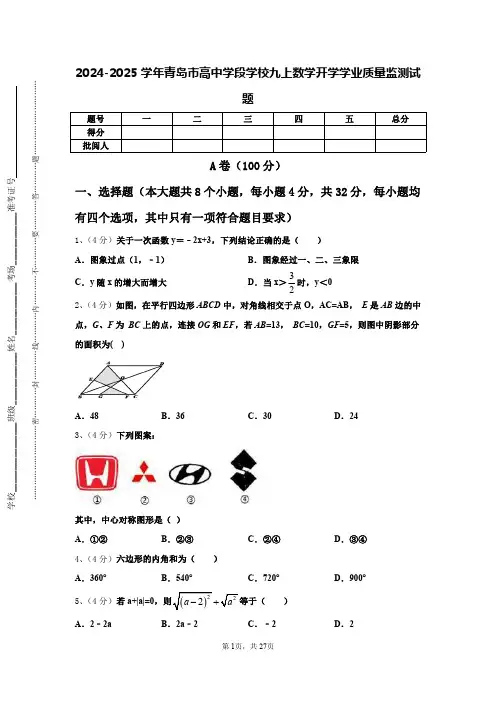
2024-2025学年青岛市高中学段学校九上数学开学学业质量监测试题题号一二三四五总分得分批阅人A 卷（100分）一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、（4分）关于一次函数y ＝﹣2x+3，下列结论正确的是（）A ．图象过点（1，﹣1）B ．图象经过一、二、三象限C ．y 随x 的增大而增大D ．当x ＞32时，y ＜02、（4分）如图，在平行四边形ABCD 中，对角线相交于点O ，AC=AB ，E 是AB 边的中点，G 、F 为BC 上的点，连接OG 和EF ，若AB =13，BC =10，GF =5，则图中阴影部分的面积为()A ．48B ．36C ．30D ．243、（4分）下列图案：其中，中心对称图形是（）A ．①②B ．②③C ．②④D ．③④4、（4分）六边形的内角和为（）A ．360°B ．540°C ．720°D ．900°5、（4分）若a+|a|=0）A ．2﹣2aB ．2a ﹣2C ．﹣2D ．26、（4分）四边形ABCD 中，AB ∥CD ，要使ABCD 是平行四边形，需要补充的一个条件（）A ．AD=BC B ．AB=CD C ．∠DAB=∠ABC D ．∠ABC=∠BCD7、（4分）若式子x 的取值范围是（）A ．0x >B ．1x >C ．1x ≥D ．1x ≤8、（4分）某灯泡厂为测量一批灯泡的使用寿命，从中抽查了100只灯泡，它们的使用寿命如表所示：使用寿命x/h 60≤x<100100≤x<140140≤x<180灯泡只数303040这批灯泡的平均使用寿命是（）A ．112h B ．124h C ．136h D ．148h 二、填空题（本大题共5个小题，每小题4分，共20分）9、（4分）如图，△ACE 是以ABCD 的对角线AC 为边的等边三角形，点C 与点E 关于x 轴对称．若E 点的坐标是（7，-，则D 点的坐标是_____．10、（4分）矩形的两条对角线的夹角为60，较短的边长为12cm ，则对角线长为________cm ．11、（4分）如图，二次函数2y ax bx c =++的图象过点A （3,0），对称轴为直线1x =，给出以下结论：①0abc <；②30a c +=；③2ax bx a b +≤+；④若M （-3，1y ）、N （6，2y ）为函数图象上的两点，则12y y <，其中正确的是____________．（只要填序号）12、（4分）某种药品原来售价100元，连续两次降价后售价为81元，若每次下降的百分率相同，则这个百分率是．13、（4分）小明用S 2=110[（x 1﹣3）2+（x 2﹣3）2+…+（x 10﹣3）2]计算一组数据的方差，那么x 1+x 2+x 3+…+x 10=______.三、解答题（本大题共5个小题，共48分）14、（12分）亮亮和颖颖住在同一幢住宅楼，两人准备用测量影子的方法测算其楼高，但恰逢阴天，于是两人商定改用下面方法：如图，亮亮蹲在地上，颖颖站在亮亮和楼之间，两人适当调整自己的位置，当楼的顶部M ，颖颖的头顶B 及亮亮的眼睛A 恰在一条直线上时，两人分别标定自己的位置C ，D ．然后测出两人之间的距离 1.25CD m =，颖颖与楼之间的距离30DN m =（C ，D ，N 在一条直线上），颖颖的身高1.6BD m =，亮亮蹲地观测时眼睛到地面的距离0.8AC m =．你能根据以上测量数据帮助他们求出住宅楼的高度吗？15、（8分）如图，直角坐标系中，一次函数的图象分别与，轴交于，两点，正比例函数的图象与交于点.（1）求的值及的解析式；（2）求的值；（3）一次函数的图象为，且，，不能围成三角形，直接写出的值.16、（8分）如图，边长为5的正方形OABC 的顶点O 在坐标原点处，点A ，C 分别在x 轴、y 轴的正半轴上，点E 是OA 边上的点(不与点A 重合)，EF ⊥CE ，且与正方形外角平分线AG 交于点P.(1)求证：CE=EP.(2)若点E 的坐标为(3，0)，在y 轴上是否存在点M ，使得四边形BMEP 是平行四边形?若存在，求出点M 的坐标；若不存在，说明理由.17、（10分）某小微企业为加快产业转型升级步伐，引进一批A ，B 两种型号的机器．已知一台A 型机器比一台B 型机器每小时多加工2个零件，且一台A 型机器加工80个零件与一台B 型机器加工60个零件所用时间相等．（1）每台A ，B 两种型号的机器每小时分别加工多少个零件？（2）如果该企业计划安排A ，B 两种型号的机器共10台一起加工一批该零件，为了如期完成任务，要求两种机器每小时加工的零件不少于72件，同时为了保障机器的正常运转，两种机器每小时加工的零件不能超过76件，那么A ，B 两种型号的机器可以各安排多少台？18、（10分）如图,在四边形ABCD 中,AB=AD=3,DC=4,∠A=60°，∠D=150°,试求BC 的长度.B 卷（50分）一、填空题（本大题共5个小题，每小题4分，共20分）19、（4分）如图,菱形ABCD 的对角线长分别为a、b,以菱形ABCD 各边的中点为顶点作矩形1111D C B A ,然后再以矩形1111D C B A 的中点为顶点作菱形2222A B C D ,……，如此下去,得到四边形A 2019B 2019C 2019D 2019的面积用含a,b 的代数式表示为___.20、（4分）如图，在平行四边形ABCD 中，AD=2AB,CE 平分BCD ∠交AD 于点E ，且3AE =，则平行四边形ABCD 的周长是____．21、（4分）若数a 使关于x 的不等式组1123522x x x x a-+⎧<⎪⎨⎪-≥+⎩有且只有四个整数解，a 的取值范围是__________．22、（4分）若a ，b 都是实数，b ＝﹣2，则a b 的值为_____．23、（4分）49的平方根为_______二、解答题（本大题共3个小题，共30分）24、（8分）解下列不等式组，并把它的解集表示在数轴上：315(1)468633x x x x +>-⎧⎪-⎨-≥⎪⎩25、（10分）如图，在△ABC 中，∠ACB=105°，AC 边上的垂直平分线交AB 边于点D ，交AC 边于点E ，连结CD ．（1）若AB=10，BC=6，求△BCD 的周长；（2）若AD=BC ，试求∠A 的度数．26、（12分）（定义学习）定义:如果四边形有一组对角为直角，那么我们称这样的四边形为“对直四边形”（判断尝试）在①梯形;②矩形:③菱形中，是“对直四边形”的是哪一个.(填序号)（操作探究）在菱形ABCD 中，2,60,AB B AE BC ︒=∠=⊥于点E,请在边AD 和CD 上各找一点F,使得以点A 、E 、C 、F 组成的四边形为“对直四边形”，画出示意图，并直接写出EF 的长，（实践应用）某加工厂有一批四边形板材，形状如图所示，若AB=3米，AD=1米，4590C A B ︒︒∠=∠=∠=.现根据客户要求，需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形"板材，且这两个等腰三角形的腰长相等，要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长，参考答案与详细解析一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、D 【解析】A、把点的坐标代入关系式，检验是否成立；B、根据系数的性质判断，或画出草图判断；C、根据一次项系数判断；D、可根据函数图象判断，亦可解不等式求解．解：A、当x=1时，y=1．所以图象不过（1，-1），故错误；B、∵-2＜0，3＞0，∴图象过一、二、四象限，故错误；C、∵-2＜0，∴y 随x 的增大而减小，故错误；D、画出草图．∵当x＞32时，图象在x 轴下方，∴y＜0，故正确．故选D．“点睛”本题主要考查了一次函数的性质以及一次函数与方程、不等式的关系．常采用数形结合的方法求解．2、C 【解析】连接EO ，设EF ，GO 交于点H ，过点H 作NM ⊥BC 与M ，交EO 于N ，过点A 作AP ⊥BC ，将阴影部分分割为△AEO ，△EHO ，△GHF ，分别求三个三角形的面积再相加即可．【详解】解：如图连接EO ，设EF ，GO 交于点H ，过点H 作NM ⊥BC 与M ，交EO 于N ，∵四边形ABCD 为平行四边形，O 为对角线交点，∴O 为AC 中点，又∵E 为AB 中点，∴EO 为三角形ABC 的中位线，∴EO ∥BC ，∴MN ⊥EO 且MN =12AP 即EO =5，∵AC =AB ，∴BP =PC 12BC =5，在Rt △APB 中，12AP ==，∴三角形AEO 的以EO 为底的高为12AP =6，MN =12AP =6∴16152AEO S EO =⨯=，11115551522222EHO GHF S S EO NH GF MH NH MH MN +=⨯+=⨯⨯+⨯⨯==，∴=30AEO EHO GHF S S S S ++=阴影,故选：C 本题考查了平行四边形的性质、三角形与四边形的面积关系；熟练掌握平行四边形的性质是解决问题的关键．3、D 【解析】试题分析：根据中心对称图形的概念：绕某点旋转180°，能够与原图形完全重合的图形．可知①不是中心对称图形；②不是中心对称图形；③是中心对称图形；④是中心对称图形．故选D ．考点：中心对称图形4、C 【解析】根据多边形内角和公式(n -2)×180º计算即可.【详解】根据多边形的内角和可得：（6﹣2）×180°=720°．故选C ．本题考查了多边形内角和的计算，熟记多边形内角和公式是解答本题的关键.5、A直接利用二次根式的性质化简得出答案．【详解】∵a+|a|=0，∴|a|=-a，则a≤0，故原式=2-a-a=2-2a．故选A．此题主要考查了二次根式的性质与化简，正确化简二次根式是解题关键．6、B【解析】根据平行四边形的判定方法一一判断即可．【详解】∵AB∥CD，∴只要满足AB=CD，可得四边形ABCD是平行四边形，故选：B．考查平行四边形的判定，解题的关键是熟练掌握基本知识，属于中考常考题型．7、C【解析】根据二次根式的被开方数是非负数列出不等式x-1≥0，通过解该不等式即可求得x的取值范围．【详解】解：根据题意，得x-1≥0，解得，x≥1．故选：C．8、B【解析】根据图表可知组中值，它们的顺序是80,120,160，然后再根据平均数的定义求出即可，平均数是指在一组数据中所有数据之和再除以数据的个数.【详解】解：这批灯泡的平均使用寿命是8030+12030+16040100⨯⨯⨯＝124（h ），故选B ．平均数在实际生活中的应用是本题的考点，解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数.二、填空题（本大题共5个小题，每小题4分，共20分）9、（3，0）【解析】∵点C 与点E 关于x 轴对称，E 点的坐标是（7，-，∴C 的坐标为（7，．∴CH=CE=∵△ACE 是以ABCD 的对角线AC 为边的等边三角形，∴AC=．∴AH=1．∵OH=7，∴AO=DH=2．∴OD=3．∴D 点的坐标是（3，0）．10、1【解析】分析：根据矩形对角线相等且互相平分性质和题中条件易得△AOB 为等边三角形，即可得到矩形对角线一半长，进而求解即可．详解：如图：AB ＝12cm ，∠AOB ＝60°．∵四边形是矩形，AC ，BD 是对角线．∴OA ＝OB ＝OD ＝OC ＝12BD ＝12AC ．在△AOB 中，OA ＝OB ，∠AOB ＝60°．∴OA ＝OB ＝AB ＝12cm ，BD ＝2OB ＝2×12＝1cm ．故答案为1．点睛：矩形的两对角线所夹的角为60°，那么对角线的一边和两条对角线的一半组成等边三角形．本题比较简单，根据矩形的性质解答即可．11、①②③【解析】①根据函数图像的开口、对称轴以及与y 轴的交点可得出a 、b 、c 的正负，即可判断正误；②根据函数对称轴可得出a 、b 之间的等量关系，将3+a c 转化为a b c -+，再由函数与x 轴的交点关于对称轴对称，可得出另一个交点是（-1,0），即可得出a b c -+的结果，即可判断正误；③根据a 、b 之间的等量关系，将不等式中的b 代换成a ，化简不等式即可判断正误；④根据开口向下的函数有最大值，距离顶点越近的函数值越大，先判断M 、N 距离顶点的距离即可判断两个点y 值得大小.【详解】解：①∵函数开口向下，∴a 0<,∵对称轴x 02b a =->,a 0<,∴b 0>；∵函数与y 轴交点在y 轴上半轴，∴c 0>，∴0abc <；所以①正确；②∵函数对称轴为x 12b a =-=，∴b 2a -=，∴3+=-+a c a b c ，∵A （3,0）是函数与x 轴交点，对称轴为x 1=，∴函数与x 轴另一交点为（-1,0）；∵当x 1=-时，0y a b c =-+=，∴30a c +=，②正确；③∵函数对称轴为x 12ba =-=，∴b 2a =-，∴将b 2a =-带入2ax bx a b +≤+可化为：222≤--ax x a a a ，∵a 0<，不等式左右两边同除a 需要不等号变方向，可得：2210x x -+≥，即()210x -≥，此不等式一定成立，所以③正确；④M （-3，1y ）、N （6，2y ）为函数图象上的两点，∵点M 距离顶点4个单位长度，N 点距离顶点5个单位长度，函数开口向下，距离顶点越近，函数值越大，∴12y y >，所以④错误.故答案为①②③.本题考查二次函数图像与系数的关系，可通过开口判断a 的正负，再根据对称轴可判断a 、b 的关系，即“左同右异”，根据函数与y 轴交点的正负可判断c 的正负；根据对称轴的具体值可得出a 、b 之间的等量关系；在比较函数值大小的时候，开口向下的二次函数上的点距离顶点越近，函数值越大即可判断函数值大小.12、10%．【解析】设平均每次降价的百分率为x ，那么第一次降价后的售价是原来的()1x -，那么第二次降价后的售价是原来的()21x -，根据题意列方程解答即可.【详解】设平均每次降价的百分率为x ，根据题意列方程得，()2100181x ⨯-=，解得10.110%x ==，2 1.9x =（不符合题意，舍去），答：这个百分率是10%.故答案为10%.本题考查一元二次方程的应用，要掌握求平均变化率的方法.若设变化前的量为a ，变化后的量为b ，平均变化率为x ，则经过两次变化后的数量关系为()21a x b ±=.13、30【解析】根据计算方差的公式能够确定数据的个数和平均数，从而求得所有数据的和.【详解】解：∵S 2=110[（x 1﹣3）2+（x 2﹣3）2+…+（x 10﹣3）2]，∴平均数为3，共10个数据，∴x 1+x 2+x 3+…+x 10=10×3=30.故答案为30.本题考查了方差的知识，牢记方差公式是解答本题的关键，难度不大.三、解答题（本大题共5个小题，共48分）14、20.8m ．【解析】试题分析：过A 作CN 的平行线交BD 于E ，交MN 于F ，由相似三角形的判定定理得出△ABE ∽△AMF ，再由相似三角形的对应边成比例即可得出MF 的长，进而得出结论．试题解析：过A 作CN 的平行线交BD 于E ，交MN 于F ．由已知可得FN=ED=AC=0.8m ，AE=CD=1.25m ，EF=DN=30m ，∠AEB=∠AFM=90°．又∵∠BAE=∠MAF ，∴△ABE ∽△AMF ．∴BE AE MF AF =，即：1.60.81.251.2530MF -=+，解得MF=20m ．∴MN=MF+FN=20+0.8=20.8m ．∴住宅楼的高度为20.8m ．考点:相似三角形的应用.15、（1）；（2）4；（3）或2或.【解析】（1）先求得点的坐标，再运用待定系数法即可得到的解析式；（2）过作于，于，则，，再根据，，可得，，进而得出的值；（3）分三种情况：当经过点时，；当，平行时，；当，平行时，；故的值为或2或．【详解】解：（1）把代入一次函数，可得，解得，，设的解析式为，则，解得，的解析式为；（2）如图，过作于，于，则，，，令，则；令，则，，，，，；（3）一次函数的图象为，且，，不能围成三角形，当经过点时，；当，平行时，；当，平行时，；故的值为或2或．本题主要考查一次函数的综合应用，解决问题的关键是掌握待定系数法求函数解析式、等腰直角三形的性质、全等三角形的判定和性质、勾股定理及分类讨论思想等．16、（1）证明见解析；（2）存在点M的坐标为(0，2).【解析】分析：（1）在OC上截取OK=OE．连接EK，求出∠KCE=∠CEA，根据ASA推出△CKE≌△EAP，根据全等三角形的性质得出即可；（2）过点B作BM∥PE交y轴于点M，根据ASA推出△BCM≌△COE，根据全等三角形的性质得出BM=CE，求出BM=EP．根据平行四边形的判定得出四边形BMEP是平行四边形，即可求出答案．详解：（1）在OC上截取OK=OE．连接EK，如图1．∵OC=OA，∠COA=∠BA0=90°，∠OEK=∠OKE=45°．∵AP 为正方形OCBA 的外角平分线，∴∠BAP =45°，∴∠EKC =∠PAE =135°，∴CK =EA ．∵EC ⊥EP ，∴∠CEF =∠COE =90°，∴∠CEO +∠KCE =90°，∠CEO +∠PEA =90°，∴∠KCE =∠CEA ．在△CKE 和△EAP 中，∵KCE PEA CK EA CKE EAP ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△CKE ≌△EAP ，∴EC =EP ；（2）y 轴上存在点M ，使得四边形BMEP 是平行四边形．如图，过点B 作BM ∥PE 交y 轴于点M ，连接BP ，EM ，如图2，则∠CQB =∠CEP =90°，所以∠OCE =∠CBQ ．在△BCM 和△COE 中，∵CBM OCE BC OC BCMCOE ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△BCM ≌△COE ，∴BM =CE ．∵CE =EP ，∴BM =EP ．∵BM ∥EP ，∴四边形BMEP 是平行四边形．∵△BCM ≌△COE ，∴CM =OE =3，∴OM =CO ﹣CM =2．故点M 的坐标为（0，2）．点睛：本题考查了正方形的性质，全等三角形的性质和判定，平行四边形的性质和判定的应用，能灵活运用知识点进行推理是解答此题的关键，综合性比较强，难度偏大．17、（1）每台A 型机器每小时加工8个零件，每台B 型机器每小时加工6个零件；（2）共有三种安排方案，方案一：A 型机器安排6台，B 型机器安排4台；方案二：A 型机器安排7台，B 型机器安排3台；方案三：A 型机器安排8台，B 型机器安排2台．【解析】(1)设每台B 型机器每小时加工x 个零件，则每台A 型机器每小时加工(x+2)个零件，根据工作时间=工作总量÷工作效率结合一台A 型机器加工80个零件与一台B 型机器加工60个零件所用时间相等，即可得出关于x 的分式方程，解之经检验后即可得出结论；(2)设A 型机器安排m 台，则B 型机器安排(10m)-台，根据每小时加工零件的总量8A =⨯型机器的数量6B +⨯型机器的数量结合每小时加工的零件不少于72件且不能超过76件，即可得出关于m 的一元一次不等式组，解之即可得出m 的取值范围，再结合m 为正整数即可得出各安排方案．【详解】(1)设每台B 型机器每小时加工x 个零件，则每台A 型机器每小时加工(x+2)个零件，依题意，得：8060x 2x =+，解得：x=6，经检验，x=6是原方程的解，且符合题意，x 28∴+=．答：每台A 型机器每小时加工8个零件，每台B 型机器每小时加工6个零件；(2)设A 型机器安排m 台，则B 型机器安排(10m)-台，依题意，得：()()861072861076m m m π⎧+-⎪⎨+-⎪⎩ ，解得：6m 8 ，m 为正整数，m 678∴=、、，答：共有三种安排方案，方案一：A 型机器安排6台，B 型机器安排4台；方案二：A 型机器安排7台，B 型机器安排3台；方案三：A 型机器安排8台，B 型机器安排2台．本题考查了分式方程的应用以及一元一次不等式组的应用，解题的关键是：(1)找准等量关系，正确列出分式方程；(2)根据各数量之间的关系，正确列出一元一次不等式组．18、5BC =【解析】试题分析：连接DB，根据AB=AD，∠A=60°得出等边三角形，根据等边三角形的性质以及∠ADC=150°得出△BDC 为直角三角形，最后根据勾股定理求出BC 的长度.试题解析：连结DB ,∵AB AD =，60A ∠=︒，∴ABD 是等边三角形，∴3BD AD ==，60ADB ∠=︒，又∵150ADC ∠=︒∴1506090CDB ADC ADB ∠=∠-∠=︒-︒=︒，∵4,DC =∴5BC ===一、填空题（本大题共5个小题，每小题4分，共20分）19、202012ab 【解析】根据三角形中位线定理，逐步得到小长方形的面积，得到规律即可求解.【详解】∵菱形ABCD 的对角线长分别为a 、b ，AC ⊥BD ，∴S 四边形ABCD=12ab ∵以菱形ABCD 各边的中点为顶点作矩形1111D C B A ,根据中位线的性质可知S 四边形A 1B 1C 1D 1=12S 四边形ABCD=14ab …则S 四边形A n B n C n D n =12n S 四边形ABCD=112n ab +故四边形A 2019B 2019C 2019D 2019的面积用含a,b 的代数式表示为202012ab .故填：202012ab .此题主要考查特殊平行四边形的性质，解题的关键是根据题意找到规律进行求解.20、18【解析】利用平行四边形的对边相等且互相平行,进而得出AE=DE=AB,再求出ABCD 的周长【详解】∵CE 平分∠BCD 交AD 边于点E,∴.∠ECD=∠ECB∵在平行四边形ABCD 中、AD ∥BC,AB=CD ，AD=BC ∴∠DEC=∠ECB,∴∠DEC=∠DCE ∴DE=DC ∵AD=2AB ∴AD=2CD ∴AE=DE=AB=3∴AD=6∴四边形ABCD 的周长为:2×(3+6)=18.故答案为:18.此题考查平行四边形的性质，解题关键在于利用平行四边形的对边相等且互相平行21、112α-<≤-【解析】此题可先根据一元一次不等式组解出x 的取值，再根据不等式组1123522x x x x a -+⎧<⎪⎨⎪-≥+⎩恰好只有四个整数解，求出实数a 的取值范围．【详解】1123522x x x x a -+⎧<⎪⎨⎪-≥+⎩①②解不等式①得，x ＜5，解不等式②得，x≥2+2a ，由上可得2+2a≤x ＜5，∵不等式组1123522x xx x a-+⎧<⎪⎨⎪-≥+⎩恰好只有四个整数解，即1，2，3，4；∴0＜2+2a≤1，解得，112a -<-≤.此题考查的是一元一次不等式的解法和一元一次方程的解，根据x 的取值范围，得出x 的取值范围，然后根据不等式组1123522x x x x a -+⎧<⎪⎨⎪-≥+⎩恰好只有四个整数解即可解出a 的取值范围．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．22、1【解析】直接利用二次根式有意义的条件得出a 的值，进而利用负指数幂的性质得出答案．【详解】解：∵b ﹣2，∴120210a a -≥⎧⎨-≥⎩∴1-2a=0，解得：a=12，则b=-2，故a b =（12）-2=1．故答案为1．此题主要考查了二次根式有意义的条件，以及负指数幂的性质，正确得出a 的值是解题关键．23、23±【解析】利用平方根立方根定义计算即可．【详解】∵224=39⎛⎫± ⎪⎝⎭，∴49的平方根是±23，故答案为±23.本题考查了方根的定义，熟练掌握平方根的定义是解本题的关键.注意：区别平方根和算术平方根．一个非负数的平方根有两个，互为相反数，正值为算术平方根．二、解答题（本大题共3个小题，共30分）24、原不等式组的解集为2≤x ＜1,表示见解析.【解析】先求出每个不等式的解集，再根据找不等式组解集的规律找出不等式组的解集即可．【详解】解：解不等式1x +1＞5（x ﹣1），得：x ＜1，解不等式43x ﹣6≥683x ，得：x ≥2，在同一条数轴上表示不等式的解集为：所以原不等式组的解集为2≤x ＜1．本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．25、（1）16；（2）25°．【解析】根据线段垂直平分线的性质，可得CD=AD ，根据三角形的周长公式，可得答案；根据线段垂直平分线的性质，可得CD=AD ，根据等腰三角形的性质，可得∠B 与∠CDB 的关系，根据三角形外角的性质，可得∠CDB 与∠A 的关系，根据三角形内角和定理，可得答案．【详解】解：（1）∵DE 是AC 的垂直平分线，∴AD=CD ．∵C △BCD =BC+BD+CD=BC+BD+AD=BC+AB ，又∵AB=10，BC=6，∴C△BCD =16；（2）∵AD=CD ∴∠A=∠ACD ，设∠A=x ，∵AD=CB ，∴CD=CB ，∴∠CDB=∠CBD ．∵∠CDB 是△ACD 的外角，∴∠CDB=∠A+∠ACD=2x ，∵∠A 、∠B 、∠ACB 是三角形的内角，∵∠A+∠B+∠ACB=180°，∴x+2x+105°=180°，解得x=25°∴∠A=25°．本题考查线段垂直平分线的性质．26、【判断尝试】②；【操作探究】EF 的长为2，EF 【实践应用】方案1：两个等腰三角形的腰长都为322米．理由见解析，方案2：两个等腰三角形的腰长都为2米．理由见解析，方案34：两个等腰三角形的腰长都为22米，理由见解析．【解析】[判断尝试]根据“对直四边形”定义和①梯形;②矩形:③菱形的性质逐一分析即可解答.[操作探究]由菱形性质和30°直角三角形性质即可求得EF 的长.[实践应用]先作出“对直四边形”，容易得到另两个等腰三角形，再利用等腰三角形性质和勾股定理即可求出腰长.【详解】解：[判断尝试]①梯形不可能一组对角为直角;③菱形中只有正方形的一组对角为直角，②矩形四个角都是直角，故矩形有一组对角为直角，为“对直四边形”，故答案为②，[操作探究]F 在边AD 上时，如图：∴四边形AECF 是矩形，∴AE=CE ，又∵2,60,AB B AE BC ︒=∠=⊥，∴BE=1，AE=，CE=AF=1，∴在Rt △AEF 中，=2EF 的长为2.F 在边CD 上时，AF ⊥CD ，∵四边形ABCD 是菱形，∴AB=AD=2，∠B=∠D=60°，又∵AE ⊥BC ，∴∠BAE=∠BAF=30°，∴，∵∠BAD=120°，∴∠EAF=60°，∴△AEF 为等边三角形，∴即：EF故答案为2.[实践应用]方案1：如图①，作DE BC,EF CD ⊥⊥，则四边形ABCD 分为等腰FED 、等腰FEC 、“对直四边形”ABED ，其中两个等腰三角形的腰长都为322米．理由：∵A B 90︒∠=∠=，∴四边形ABED 为矩形，∴DE AB ==3米，∵C 45︒∠=，∴△DEC 为等腰直角三角形，∴DE=EC=3米，∴DC=米，∵EF CD ⊥，∴FD FE FC ===12DC=2米．方案2：如图②，作BE DC,EF BC ⊥⊥，则四边形ABCD 分为等腰△FEB 、等腰△FEC 、“对直四边形”ABED ，其中两个等腰三角形的腰长都为2米．理由：作DG BC ⊥，由（1）可知DG AB GC ===3米，BG=AD=1米，∴BC=1+3=4米，∵C 45,BE DC ︒∠=⊥，∴△BEC 为等腰直角三角形，∵EF BC ⊥，∴FE FB FC ===12BC=2米．方案3：如图③，作CD 、BC 的垂直平分线交于点E ，连接ED 、EB ，则四边形ABCD 分为等腰△CED 、等腰△CEB 、“对直四边形”ABED 理由：连接CE ，并延长交AB 于点F ，∵CD 、BC 的垂直平分线交于点E ，∴ED EC EB ==，∴12,34∠=∠∠=∠，∴DEB 65123421232(13)∠=∠+∠=∠+∠+∠+∠=∠+∠=∠+∠2DCB 24590︒︒=-∠=-⨯=-．连接DB ，，∵ED=EB ，∴△BED 为等腰直角三角形，∴∴ED EC EB ===方案4：如图④，作DE DC ⊥，交AB 于点E ，AF DE ⊥，则四边形ABCD 分为等腰△AFE 、等腰△AFD 、“对直四边形”BEDC ，其中两个等腰三角形的腰长都为2米．理由：作DE DC ⊥，交AB 于点E ，可证∠ADE =45°，∵DAE 90︒∠=，∴△ADE 为等腰直角三角形，∴DE 米，作AF DE ⊥，∴FE FD FA ===12DE=2米．此题是四边形综合题，主要考查了新定义“对直四边形”的理解和应用，矩形的判定和性质，勾股定理，正确作出图形是解本题的关键．。

基于学业质量标准的单个试题的命制与评价作者：孔德鹏来源：《江苏教育·中学教学》 2020年第1期孔德鹏【摘要】学业质量标准反映了2017年版高中数学课程标准的最新成果，是学生学习数学课程后学业成就的表现。

基于学业质量标准对单个试题的命制与评价进行探讨，从单个试题命制的背景与过程、单个试题评价以及数学关键能力赋分等角度展开，反思命题评价：命制试题离不开知识，忌空谈素养；评价要凸显过程性，遵循素养达成规律；评价要注重“双原则”，创新评价形式。

【关键词】学业质量；试题命制；数学核心素养【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009（2020）03-0019-04【作者简介】孔德鹏，南京航空航天大学附属高级中学（南京，210007）教师，一级教师。

《普通高中数学课程标准（2017年版）》（以下简称“2017年版课标”）明确了学业质量标准，强调以数学核心素养及其表现为主要维度，对学生学业成就表现进行总体刻画。

［1］另外，2017年版课标在“评价建议”中要求教师重视整体性评价和过程性评价，革新评价方式，注重评价的主体多元化、评价形式的多样化。

数学核心素养的发展过程是循序渐进的，具有阶段性、连续性和整合性等特点，这就意味着命题评价要体现过程性和阶段性，不仅要关注素养水平实际情况，更要关注学生成长和发展的过程，关注学生在学习过程中的发展和变化。

单个试题命制是整张试卷命制的基础，值得关注与研究。

笔者就如何进行素养导向的试题命制和如何注重发展学生数学素养的过程评价进行了积极探索。

一、单个试题命制的背景和过程按照南京市课程教学计划，高一下学期的主题内容包括三角变换、解三角形、立体几何与解析几何初步。

期中考试的基本定位为阶段性学业质量检测，涉及内容为三角变换、解三角形、立体几何等有关知识。

就数学学科核心素养评价而言，笔者认为应用题可以重点评价考生的数学抽象、数学建模、直观想象、数学运算等核心素养水平。

基于课程标准的试题评价探讨作者：***来源：《中学数学杂志(高中版)》2021年第04期【摘要】基于數学核心素养的试题评价，应创新评价的形式和方法，借助SOLO分类理论，把知识技能的评价与数学学科核心素养达成状况的评价有机融合，不仅能更好地体现学生在某一阶段和某一内容的学习上对知识的掌握程度和认知水平，也有助于教师更多地关注在试题讲评中对学生把握数学学习规律的过程评价.【关键词】试题评价;SOLO理论;核心素养《普通高中数学课程标准（2017年版2020年修订）》（以下简称课标）指出，教学评价要以数学学科核心素养的达成作为评价的基本要素[1].因此，作为教学质量监测形式之一的试题评价，也要创新评价的形式和方法，把知识技能的评价与数学学科核心素养达成状况的评价有机融合，体现课标中提出的学业质量的要求，从而落实立德树人根本任务.本文以一道高三区域监测试题为例，尝试相关探究.1 试题评价的重要参考依据——多维双向细目表课标要求，学业水平测试的命题要以学业要求的达成为目标，以核心知识为基础、以问题情境为载体、以思想方法为依托，以关键能力为特征，综合体现数学核心素养的落实;《中国高考评价体系》指出，高考“四翼”包括基础性、综合性、应用性、创新性，回答了高考“怎么考”的问题.因此作为体现课程标准和高考“四翼”的多维双向细目表，是高三模拟试题命制必须要遵循的框架，也是试题分析时必须参考的依据，更是试题评价不可回避的重要组成部分.然而很多情况下，它只在试题命制时受到重视.下表就是本文要讨论的这道试题的多维双向细目表.通过对试题中核心素养的水平划分，教师能更好地把握学生在例1监测结果中所处的能力层次，聚焦核心素养的达成情况，而不是在试题讲解和分析中过于片面地注重试题得分情况、简单地错因归纳等情形.4 结语基于数学核心素养的试题评价，不同于试题的评分判定，并不是根据特定的“给分点”给出固定分数，其更有助于全体学生在具体内容中了解自己的真实水平，分析存在的问题，更有助于整体把握和调整“教师的教和学生的学”.通过从构建数学核心素养评价维度的角度，理解试题评价中核心素养的水平层次划分结果，能更好地体现学生在某一阶段和某一内容的学习上对知识的掌握程度和认知水平，也有助于教师更多地关注在试题讲评中对学生把握数学学习规律的过程评价.参考文献[1]教育部.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020.[2]翟凤琦.基于SOLO分类理论的数学逻辑推理素养水平划分研究[D]. 沈阳：辽宁师范大学，2019：32-35.作者简介周威（1985—），男，湖南邵阳人，研究生学历，中学一级教师，研究方向：中学数学教育与质量监测评价.。

新课标教学评价与考试命题教案《新课标教学评价与考试命题教案》这是优秀的教学设计文章，希望可以对您的学习工作中带来帮助！作业内容高中数学课程标准2017版将数学核心素养按照“情境与问题、知识与技能、思维与表达、交流与反思”四个纬度，给出了相应的水平标准，明确了学生完成高中数学学业后其数学核心素养应达到的相应水平。

这里的学业质量标准旨在引导教学更加关注育人目的，更加注重学生核心素养之培养，更加强调提高学生综合运用知识发现、提出问题并加以分析、解决问题的实际能力，帮助教师和学生把握教与学的深度、广度，为日常的阶段性评价、学业水平考试和升学考试命题提供重要依据，促进教、学、考的有机衔接，进而形成育人合力。

给出相对明确的学业质量标准，是高中数学课程标准2017版的亮点之一。

(6)增强了指导性和实践操作性与实验稿相比，高中数学课程标准2017版进一步提升了课程标准的实践操作性，凸显课程标准对教材研制开发、课程教学实施、数学考试评价的指导作用。

例如，与实验稿相比，高中数学课程标准2017版增加了“学业质量水平与考试评价的关系”，明确数学学业质量水平一、二、三的功能、作用，即数学学业质量水平是六个数学核心素养水平的综合表现。

数学学业质量水平一是高中毕业应当达到的要求，也是高中毕业的数学学业水平考试的命题。

数学学业质量水平二是高考的要求，也是数学高考的命题依据;数学学业质量水平三是基于必修、选择性必修和选修课程的某些内容对数学核心素养的达成提出的要求，可以作为大学自主招生的参考。

与实验稿相比，高中数学课程标准2017版逻辑更清晰、语言更通俗易懂，每个模块或主题原则上由“内容要求”“教学提示”“学业要求”组成，并增加了教学与评价案例，同时依据学业质量标准细化评价目标，强化了对教学和评价的指导性。

构建了新的高中数学教育理念高中数学课程标准2017版从国际意识、时代需求、国民素质、个性发展等方面的综合思考，构建了高中数学课程新的教育观、课程观、教学观。