八年级上册数学同步培优:第9讲 乘法公式 平方差公式--基础班
- 格式:docx
- 大小:103.92 KB
- 文档页数:6



![人教版数学八年级上册平方差公式PPT精品课件[1]](https://img.taocdn.com/s1/m/27a178f1482fb4daa48d4bcb.png)

第9讲乘法公式一平方差公式知识点1 平方差公式22+-=-a b a b a b()()平方差公式的特点:两个数的和与这两个数的差的积,等于这两个数的平方差.在利用平方差公式进行计算时,先判断式子能否利用平方差公式计算,如果可以,再根据22a b a b a b+-=-进行乘法计算.()()【典例】1.下列多项式乘法中可以用平方差公式计算的是()A. (﹣a+b)(a﹣b)B. (x+2)(2+x)C. (+y)(y﹣)D. (x﹣2)(x+1)【方法总结】平方差公式的特点:即两数和与它们差的积等于这两数的平方差.也就是说,左边是两个二项式相乘,这两项中有一项完全相同,另一项互为相反数.2.计算(x﹣2y+1)(x+2y﹣1)时,下列变形中正确的是()A. [x﹣(2y+1)][x+(2y+1)]B. [x﹣(2y﹣1)][x+(2y﹣1)]C. [(x﹣2y)+1][(x﹣2y)﹣1]D. [(x+1)﹣2y][(x+1)+2y]【方法总结】平方差公式一般是两数的和与它们的差的积等于这两数的平方差,但这里边的a和b也可以用式子来表示,对于(a-b+c)(a+b-c)这类题而言,我们可以对两个括号内的式子进行变形,目的是拼凑出两个数(或式子)的和与差的乘积形式,观察易得出(a-b+c)(a+b-c)=[a-(b-c)][a+(b-c)],这样就变成了a与(b-c)的和与差的乘积,所以可得出(a-b+c)(a+b-c)=[a-(b-c)][a+(b-c)]=a2-(b-c)2然后再进行下一步计算.【随堂练习】1.(2017秋•禄劝县期末)计算:(2a+b)(b﹣2a)﹣(a﹣3b)22.(2018春•顺义区期末)计算:(2x﹣1)(2x+1)﹣(3﹣2x)2.3.(2017秋•利川市期末)计算(a﹣3b)(a+3b)﹣(﹣a﹣2b)(a﹣2b)知识点2 利用平方差公式进行数的运算在一些计算中,有时利用平方差公式,会使计算量大大减少;例如98×102,可以利用平方差公式化成98×102=(100-2)×(100+2)=100²-2²=9996.【典例】1.20132﹣2011×2015的计算结果是()A. 2B. ﹣2C. 4D. ﹣4【方法总结】此题主要考查了平方差公式,关键是掌握22a b a b a b+-=-()()本题直接计算,计算量很大,观察式子可以发现,题目中给出了20132,所以在对后面的式子进行变形时,尽量凑出2013,那么很容易得出2011=2013-2,2015=2013+2,再利用平方差公式2011×2015=(2013-2)×(2013+2),然后再计算即可.【随堂练习】1.(2018•河北模拟)请你参考黑板中老师的讲解,用乘法公式简便计算;(1)6992(2)20192﹣2017×20212.(2018•邯郸一模)张老师在黑板上写了三个算式,希望同学们认真观察,发现规律.请你结合这些算式,解答下列问题:请观察以下算式:①32﹣12=8×1②52﹣32=8×2③72﹣52=8×3(1)请你再写出另外两个符合上述规律的算式;(2)验证规律:设两个连续奇数为2n+1,2n﹣1(其中n为正整数),则它们的平方差是8的倍数;(3)拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?3.(2018春•抚州期末)阅读下面的材料并填空:①(1﹣)(1+)=1﹣,反过来,得1﹣=(1﹣)(1+)=②(1﹣)(1+)=1﹣,反过来,得1﹣=(1﹣)(1+)=×③(1﹣)(1+)=1﹣,反过来,得1﹣=(1﹣)(1+)=利用上面的材料中的方法和结论计算下题:(1﹣)(1﹣)(1﹣)……(1﹣)(1﹣)(1﹣)知识点3 利用平方差公式进行整式的运算【典例】1.如果(m+1+n)(m-1+n)=8,那么m+n的值为()A. ±9B. ±3C. 3D. 9【方法总结】通过上边的学习我们知道,对于这种两个三项式相乘,我们可以对两个三项式变形,使他们分别变成两个数(或式子)的和与差相乘的形式,然后再利用平方差公式进行下一步计算,除此之外需要注意,结果是两个数,二者互为相反数.【随堂练习】1.(2017春•泰兴市校级期中)计算:(1)(x﹣2)(x+3)﹣(x+3)2(2)(x﹣2y+4)(x﹣2y﹣4)2.(2017秋•普陀区校级期中)计算:(3x+y+1)(3x+y﹣1).知识点4 平方差公式—几何背景平方差公式的证明方法有很多种,其中几何法证明是最常见的一种,也是初中阶段最容易理解的一种.【典例】1.如图1,在边长为a的正方形中剪去一个边长为b的小正形(a>b),把剩下部分拼成一个梯形(如图2),利用这两幅图形面积,可以验证的公式是()A. (a+b)(a﹣b)=a2+b2B. (a+b)(a﹣b)=a2﹣b2C. (a+b)2=a2+2ab+b2D. (a﹣b)2=a2﹣2ab+b2【方法总结】本题考查了平方差公式的几何背景,认识不同表示方法之间的关系,解题的重要点是利用面积的不变性.【随堂练习】1.(2017春•高台县校级期末)乘法公式的探究及应用.(1)如图1可以求出阴影部分的面积是_____(写成两数平方差的形式);(2)如图2若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是____,长是____,面积是________(写成多项式乘法的形式);(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式_____ (用式子表达);(4)运用你所得到的公式,计算下列各题:①(2m+n﹣p)(2m﹣n+p)②10.3×9.7.2.(2017春•栾城区期末)(1)如图1,在边长为a的正方形中,画出两个长方形阴影,则阴影部分的面积是____(写成两数平方差的形式);(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的长是____,宽是______,面积是_________(写成多项式乘法的形式);(3)比较左、右两图的阴影部分面积,可以得到乘法公式_______(用式子表达);(4)运用你所得到的公式计算:①10.3×9.7②(2m+n﹣p)(2m﹣n+p)3.(2017秋•荔湾区校级期中)图1、图2分别由两个长方形拼成.(1)图1中图形的面积为a2﹣b2,图2中图形的面积为(a﹣b)×_____.(用含有a、b的代数式表示)(2)由(1)可以得到等式:__________.(3)根据你得到的等式解决下列问题:①计算:68.52﹣31.52.②若m+4n=2,求(m+1)2﹣m2+(2n+1)2﹣(2n﹣1)2的值.综合运用1.(x+2)(x﹣2)(x2+4)的计算结果是__________2.若(x﹣ay)(x+ay)=x2﹣16y2,则a=.3.(m+3)(m﹣3)=.4.计算:(﹣m+n)(﹣m﹣n)=.5.化简(a﹣1)(a+1)(a2+1)﹣(a4﹣1)的结果为___________6.计算20072﹣2006×2008得_______7.已知A=99×100×101,B=98×100×102,则A﹣B的值是___________8.计算(2x﹣3y+1)(2x+3y﹣1)的结果是_________9.如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是___________。
2019-2020年八年级数学上册14.2乘法公式14.2.1平方差公式教案新版新人教版教学目标:理解乘法的平方差公式,并能运用平方差公式进行简单的运算.重点:平方差公式的推导和应用.难点:理解平方差公式的结构特征,灵活应用平方差公式.教学流程:一、情境引入灰太狼开了一家租地公司,一天他把一边长为a米的正方形土地,租给慢羊羊种植,有一年,他对慢羊羊说,我把这块地的一边增加5米,另一边减少5米,再继续租给你,租金不变,这样你也没吃亏,你看如何,慢羊羊一听觉得没有吃亏,就答应了.慢羊羊回到羊村,就把这件事对喜羊羊他们讲了,喜羊羊一听马上说,“村长,您吃亏了!”慢羊羊村长很吃惊的问道:“啊,那我吃亏了多少?”沸羊羊说道:“我来帮您算算,”喜羊羊还没等沸羊羊开始算就说到:“不用算啦,村长亏了25平方米!”沸羊羊不解道:“你怎么算的这么快呀?”。
二、知识回顾1.说一说多项式乘以多项式的计算法则?答案:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.2.填空(1)(1)(1)________;(2)(2)(2)________;(3)(21)(21)________.x x m m x x +-=+-=+-=答案:(1);(2);(3)三、探究问题:观察下面等式,你能发现什么规律?222112222(1)()()1;(2)()()4;(3)()(1.1)41x m x x m m x x x +-=-+-=-+-=-归纳:乘法的平方差公式:两个数的和与这两个数的差的积,等于这两个数的平方差.图形演示:尝试计算:,解:222(1).(32)(32)(3)294x x x x +-=-=- 2222(2).(2)(2)()(2)4x y x y x y x y -+--=--=-练习:1.下列各式中,能用平方差公式计算的是( )A .(2x -3y )(-2x +3y )B .(-3x +4y )(-4y -3x )C .(x -y )(x +2y )D .(x +y )(-x -y )答案:B2.下面各式的计算对不对?如果不对,应当怎样改正?22222223232323222323294(1)()()(2)()()9(3)()()(4)()(49)4a a a a a a b a x x x b b x a a x x +-=--=+-=---=----答案:(1)√;(2)×;22222323()()46694129a b a b a ab ab b a ab b --=--+=-+(3)×,22222()()24x x x x +-=-=-(4)×,23232232349()()()()a a a a a ---=---+=- 3.计算:(2)(2)(1)(5);(2)1(02981).y y y y +---+⨯ 解:2222222(1)(2)(2)(1)(5)2(45)44541(2)10298(1002)(1002)10021000049996y y y y y y y y y y y +---+=--+-=---+=-+⨯=+-=-=-= 四、应用提高计算(x 4+1)(x 2+1)(x +1)(x -1)的结果是( )A.x 8+1B.x 8-1C.(x +1)8 D.(x -1)8答案:B提示: 42422448(1)(1)(1)(1)(1)(1)(1)(1)(1)1x x x x x x x x x x ===+++-++-+--五、体验收获今天我们学习了哪些知识?1.说一说乘法的平方差公式?2.应用平方差公式时要注意什么?六、达标测评1.下列计算正确的是( )A .(x +3)(x -3)=x 2-6B .(3x +2y )(3x -2y )=3x 2-2y 2C .(m -n )(-m -n )=m 2-n 2D .(34a +43b )(43b -34a )=169b 2-916a 2答案:D2.如图①,在边长为a 的正方形纸片中剪去一个边长为b 的小正方形(a >b ),把剩下的部分拼成一个梯形(如图②),利用这两个图形的面积,可以验证的公式是( )A.a 2+b 2=(a +b )(a -b )B.a 2-b 2=(a +b )(a -b )C.(a +b )2=a 2+2ab +b2 D.(a -b )2=a 2-2ab +b 2答案:B 3.计算:()1911119(222()()(3)(3)55)p q s q t t s p ---+-; 解: 2222(1)(911)(119)(119)(119)(11)(9)12181s t t s t s t s t s t s ==-=-+-+-222222(2)(3)(3)5522(3)(3)552()(3)54925p q p q q p q p q p q p ---=-+--=--=- 4.先化简,再求值:a (3-a )-(1-a )(1+a ).2222(3)(1)(1)3(1)3131a a a a a a a a a aa ---+=---=--+=-解:当a =2时,原式=3×2-1=5.七、布置作业教材108页练习题第2题.`27735 6C57 汗25502 639E 掞32284 7E1C 縜25949 655D 敝24778 60CA 惊32200 7DC8 緈O"29605 73A5 玥221037 522D 刭22377 5769 坩34432 8680 蚀。
第9讲乘法公式一平方差公式
知识点1 平方差公式
22
+-=-
a b a b a b
()()
平方差公式的特点:两个数的和与这两个数的差的积,等于这两个数的平方差.
在利用平方差公式进行计算时,先判断式子能否利用平方差公式计算,如果可以,再根据22
+-=-进行乘法计算.
a b a b a b
()()
【典例】
1.下列多项式乘法中可以用平方差公式计算的是()
A. (﹣a+b)(a﹣b)
B. (x+2)(2+x)
C. (+y)(y﹣)
D. (x﹣2)(x+1)【方法总结】
平方差公式的特点:即两数和与它们差的积等于这两数的平方差.也就是说,左边是两个二项式相乘,这两项中有一项完全相同,另一项互为相反数.
2.计算(x﹣2y+1)(x+2y﹣1)时,下列变形中正确的是()
A. [x﹣(2y+1)][x+(2y+1)]
B. [x﹣(2y﹣1)][x+(2y﹣1)]
C. [(x﹣2y)+1][(x﹣2y)﹣1]
D. [(x+1)﹣2y][(x+1)+2y]
【方法总结】
平方差公式一般是两数的和与它们的差的积等于这两数的平方差,但这里边的a和b也可以
用式子来表示,对于(a-b+c)(a+b-c)这类题而言,我们可以对两个括号内的式子进行变形,目的是拼凑出两个数(或式子)的和与差的乘积形式,观察易得出(a-b+c)(a+b-c)=[a-(b-c)][a+(b-c)],这样就变成了a与(b-c)的和与差的乘积,所以可得出
(a-b+c)(a+b-c)=[a-(b-c)][a+(b-c)]=a2-(b-c)2然后再进行下一步计算.
【随堂练习】
1.(2018•包河区一模)计算:(x﹣3)2﹣(x﹣2)(x+2)
2.(2017秋•青浦区期末)计算(x+2)•(x﹣2)•(x2+4)
知识点2 利用平方差公式进行数的运算
在一些计算中,有时利用平方差公式,会使计算量大大减少;
例如98×102,可以利用平方差公式化成98×102=(100-2)×(100+2)=100²-2²=9996.【典例】
1.20132﹣2011×2015的计算结果是()
A. 2
B. ﹣2
C. 4
D. ﹣4
【方法总结】
此题主要考查了平方差公式,关键是掌握22
a b a b a b
+-=-
()()
本题直接计算,计算量很大,观察式子可以发现,题目中给出了20132,所以在对后面的式子进行变形时,尽量凑出2013,那么很容易得出2011=2013-2,2015=2013+2,再利用平方差公式2011×2015=(2013-2)×(2013+2),然后再计算即可.
【随堂练习】
1.(2018•萧山区二模)计算:(﹣2018)2+2017×(﹣2019).
2.(2018•滦南县二模)请你参考黑板中老师的讲解,用乘法公式进行简便计算:
(1)9992;
(2)20182﹣2017×2019.
知识点3 利用平方差公式进行整式的运算
【典例】
1.如果(m+1+n)(m-1+n)=8,那么m+n的值为()
A. ±9
B. ±3
C. 3
D. 9
【方法总结】
通过上边的学习我们知道,对于这种两个三项式相乘,我们可以对两个三项式变形,使他们分别变成两个数(或式子)的和与差相乘的形式,然后再利用平方差公式进行下一步计算,除此之外需要注意,结果是两个数,二者互为相反数.
【随堂练习】
1.(2017秋•黄浦区期中)计算:(2a﹣b+c)(2a﹣b﹣c).
2.(2017秋•凤庆县期末)计算:(x﹣2y+3)(x+2y﹣3)
3.(2018春•兴化市期中)计算:
(1)(2a+1)(﹣a﹣2);
(2)(x+y﹣3)(x﹣y+3).
知识点4 平方差公式—几何背景
平方差公式的证明方法有很多种,其中几何法证明是最常见的一种,也是初中阶段最容易理解的一种.
【典例】
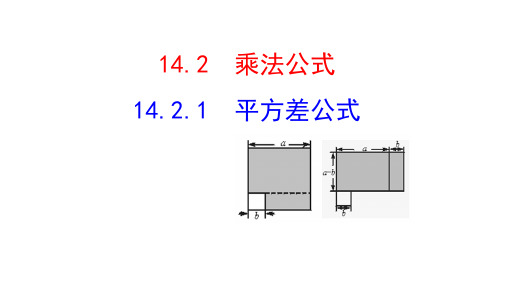
1.如图1,在边长为a的正方形中剪去一个边长为b的小正形(a>b),把剩下部分拼成一个梯形(如图2),利用这两幅图形面积,可以验证的公式是()
A. (a+b)(a﹣b)=a2+b2
B. (a+b)(a﹣b)=a2﹣b2
C. (a+b)2=a2+2ab+b2
D. (a﹣b)2=a2﹣2ab+b2
【方法总结】
本题考查了平方差公式的几何背景,认识不同表示方法之间的关系,解题的重要点是利用面积的不变性.
【随堂练习】
1.(2018春•常熟市期末)(1)如图1,阴影部分的面积是______.(写成平方差的形式)
(2)若将图1中的阴影部分剪下来,拼成如图2的长方形,面积是_____.(写成多项式相乘的积形式)
(3)比较两图的明影部分的面积,可以得到公式:_________.
(4)应用公式计算:(1﹣)(1﹣)(1﹣)(1﹣)…(1﹣)
(1﹣).
2.(2018春•怀远县期末)如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2中阴影部分剪裁后拼成的一个长方形.
(1)设如图1中阴影部分面积为S1,如图2中阴影部分面积为S2,请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1
3.(2018春•平和县期中)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为____,图2中阴影部分面积为_____,对照两个图形的面积可以验证____公式(填公式名称)请写出这个乘法公式_____.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.
综合运用
1.(x+2)(x﹣2)(x2+4)的计算结果是__________
2.若(x﹣ay)(x+ay)=x2﹣16y2,则a=.
3.(m+3)(m﹣3)=.
4.计算:(﹣m+n)(﹣m﹣n)=.
5.化简(a﹣1)(a+1)(a2+1)﹣(a4﹣1)的结果为___________
6.计算20072﹣2006×2008得_______
7.已知A=99×100×101,B=98×100×102,则A﹣B的值是___________
8.计算(2x﹣3y+1)(2x+3y﹣1)的结果是_________
9.如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是___________。