2018年秋九年级数学上册第2章对称图形_圆2.2圆的对称性第1课时圆的旋转不变性同步练习新版苏科版156
- 格式:doc
- 大小:695.00 KB
- 文档页数:7

2.2 圆的对称性第2课时圆的轴对称性与垂径定理知|识|目|标1.通过回顾轴对称图形的概念,了解圆是轴对称图形.2.通过探索圆的轴对称性,掌握并应用垂径定理求线段的长度.3.通过对实际问题的分析,能用垂径定理解决实际问题.目标一了解圆的轴对称性例1 教材补充例题圆是轴对称图形,它的对称轴有( )A.1条 B.2条 C.4条 D.无数条【归纳总结】圆的轴对称性:(1)圆的对称轴是经过圆心的每一条直线,而直径不是圆的对称轴,直径所在的直线才是圆的对称轴.(2)轴对称图形的对应边相等,对应角相等.目标二会利用垂径定理进行计算例2 教材补充例题如图2-2-5,AB为⊙O的弦,AB=8,OC⊥AB于点D,交⊙O于点C,且CD=1,求⊙O的半径.图2-2-5例3 教材例2变式如图2-2-6,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.若AB=10 cm,CD=6 cm,求AC的长.图2-2-6【归纳总结】应用垂径定理的关键点:利用垂径定理进行计算,通常是在半径、圆心到弦的垂线段和弦长的一半所构成的直角三角形中,利用勾股定理求出未知线段的长.目标三 能利用垂径定理解决实际问题例 4 教材补充例题我国隋朝建造的赵州石拱桥(示意图如图2-2-7)的主桥拱是圆弧形,它的跨度AB (弧所对的弦的长)为37 m ,拱高(弧的中点到弦的距离,也叫弓形高)为7.23 m ,求主桥拱的半径(结果精确到0.1 m).图2-2-7【归纳总结】利用垂径定理构造直角三角形是解决此类问题的关键,有时还引入方程求解,可达到事半功倍的效果.知识点一 圆的轴对称性圆是轴对称图形,过______的任意一条直线都是它的对称轴. [点拨] (1)圆既是轴对称图形,也是中心对称图形; (2)圆有无数条对称轴. 知识点二 垂径定理垂直于弦的______平分弦以及弦所对的两条________. [点拨]图2-2-8如图2-2-8.(1)垂径定理的几何语言表示:⎭⎪⎬⎪⎫CD 是⊙O 的直径,CD ⊥AB 于点E⇒⎩⎪⎨⎪⎧AE =BE ,AC ︵=BC ︵,AD ︵=BD ︵.(2)垂径定理的补充说明:在①CD 是⊙O 的直径;②CD ⊥AB ;③AE =BE ;④AC ︵=BC ︵;⑤AD ︵=BD ︵这五个条件中,只要具备其中的两个,其他三个结论都正确.已知CD 是⊙O 的一条弦,作直径AB ,使AB ⊥CD ,垂足为E .若AB =10,CD =8,求BE 的长.图2-2-9解:如图2-2-9,连接OC ,则OC =5. ∵AB 是⊙O 的直径,AB ⊥CD , ∴CE =12CD =4.在Rt △OCE 中,OE =OC 2-CE 2=3,∴BE =OB +OE =5+3=8.以上解答过程完整吗?若不完整,请进行补充.详解详析【目标突破】例1 [解析] D 圆是轴对称图形,经过圆心的每一条直线都是它的对称轴. 例2解:如图,连接OA.由OC⊥AB 于点D ,得AD =DB =12AB =4.设⊙O 的半径为r ,在Rt △OAD 中,OA 2=AD 2+OD 2,即r 2=42+(r -1)2, 整理,得2r =17, ∴r =172.故⊙O 的半径是172.例3 [解析] 根据题意,过点O 作OE⊥AB 于点E ,根据垂径定理可以求出AE ,CE 的长度,这样AC 的长度也就不难求出了.解:如图,过点O 作OE⊥AB 于点E.根据垂径定理,可知AE =12AB =5 cm ,CE =12CD =3 cm ,∴AC =AE -CE =2 cm .例4 解:如图所示,设AB ︵所在圆的圆心为O ,半径为R m ,经过圆心O 作弦AB 的垂线OD ,D 为垂足,与AB ︵相交于点C.由题知AB =37,CD =7.23, ∴AD =12AB =12×37=18.5,OD =OC -CD =R -7.23.在Rt △OAD 中,由勾股定理,得OA 2=AD 2+OD 2,即R 2=18.52+(R -7.23)2.解得R≈27.3.答:赵州石拱桥的主桥拱半径约为27.3 m .备选目标一 利用弦、圆心角、弧的关系求最值例1 如图,MN 为⊙O 的直径,A ,B 是⊙O 上的两点,过点A 作AC⊥MN 于点C ,过点B 作BD⊥MN 于点D ,P 是直径MN 上的任意一点.若MN =20,AC =8,BD =6,则PA +PB 的最小值是________.[答案] 14 2[解析] 利用轴对称性,确定点B 关于MN 的对称点,再利用勾股定理求解即可.如图所示,延长BD 交⊙O 于点B′,连接B′A,则B ′A 的长度为所求的最小值.过点B′向AC 的延长线作垂线,垂足为E ,连接AO ,BO ,则AO =BO =12MN =10,所以OD =BO 2-BD 2=8,OC=AO 2-AC 2=6.在Rt △AB ′E 中,AE =8+6=14,B ′E =8+6=14,所以AB′=AE 2+B′E 2=14 2,即PA +PB 的最小值是14 2.[归纳总结] 解决这类问题先要明确哪个点是定点,哪个点是动点,动点在何处运动,找到符合模型的图形元素后,再运用轴对称的方法将问题转化为“两点之间,线段最短”的问题.备选目标二 实际应用例2 如图,某地有一座弧形的拱桥,桥下的水面宽度为7.2米,拱顶高出水面2.4米,现有一艘宽3米,船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?[解析] 判断货船能否通过这座拱桥,关键是看船舱顶部两角是否会被拱桥顶部挡住.如图所示,实际问题就转化为求FN 的长度.解:如图,设圆心为O ,连接OA ,ON ,过点O 作OD⊥AB 于点D ,交⊙O 于点C ,交MN 于点H.由垂径定理可知,D 为AB 的中点.设OA =r 米,则OD =OC -DC =(r -2.4)米,AD =12AB=3.6米.在Rt△AOD中,OA2=AD2+OD2,即r2=3.62+(r-2.4)2,解得r=3.9.在Rt△OHN中,OH=ON2-NH2= 3.92-1.52=3.6(米).所以FN=DH=OH-OD=3.6-(3.9-2.4)=2.1(米).因为2.1米>2米,所以货船可以顺利通过这座拱桥.[归纳总结] 垂径定理为证明线段相等、角相等、垂直关系及利用勾股定理计算有关线段的长提供了依据.垂径定理的三要素:垂直、平分、过圆心(直径),它们在圆内常常构成相等的角、线段、直角三角形等,从而可利用勾股定理或解直角三角形的方法进行有关证明或计算.【总结反思】[小结] 知识点一圆心知识点二直径弧[反思]不完整.补充如下:如图,当垂足E在线段OB上时,此时BE=OB-OE=5-3=2.∴BE的长为8或2.。
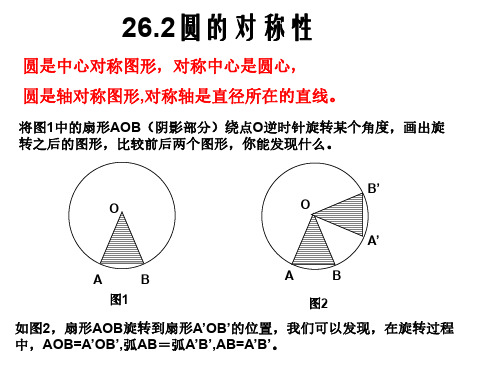


九年级数学圆的对称性知识点圆是数学中一个非常重要的几何概念,它具有丰富的对称性质。
在九年级数学中,我们学习了许多有关圆对称性的知识点。
本文将围绕这一主题,探讨圆的对称性在数学中的应用和意义。
1. 点、线和面的对称性在数学中,几何图形可以根据其对称性质进行分类。
点对称性是最基本的对称性质,它是指图形绕着一个固定点旋转180度后能够重合。
线对称性是指图形相对于一条线对称,两侧对应部分完全一致。
面对称性则是指图形相对于一个面对称,两侧对应部分完全一致。
对称性在几何学中具有重要的应用,它能够帮助我们分析和解决许多问题。
2. 圆的旋转对称性圆具有旋转对称性,这是因为任何一个圆可以绕着其圆心旋转一定角度后得到一个与原圆完全一致的新圆。
这个旋转角度称为圆的旋转角,它可以是任意角度。
利用圆的旋转对称性,我们可以解决许多有关圆的问题,比如确定两个圆是否相等、快速计算圆的周长和面积等。
3. 圆的轴对称性除了旋转对称性,圆还具有轴对称性。
轴对称性是指圆相对于一条直线对称,即对于圆上的任意一点P,当P的关于直线L的对称点也在圆上时,称直线L为圆的轴线。
利用圆的轴对称性,我们可以判断一个图形是否关于某条直线对称,从而简化几何证明的过程。
4. 圆的纵轴对称性和横轴对称性圆的轴对称性可以进一步分为纵轴对称性和横轴对称性。
当圆相对于一条垂直于x轴的直线对称时,称这条直线为圆的纵轴线;当圆相对于一条垂直于y轴的直线对称时,称这条直线为圆的横轴线。
纵轴对称性和横轴对称性在解决一些几何问题时非常有用,可以帮助我们找到图形的对称性质,简化问题的分析。
5. 圆的切线与辅助线的对称性在与圆相关的问题中,切线和辅助线的对称性也是常见且有用的。
以圆的切线为例,对于圆上的任意一点P,过点P作一条切线,这条切线与半径的夹角为90度,且在切点处与圆相切。
利用切线的对称性,我们可以解决一些与圆的切线有关的几何问题,比如判断切线与圆的位置关系、计算切线的长度等。


第2章 对称图形——圆
2.2 第1课时 圆的旋转不变性
知识点 1 圆的旋转不变性 1.一个圆绕圆心旋转任何角度后,都能与________重合.圆是中心对称图形,它的对称中心是________.
知识点 2 弧、弦、圆心角的关系
2.如图2-2-1,在⊙O 中,AB ︵=AC ︵
,∠AOB =122°,则∠AOC 的度数为( ) A .122° B .120° C .61° D .58° 3.下列结论中,正确的是( )
A .同一条弦所对的两条弧一定是等弧
B .等弧所对的圆心角相等
C .相等的圆心角所对的弧相等
D .长度相等的两条弧是等弧
图2-2-1
图2-2-2
4.如图2-2-2,在⊙O 中,若C 是AB ︵
的中点,∠A =50°,则∠BOC 等于( ) A .40° B .45° C .50° D .60°
5.如图2-2-3,已知BD 是⊙O 的直径,点A ,C 在⊙O 上,AB ︵=BC ︵
,∠AOB =60°,则∠COD 的度数是________.
图2-2-3
图2-2-4
6.教材练习第1题变式如图2-2-4,AB 是⊙O 的直径,BC ︵=CD ︵=DE ︵
,∠BOC =40°,则∠AOE =________°.
7.在⊙O 中,若弦AB 的长恰好等于半径,则弦AB 所对的圆心角的度数为________.
8.教材习题2.2第4题变式如图2-2-5,在⊙O 中,AB ,CD 是两条直径,弦CE ∥AB ,EC ︵
的度数是40°,求∠BOD 的度数.
图2-2-5
9. 已知:如图2-2-6,点A ,B ,C ,D 在⊙O 上,AB =CD .求证:∠AOC =∠DOB .
图2-2-6
10.如图2-2-7,在⊙O 中,CD 为⊙O 的直径,AC ︵=BC ︵
,E 为OD 上任意一点(不与点O ,D 重合).求证:AE =BE .
图2-2-7
11.在同圆中,若AB ︵和CD ︵都是劣弧,且AB ︵=2CD ︵
,则弦AB 和弦CD 的大小关系是( ) A .AB =2CD B .AB >2CD C .AB <2CD
D .无法比较它们的大小
12.[2016秋·无锡校级月考] 如图2-2-8,已知AB 是⊙O 的直径,M,N 分别是AO,BO 的中点,过点M,N 分别作CM⊥AB ,DN ⊥AB.
求证:AC ︵=BD ︵
.
图2-2-8
13.如图2-2-9,在△ABO 中,∠A =∠B ,⊙O 与OA 交于点C,与OB 交于点D,与AB 交于点E,F.
(1)求证:CE ︵=DF ︵
;
(2)写出图中所有相等的线段(不要求证明).
图2-2-9
14.如图2-2-10,PA ︵=PB ︵
,C,D 分别是半径OA,OB 的中点,连接PC,PD 交弦AB 于E,F 两点.
求证:(1)PC =PD ; (2)PE =PF.
图2-2-10
15.如图2-2-11所示,在⊙O 中,AB,CD 是两条弦,OE ⊥AB,OF ⊥CD,垂足分别为E,F. (1)如果∠AOB=∠COD ,那么OE 与OF 的大小有什么关系?为什么?
(2)如果OE =OF,那么AB 与CD 的大小有什么关系?AB ︵与CD ︵
的大小有什么关系?为什么?∠AOB 与∠COD 呢?
图2-2-11
1.自身 圆心 2.A
3.B [解析] A .同一条弦所对的两条弧不一定是等弧,有可能是一条优弧和一条劣弧,故本选项错误;B .正确;C .在两个同心圆中,同一个圆心角所对的弧不相等,故本选项错误;D .长度相等的两条弧,弯曲程度不同,就不能重合,就不是等弧,故本选项错误.故选B .
4.A [解析] ∵∠A=50°,OA =OB,∴∠B =∠A=50°,∴∠AOB =180°-50°-50°=80°.∵C 是AB ︵的中点,∴∠BOC =1
2
∠AOB=40°.故选A .
5.120° [解析] ∵AB ︵=BC ︵
,∠AOB =60°,∴∠BOC =∠AOB =60°.∵BD 是⊙O 的直径,∴∠BOD =180°,∴∠COD =180°-∠BOC=120°.
6.60 [解析] 由BC ︵=CD ︵=DE ︵
,可得∠BOC=∠COD =∠DOE=40°,所以∠AOE=180°-3×40°=60°.
7.60°
8.解:如图,连接OE.∵EC ︵
的度数是40°,
∴∠EOC =40°.
∵OE =OC,∴∠C =70°. ∵CE∥AB ,
∴∠BOC =∠C=70°, ∴∠BOD =110°. 9.证明:∵AB=CD, ∴AB ︵=CD ︵,
∴∠AOB =∠COD ,
∴∠AOB -∠BOC=∠COD-∠BOC , 即∠AOC=∠DOB. 10.证明:∵AC ︵=BC ︵
,
∴∠AOC =∠BOC ,∴∠AOE =∠BOE. ∵OA,OB 是⊙O 的半径,∴OA =OB.
在△AOE 和△BOE 中,∵OA =OB,∠AOE =∠BOE ,OE =OE, ∴△AOE ≌△BOE,∴AE =BE.
11.C [解析] 如图,取AB ︵的中点E,连接AE,BE,∴AB ︵=2AE ︵=2BE ︵
, ∴AE =BE. ∵AB ︵=2CD ︵,
∴AE ︵=BE ︵=CD ︵, ∴AE =BE =CD, ∴AE +BE =2CD. ∵AE +BE >AB, ∴2CD >AB. 故选C .
12.证明:连接OC,OD,如图.
∵AB 是⊙O 的直径,M,N 分别是AO,BO 的中点, ∴OM =ON.
∵CM ⊥AB ,DN ⊥AB,
∴∠OMC =∠OND=90°.
在Rt △OMC 和Rt △OND 中,⎩
⎪⎨⎪⎧OM =ON ,
OC =OD ,
∴Rt △OMC ≌Rt △OND,
∴∠COM =∠DON , ∴AC ︵=BD ︵.
13.解:(1)证明:连接OE,OF,则OE =OF,∴∠OEF =∠OFE. ∵∠A =∠B ,∴∠AOE=∠BOF ,∴CE ︵=DF ︵
. (2)OA =OB,OC =OD,AC =BD,AE =BF,AF =BE. 14.证明:(1)连接PO. ∵PA ︵=PB ︵
,∴∠POC =∠POD. ∵C,D 分别是半径OA,OB 的中点, ∴OC =OD. 又∵PO=PO, ∴△PCO ≌△PDO, ∴PC =PD.
(2)∵△PCO≌△PDO , ∴∠PCO =∠PDO.
∵OA =OB,∴∠A =∠B ,
∴∠AEC =∠BFD , ∴∠PEF =∠PFE , ∴PE =PF.
15.解:(1)OE =OF.理由如下: ∵OA =OC,∠AOB =∠COD ,OB =OD, ∴△AOB ≌△COD(SAS ). ∵OE ⊥AB,OF ⊥CD,AB =CD,
∴OE =OF(全等三角形对应边上的高相等). (2)AB =CD,AB ︵=CD ︵
,∠AOB =∠C OD. 理由如下:∵OE⊥AB ,OF ⊥CD, ∴∠AEO =∠CFO=90°. 在Rt △AOE 和Rt △COF 中, ∵OE =OF,OA =OC,
∴Rt △AOE ≌Rt △COF(HL ), ∴AE =CF. 同理BE =DF, ∴AB =CD,
∴AB ︵=CD ︵
,∠AOB =∠COD.。