4.5H法验算路基稳定性

路基边坡稳定性分析本设计计算内容为广西梧州绕城高速公路东段k15+400～k16+800路段中出现的最大填方路段。

该路堤边坡高22m，路基宽26m，需要进行边坡稳定性验算。

1.确定本设计计算的基本参数本段路段路堤边坡的土为粘性土，根据《公路路基设计规范》，取土的容重γ=18.5kN/m³，粘聚力C=20kpa，内摩擦角C=24º，填土的内摩擦系数ƒ=tan24º=0.445。

2.行车荷载当量高度换算高度为:25500.8446(m)5.512.818.5NQhBLλ⨯===⨯⨯h0—行车荷载换算高度；L—前后轮最大轴距，按《公路工程技术标准》（JTG B01-2003）规定对于标准车辆荷载为12.8m；Q—一辆车的重力（标准车辆荷载为550kN）；N—并列车辆数，双车道N=2，单车道N=1；γ—路基填料的重度（kN/m3）；B—荷载横向分布宽度，表示如下：(N1)m dB Nb=+-+式中：b—后轮轮距，取1.8m；m—相邻两辆车后轮的中心间距，取1.3m；d—轮胎着地宽度，取0.6m。

3. Bishop法求稳定系数K3.1 计算步骤：（1）按4.5H 法确定滑动圆心辅助线。

由表查得β1=26°，β2 =35°及荷载换算为土柱高度h0 =0.8446(m),得G点。

a .由坡脚A 向下引竖线，在竖线上截取高度H=h+h0（h 为边坡高度，h0 为换算土层高）b.自G 点向右引水平线，在水平线上截取4.5H，得E 点。

根据两角分别自坡角和左点作直线相交于F 点，EF 的延长线即为滑动圆心辅助线。

c.连接边坡坡脚A 和顶点B ，求得AB 的斜度i=1/1.5，据此查《路基路面工程》表4-1得β1,β2。

图1(4.5H 法确定圆心)（2）在CAD 上绘出五条不同的位置的滑动曲线 （3）将圆弧范围土体分成若干段。

（4）利用CAD 功能读取滑动曲线每一分段中点与圆心竖曲线之间的偏角αi (圆心竖曲线左侧为负，右侧为正)以及每分段的面积S i 和弧长L i ； （5）计算稳定系数：首先假定两个条件：a,忽略土条间的竖向剪切力X i 及X i+1 作用；b,对滑动面上的切向力T i 的大小做了规定。

第四章路基稳定性分析计算（路基工程）路基工程第四章路基稳定性分析计算4.1边坡稳定性分析原理4.2直线滑动面的边坡稳定性分析4.3曲线滑动面的边坡稳定性分析4.4软土地基的路基稳定性分析4.5浸水路堤的稳定性分析4.6路基边坡抗震稳定性分析一、边坡稳定原理：力学计算基本方法是分析失稳滑动体沿滑动面上的下滑力T与抗滑力R，按静力平衡原理，取两者之比值为稳定系数K，即K=R T1、假设空间问题—>平面问题（1）通常按平面问题来处理（2）松散的砂性土和砾（石）土在边坡稳定分析时可采用直线破裂法。

（3）粘性土在边坡稳定分析时可采用圆弧破裂面法。

一、边坡稳定原理：一般情况下，对于边坡不高的路基（不超过8.0的土质边坡，不超过12.0m的石质边坡），可按一般路基设计，采用规定的边坡值，不做稳定性分析；地质与水文条件复杂，高填深挖或特殊需要的路基，应进行边坡稳定性分析计算，据此选定合理的边坡及相应的工程技术。

一、边坡稳定原理：边坡稳定分析时，大多采用近似的方法，并假设：（1）不考虑滑动土体本身内应力的分布。

（2）认为平衡状态只在滑动面上达到，滑动土体整体下滑。

（3）极限滑动面位置需要通过试算来确定。

二、边坡稳定性分析的计算参数：（一）土的计算参数：1、对于路堑或天然边坡取：原状土的容重γ，内摩擦角和粘聚力2、对于路堤边坡，应取与现场压实度一致的压实土的试验数据3、边坡由多层土体所构成时（取平均值）c = i=1n c i ?ii=1n ?itanφ= i=1n ?i tgφii=1n ?iγ= i=1n γi ?ii=1n ?i第一节边坡稳定性分析原理二、边坡稳定性分析的计算参数：（二）边坡稳定性分析边坡的取值：对于折线形、阶梯形边坡：取平均值。

（三）汽车荷载当量换算：边坡稳定分析时，需要将车辆按最不利情况排列，并将车辆的设计荷载换算成当量土柱高，以?0表示：0=NQγBL式中：N—横向分布的车辆数（为车道数）；Q—每辆重车的重力，kN （标准车辆荷载为550kN）；L—汽车前后轴的总距；B—横向分布车辆轮胎最外缘之间的距离；B=Nb+（N-1）m+d式中：b—后轮轮距，取1.8m；m—相邻两辆车后轮的中心间距，取1.3m；d—轮胎着地宽度，取0.6m；三、边坡稳定性分析方法：一般情况，土质边坡的设计，先按力学分析法进行验算，再以工程地质法予以校核，岩石或碎石土类边坡则主要采用工程地质法，有条件时可以力学分析进行校核。

路基边坡稳定性验算路基土为粘性土质，拟定基本参数为：土的粘聚力kpac 10=，内摩擦角25º，容重3/16mkN =γ。

荷载按黄河JN-150。

取全线未设挡土墙处最高路堤处行边坡稳定性验算，桩号为K1+020。

粘性土质采用圆弧破裂面法，并用条分发进行土坡稳定性分析。

（1）将黄河JN-150换算成土柱高。

按最不利的情况其中一辆黄河车停在路肩上，另一辆以最小间距md4.0=与它并排按下式换算土柱高BLNQh γ=式中：N ----横向分布车辆数，单车道1=N ，双车道2=N ；Q----每一辆车的重量，KN ； L ----汽车前后轴的总距，m;B----横向分布车辆轮胎最外缘之间总距，m ；()dN Nb B 1-+=其中：b ----每一辆车轮胎最外缘之间的距离，m ；d----相邻两辆车轮胎之间的距离，m考虑到车辆停放在路肩上，认为0h 厚的当量土层分布在整个路基宽度上。

∴ ()md N Nb B4.74.05.321=+⨯=-+=∴ mBLNQh 570.02.44.7176.15020=⨯⨯⨯==γ（2）采用4.5H 法确定圆心辅助线，具体如下： ①由坡脚E 向下引竖线，在竖线上截取高度mh h H 77.7570.02.70=+=+=得F 点。

②自F 向右引水平线，在水平线上截取mH965.3477.75.45.4=⨯=，得M 点。

③连接边坡坡脚E 和顶点S ，求得SE 的斜度39.1:172.10:759.70==i ，据此查粘土边坡表得35,2621==ββ。

由E 点作与SE 成1β角的直线，再由S 点作与水平线成2β角的直线，两条直线交于点I 。

④连接I 和M 两点得到圆心辅助线。

（3）绘出三条不同位置的滑动曲线（都过坡脚）：①一条过路基中线；②一条过路基边缘；③一条过距左边缘1/4路基宽度处。

（4）通过平面几何关系找出三条滑动曲线各自的圆心。

（5）将土基分段，每段如图（图中以曲线①和曲线②为例进行划分，段始于左侧）宽1m ，最后一段可能略小一点。

路基边坡稳定性验算计算书
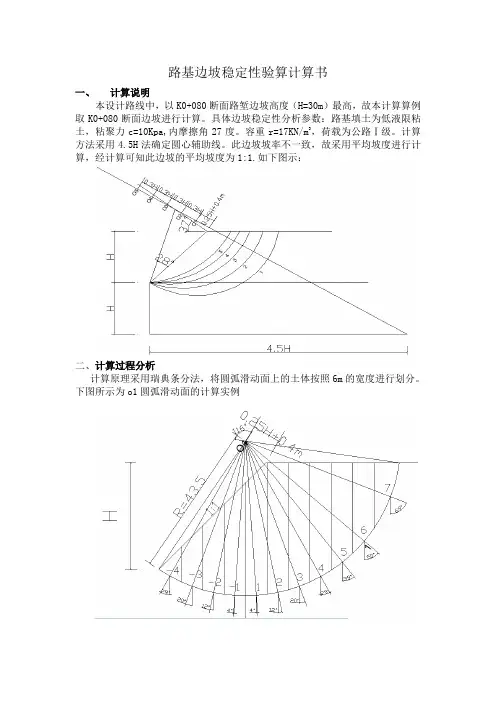
一、计算说明
本设计路线中，以K0+080断面路堑边坡高度（H=30m）最高，故本计算算例取K0+080断面边坡进行计算。

具体边坡稳定性分析参数：路基填土为低液限粘土，粘聚力c=10Kpa,内摩擦角27度。

容重r=17KN/m3，荷载为公路Ⅰ级。

计算方法采用4.5H法确定圆心辅助线。

此边坡坡率不一致，故采用平均坡度进行计算，经计算可知此边坡的平均坡度为1:1.如下图示：
二、计算过程分析
计算原理采用瑞典条分法，将圆弧滑动面上的土体按照6m的宽度进行划分。

下图所示为o1圆弧滑动面的计算实例
采用计算表格可得计算结果：
L=
=R θπ
180
88.02m 则边坡稳定系数为： =
+=
∑∑i
hi b i
hi b cL Ks θγθϕγsin cos tan =⨯⨯⨯⨯⨯+⨯505
.9661701
.23927tan 61702.8810 1.35>1.25
按照上述方法一一计算出o2、o3、o4、o5处的稳定系数分别为1.32、1.29、1.33、1.37.故取Ks=1.29为最小的稳定系数，此时由于Ks>1.25,所以边坡稳定性满足要求。

第二节边坡稳定性分析方法力学验算法和工程地质法是路基边坡稳定性分析和验算方法常用的两种方法。

1．力学验算法(1)数解法假定几个不同的滑动面，按力学平衡原理对每个滑动面进行验算，从中找出最危险滑动面，按此最危险滑动面的稳定程度来判断边坡的稳定性。

此方法计算较精确，但计算繁琐。

(2)图解或表解法在图解和计算的基础上，经过分析研究，制定图表，供边坡稳定性验算时采用。

以简化计算工作。

2．工程地质法根据稳定的自然山坡或已有的人工边坡进行土类及其状态的分析研究，通过工程地质条件相对比，拟定出与路基边坡条件相类似的稳定值的参考数据，作为确定路基边坡值的依据。

一般土质边坡的设计常用力学验算法进行验算，用工程地质法进行校核；岩石或碎石土类边坡则主要采用工程地质法进行设计。

3．力学验算法的基本假定滑动土楔体是均质各向同性、滑动面通过坡脚、不考虑滑动土体内部的应力分布及各土条(指条分法)之间相互作用力的影响。

一、直线滑动面法松散的砂类土路基边坡，渗水性强，粘性差，边坡稳定主要靠其内摩擦力。

失稳土体的滑动面近似直线状态，故直线滑动面法适用于砂类土：如图2-2-4所示，验算时，先通过坡脚或变坡点假设一直线滑动面，将路提斜上方分割出下滑土楔体ABD，沿假设的滑动面AD滑动，其稳定系数K按下式计算(按边坡纵向单位长度计)：验算的边坡是否稳定，取决于最小稳定系数Kmin的值。

当Kmin＝1.0时，边坡处于极限平衡状态。

由于计算的假定，计算参数(r，Ψ，c)的取值都与实际情况存在一定的差异，为了保证边坡有足够的稳定性，通常以最小稳定系数Kmin≥1.25来判别边坡的稳定性。

但Kmin过大，则设计偏于保守，在工程上不经济。

当路堤填料为纯净的粗砂、中砂、砾石、碎石时，其粘聚力很小，可忽略不计，则式（2-2-3）变为：式(2-2-3)也适用于均质砂类土路堑边坡的稳定性验算。

二、圆弧滑动面法用粘性土填筑的路堤，边坡滑坍时的破裂面形状为一曲面，为简化计算，通常近似地假设为一圆弧状滑动面。

路基边坡稳定性设计路基边坡滑坍是公路上常见的破坏现象之一。

例如，在岩质或土质山坡上开挖路堑，有可能因自然平衡条件被破坏或边坡过陡，使坡体沿某一滑动面产生滑动。

对河滩路堤、高路堤或软弱地基上的路堤，也可能因水流冲刷、边坡过陡或地基承载力过低而出现填方土体（或连同原地面土体）沿某一剪切面产生坍塌。

路基边坡的稳定性涉及岩土性质与结构、边坡高度与坡度、工程质量与经济等因素。

一般情况下，对边坡不高的路基，如不超过8 m的土质边坡、不超过12 m 的石质边坡，可按一般路基设计，采用规定的坡度值，不作稳定性分析计算。

对地质和水文条件复杂、高填深挖或有特殊使用要求的路基，应进行稳定性分析，保证路基设计既满足稳定性要求，又满足经济性要求。

4.1 边坡稳定性分析概述4.1.1 影响路基边坡稳定性的因素根据土力学原理，路基边坡滑坍是因边坡土体中的剪应力超过其抗剪强度所产生的剪切破坏。

因此，凡是使土体剪应力增加或抗剪强度降低的因素，都可能引起边坡滑坍。

这些因素可归纳为以下5点：①边坡土质。

土的抗剪强度取决于土的性质，土质不同则抗剪强度也不同。

对于路堑边坡而言，除与土或岩石的性质有关外，还与岩石的风化破碎程度和形状有关。

②水的活动。

水是影响边坡稳定性的主要因素，边坡的破坏总是或多或少地与水的活动有关。

土体的含水率增加，既降低了土体的抗剪强度，又增加了土内的剪应力。

在浸水情况下，还有浮力和动水压力的作用，使边坡处于最不利状态。

③边坡的几何形状。

边坡的高度、坡度等直接关系土的稳定条件，高大、陡直的边坡，因重心高，稳定条件差，易发生滑坍或其他形式的破坏。

④活荷载增加。

坡脚因水流冲刷或其他不适当的开挖而使边坡失去支承等，均可能增大边坡土体的剪应力。

⑤地震及其他震动荷载。

4.1.2 边坡稳定性分析方法路基边坡稳定性分析与验算的方法很多，归纳起来有力学分析法、图解法和工程地质法（比拟法）。

力学分析法又称极限平衡法，假定边坡沿某一形状滑动面破坏，按力学平衡原理进行计算。

O
R
βi
B d
c
A i Wi Ti Ni
i ab
i i
4.滑动面的总滑动力矩
C
T R R T iR W isiin
5.滑动面的总抗滑力矩
H
T R R fliiR itain cili
R (W icoitsain cili)

6.确定安全系数
KT TR RW i co W sisitig n iicili
第四章 路基稳定性 设计
第一节 概述
1、边坡失稳现象 路基边坡滑坍是公路上常见的破坏现象之一。在
岩质或土质山坡上开挖路堑，有可能因自然平衡条件 被破坏或者因边坡过陡，使坡体沿某一滑动面产生滑 坡。对河滩路堤、高路堤或软弱地基上的路堤，因水 流冲刷、边坡过陡或地基承载力过低而出现填方土体 （或连同原地面土体）沿某一剪切面产生坍塌。
2、圆弧滑动面的图式
重点：圆弧圆心确定
为了较快地找到极限滑动面，减少试算工作量，根据经验， 极限滑动圆心在一条线上，该线即是圆心辅助线。确定圆心辅 助线可以采用4.5 H法或36°线法。
4.5H法：过E向下作垂直
EF=H，过F作水平线FM=4.5H， 过E作一线EI与ES夹β1角，过S 作IS与水平线夹角β2，交于I点， 连IM作延长线，在其上取O1、 O2、O3点，求K1、K2、K3，取 小值。
例：路堤高12m，顶宽16m，土的c＝10KPa，f=0.404,r＝ 16.8KN/m3边坡坡度1：1.5，用表解法分析K.
第四节 软土地基稳定性分析
软土是由天然含水率大、压缩性高、承载能力低的淤泥沉积物 及少量腐殖质所组成的土，主要有淤泥、淤泥质土及泥炭。
软土分为四种：河海沉积、湖泊沉积、江滩沉积、沼泽沉积

路基工程第四章路基稳定性分析计算4.1边坡稳定性分析原理4.2直线滑动面的边坡稳定性分析4.3曲线滑动面的边坡稳定性分析4.4软土地基的路基稳定性分析4.5浸水路堤的稳定性分析4.6路基边坡抗震稳定性分析一、边坡稳定原理：力学计算基本方法是分析失稳滑动体沿滑动面上的下滑力T与抗滑力R，按静力平衡原理，取两者之比值为稳定系数K，即K=RT1、假设空间问题—>平面问题（1）通常按平面问题来处理（2）松散的砂性土和砾（石）土在边坡稳定分析时可采用直线破裂法。

（3）粘性土在边坡稳定分析时可采用圆弧破裂面法。

一、边坡稳定原理：⏹一般情况下，对于边坡不高的路基（不超过8.0的土质边坡，不超过12.0m的石质边坡），可按一般路基设计，采用规定的边坡值，不做稳定性分析；⏹地质与水文条件复杂，高填深挖或特殊需要的路基，应进行边坡稳定性分析计算，据此选定合理的边坡及相应的工程技术。

一、边坡稳定原理：边坡稳定分析时，大多采用近似的方法，并假设：（1）不考虑滑动土体本身内应力的分布。

（2）认为平衡状态只在滑动面上达到，滑动土体整体下滑。

（3）极限滑动面位置需要通过试算来确定。

二、边坡稳定性分析的计算参数：（一）土的计算参数：1、对于路堑或天然边坡取：原状土的容重γ，内摩擦角和粘聚力2、对于路堤边坡，应取与现场压实度一致的压实土的试验数据3、边坡由多层土体所构成时（取平均值）c = i=1n c i ℎii=1n ℎitanφ= i=1n ℎi tgφii=1n ℎiγ= i=1n γi ℎii=1n ℎi第一节边坡稳定性分析原理二、边坡稳定性分析的计算参数：（二）边坡稳定性分析边坡的取值：对于折线形、阶梯形边坡：取平均值。

（三）汽车荷载当量换算：边坡稳定分析时，需要将车辆按最不利情况排列，并将车辆的设计荷载换算成当量土柱高，以ℎ0表示：ℎ0=NQγBL式中：N—横向分布的车辆数（为车道数）；Q—每辆重车的重力，kN（标准车辆荷载为550kN）；L—汽车前后轴的总距；B—横向分布车辆轮胎最外缘之间的距离；B=Nb+（N-1）m+d式中：b—后轮轮距，取1.8m；m—相邻两辆车后轮的中心间距，取1.3m；d—轮胎着地宽度，取0.6m；三、边坡稳定性分析方法：一般情况，土质边坡的设计，先按力学分析法进行验算，再以工程地质法予以校核，岩石或碎石土类边坡则主要采用工程地质法，有条件时可以力学分析进行校核。

2边坡稳定性设计2.1 初始条件：路线经过区域路基填土为粘土，边坡为梯形边坡，分两级，土力学的指标：塑限14%，液限27%，含水量19%，天然容重18KN/m3，粘聚力19KPa，内摩擦角28°，公路按一级公路标准，双向四车道，设计车速为80Km/h，路基宽度为24.5m，荷载为车辆重力标准值550KN，中间护坡道取2m，车道宽度3.75m，硬路肩2.5m，土路肩0.75m，进行最不利布载时对左右各布3辆车。

H1=7m，H2=8m，I1=1:1.25，I2=1:1.52.2汽车荷载当量换算按荷载最不利布置条件，取单位长度路段，将车辆荷载换算成相当于路基沿途层厚度，以h0表示，计入滑动体的重力总去。

NQh0=γBL式中：ho—行车荷载转换高度L—前后轮最大轴距，对于标准车辆荷载为12.8m。

N—并列车辆数，取6。

Q—辆车的重量（标准车辆荷载为550KN）。

γ—路基填料的重度（KN/m3）。

B —荷载横向分布宽度，表示如下：B=Nb+(N －1)m+d式中： b —后轮轮距，取1.8m 。

M —相邻两辆车后轮的中心间距，取1.3m 。

D —轮胎着地宽度，取0.6m 。

计算：B=6×1.8+5×1.3+0.6=17.9mh 0=18×12.8×17.9550×6=0.8m计算高度：H =h 0+H 1+H 2=15.8m2.3 圆弧滑动面条分法分析2.3.1 按4.5H 线法确定圆心位置。

平均坡度I =(0.8+7+8)：(8.75+2+12)=1:1.44 查表4-1得β1=26°，,β2=35°∑∑+•=i i T cL N f k式中i N ------各土条的法向分力，i αcos i i Q N =。

i T ------各土条的切向分力有正负之分，i αsin i i Q T =。

i α------各土条的重心与圆心连线对竖轴y 的夹角，用CAD 确定。

编辑课件
rH
。。。。。。
例4-2：某挖方边坡，已知 =25°，C=14.7Kpa， γ=17.64KN/m3,H=6.0m。现拟采用1：0.5的边坡，试验算其 稳定性。 解：由Ctgθ= 0.5, θ=63°26’,Cscθ=1.1181
f= tg =tg25°=0.4663
a=2c/（γH）=2×14.7/(17.64×6.0)=0.2778
如何较快找到极限滑动面呢？ 根据经验，极限滑动圆心在一条直线上，该线即是
圆心辅助线。 确定圆心辅助线的方法： 4.5H法和36o度法。
编辑课件
(1)4.5H法(一)
①由坡脚E向下引竖线，在竖线上截取高度H=h+h0(边坡高度及荷载换算为土柱 高度h0)得F点。
②自F点向右引水平线，在水平线上截取4.5H，得M点。 ③连结边坡坡脚E和顶点S，求得SE的斜度i0＝1/m，据此值查表4-1得β1和β2值 。由E点作与SE成β1角的直线，再由S点作与水平线成β2角的直线，两线相交得I 点。④连结I和M两点即得圆心辅助线
编辑课件
3、所需参数取值 1）对于路堑或天然土坡为： ① 原状土容重γ（kN/m3） ② 内摩擦角φ（°） ③ 粘聚力C (kPa)
2）对于路堤填普通土者为： ① 压实后的容重γ（kN/m3） ② 内摩擦角φ（°） ③ 粘聚力C (kPa)
编辑课件
二、、荷载当量高度：
以相等压力的土层厚度来代替荷载。
编辑课件
四、表解法：
用圆弧法进行边坡稳定性分析，计算工作量较大，对 于均质、直线形边坡路堤，滑动面通过坡脚，顶部为水平 并延伸至无限远处，可按表解法进行边坡稳定性分析。
件下的稳定边坡值。
编辑课件
2、力学计算法（理论法）

BD
A 深路堑
沿直线形态 滑动面下滑
D
A
陡坡路堤
假定AD为直线滑动面，并通过坡脚点A，土质均匀，取 单位长度路段，不计纵向滑移时土基的作用力，可简化
成平面问题求解。
一、试算法
由图，按静力平衡得：
K= R N f cL Q cos tan cL
T
T
Q sin
ω——滑动面的倾角；
B
D
f——摩擦系数，f=tanφ;
L——滑动面AD的长度； H
R
N——滑动面的法向分力； T——滑动面的切向分力; c——滑动面上的粘结力； Q——滑动体的重力。
T αω
A
ω
N Q
直线滑动面上的力系示意图
K= R N f cL Q cos tan cL
T
T
Q sin
滑动面位置ω不同
力学分析法：数解方法 ★
似 解
图解法：图解简化
基本方法：
抗滑力
稳定系数 K= R T
<1:边坡不稳定
K =1:极限平衡状态 ＞1:边坡稳定,工程上一般规定K≥1.20~1.25
行车荷载是边坡稳定的主要作用力,换算方法：
行车荷载换算成相当于路基岩土层厚度，计入滑动体的 重力中；换算时按荷载的不利布置条件，取单位长度路段。
Kmin 2a f ctg 2 a f a csc
cotα=0.5,α=63026′ cscα=1.1181 f=tan250=0.4663, a=2c/γH=0.2778
Φ=250， c=14.7kpa, γ=17.64
H=6m
Kmin 2a f ctg 2 a f a csc

路基边坡稳定性分析本设计计算内容为广西梧州绕城高速公路东段k15+400～k16+800路段中出现的最大填方路段。

该路堤边坡高22m，路基宽26m，需要进行边坡稳定性验算。

1.确定本设计计算的基本参数本段路段路堤边坡的土为粘性土，根据《公路路基设计规范》，取土的容重γ=18.5kN/m³，粘聚力C=20kpa，内摩擦角C=24º，填土的内摩擦系数ƒ=tan24º=0.445。

2.行车荷载当量高度换算高度为:25500.8446(m)5.512.818.5NQhBLλ⨯===⨯⨯h0—行车荷载换算高度；L—前后轮最大轴距，按《公路工程技术标准》（JTG B01-2003）规定对于标准车辆荷载为12.8m；Q—一辆车的重力（标准车辆荷载为550kN）；N—并列车辆数，双车道N=2，单车道N=1；γ—路基填料的重度（kN/m3）；B—荷载横向分布宽度，表示如下：(N1)m dB Nb=+-+式中：b—后轮轮距，取1.8m；m—相邻两辆车后轮的中心间距，取1.3m；d—轮胎着地宽度，取0.6m。

3. Bishop法求稳定系数K3.1 计算步骤：（1）按4.5H 法确定滑动圆心辅助线。

由表查得β1=26°，β2 =35°及荷载换算为土柱高度h0 =0.8446(m),得G点。

a .由坡脚A 向下引竖线，在竖线上截取高度H=h+h0（h 为边坡高度，h0 为换算土层高）b.自G 点向右引水平线，在水平线上截取4.5H，得E 点。

根据两角分别自坡角和左点作直线相交于F 点，EF 的延长线即为滑动圆心辅助线。

c.连接边坡坡脚A 和顶点B ，求得AB 的斜度i=1/1.5，据此查《路基路面工程》表4-1得β1,β2。

图1(4.5H 法确定圆心)（2）在CAD 上绘出五条不同的位置的滑动曲线 （3）将圆弧范围土体分成若干段。

（4）利用CAD 功能读取滑动曲线每一分段中点与圆心竖曲线之间的偏角αi (圆心竖曲线左侧为负，右侧为正)以及每分段的面积S i 和弧长L i ； （5）计算稳定系数：首先假定两个条件：a,忽略土条间的竖向剪切力X i 及X i+1 作用；b,对滑动面上的切向力T i 的大小做了规定。

浅蓝色单元格路堤填土高h1：13.31车道数：双向两车道路堤边坡坡率m：1：1.5粘聚力C(KPa):30内摩擦角φ:35°土的容重(KN/m 3)γ:20路基填料的重度(KN/m3)γ:25计算过程如下：2=5.5m因此,=0.625m基本参数填入格 路基稳定性式中：N—并列车辆数，双车道N=2；b —后轮轮距，取1.8m；m —相邻两辆车后轮的中心间距，取1.3m；d —轮胎着地宽度，取0.6m；由于行车荷载对较高路堤边坡稳定性影响较小，为简化计算，将换算高度分布于路基全宽上(2）确定圆弧辅助线位置本例按4.5H法确定滑动圆心辅助线。

B—荷载横向分布宽度：(1）行车荷载换算高度h0按下式计算换算土柱高h0为：式中：L—前后轮最大轴距，按《公路工程技术标准》（JTG B01-2014）规定对于标准车辆荷载为Q—1辆重车的重力（标准车辆荷载为550KN）；γ—路基填料的重度；0NQ h BL γ==(1)B Nb N m d+-+=(1)B Nb N m d +-+0NQ h BL γ=β1=26°β2=35°（4）计算步骤根据4.5H法确定圆心位置，如下图:（3）计算位置选取：①滑动面位于路基左边缘处；②滑动面经过路基中央分隔带边缘；③滑动面位于路基左边缘处:滑动面经过路基中央①　圆弧范围内土体自每土基和填土交点处向二侧每5m一段。

②　在CAD中量取分段中心距圆心竖线的水平距离 ，其中在圆心竖线左侧为负，右侧为正，sin ii x Rα=滑动面在土基内时，法线方向分力：③　计算每个土条的面积。

④　以路堤纵向长度1m计算出各个分段的重力G i ，G j 。

⑤　将每一段的重力G i 、G j 化为二个分力：切线方向分力：根据以上计算步骤得出各种情形的计算结果如下所示。

情形1：滑动面经过距路基左边缘1/4路基宽度处，计算如下表：情形2：滑动面经过距路基中线，计算如下表：cos i i iN G α=sin i i iT G α=L i =44.83mL j =18.62mL i =25.43mL j =38.85m（6）稳定系数计算稳定系数K计算公式为：其中，f=0.700f=tan(φ)情形3：滑动面经过距路基最危险处计算如下表：土条序号1~4滑动面在土基内，其余在路堤内。

4.5H法验算路基稳定性注：本文档为手算计算书文档，包含公式、计算过程在内，可供老师教学，可供学生学习。

下载本文档后请在作者个人中心中下载对应Excel计算过程。

（若还需要相关cad 图纸或者有相关意见及建议，请私信作者！）团队成果，侵权必究！路基稳定性验算对于地质与水文条件复杂、高填深挖、地面坡度陡于1：2.5的边坡，应进行边坡稳定验算。

本路基设计中出现了较高路堤和深路堑，需要进行边坡稳定性验算；同时结合实际情况，选定合理的工程技术措施提高路基稳定性。

高路堤边坡稳定性计算本路线中桩号K2+060处边坡填土高度最大为8.46m，填土高度较大，须进行路堤稳定性验算，验算采用圆弧滑动面条分法进行计算。

基本资料：土质路堤边坡高H=8.46m，设置边坡坡率为：边坡1：1.5；现拟定填土的粘聚力，内摩擦角,容重3，地基土的粘聚力，内摩擦角=，容重3。

计算荷载为公路一I级汽车荷载。

计算过程如下：(1）行车荷载换算高度h0按下式计算换算土柱高h0为：0NQhBLγ=式中：L—前后轮最大轴距，按《公路工程技术标准》（JTG B01-2014）规定对于标准车辆荷载为为12.8m；B—横向分布宽度：=(1)B Nb N m d+-+=2×1.8+（2-1）×1.3+0.6=5.5m因此由于行车荷载对较高路堤边坡稳定性影响较小，为简化计算，将换算高度分布于路基全宽上。

(2）确定圆弧辅助线位置本例按4.5H法确定滑动圆心辅助线。

由上图可知，边坡坡比为1：1.5时，，查规范得1β=26°，2β=35°。

根据4.5H 法确定圆心位置，如下图。

图5-1 4.5H 法确定圆心（3）计算位置选取：①通过路基中线；②通过路基右边缘；③通过距路基右边缘1/4路基宽度处。

图5-2 滑动面经过距路基左边缘1/4路基宽度处。

称瑞典条分法。
简单二条分、法动适态用于弯边沉坡检有不测同的土层、均质土边坡，部分被淹没、均质 土坝，局部发生渗漏、边坡为折线或台阶形的粘性土的路堤与路堑。
三、平整度检测
二、动态弯沉检测 三、平整度检测
二、动态弯沉检测 三、平整度检测
瑞典条分法是所有条分法的雏形。在它的假定中，滑裂面为圆弧面，忽略
孔隙水压二力、的动产生态，弯使沉土体检作测用有动、静水压力，促使土体失稳，故设计斜坡
应针对这些原因，采用相应的排水措施。
（2）三振、动的平作整用度：如检地测震的反复作用下，砂土极易发生液化；粘性土，振
动时易使土的结构破坏，从而降低土的抗剪强度；车辆运动、施工打桩或爆破， 由于振动也可使邻近土坡变形或失稳等。
失稳土体二的、滑动动面态近弯似直沉线检形态测。直线法是假定路基边坡滑坍时，滑动面为
一平面，它适合于砂性类土填筑的路基边坡稳定性计算。原地面为近似直线的
陡坡路堤三，、如果平接整触面度的检摩测擦力不足，整个路堤亦可能沿原地面成直线形态下滑。
二、动态弯沉检测
三、平整 度检测
按照公路的有关设计规范，路堤边坡稳定性必须满足下式：
En<0表示不会产生未平衡的推力，按1.25的安全系数考虑，该折线滑动 面路基是安全的。如果En >0则土体的滑动稳定性不满足要求，必须对土体 采取加固措施。
不二平、衡动推力态法弯在划沉分检土测条后，其计算针对每一土 条分别进行,将上一土
条计算出的剩余滑动力施加在下一土条上，如果计算出的剩余滑动力小于
如此反二复、迭动代，态直弯至前沉后检两测次的Fs值非常接近。通常只要迭代3~4次,就可
以得到满足精度要求的解，而且迭代通常是收敛的。
三、平整度检测
4.圆弧滑动面假定的圆心辅助线的确定方法 1）4.5H法

＝1587.6 13.9 1601.4 Fs 2440.1/1601.4 1.524
稳定性验算
• 计算其他2个滑动面稳定系数 • K1 ＝1.46 ；K3＝1.74 • K>[K]=1.45 满足
§ 4.2 陡坡路堤稳定性
滑动面为多个坡度的折线时，可采用不平衡推 力法进行分析
Ei
WQi sin i
圆弧法例题
圆弧法例题
1、用方格纸以1：50比例绘出路堤横断面。
2、荷载当量土柱高度h0 L=12.8m,
h0

NQ
BL
B=Nb+(N-1)m+d
N=2；d=0.6m，b=1.8m，m=1.3m
B=2×1.8+1.3+0.6＝5.4m
h0=2*800/12.8/5.4/17=1.4m
圆弧法例题
圆弧法简化计算图示
圆弧法－简化Bishop法
• 当土条 i 滑弧位于地基中时
Ki

cdibi
Wditgdi
U (Wdi mi
Qi )tgdi
• Wdi－第i条土条地基部分的重力 • Wti－第i条土条路堤部分的重力 • b i－第i条土条宽度 • c擦di,角φdi－第i条土条滑弧所在地基土层的粘结力和内摩 • U－地基平均固结度 • mαi －系数
2、自F点向右引水平线，在水平线上截取4.5H,得 M点；
3、连坡脚E和顶点S，求SE的斜度i0=1/m；查表 得β1，β2，由E点作与SE成β1角的直线，再由S 点作与水平线成β2角的直线，两线相交得I点；
4、连结I和M两点得圆心辅助线。
4.5H法
36°线法
1、 36°线法一－考虑荷载
2、 36°线法二－不考虑荷载

利用简单条分法进行路基稳定性计算一． 绘出最高填方路基横断面图（见CAD 图）二． 将汽车-20级荷载换算成土柱高，设两辆重车并列，则横向分布宽度可由公式换算得到B 。

在进行路堤稳定性验算时，将车辆荷载按最不利情况排列，并换算成相当的土层厚度。

公路二级汽车荷载换算成土柱高： 由《路基路面工程》有BlnGh γ=0 ；式中：n —并列车辆数 l —标准车辆轴距G—一辆重车的重力γ—路基填料的重度为20KN/m 3； B —荷载横向分布宽度本设计公路为二车道，设计荷载采用：汽车-20，挂车-100，则2n =,KNG 300=,m l 6.5=,6.03.118.12)1(+⨯+⨯=+-+=e d n nb B =m5.5则m h 97.06.55.52030020=⨯⨯⨯=。

三． 路基整体稳定性分析选择最大填土高度为7.12m 的横断面进行稳定性分析。

由资料可知:该路堤填土为低液限粘土，土的重度3m 20KN =γ土的内摩擦角 24=ϕ，黏聚力10=c Kpa 。

为简化计算，可假设破坏面为一圆弧滑动面，采用简单条分法进行计算。

四． 确定圆形辅助线先由4.5H 法确定圆心辅助线位置：10h h H +=，1h 为路基高度，0h 为汽车荷载换算高度。

计算知：H=4.99+0.97=5.96m 加上汽车荷载换算高度后，换算后的边坡坡度为8.09:13.33=1:1.5,查表知352,251==ββ，作图如下，得到0点。

五． 条分法验算路基稳定性土条编号)(b m i )(m x i )( i α)(m l i)(2m A i )(i kN W )(cos kN W i i α (sin kNW i i α1 2.5 12.97 59.98 4.996979 6.12 122.4 63.07255 104.8981 2 2 10.72 45.1 2.833377 11.15 223 157.4096 157.9596 3 2 8.72 35.18 2.446944 14.6 292 238.657 168.2463 4 2 6.72 26.36 2.232088 15.25 305 273.2831 135.4302 5 2 4.72 18.17 2.104963 13.66 273.2 259.5731 85.20576 6 2 2.72 10.35 2.033081 12.06 241.2 237.2724 43.35034 7 2 0.72 2.73 2.002272 9.86 197.2 196.9767 9.381789 8 2 -1.28 -4.85 2.007187 7.16 143.2 142.6869 -12.1115 9 2 -3.28 -12.52 2.048718 5.41 108.2 105.6282 -23.4502 101.95 -5.25 -20.32.079137 2.0140.237.70365-13.9454∑=102i i l24.78474627∑92icos iWα1712.2632i iWαsin ∑654.964989六．。