第4章 知识图谱

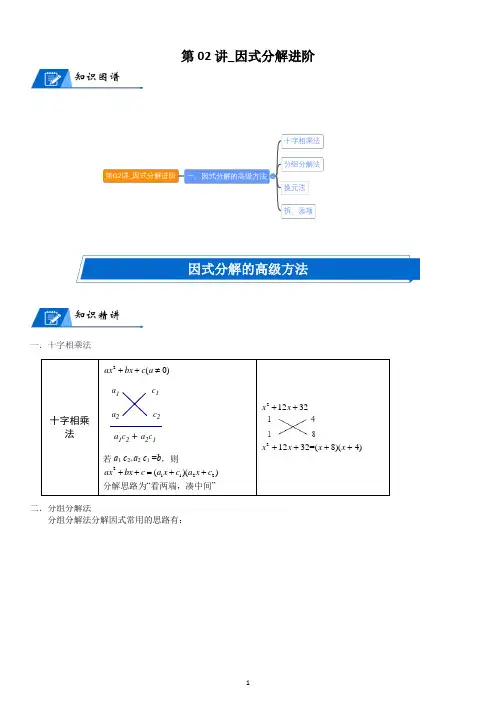
第02讲_因式分解进阶知识图谱因式分解的高级方法知识精讲一．十字相乘法二．分组分解法分组分解法分解因式常用的思路有：十字相乘法 2(0)ax bx c a ++≠ 若a 1 c 2+a 2 c 1 =b ，则 21122()()ax bx c a x c a x c ++=++ 分解思路为“看两端，凑中间” 21232x x ++21232=(8)(4)x x x x ++++a 1a 2c 2c 1a 1c 2 + a 2c 1分组分解法（1）适用场景：不能直接运用提公因式法和公式法（2）方法：把这个多项式分成几组，对各组分别分解因式，然后再对整体作因式分解四项=二项+二项（按字母分组、按系数分组、符合公式的两项分组）四项=三项+一项（先完全平方公式后平方差公式）五项=三项+二项（完全平方公式）六项=三项+三项（完全平方公式）六项=二项+二项+二项（各组之间有公因式）六项=三项+二项+一项（完全平方公式）三．换元法四．拆、添项法三点剖析一．考点：1．十字相乘法；2．分组分解法；3．换元法；4．拆、添项二．重难点：十字相乘法；分组分解法；换元法；拆、添项．三．易错点：（1）正确的十字相乘必须满足以下条件：在上式中，竖向的两个数必须满足关系12a a a =，12c c c =；斜向的两个数必须满足关系1221a c a c b +=，分解思路为“看两端，凑中间．”（2）换元法换元分解因式后，一定要记得将原有的字母换回来，并最终对每一项都彻底因式分解．c 1c 2a 2a 1换元法将一个较复杂的代数式中的某一部分看作一个整体，用一个新字母替代它，简化运算过程设， 则原式易错点：换元分解因式后，一定要记得将原有的字母换回来。

并再次对每一项彻底的因式分解拆、添项（1）在多项式中添上两个符号相反的项，再使用分组分解法进行分解因式（2）将多项式中的某一项拆成两项或多项，再使用分组分解法十字相乘法例题1、 如果把多项式x 2﹣8x+m 分解因式得（x ﹣10）（x+n ），那么m+n=_____________． 【答案】 -18【解析】 ∵x 2﹣8x+m=（x ﹣10）（x+n ）， ∴x 2﹣8x+m=x 2+（﹣10+n ）x ﹣10n ， ∴﹣10+n=﹣8，m=﹣10n ， 解得：n=2，m=﹣20， m+n=﹣20+2=﹣18．例题2、 因式分解：﹣2x 2y+8xy ﹣6y=_______． 【答案】 ﹣2y （x ﹣1）（x ﹣3）【解析】 原式=﹣2y （x 2﹣4x+3）=﹣2y （x ﹣1）（x ﹣3）例题3、 甲、乙两个同学分解因式x 2+ax+b 时，甲看错了b ，分解结果为（x+2）（x+4）；乙看错了a ，分解结果为（x+1）（x+9），则a=__，b=__． 【答案】 6；9【解析】 分解因式x 2+ax+b ，甲看错了b ，但a 是正确的， 他分解结果为（x+2）（x+4）=x 2+6x+8， ∴a=6，同理：乙看错了a ，分解结果为（x+1）（x+9）=x 2+10x+9， ∴b=9，例题4、 因式分解：221999199911999x x .【答案】 ()()199911999x x +- 【解析】 该题考查的是因式分解．十字相乘可得原式()()199911999x x =+- 例题5、 把下列多项式因式分解 （1）22273x xy y -+（2）22675x xy y --【答案】 （1）(3)(2)x y x y --（2）(2)(35)x y x y +-【解析】 （1）22273(3)(2)x xy y x y x y -+=--（2）22675(2)(35)x xy y x y x y --=+- 例题6、 把下列多项式因式分解 （1）2532x x -- （2）2568x x +- （3）26525x x -- （4）26113x x -+【答案】 （1）(52)(1)x x +- （2）(54)(2)x x -+（3）(25)(35)x x -+（4）(23)(31)x x --【解析】 利用十字相乘法进行因式分解可得（1）2532(52)(1)x x x x --=+- （2）2568(54)(2)x x x x +-=-+ （3）26525(25)(35)x x x x --=-+ （4）26113(23)(31)x x x x -+=-- 例题7、 分解因式：2214425x y xy +- 【答案】 ()212x -【解析】 略例题8、 仔细阅读下面例题，解答问题：例题：已知二次三项式x 2－4x ＋m 有一个因式是（x ＋3），求另一个因式以及m 的值． 解：设另一个因式为（x ＋n ），得 x 2－4x ＋m ＝（x ＋3）（x ＋n ）则x 2－4x ＋m ＝x 2＋（n ＋3）x ＋3n ∴343n m n +=-⎧⎨=⎩．解得：n ＝－7，m ＝－21 ∴另一个因式为（x －7），m 的值为－21 问题：仿照以上方法解答下面问题：已知二次三项式2x 2＋3x －k 有一个因式是（2x －5），求另一个因式以及k 的值． 【答案】 另一个因式为（x ＋4），k ＝20 【解析】 设另一个因式为（x ＋a ），得2x 2＋3x －k ＝（2x －5）（x ＋a ） 则2x 2＋3x －k ＝2x 2＋（2a －5）x －5a ∴2535a a k -=⎧⎨-=-⎩解得：a ＝4，k ＝20故另一个因式为（x ＋4），k 的值为20． 随练1、 如果x 2－px ＋q ＝（x ＋1）（x －3），那么p 等于（ ） A.－2 B.2 C.－3 D.3【答案】 B【解析】 已知等式整理得：x 2－px ＋q ＝（x ＋1）（x －3）＝x 2－2x －3， 可得－p ＝－2，q ＝3， 解得：p ＝2．随练2、 分解因式：22268x y x y -++- 【答案】 (4)(2)x y x y -++-【解析】 ()()22222682169x y x y x x y y -++-=++--+()()()()22131313x y x y x y =+--=++-+-+ 随练3、 阅读下列材料，并解答相应问题：对于二次三项式x 2+2ax+a 2这样的完全平方式，可以用公式法将它分解成（x+a ）2的形式，但是，对于一般的二次三项式，就不能直接应用完全平方公式了，我们可以在二次三项式中先加上一项，使其配成完全平方式，再减去这项，使整个式子的值不变，于是有：x 2+2ax ﹣3a 2=x 2+2ax+a 2﹣a 2﹣3a 2=（x+a ）2﹣（2a ）2=（x+3a ）（x ﹣a ） （1）像上面这样把二次三项式分解因式的数学方法是 ； A ．提公因式法 B ．十字相乘法 C ．配方法 D ．公式法 （2）这种方法的关键是 ；（3）用上述方法把m 2﹣6m+8分解因式． 【答案】 （1）B ；（2）利用完全平方公式及平方差公式变形 （3）（m ﹣2）（m ﹣4）【解析】 （1）像上面这样把二次三项式分解因式的数学方法是十字相乘法； （2）这种方法的关键是利用完全平方公式及平方差公式变形； （3）原式=m 2﹣6m+9﹣1=（m ﹣3）2﹣1=（m ﹣3+1）（m ﹣3﹣1）=（m ﹣2）（m ﹣4）， 故答案为：（1）B ；（2）利用完全平方公式及平方差公式变形 随练4、 把下列多项式因式分解 （1）2232x xy y ++ （2）2276x xy y -+ （3）22421x xy y --（4）22215x xy y +-【答案】 （1）()(2)x y x y ++（2）()(6)x y x y --（3）(3)(7)x y x y +-（4）(3)(5)x y x y -+【解析】 （1）()()22322x xy y x y x y ++=++（2）2276()(6)x xy y x y x y -+=-- （3）22421(3)(7)x xy y x y x y --=+-（4）22215(3)(5)x xy y x y x y +-=-+ 随练5、 把下列多项式因式分解 （1）2383x x +- （2）2352x x -+ （3）42627x x -- （4）2236a b a ab +--【答案】 （1）(31)(3)x x -+（2）(32)(1)x x --（3）2(3)(3)(3)x x x -++（4）(2)(13)a b a +-【解析】 （1）2383(31)(3)x x x x +-=-+ （2）2352(32)(1)x x x x -+=--（3）()()()()()4222262793333x x x x x x x --=-+=+-+ （4）()()()()2236232213a b a ab a b a a b a b a +--=+-+=+- 随练6、 把下列多项式因式分解 （1）2273x x -+ （2）2675x x -- （3）4268x x ++（4）2()4()3a b a b +-++【答案】 （1）(3)(21)x x --（2）(21)(35)x x +-（3）22(2)(4)x x ++（4）(1)(3)a b a b +-+- 【解析】 （1）利用十字相乘法进行因式分解得（1）2273(3)(21)x x x x -+=-- （2）2675(21)(35)x x x x --=+- （3）422268(2)(4)x x x x ++=++（4）2()4()3(1)(3)a b a b a b a b +-++=+-+-分组分解法例题1、 已知：a 2＋b 2＋c 2－ab －ac －bc ＝0，则a 、b 、c 的大小关系为________． 【答案】 a ＝b ＝c【解析】 ∵a 2＋b 2＋c 2－ab －bc －ac ＝0， ∵2a 2＋2b 2＋2c 2－2ab －2bc －2ac ＝0，a 2＋b 2－2ab ＋b 2＋c 2－2bc ＋a 2＋c 2－2ac ＝0， 即（a －b ）2＋（b －c ）2＋（c －a ）2＝0， ∵a －b ＝0，b －c ＝0，c －a ＝0， ∵a ＝b ＝c ．例题2、 已知a=998，b=997，c=996，则a 2﹣ab ﹣ac+bc=______________． 【答案】 2【解析】 原式=a （a ﹣b ）﹣c （a ﹣b ） =（a ﹣b ）（a ﹣c ） =（998﹣997）（998﹣996） =1×2 =2，例题3、 分解因式a 2﹣b 2﹣2b ﹣1=__________． 【答案】 （a+b+1）（a ﹣b ﹣1）． 【解析】 a 2﹣b 2﹣2b ﹣1 =a 2﹣（b 2+2b+1） =a 2﹣（b+1）2 =（a+b+1）（a ﹣b ﹣1）．例题4、 把下列多项式因式分解 （1）224484a b a b ab +-+-（2）222xy xz y yz z --+-【答案】 （1）(2)(24)a b a b ---（2）()()y z x y z --+【解析】 （1）()()()()()()2222244844448242224a b a b ab a ab b a b a b a b a b a b +-+-=-+--=---=---（2）()()()()2222xy xz y yz z x y z y z y z x y z --+-=---=--+例题5、 仔细阅读下列解题过程：若a 2＋2ab ＋2b 2－6b ＋9＝0，求a 、b 的值． 解：∵a 2＋2ab ＋2b 2－6b ＋9＝0 ∴a 2＋2ab ＋b 2＋b 2－6b ＋9＝0 ∴（a ＋b ）2＋（b －3）2＝0 ∴a ＋b ＝0，b －3＝0 ∴a ＝－3，b ＝3根据以上解题过程，试探究下列问题：（1）已知x 2－2xy ＋2y 2－2y ＋1＝0，求x ＋2y 的值； （2）已知a 2＋5b 2－4ab －2b ＋1＝0，求a 、b 的值；（3）若m ＝n ＋4，mn ＋t 2－8t ＋20＝0，求n 2m －t 的值． 【答案】 （1）3 （2）a ＝2；b ＝1 （3）1【解析】 （1）∵x 2－2xy ＋2y 2－2y ＋1＝0 ∴x 2－2xy ＋y 2＋y 2－2y ＋1＝0 ∴（x －y ）2＋（y －1）2＝0 ∴x －y ＝0，y －1＝0， ∴x ＝1，y ＝1， ∴x ＋2y ＝3；（2）∵a 2＋5b 2－4ab －2b ＋1＝0 ∴a 2＋4b 2－4ab ＋b 2－2b ＋1＝0 ∴（a －2b ）2＋（b －1）2＝0 ∴a －2b ＝0，b －1＝0 ∴a ＝2，b ＝1； （3）∵m ＝n ＋4，∴n （n ＋4）＋t 2－8t ＋20＝0 ∴n 2＋4n ＋4＋t 2－8t ＋16＝0 ∴（n ＋2）2＋（t －4）2＝0 ∴n ＋2＝0，t －4＝0 ∴n ＝－2，t ＝4 ∴m ＝n ＋4＝2∴n 2m －t ＝（－2）0＝1．例题6、 阅读下列文字与例题：将一个多项式分组后，可提公因式或运用公式继续分解的方法称作分组分解． 例如：以下两个式子的分解因式的方法就称为分组分解法．（1）am+an+bm+bn=（am+bm ）+（an+bn ）=m （a+b ）+n （a+b ）=（a+b ）（m+n ）； （2）x 2﹣y 2﹣2y ﹣1=x 2﹣（y 2+2y+1）=x 2﹣（y+1）2=（x+y+1）（x+y ﹣1） 试用上述方法分解因式： （1）a 2+2ab+b 2+ac+bc （2）4a 2﹣x 2+4xy ﹣4y 2． 【答案】 （1）（a+b ）（a+b+c ）（2）（2a+x ﹣2y ）（2a ﹣x+2y ）【解析】 （1）原式=（a 2+2ab+b 2）+（ac+bc ）=（a+b ）2+c （a+b ）=（a+b ）（a+b+c ）； （2）原式=4a 2﹣（x 2﹣4xy+4y 2）=4a 2﹣（x ﹣2y ）2=（2a+x ﹣2y ）（2a ﹣x+2y ）． 例题7、 把下列多项式因式分解 （1）251539a m am abm bm -+-（2）432x x x x +++（3）432433x x x x ++++ （4）22ax bx bx ax a b -+-+-（5）2223(1)()22x x xy y x y xy +-+++（6）222x x y xy x y y -+-+-【答案】 （1）()()353m a a b -+；（2）()()211x x x ++；（3）()()2213xx x +++；（4）()()21a b x x --+；（5）()222(1)x x xy y +++；（6）()()21y x x y --+【解析】 （1）()()()()2515395333353a m am abm bm m a a b a m a a b -+-=-+-=-+⎡⎤⎣⎦ （2）()()()()432321111x x x x x x x x x x x +++=+++=++ （3）()()()43243222243333313x x x x x x x x x xx x ++++=+++++=+++（4）()()()()22221ax bx bx ax a b x a b x a b a b a b x x -+-+-=---+-=--+（5）()()2223222222(1)()22(1)2(1)x x xy y x y xy x x xy y xy x x xy y +-+++=+-++=+++ （6）()()()()()222221111x x y xy x y y x y x y y y y x x y -+-+-=---+-=--+ 随练1、 分解因式：y+y 2+xy+xy 2=______． 【答案】 y （1+y ）（1+x ）【解析】 先进行分组，再用提公因式法进行因式分解，即可解答． 解：y+y 2+xy+xy 2=（y+y 2）+（xy+xy 2） =y （1+y ）+xy （1+y ） =（1+y ）（y+xy ） =y （1+y ）（1+x ）．随练2、 分解因式：3232x x y y +-- 【答案】 22()()x y x x xy y y -++-+【解析】 原式33222222()()()()()()()()x y x y x y x xy y x y x y x y x x xy y y =-+-=-++++-=-++-+ 随练3、 分解因式：43221x x x x ++++ 【答案】 22(1)(1)x x x +++【解析】 原式432222222()(1)(1)(1)(1)(1)x x x x x x x x x x x x x =+++++=+++++=+++ 随练4、 把下列多项式因式分解 （1）2214497x xy y x y -++- （2）222(2)123(3)m n mn n m +--- 【答案】 （1）(7)(71)x y x y --+ （2）(23)(23)m n m n mn --+【解析】 （1）()()()()2221449777771x xy y x y x y x y x y x y -++-=-+-=--+ （2）()()2222222(2)123(3)234129m n mn n m m n mn m mn n +---=-+-+()()()()223232323mn m n m n m n mn m n =-+-=-+-随练5、 把下列多项式因式分解（1）2222x x y xy x y y -+-+- （2）222ax by cx ay bx cy ++--- （3）222221a b c c ab +---- （4）222494126x y z xy yz xz ++--+ 【答案】 （1）()(1)(1)x y y x ---（2）()(2)a b c x y -+-（3）(1)(1)a b c a b c -++---（4）2(23)x y z -+ 【解析】 （1）()()()22222222x x y xy x y y x y x y xy x y -+-+-=-----()()()()()()()11x y x y xy x y x y x y x y y =+-----=----⎡⎤⎣⎦()()()11x y y x =---（2）()()222222ax by cx ay bx cy ax bx cx by ay cy ++---=-++--()()()()22x a b c y a b c a b c x y =-+--+=-+-（3）()()()()222222222212211a b c c ab a ab b c c a b c +----=-+-++=--+(1)(1)a b c a b c =-++--- （4）()222249412623x y z xy yz xz x y z ++--+=-+随练6、 把下列多项式因式分解 （1）222xy xz y yz z --+- （2）222222x y xz z a ay --+-- （3）22(3)(34)a b b a --- （4）2(1)1x x x ----【答案】 （1）()()y z x y z --+（2）()()x z a y x z a y -++---（3）(2)(32)a b a -+（4）2(1)(1)x x -+ 【解析】 （1）()()()()2222xy xz y yz z x y z y z y z x y z --+-=---=--+ （2）()()()()22222222222222x y xz z a ay x xz z y ay a x z y a --+--=-+-++=--+ ()()x z a y x z a y =-++---（3）()()2222(3)(34)62346342a b b a a b ab a a ab a b ---=--+=-+-()()()()3222232a a b a b a b a =-+-=-+（4）()()()()()()2233222(1)1111111x x x x x x x x x x x x x x ----=-++-=-+-=-+-=-+ 随练7、 把下列多项式因式分解 （1）23442x x x -+- （2）24263a ab a b +++ （3）2244a b a b -+- （4）22944a ab b ---（5）2221693025m a ab b -+-（6）22194m n mn -++（7）224252036x y xy +--【答案】 （1）()()()2212x x x x --+-+（2）(23)(2)a a b ++（3）()(4)a b a b -++（4）(32)(32)a b a b ++--（5）(435)(435)m a b m a b +--+ （6）11(3)(3)22m n m n +++-（7）(256)(256)x y x y -+-- 【解析】 （1）()()()()()()2234222242422212x x x x x x x x x x x xx -+-=--=+--+=--+-+（2）()()()()242632232223a ab a b a a b a b a b a +++=+++=++ （3）()()()()()224444a b a b a b a b a b a b a b -+-=+-+-=-++（4）()()()222944923232a ab b a b a b a b ---=-+=++--（5）()()()2222216930251635435435m a ab b m a b m a b m a b -+-=--=+--+ （6）222111199334222m n mn m n m n m n ⎛⎫⎛⎫⎛⎫-++=+-=+++- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭ （7）()()()22=256256256x y x y x y --=-+--换元法例题1、 若实数a ，b 满足（2a ＋2b ）（2a ＋2b －2）－8＝0，则a ＋b ＝________． 【答案】 －1或2【解析】 设a ＋b ＝x ，则由原方程，得 2x （2x －2）－8＝0，整理，得4x 2－4x －8＝0，即x 2－x －2＝0， 分解得：（x ＋1）（x －2）＝0， 解得：x 1＝－1，x 2＝2．则a ＋b 的值是－1或2．例题2、 分解因式：22()(32349)x x x x -+--+ 【答案】 223()1x x -- 【解析】 22222223234()()(9326329())3(1)x x x x x x x x x x -+--+=-+--++=-- 例题3、 分解因式：（1）2(3)5(3)14p p ---- （2）()()224341256xx x x -+--+【答案】 （1）(10)(1)p p --（2）2(1)(5)(44)x x x x +---【解析】 （1）()()()()()()2235314353143732p p p p p p ----=----=---+()()101p p =-- （2）()()()()22222434125649420x x x x x x x x -+--+=---+()()()()()22244455144x x x x x x x x =----=-+--例题4、 分解因式：（1）2(3)5(3)14p p ----（2）()()224341256x x x x -+--+（3）22(815)(87)15x x x x +++++（4）22(1)(2)12x x x x ++++- 【答案】 （1）(10)(1)p p --（2）2(1)(5)(2)x x x +--（3）2(2)(6)(810)x x x x ++++（4）2(1)(2)(5)x x x x -+++ 【解析】 （1）()()()()()()2235314353143732p p p p p p ----=----=---+()()101p p =--（2）()()()()22222434125649420x x x x x x x x -+--+=---+()()()()()22244455144x x x x x x x x =----=-+--（3）()()()()2222281587158228120x x x x x x x x +++++=++++()()()()()22281081226810x x x x x x x x =++++=++++（4）()()()()222221212310x x x x x x x x ++++-=+++-()()()()()22252215x x x x x x x x =+++-=+-++随练1、 已知实数x ，y 满足（x 2＋y 2）（x 2＋y 2－12）＝45，求x 2＋y 2的值． 【答案】 15【解析】 设x 2＋y 2＝a ，则a （a －12）＝45， a 2－12a －45＝0， （a －15）（a ＋3）＝0， a 1＝15，a 2＝－3， ∵x 2＋y 2＝a≥0， ∴x 2＋y 2＝15．随练2、 (2013初二上期中人民大学附属中学)因式分解：222618680x xx x【答案】 ()()()224410x x x x ++++． 【解析】 该题考查的是因式分解． 令26x x a +=，则原式21880a a =++ ()()810a a =++()()2268610x x x x =++++()()()224410x x x x =++++随练3、 因式分解：222618680x xx x【答案】 ()()()224410x x x x ++++．【解析】 该题考查的是因式分解． 令26x x a +=， 则原式21880a a =++ ()()810a a =++()()2268610x x x x =++++ ()()()224410x x x x =++++ 随练4、 分解因式：（1）22(815)(87)15x x x x +++++ （2）22(1)(2)12x x x x ++++-【答案】 （1）2(2)(6)(810)x x x x ++++（2）2(1)(2)(5)x x x x -+++ 【解析】 （1）()()()()2222281587158228120x x x x x x x x +++++=++++()()()()()22281081226810x x x x x x x x =++++=++++（2）()()()()222221212310x x x x x x x x ++++-=+++-()()()()()22252215x x x x x x x x =+++-=+-++拆、添项例题1、 分解因式441x +【答案】 22(221)(221)x x x x ++-+ 【解析】()()()()224422222414414212212212x x x x x x x x x x +=++-=+-=+++-例题2、 分解因式：42471x x -+ 【答案】 22(71)(71)x x x x ++-+【解析】 ()()()()22424222224712149171717x x x x x x x x x x x -+=++-=+-=+++-例题3、 分解因式：841x x ++【答案】 2242(1)(1)(1)x x x x x x ++-+-+【解析】 原式844424424221(1)(1)(1)x x x x x x x x x =++-=+-=++-+2242(1)(1)(1)x x x x x x =++-+-+例题4、 分解因式：32265x x x +-- 【答案】 (1)(3)(2)x x x ++-【解析】 3232226566(1)(3)(2)x x x x x x x x x x x +--=+++--=++-例题5、 分解因式)()()(222y x z x z y z y x -+-+- 【答案】 ))()((z x y x z y ---【解析】 22222222()()()=()()()=()()()x y z y z x z x y x y z z x y x y z z y y z x y x z -+-+--+-+----随练1、 分解因式：343a a -+【答案】2(1)(3)a a a -+- 【解析】 332224333(1)(3)a a a a a a a a a a -+=-+--+=-+-随练2、 分解因式：224414x y x y -++【答案】 2222(4)(4)x y xy x y xy +++-【解析】 ()()22224442242222142164x y x y x x y y x y x y xy -++=++-=+-()()222244x y xy x y xy =+++-随练3、 分解因式：4414x y +【答案】 222211()()22x y xy x y xy +++- 【解析】 ()224442242222111442x y x x y y x y x y xy ⎛⎫+=++-=+- ⎪⎝⎭22221122x y xy x y xy ⎛⎫⎛⎫=+++- ⎪⎪⎝⎭⎝⎭随练4、 分解因式：4231x x -+【答案】22(1)(1)x x x x +--- 【解析】 拆项法：原式=422222[()(1)](1)(1)x x x x x x x x ----=+--- 随练5、 分解因式：4224a ab b ++【答案】 2222()()a ab b a ab b ++-+【解析】 添项法：原式=2422422a a b b a b ++-随练6、 分解因式：432234232a a b a b ab b ++++【答案】222()a ab b ++ 【解析】 43223443222234232222a a b a b ab b a a b a b a b ab b ++++=+++++()()4224222222a a b b ab a b a b =+++++()()()22222222222a b ab a b a b a b ab =++++=++随练7、 分解因式：（1）()()22ax by bx ay ++-（2）()(2)(1)(1)x y x y xy xy xy +++++-【答案】 （1）2222()()a b x y ++（2）(1)(1)(1)x y x y xy ++++-【解析】 （1）()()222222222222ax by bx ay a x abxy b y b x abxy a y ++-=+++-+()()()()2222222222x a b y a b a b x y =+++=++（2）()()()()211x y x y xy xy xy +++++-()()()()222211x y xy x y xy x y xy =++++-=++-()()()()()11111x y xy x y xy x y x y xy =+++++-=++++-拓展1、 因式分解 （1）3x ﹣12x 2 （2）x 2﹣9x ﹣10（3）x 2﹣2xz+z 2﹣4y 2（4）25（m+n ）2﹣4（m ﹣n ）2． 【答案】 （1）3x （1﹣4x ）（2）（x ﹣10）（x+1）（3）（x ﹣z+2y ）（x ﹣z ﹣2y ）（4）（7m+3n ）（3m+7n ） 【解析】 （1）原式=3x （1﹣4x ）； （2）原式=（x ﹣10）（x+1）；（3）原式=（x ﹣z ）2﹣4y 2=（x ﹣z+2y ）（x ﹣z ﹣2y ）；（4）原式=[5（m+n ）+2（m ﹣n ）][5（m+n ）﹣2（m ﹣n ）] =（7m+3n ）（3m+7n ）． 2、 因式分解 ①3p 2﹣6pq ②2x 2+8x+8③a 2（x ﹣y ）+16（y ﹣x ） ④x 2﹣2x ﹣15．【答案】 ①3p （p ﹣2q ）， ②2（x+2）2 ③（x ﹣y ）（a+4）（a ﹣4） ④ （x ﹣5）（x+3）【解析】 ①3p 2﹣6pq=3p （p ﹣2q ）；②2x 2+8x+8=2（x 2+4x+4）=2（x+2）2； ③a 2（x ﹣y ）+16（y ﹣x ） =（x ﹣y ）（a 2﹣16） =（x ﹣y ）（a+4）（a ﹣4）； ④x 2﹣2x ﹣15=（x ﹣5）（x+3）． 3、 因式分解：3232x x x ++. 【答案】 ()()12x x x ++【解析】 该题考查的是因式分解．把一个多项式化为几个最简整式的积的形式，这种变形叫做因式分解，也叫做分解因式． 3232x x x ++()232x x x =++()()12x x x =++4、 分解因式：22672x xy y -+ 【答案】 （3x -y ）（x -2y ） 【解析】 （3x -y ）（x -2y ）5、 把下列多项式因式分解 （1）22568x xy y +- （2）2232x xy y -+ （3）2263x x +-（4）2815x x -+【答案】 （1）(2)(54)x y x y +-（2）()(2)x y x y --（3）(9)(7)x x +-（4）(3)(5)x x -- 【解析】 （1）22568(2)(54)x xy y x y x y +-=+-（2）()()22322x xy y x y x y -+=-- （3）()()226397x x x x +-=+-（4）()()281535x x x x -+=--6、 分解因式：x 3﹣5x 2y ﹣24xy 2= ． 【答案】 x （x+3y ）（x ﹣8y ） 【解析】 x 3﹣5x 2y ﹣24xy 2 =x （x 2﹣5xy ﹣24y 2） =x （x+3y ）（x ﹣8y ） 故答案为：x （x+3y ）（x ﹣8y ）．7、 分解因式：2212x x y ---+ 【答案】 (1)(1)y x y x ++--【解析】 原式2222(12)(1)(1)(1)y x x y x y x y x =-++=-+=++--8、 把22222222448a b c d a c b d abcd +--+因式分解． 【答案】 (22)(22)ab cd ac bd ab cd ac bd ++-+-+【解析】 ()()22222222222222224484444a b c d a c b d abcd a b abcd c d a c abcd b d +--+=++--+ ()()2222(22)(22)ab cd ac bd ab cd ac bd ab cd ac bd =+--=++-+-+9、 分解因式：3254222x x x x x --++- 【答案】 42(2)(1)x x x -+-【解析】 原式32542442(2)(2)(2)(2)(2)(2)(2)(1)x x x x x x x x x x x x x =---+-=---+-=-+- 10、 把下列多项式因式分解（1）224484a b a b ab +-+-（2）4322221a a a a ++++【答案】 （1）(2)(24)a b a b ---（2）22(1)(1)a a ++【解析】 （1）()()222244844448a b a b ab a ab b a b +-+-=-+--()()2242a b a b =---()()224a b a b =---（2）()()()()243242222221212111a a a a a a a a a a ++++=++++=++11、 把下列多项式因式分解（1）22ax bx bx ax a b -+-+-（2）432433x x x x ++++（3）2222424a b c d ab cd +--++（4）2269261x xy y x y ++--+ 【答案】 （1）()()21a b x x --+；（2）()()2213x x x +++；（3）(2)(2)a b c d a b c d ++-+-+；（4）2(31)x y +-【解析】 （1）()()()()22221ax bx bx ax a b x a b x a b a b a b x x -+-+-=---+-=--+ （2）()()()43243222243333313x x x x x x x x x x x x ++++=+++++=+++ （3）()()()()222222424222a b c d ab cd a b c d a b c d a b c d +--++=+--=++-+-+（4）()()()222269261323131x xy y x y x y x y x y ++--+=+-++=+- 12、 把下列多项式因式分解（1）242363ax bx x ay by y -+-+- （2）224484a b a b ab +-+- （3）5432221x x x x x +--++（4）228166249x xy y x y -++-+ 【答案】 （1）(21)(23)a b x y -+-（2）(2)(24)a b a b ---（3）32(1)(1)x x +-（4）2(43)x y -+ 【解析】 (1)()()()()2423632213212123ax bx x ay by y x a b y a b a b x y -+-+-=-+--+=-+-(2)()()()()()()2222244844448242224a b a b ab a ab b a b a b a b a b a b +-+-=-+--=---=---(3)()()()()()2543242232221121111(1)(1)x x x x x x x x x x x x x x +--++=+-+++=+-=+-(4)()()()22228166249464943x xy y x y x y x y x y -++-+=-+-+=-+13、 把下列多项式因式分解 （1）1xy x y --+ （2）325153x x x --+ （3）27321x y xy x -+- （4）(1)(2)6x x x --- （5）222(1)()ab x x a b +++（6）215430bm bn am an -+-（7）233a a ab b --+【答案】 （1）()()11y x --；（2）()()2351x x --；（3）()()37x x y -+；（4）()()232x x -+；（5）()()ax b bx a ++；（6）()()2215b a m n +-；（7）()()3a b a -- 【解析】 （1）()()()()()()111111xy x y xy x y x y y y x --+=---=---=-- （2）()()()()()()32322251535153533351x x x x x x x x x x x --+=---=---=-- （3）()()()()()()227321721373337x y xy x x x xy y x x y x x x y -+-=-+-=-+-=-+（4）()()()()()()323222(1)(2)632632632332x x x x x x x x x x x x x x ---=-+-=-+-=-+-=-+ （5）()()()()()()222222(1)()ab x x a b abx b x a x ab bx ax b a ax b ax b bx a +++=+++=+++=++ （6）()()215430241530bm bn am an bm am bn an -+-=+-+ ()()()()221522215m b a n b a b a m n =+-+=+-（7）()()()()()()22333333a a ab b a ab a b a a b a b a b a --+=---=---=--14、 把下列多项式因式分解（1）2c abcd ac bd -+-（2）5432222a a a a a +++++ （3）54ax ax ax a -+-（4）2ax ay a bx by ab -++-+ （5）2293x x y y ---（6）2222x y z yz --+【答案】 （1）(1)(1)ac bd +-（2）23(1)(2)a a a +++（3）4(1)(1)a x x -+ （4）()()x y a a b -++（5）(3)(31)x y x y +--（6）()()x y z x y z +--+【解析】 （1）()()()()21c abcd ac bd c bd ac c bd c bd ac -+-=-+-=-+ （2）()()()()54323222322212112a a a a a a a a a a a a a +++++=+++++=+++ （3）()()()()54441111ax ax ax a ax x a x a x x -+-=-+-=-+（4）()()()()()2ax ay a bx by ab x a b y a b a a b a b x y a -++-+=+-+++=+-+（5）()()()()()()()22229393333331x x y y x y x y x y x y x y x y x y ---=--+=+--+=+-- （6）()()()()2222222222x y z yz x y yz z x y z x y z x y z --+=--+=--=+--+ 15、 若m ＝4n ＋3，则m 2－8mn ＋16n 2的值是________． 【答案】 9【解析】 ∵m ＝4n ＋3， ∴m －4n ＝3，则原式＝（m －4n ）2＝32＝9．16、 分解因式：()()x x x x 2232349-+--+【答案】 ()2231x x --【解析】 2222222(32)(34)9(32)6(32)9(31)x x x x x x x x x x -+--+=-+--++=--17、 因式分解：()()222618680x x x x ++++【答案】 ()()()224610x x x x ++++．【解析】 令26x x a +=，则原式21880a a =++()()810a a =++()()2268610x x x x =++++()()()224610x x x x =++++18、 分解因式41)42)(52(22++---x x x x 【答案】 ()()()21322x x x x +--+ 【解析】 本题考查的是因式分解． 设22y x x =-，上式()()5414y y =-++， 整理得：上式26y y =--十字相乘法得：上式()()32y y =-+．把22y x x =-代入得：()()222322x x x x ---+十字相乘法得：上式()()()21322x x xx =+--+19、 因式分解： （1）222618680x xx x（2）()()x x x x 2232349-+--+【答案】 （1）()()()224610x x x x ++++；（2）()2231x x --【解析】 （1）令26x x a +=，则原式21880a a =++()()810a a =++()()2268610x x x x =++++=()()()224610x x x x ++++（2）2222222(32)(34)9(32)6(32)9(31)x x x x x x x x x x -+--+=-+--++=--20、 分解因式：（1）224414x y x y -++（2）841x x ++【答案】 2222(4)(4)x y xy x y xy +++-；2242(1)(1)(1)x x x x x x ++-+-+ 【解析】 （1）()()22224442242222142164x y x y x x y y x y x y xy -++=++-=+-()()222244x y xy x y xy =+++-（2）848442242121(1)(1)(1)x x x x x x x x x x x ++=++-=++-+-+21、 分解因式：464x +【答案】22(84)(84)x x x x +++- 【解析】()()()()22442222264166416848484x x x x x x x x x x +=++-=+-=+++-22、 分解因式：3234x x +-【答案】 2(1)(2)x x --【解析】 323222344444(1)(2)x x x x x x x x x +-=-+-+-=--23、 分解因式：12631x x -+ 【答案】 6363(1)(1)x x x x -+++【解析】()()()()2212612666363633121111x x x x x x x x x x x -+=-+-=--=-+++24、 分解因式：444222222222a b c a b b c c a ---+++ 【答案】 ()()()()c a b c a b a b c a b c -+--++++- 【解析】 444222222222a b c a b b c c a ---+++ 22444222222222222222222222242224()(2)(2)()()()()a b a b c b c c a a b a b a b c a b a b c a b a b c c a b c a b a b c a b c =---++-=-+-=++---+=-+--++++-25、 分解因式：3)5)(3(22-----x x x x 【答案】 (1)(2)(2)(3)x x x x ++-- 【解析】22222(3)(5)3(3)2(3)3(1)(2)(2)(3)x x x x x x x x x x x x -----=------=++-- 26、 分解因式2222(48)3(48)2x x x x x x ++++++【答案】 ()()()22458x x x x ++++【解析】()()()()22222248348248482x x x x x x x x x x x x ++++++=++++++()()()22458x x x x =++++。

知识图谱技术在教育信息化中的应用研究第一章：绪论教育信息化是指运用信息技术手段优化教育过程和教育资源的传播、管理和应用的过程。

一方面，教育信息化可以提高教育信息的传递速度和效率，另一方面，通过信息化手段，可以将教育资源更好地整合和共享，促进教育均衡发展。

而作为信息技术的重要分支之一，知识图谱技术能够帮助教育信息化更好地发展，提高教育资源的利用效率。

第二章：知识图谱技术简介知识图谱技术（Knowledge Graph）是一种基于语义网的语义网络。

它能够将不同领域的知识点联系起来，建立一个庞大且互相关联的知识图谱，并能够将知识点之间的关系进行推导分析。

在数据处理和语义理解方面，知识图谱技术具有非常广泛的应用前景。

目前，Google、IBM、微软、阿里巴巴等大型企业和机构都在积极探索和应用这项技术。

第三章：知识图谱技术在教育信息化中的应用1.知识管理知识图谱技术可以将零散的知识点进行整合，形成结构化的知识体系。

在教育信息化中，可以将教材中的知识点和学生的知识积累进行结合，建立一个全局的知识库。

通过这样的方式，教师可以更好地规划教学，并能够更加有针对性地进行教育资源的选择和优化。

2.教学辅助知识图谱技术可以将各个知识点之间的内在联系进行明确，并能够推断出一些未被直接表达的知识关系。

在教学过程中，学生在学习某个知识点的同时，可以看到与之相关的其他知识点，更好地了解知识间的内在关系。

同时，知识图谱技术能够根据学生的学习情况，推荐给学生一些相关的知识点，帮助学生更加深入地掌握所学的知识。

3.学生评估知识图谱技术可以通过对学生学习历程的分析，判断学生是否掌握了所学的知识点；同时还能够比较不同学生之间的学习情况，从而确定每个学生的优势和不足。

借助这些数据，教师可以做出更加准确的评估和辅导，帮助学生更好地发挥自己的潜力。

4.教学资源整合知识图谱技术可以将不同的教学资源整合在一起，为学生提供更加丰富和全面的教学体验。

+《知识图谱》++赵军刘康何世柱陈玉博编著+《知识图谱》是知识图谱领域的入门教材，围绕知识建模、知识获取、知识融合、存储和 I 检索、知识推理以及知识服务等知识图谱生命周期各个主要环节展开介绍。

每部分内容 J 以任务为导引.引出任务描述、难点问题、基本方法、研 J 究现状和存在的问题.并从多个相关的研究方向对各个 ;任务的发展进程进行系统的、多维度的梳理.注重尽量 I 全面地介绍传统知识工程、机器学习、深度学习在知识 ;图谱各个环节中的应用.从而使读者能够了解知识图谱 ;的发展脉络，激发研究兴趣，思考核心问题，领悟发展 i 方向。

t; 该书充分参考并吸收国内外代表性的研究工作，在;对知识图谱生命周期各个环节进行系统梳理的基础上， ［撰写形成书中的主要内容。

全书共10章.第1章是绪 ］论.主要对知识图谱的定义、发展历程、类型和主要生命 ;周期进行介绍，并介绍了知识图谱与深度学习的关系，；使读者全面了解相关内容；第2章介绍知识表示，包含经典的知识表示理论、语义网中的； 1知识表示方法.以及知识图谱中符号和数值化的表示方法，本章是知识图谱的核心基础；I I t ；第3章介绍知识体系构建和知识融合；第4〜7章分别讲述实体识别、实体消歧、关系抽； « «;取、事件抽取等不同层级、不同粒度知识自动获取任务.它们是知识图谱构建的主要技术；; ；第8章介绍知识图谱的存储和检索，是知识图谱数据管理的主要任务：第9章讲述知识推］ ；理.这是人工智能的核心任务之一；第10章以问答和对话两种典型系统介绍知识图谱的］ ［主要应用。

；该书可以作为知识工程、自然语言处理、人工智能等相关课程的研究生教材.也可供］ t 计算机科学技术领域相关工程技术人员学习参考。

++" +“ 一-+“+--♦---“ + -----------------------------»-----------+ “+“+”- -----“+ -----1-----“+ “ -----------»-----”-*-------------»---------------•••*。

知识图谱中的实体消歧与链接技术研究第一章知识图谱简介知识图谱是一种将信息进行链接、加工、整理的语义网络结构。

知识图谱不仅仅将各种信息进行关联，而且也赋予了信息更多的意义和价值。

知识图谱由实体、关系和属性三部分组成。

其中，实体是指一切事物，包括人、组织、地点、事件等等。

关系指实体之间的相互作用和联系，例如 A 和 B 之间可能有物理上的联系、亲属关系或者其他的各种关系。

属性则是描述实体和关系的特征和特性。

在构建知识图谱的过程中，实体消歧与链接技术便显得尤为重要和必须。

第二章实体消歧实体消歧是指在大规模文本语料中，从同名实体中，准确的将其指代的实体所在位置判断出来的技术。

大规模文本语料中常常存在同名的实体，而且这些实体可能代码相同的个体，也可能是不同的个体。

链球各种同名实体遍布在大规模文本语料中，难以确认它的确切含义和指向。

针对同名实体的存在，实体消歧技术应运而生。

实体消歧技术可以分为基于数据库的方法、基于语义相似度的方法和基于上下文的方法三类。

2.1 基于数据库的方法基于数据库的方法常常是指利用各种知名实体库或者百科全书进行实体消歧，通过数据库中的大量信息来确定实体是否为同名实体。

在采用基于数据库的方法进行实体消歧时，需要小心处理实体库中可能存在的不一致性、实体库中信息的缺失和错误等问题。

2.2 基于语义相似度的方法基于语义相似度的实体消歧技术主要利用词汇的相似性或语义相似度来判断实体是否为同名实体，通常利用词汇语义的相似性来进行判断，例如 WordNet 数据库的种种词汇语义信息。

2.3 基于上下文的方法使用上下文信息进行实体消歧，是一种常见和高效的实体消歧技术。

上下文可以包括实体所在文本的上下文信息，或者实体所在文本的词性、实体特征的词性等等。

第三章实体链接实体链接是将文本中的实体与知识图谱中的实体进行链接的过程。

实体链接技术通常包括实体识别，实体消歧，和实体映射。

3.1 实体识别实体识别是将文本中出现的实体进行识别的过程。

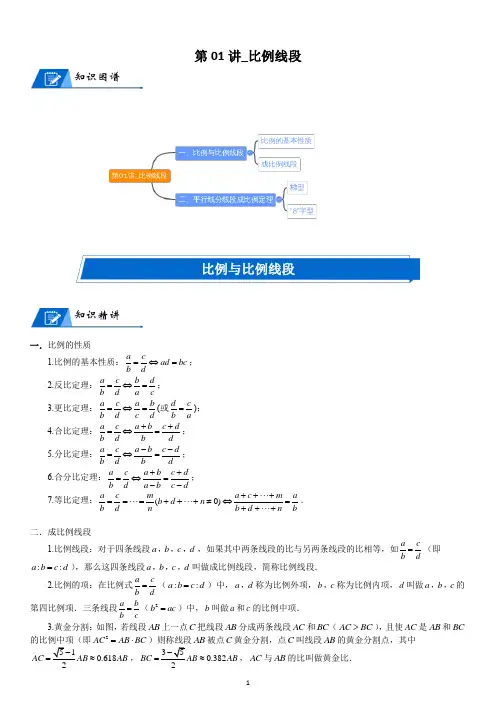
第01讲_比例线段知识图谱比例与比例线段知识精讲一．比例的性质1.比例的基本性质：a cad bc b d =⇔=； 2.反比定理：a c b db d ac =⇔=；3.更比定理：a c a b b d c d =⇔=(或d cb a =)；4.合比定理：a c a b c db d b d ++=⇔=； 5.分比定理：a c a b c db d b d --=⇔=； 6.合分比定理：a c a b c db d a bcd ++=⇔=--； 7.等比定理：(0)a c m a c m ab d n b d n b d n b++⋅⋅⋅+==⋅⋅⋅=++⋅⋅⋅+≠⇔=++⋅⋅⋅+．二．成比例线段1.比例线段：对于四条线段a b c d ，，，，如果其中两条线段的比与另两条线段的比相等，如a cb d=（即::a b c d =），那么这四条线段a b c d ，，，叫做成比例线段，简称比例线段． 2.比例的项：在比例式a cb d =（::a bcd =）中，a d ，称为比例外项，b c ，称为比例内项，d 叫做a b c ，，的第四比例项．三条线段a bb c=（2b ac =）中，b 叫做a 和c 的比例中项．3.黄金分割：如图，若线段AB 上一点C 把线段AB 分成两条线段AC 和BC （AC BC >），且使AC 是AB 和BC 的比例中项（即2AC AB BC =⋅）则称线段AB 被点C 黄金分割，点C 叫线段AB 的黄金分割点，其中510.618AC AB AB -=≈，350.382BC AB AB -=≈，AC 与AB 的比叫做黄金比．三点剖析一．考点：比例与成比例线段二．重难点：比例的性质三．易错点：注意等比定理在运用时的时候一定要对分母为0或不为0进行讨论．比例的基本性质例题1、已知23a b=（0ab≠），下列比例式成立的是（）A.32ab= B.32a b= C.23ab= D.32ba=【答案】B【解析】本题考查比例的基本性质，内项积等于外项积。

知识图谱智慧树知到课后章节答案2023年下浙江大学浙江大学第一章测试1.知识图谱可以看作是一种__的知识表示方法，相比于文本更易于被机器查询和处理，因而在搜索引擎、智能问答、大数据分析等领域被广泛应用。

（）答案:结构化2.利用知识图谱增强User 和 Item 的特征表示，有利于挖掘更深层次的用户兴趣，关系多样性也有利于实现更加个性化的推荐，丰富的语义描述还可以增强推荐结果的可解释性。

这句话描述的是知识图谱在__中的应用（）答案:推荐系统3.知识图谱的技术内涵包括（）答案:基于图的知识表示;图数据存储与查询;知识图谱推理;知识图谱融合4.知识图谱的垂直领域应用包括（）医疗健康;金融;农业;政府5.语言与知识的向量化表示，以及利用神经网络实现语言与知识的处理是重要的人工智能技术发展趋势。

（）答案:对第二章测试1.什么是知识表示？（）答案:用易于计算机处理的方式来描述人脑的知识2.以下哪个不是产生式系统的优点？（）答案:高效性3.RDF包含以下哪些元素（）。

答案:主语;宾语4.TransE模型对于以下哪种关系的处理能力不够强（）答案:多对多关系;一对多关系;多对一关系5.知识的向量表示有利于刻画那些明确非隐含的知识。

（）答案:错第三章测试1.哪种数据库更易于扩展和处理复杂关联表达（）。

答案:图数据库2.下面关于RDF图存储和属性图存储描述正确的是（）。

答案:RDF存储一般支持推理，属性图存储通常具有更好的图分析性能优势3.知识图谱的众多存储方案中，属性表存储克服了三元组表的自连接问题，同时解决了水平表中列数过多的问题。

（）答案:对4.NoSQL数据库善于处理关联关系。

（）答案:错5.基于关系型数据库存储方案中说法正确的有（）。

答案:水平表和属性表存储都存在无法表示一对多的联系或多值属性的问题;六重索引需要花费6倍的存储空间开销和数据更新维护代价第四章测试1.“26日下午，一架叙利亚空军L-39教练机在哈马省被HTS使用的肩携式防空导弹击落”这段文本中：时间实体“26号下午”，机构实体“叙利亚空军”、“HTS”，地点实体“哈马省”武器实体“L-39教练机”、“肩携式防空导弹”。

基于知识图谱的知识管理系统设计与实现第1章前言知识管理是一个广泛应用的领域，它可以帮助组织有效地利用和分享知识。

在现代企业中，知识管理被认为是提高组织竞争力的关键因素之一。

然而，随着数据量的快速增长，如何有效地管理和利用大量的知识变得越来越困难。

本文提出了一种基于知识图谱的知识管理系统，旨在提高知识管理的效率和准确性。

第2章知识图谱的基础知识图谱是一种用于表示和管理知识的语义网络。

它将知识组织为节点和边的集合，每个节点代表一个实体，每条边代表不同实体之间的关系。

知识图谱可以通过自动化技术从结构化和非结构化数据中提取实体和关系，然后将它们组织为一个具有语义理解能力的网络。

知识图谱不仅能够帮助用户快速找到所需的信息，还能够提高知识管理的准确性和效率。

第3章知识管理系统的设计知识图谱无疑是一个非常强大的工具，但想要更好地利用它，我们需要一个成熟的知识管理系统。

以下是一个基于知识图谱的知识管理系统的设计：3.1 数据收集和处理在知识管理系统中，最重要的一步是数据收集和处理。

这里的数据可以来自不同的来源，包括企业内部的数据库、文档、电子邮件等，也可以来自外部的开放数据源。

在收集数据之后，需要对数据进行处理和清洗，以消除重复和不必要的信息，同时识别出实体和关系。

这些实体和关系将作为知识图谱的构建材料。

3.2 知识图谱的构建知识图谱的构建是一项复杂的工作，需要使用一系列算法和技术来提取实体和关系，同时识别出它们之间的语义关系。

这可以通过自然语言处理、机器学习和数据挖掘等技术来实现。

知识图谱构建过程的重点是要保证实体和关系的正确性和准确性。

3.3 知识管理平台的设计基于知识图谱的知识管理系统需要一个稳定和高效的平台来管理和展示图谱数据。

平台应该具有以下特点：- 可以存储和处理大量的数据，同时支持高性能和低延迟的查询。

- 提供用户友好的界面，方便用户管理和查询知识。

- 支持多种查询方式，包括文本查询、语义查询和关系查询等。

基于知识图谱的领域知识建模与应用研究第一章引言随着信息量的不断增长和知识产生的速度加快，人们面临着巨大的知识获取和理解的挑战。

为了有效地组织和利用这些知识，学术界和工业界开始探索知识图谱的建模与应用。

知识图谱作为一种具有高可扩展性和结构化特征的知识表示方法，被广泛应用于领域知识的建模和应用研究。

第二章知识图谱概述2.1 知识图谱的定义知识图谱是一种基于图结构的知识表示模型，它通过节点和边表示实体和实体之间的关系。

知识图谱可以帮助人们理解复杂的知识关系网络，并从中提取具有实际应用价值的知识。

2.2 知识图谱的构建方法知识图谱的构建包括知识抽取、实体识别和关系抽取等过程。

知识抽取可以从结构化和非结构化数据中提取有用的知识。

实体识别是识别文本中的实体，例如人物、机构、地点等。

关系抽取是识别实体之间的关系，如母子关系、工作关系等。

第三章领域知识建模3.1 领域知识的获取领域知识的获取可以通过领域专家的知识抽取、文献分析和社交网络分析等方式进行。

领域专家可以提供领域知识的重要信息。

文献分析可以通过分析大量相关文献来获取领域知识。

社交网络分析可以通过分析社交媒体等网络平台上的信息来获取领域知识。

3.2 领域知识的表示领域知识的表示可以使用知识图谱来组织和表示。

通过将领域知识抽取出的实体和关系表示为图结构，可以更直观地展示领域知识之间的关系。

同时，可以利用图算法对领域知识进行分析和挖掘。

第四章知识图谱应用研究4.1 智能问答系统基于知识图谱的智能问答系统可以通过构建关键概念、实体和关系的知识图谱，提供更准确、全面的问题回答。

通过结合自然语言处理和知识图谱技术，可以实现从大规模知识库中获取准确答案的能力。

4.2 智能推荐系统利用知识图谱技术，智能推荐系统可以通过对用户兴趣和商品属性的建模与匹配，提供个性化的推荐服务。

知识图谱可以更准确地理解用户的需求，并为用户提供更精准的推荐结果。

第五章研究挑战与展望虽然基于知识图谱的领域知识建模与应用已经取得了一些进展，但仍然存在一些挑战。

基于知识图谱的智能电商推荐系统设计与实现第一章：引言电子商务已经成为当今社会的一种必要形式。

随着互联网技术的不断发展和普及，越来越多的人选择在电子商务平台上购物。

虽然电子商务平台为消费者和厂商带来了便利和机会，但是随着市场规模的不断扩大，竞争日益激烈，如何在众多产品和商家中找到适合自己的产品和商家变得越来越困难。

在这种情况下，智能推荐系统应运而生。

智能推荐系统基于用户的历史记录和行为，利用推荐算法来预测用户的兴趣和需求，为用户提供个性化的推荐服务。

基于知识图谱的智能推荐系统能够更好地理解用户的兴趣和需求，帮助用户更快地找到满足他们需求的产品和商家。

本文将介绍基于知识图谱的智能电商推荐系统的设计和实现。

首先，我们将探讨知识图谱和智能推荐系统的基本概念。

然后，我们将介绍如何将知识图谱和智能推荐系统相结合，提供更为准确和个性化的推荐服务。

最后，我们将给出系统的实现细节和性能分析。

第二章：知识图谱与智能推荐系统的基本概念2.1 知识图谱知识图谱是一种结构化、语义化的知识表示形式，它通过将知识结构化地组织成一个图形网络，使得计算机可以理解和处理知识。

知识图谱由多个节点和边组成，节点表示实体或概念，边表示节点之间的关系。

2.2 智能推荐系统智能推荐系统是一种利用推荐算法来预测用户兴趣和需求，并提供个性化推荐服务的系统。

传统的推荐算法包括基于内容的推荐、协同过滤推荐等。

第三章：基于知识图谱的智能电商推荐系统的设计3.1 总体设计基于知识图谱的智能电商推荐系统主要包括用户管理模块、知识图谱构建模块、推荐模块、反馈模块和可视化模块。

用户管理模块主要处理用户的注册、登录、个人信息管理等功能。

知识图谱构建模块负责从不同来源获取数据，构建知识图谱。

推荐模块根据用户的个人信息和历史行为，基于知识图谱推荐适合的产品和商家。

反馈模块用于处理用户的反馈和投诉。

可视化模块使用户可以更直观地了解系统的运作。

3.2 知识图谱构建模块知识图谱构建模块主要包括数据采集，数据预处理，实体链接，关系抽取等步骤。

知识图谱⽂献综述（第四章实体关系学习）1. 任务定义、⽬标和研究意义 关系定义为两个或多个实体之间的某种联系，实体关系学习就是⾃动从⽂本中检测和识别出实体之间具有的某种语义关系，也称为关系抽取。

关系抽取的输出通常是⼀个三元组(实体 1，关系，实体 2)。

例如，句⼦“北京是中国的⾸都、政治中⼼和⽂化中⼼”中表述的关系可以表⽰为（中国，⾸都，北京），（中国，政治中⼼，北京）和（中国，⽂化中⼼，北京）。

关系抽取是知识图谱构建和信息抽取中的⼀个关键环节，具有重要的理论意义和⼴阔的应⽤前景，为多种应⽤提供重要的⽀持，主要表现在： （1）⼤规模知识图谱的⾃动构建。

很多互联⽹应⽤都需要知识图谱的⽀撑，这个知识图谱不仅包含 WordNet、HowNet 等常识知识图谱中的通⽤语义知识，⽽且包含百科全书、领域知识图谱中的领域语义知识。

如果能把多源异构知识集成为⼀个⼤的知识图谱，将可能提⾼很多互联⽹应⽤系统的性能，并开创语义⽹时代的很多应⽤。

现有的知识图谱如 WordNet、HowNet 和 CYC 等⼤多数依靠专家⼈⼯编撰。

随着互联⽹的发展，知识呈爆炸式增长，⼈⼯构建知识图谱特别是构建领域知识图谱时遇到了很⼤困难，不仅费时费⼒，⽽且存在知识覆盖率低、数据稀疏和更新缓慢等问题。

利⽤关系抽取技术，知识图谱可以根据结构化的抽取结果⾃动⽣成。

典型的例⼦有：Freebase、Yago 和 BDpedia。

（2）为其它信息获取技术提供⽀持。

1. 对信息检索提供⽀持：可以对复杂的查询进⾏关联搜索和推理，提供智能检索结果。

例如，对于“⾝⾼ 170 以上的中国射⼿座明星”，有了关系抽取技术的⽀持，通过知识图谱构建，就可以通过推理的⽅法获得结果。

图 1 展⽰了百度搜索引擎对“⾝⾼ 170 以上的中国射⼿座明星”查询返回的结果，这个结果的背后就受到⼤规模知识图谱的⽀撑。

2. 对问答系统提供⽀持：在问答中，关键步骤是建设⼀个领域⽆关的问答类型体系并找出与问答类型体系中每个问答类型相对应的答案模式，这就需要关系抽取技术的⽀持。

在线教育平台的知识图谱研究与开发第一章：引言随着互联网技术的发展和应用，教育领域也逐渐进入了线上教育时代，传统教育与在线教育形成并存之势。

而在线教育平台具有时间、空间上的优势，被广泛应用于各级各类教育，为学生提供更加灵活、个性化的学习环境。

知识图谱技术是人工智能研究的热点之一，对于在线教育平台的知识表示与推荐等方面具有重要意义。

因此，本文将介绍在线教育平台的知识图谱研究与开发，旨在提高在线教育的效率与质量。

第二章：在线教育平台的知识图谱技术综述2.1 知识图谱技术概述知识图谱是一种结构化的语义网络，用于表示实体之间的关系和属性等信息，是人工智能发展中的新技术之一。

知识图谱不仅可以表示事物之间的联系，还可以将知识集成到一个统一的框架中，相互关联形成完整的知识系统。

知识图谱技术可以为在线教育平台提供更精确、高效、个性化的推荐和服务。

2.2 知识图谱在在线教育中的应用在线教育平台的知识图谱技术应用主要包括以下方面：（1）知识表示：将在线教育平台中的各类知识建立相应的知识图谱，从而实现知识的结构化表示和组织。

（2）个性化推荐：基于用户需求和兴趣数据，利用知识图谱技术为用户推荐适合的课程和资源。

（3）智能评估：依托知识图谱技术，可以对学生学习过程中的表现和成绩进行分析和评估，并为学生提供针对性的学习建议和辅导。

（4）智慧教学：知识图谱技术可以为教师提供更多学生学习数据和反馈信息，帮助教师识别和解决学生的学习问题，提高教学质量。

第三章：在线教育平台知识图谱技术开发与实现3.1 知识图谱的数据采集知识图谱中的知识基础来自于互联网上的各种数据资源。

在线教育平台应采集和整理与学科有关的课程、资源、试题、问题解答等数据，并对其进行标注，整理为符合知识图谱结构的数据格式。

3.2 知识图谱的构建将采集到的各类数据按照知识图谱结构进行转换，建立节点和边的关系，形成知识图谱。

需要对知识图谱中的节点和边进行标注，以便于后期应用和管理。

第01讲_变量之间的关系知识图谱变量之间的关系（北师版）知识精讲变量在一个变化过程中，我们称数值发生变化的量为变量常量在一个变化过程中，有些量的数值是始终不变的，我们称它们为常量关系一般地，在一个变化过程中，如果有两个变量x与y，并且y随着x的变化而变化，x是自变量，y是因变量二．变量关系的三种表示方法表格法；关系式法；图像法．步骤列表表中给出一些自变量的值及其对应的因变量的值描点在直角坐标系中，以自变量的值为横坐标，因变量为纵坐标，描出表格中数值对应的各点连线按照横坐标由小道大的顺序把所描出的各点用平滑曲线连接起来注意事项1．表示两个变量的对应关系的点有无数个．但是实际上我们只能描出其中有限个点，同时想象出其他点的位置2．用实心点表示在曲线的点，用空心圈表示不在曲线的点四．易错点1．确定自变量的取值范围时，不仅要考虑函数关系式有意义，而且还要注意问题的实际意义．2．解决图象有关的问题，一定要注意理解横、纵坐标所表示的实际含义，然后根据图象求出函数解析式来解题．3．不能认为式子中出现的字母都是变量，如π不是变量而是常量．三点剖析一．考点：1．用表格表示的变量间关系； 2．用关系式表示的变量间关系； 3．用图象表示的变量间关系．二．重难点：用图象表示的变量之间的关系三．易错点：1．确定自变量的取值范围时，不仅要考虑函数关系式有意义，而且还要注意问题的实际意义．2．解决图象有关的问题，一定要注意理解横、纵坐标所表示的实际含义，然后根据图象求出函数解析式来解题．用表格表示的变量间关系例题1、 弹簧挂上物体后会伸长，测得一弹簧的长度y （cm ）与所挂的物体的质量x （kg ）间有下面的关系： 下列说法不正确的是（ ）A.x 与y 都是变量，且x 是自变量，y 是因变量B.所挂物体质量为4kg 时，弹簧长度为12cmC.弹簧不挂重物时的长度为0cmD.物体质量每增加1kg ，弹簧长度y 增加0.5cm 【答案】 C【解析】 根据给出的表格中数据分析，可以确定自变量和因变量以及弹簧伸长的长度，得到答案．例题2、 已知某易拉罐厂设计一种易拉罐，在设计过程中发现符合要求的易拉罐的底面半径与铝用量有如下关系：（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？ （2）当易拉罐底面半径为2.4cm 时，易拉罐需要的用铝量是多少？（3）根据表格中的数据，你认为易拉罐的底面半径为多少时比较适宜？说说你的理由． （4）粗略说一说易拉罐底面半径对所需铝质量的影响．【答案】 （1）易拉罐底面半径和用铝量的关系，易拉罐底面半径为自变量，用铝量为因变量； （2）当底面半径为2.4cm 时，易拉罐的用铝量为356.cm ．（3）易拉罐底面半径为2.8cm 时比较合适，因为此时用铝较少，成本低．（4）当易拉罐底面半径在1.6～2.8cm 变化时，用铝量随半径的增大而减小，当易拉罐底面半径在2.8～4.0cm 间变化时，用铝量随半径的增大而增大．【解析】 本题考查函数的自变量与函数变量，根据表格理解：随底面半径的增大，用铝量的变化情况是关键． 例题3、 某校组织学生到距学校6km 的光明科技馆参观，准备乘出租车去科技馆，出租车的收费标准如表：则收费y （元）与出租车行驶里程数x （km ）（x ≥3）之间的关系式为（ ）x 0 1 2 3 4 5y 10 10.5 11 11.5 12 12.5底面 半径 1.6 2.0 2.4 2.8 3.2 3.6 4.0 用铝量 6.96.05.65.55.76.06.5里程数收费/元 3km 以下（含3km ） 8.00 3km 以上每增加1km1.80A.y=8xB.y=1.8xC.y=8+1.8xD.y=2.6+1.8x【答案】 D【解析】 由题意得，所付车费为：y=1.8（x ﹣3）+8=1.8x+2.6（x ≥3）． 故选：D ．随练1、 心理学家发现，学生对概念的接受能力y 与提出概念所用的时间x （单位：分）之间有如下关系：（其中030x ≤≤）（1）上表中反映了哪两个变量之间的关系？（2）当提出概念所用时间是10分钟时，学生的接受能力是多少？（3）根据表格中的数据，你认为提出概念几分钟后，学生的接受能力最强；（4）从表中可知，当时间x 在什么范围内，学生的接受能力逐步增强？当时间x 在什么范围内，学生的接受能力逐步降低？【答案】 见解析【解析】 （1）提出概念所用的时间x 和对概念接受能力y 两个变量； （2）当10x =时，59y =，所以时间是10分钟时，学生的接受能力是59；（3）当13x =时，y 的值最大是59.9，所以提出概念13分钟时，学生的接受能力最强； （4）由表中数据可知：当213x <<时，y 值逐渐增大，学生的接受能力逐步增强；当1320x <<时，y 值逐渐减下，学生的接受能力逐步降低．用关系式表示的变量间关系例题1、 写出下列各问题中的关系式，指出其中的常量、自变量、因变量及自变量取值范围． （1）直角三角形中一锐角的度数y 与另一锐角的度数x 之间的函数关系．（2）如果水的流速量是a m/min (一个定量)，那么每分钟的进水量3Q()m 与所选择的水管直径D (m )之间的函数关系． 【答案】 （1）90y x =-，90是常量，x 是自变量，y 是因变量，自变量x 的取值范围是090x <<；（2）24aD Q π=，常量为4aπ，自变量为D ，Q 为因变量，自变量0D >【解析】 （1）直角三角形两锐角互余，所以90y x =-，其中90是常量，x 是自变量，y 是因变量，自变量x 的取值范围是090x <<；（2）由水管直径为D 可知，水管的截面积为24D π，所以24aD Q π=，其中常量为4aπ，自变量为D ，Q 为因变量，自变量0D >；例题2、 等腰三角形的周长为16cm ，底边长为x cm ，腰长为y cm ，则x 与y 之间的关系式为_________． 【答案】 y=8﹣12x （0＜x ＜8） 【解析】 ∵等腰三角形的周长为16cm ，底边长为x cm ，腰长为y cm ． ∴x+2y=16， ∴y=8﹣12x （0＜x ＜8）． 例题3、 等腰三角形的周长为16cm ，底边长为x cm ，腰长为y cm ，则x 与y 之间的关系式为 ．【答案】 y=8﹣12x （0＜x ＜8）．【解析】 ∵等腰三角形的周长为16cm ，底边长为x cm ，腰长为y cm ．提出概念所用时间（x ） 257101213141720对概念的接受能力（y ）47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55∴x+2y=16，∴y=8﹣12x（0＜x＜8）．故答案为：y=8﹣12x（0＜x＜8）．随练1、等腰三角形的周长为30，则腰长y关于底边长x的函数关系式为__________，其中自变量x的取值范围是__________．【答案】1152y x=-+；015x<<【解析】230y x+=，整理得，1152y x=-+，根据三角形三边关系定理，02x y<<，∴102152x x⎛⎫<<-+⎪⎝⎭，∴015x<<．随练2、以直角三角形中的一个锐角的度数为自变量x，另一个锐角的度数y为因变量，则它们的关系式是．【答案】y=90°﹣x．【解析】根据题意得y=90°﹣x．故答案为y=90°﹣x．用图象表示的变量间关系例题1、小华同学利用假期时间乘坐一大巴去看望在外打工的妈妈，出发时，大巴的油箱装满了油，匀速行驶一段时间后，油箱内的汽油恰剩一半时又加满了油，接着按原速度行驶，到目的地时油箱中还剩有13箱汽油，设油箱中所剩汽油量为V升，时间为t（分钟），则V与t的大致图象是（）A.AB.BC.CD.D【答案】D【解析】A、从图象可知最后纵坐标为0，即油箱是空的，与题意不符，故本选项错误；B、图象没有显示油箱内的汽油恰剩一半时又加满了油的过程，与题意不符，故本选项错误；C、图象显示油箱的油用完以后又加满，与题意不符，故本选项错误；D、当t为0时，大巴油箱是满的，然后匀速减少至一半，又加满，到目的地是油箱中还剩有13箱汽油，故本选项正确．故选D．例题2、如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（）A.乙前4秒行驶的路程为48米B.在0到8秒内甲的速度每秒增加4米/秒C.两车到第3秒时行驶的路程相同D.在4到8秒内甲的速度都大于乙的速度【答案】C【解析】A、根据图象可得，乙前4秒的速度不变，为12米/秒，则行驶的路程为12×4=48米，故A正确；B、根据图象得：在0到8秒内甲的速度是一条过原点的直线，即甲的速度从0均匀增加到32米/秒，则每秒增加32 8=4米秒/，故B正确；C 、由于甲的图象是过原点的直线，斜率为4，所以可得v=4t （v 、t 分别表示速度、时间），将v=12m/s 代入v=4t 得t=3s ，则t=3s 前，甲的速度小于乙的速度，所以两车到第3秒时行驶的路程不相等，故C 错误；D 、在4至8秒内甲的速度图象一直在乙的上方，所以甲的速度都大于乙的速度，故D 正确．随练1、 一个装有进水管和出水管的容器，从某一时刻起只打开进水管进水，经过一段时间，再打开出水管放水，至12分钟时，关停进水管．在打开进水管到关停进水管这段时间内，容器内的水量y （单位：升）与时间x （单位：分钟）之间的函数关系如图所示，关停进水管后，经过_____分钟，容器中的水恰好放完．【答案】 8【解析】 由04-分钟的函数图象可知进水管的速度，根据412-分钟的函数图象求出水管的速度，再求关停进水管后，出水经过的时间．进水管的速度为：2045÷=（升/分），出水管的速度为：()()53020124 3.75--÷-=（升/分），∴关停进水管后，出水经过的时间为：30 3.758÷=分钟．随练2、 上周周末放学，小华的妈妈来学校门口接他回家，小华离开教室后不远便发现把文具盒遗忘在了教室里，于是以相同的速度折返回去拿，到了教室后碰到班主任，并与班主任交流了一下周末计划才离开，为了不让妈妈久等，小华快步跑到学校门口，则小华离学校门口的距离y 与时间t 之间的函数关系的大致图象是（ ）A. B. C. D.【答案】 B【解析】 根据题意得，函数图象是距离先变短，再变长，在教室内没变化，最后迅速变短，B 符合题意随练3、 在20km 越野赛中，甲乙两选手的行程y （单位：km ）随时间x （单位：h ）变化的图象如图所示，根据图中提供的信息，有下列说法：①两人相遇前，甲的速度小于乙的速度； ②出发后1小时，两人行程均为10km ； ③出发后1.5小时，甲的行程比乙多3km ； ④甲比乙先到达终点． 其中正确的有_______个．【答案】 1【解析】 在两人出发后0.5小时之前，甲的速度小于乙的速度，0.5小时到1小时之间，甲的速度大于乙的速度，故①错误由图可得，两人在1小时时相遇，行程均为10km ，故②正确；甲的图象的解析式为y=10x ，乙AB 段图象的解析式为y=4x+6，因此出发1.5小时后，乙的路程为15千米，甲的路程为12千米，甲的行程比乙少3千米，故③错误；乙到达终点所用的时间较少，因此乙比甲先到达终点，故④错误．拓展1、 如图所示，某计算装置有一个数据输入口A 和一个运算结果输入口B ，下表给出的是小红输入的数字及所得的运算结果（1）若小红输入的数为x ，输出的结果为y ，你能用x 表示y 么？请写出来．（不需要写出x 的取值范围）（2）若输出结果为8，求小红输入的数字 【答案】 （1）1y x =-（2）81【解析】 （1）由表中数据可观察到，每个B 中数据都是在A 中数据开方后减一所得，101-=-，011=-，141=-，∴可得到函数1y x =-．（2）当8y =时，()211y x x y =-⇒=+，∴2981x ==．2、 弹簧挂上物体后会伸长，测得一弹簧的长度()y cm 与所挂的物体的质量()x kg 间有下面的关系：下列说法不正确的是（ ）A.x 与y 都是变量，且x 是自变量，y 是因变量B.所挂物体质量为4kg 时，弹簧长度为12cmC.弹簧不挂重物时的长度为0cmD.物体质量每增加1kg ，弹簧长度y 增加0.5cm 【答案】 C【解析】 弹簧不挂重物时的长度为10cm3、 在某次实验中，测得两个变量m 和v 之间的4组对应数据如下表：则m 与v 之间的关系最接近于下列各关系式中的（ ）A.22v m =-B.21v m =-C.33v m =-D.1v m =+【答案】 B【解析】 分别代入当4m =时，算出v 即可．4、 购买单价为每支1.2元的铅笔，总金额y （元）与铅笔数n （支）的关系式可表示为y =__________，其中，__________是常量，__________是变量． 【答案】 1.2n ，单价，铅笔数【解析】 总金额等于每支铅笔的价格乘以铅笔的支数，故 1.2y n =，铅笔的单价是常量，铅笔数是变量． 5、 乘坐某种出租汽车，当行驶路程小于或等于3千米时，乘车费用都是10元（即起步价10元），当行驶路程大于3千米时，超过3千米的部分每千米收费2元，若一次乘坐这种出租车行驶4千米，则应付车费__________元；若一次乘坐这种出租车付费20元，则乘车路程是__________千米． 【答案】 12,8【解析】 本题考查函数的应用。

知识图谱在智能推荐算法中的应用分析第一章知识图谱概述知识图谱（Knowledge Graph）是一种基于语义网络的知识表示模型，它将知识结构化、标准化、语义化，形成了一个大规模的知识库。

知识图谱通过将实体、属性和关系抽象成节点、边和标签，描述实体之间的关系，进而实现知识的共享和应用。

知识图谱是人工智能、机器学习和自然语言处理的重要技术基础，在文本分析、信息检索、智能推荐等领域得到了广泛的应用。

第二章知识图谱与智能推荐智能推荐系统是一种基于用户历史行为、兴趣偏好和个性化需求等信息，通过算法模型实现对用户进行商品、服务等推荐的一种技术。

知识图谱作为一种知识表示模型，有着在智能推荐系统中发挥重要作用的潜力。

通过将用户自身特征、商品特征、其他因素等抽象为实体节点，并通过相应关系连接起来，形成一个复杂的图结构，实现推荐结果的智能化生成。

第三章知识图谱在推荐系统中的应用3.1 用户画像通过将用户的历史行为、个人信息、社交网络等信息进行抽象和标注，形成一个用户画像或者多个用户画像，为推荐模型提供个性化推荐支持。

3.2 商品描述与分类通过对商品信息进行分类、属性抽取、关系分析等技术处理，将商品特征形成一个结构化的知识图谱，为推荐系统提供更为细致和准确的商品信息。

3.3 推荐算法与模型结合知识图谱的特点，基于图模型和知识表示学习技术进行推荐算法的研究，可以通过将用户特征、商品特征和其他因素抽象为实体节点，通过节点间的连接关系所带的语义信息进行推荐结果的生成。

此外，针对不同的应用场景，还可以基于知识图谱提取出的关系进行特定领域、特定对象等的推荐。

第四章知识图谱在电子商务领域的应用4.1 个性化推荐通过分析用户的历史购买行为、浏览记录、搜索关键词以及其他因素等，在知识图谱中建立用户画像，并结合商品信息和购买环境等因素进行个性化推荐，为用户提供更为准确和便捷的购物体验。

4.2 智能客服基于知识图谱为电子商务领域提供的商品信息、支付流程、物流信息等知识，为用户提供智能化的客户服务支持，包括自动回答、在线客服、投诉处理等功能。

面向跨媒体的知识图谱建设技术研究第一章：引言知识图谱是自然语言理解、语义计算和人工智能等前沿技术众多应用领域中的核心。

近年来，随着多媒体技术的飞速发展，跨媒体知识图谱建设成为了新的研究热点。

本文旨在从数据来源、跨媒体数据融合和知识表示等角度对面向跨媒体的知识图谱建设技术进行探讨。

第二章：数据来源面向跨媒体的知识图谱建设需要从多种数据源中获取数据。

这些数据源包括结构化数据、半结构化数据和非结构化数据等。

其中，结构化数据包括关系型数据库、XML文档等，半结构化数据包括HTML网页、JSON数据等，非结构化数据包括图像、音频、视频等。

在获取数据时，需要考虑到数据的完整性、准确性和可用性等方面的问题。

数据的完整性指的是数据中是否包含了所有相关信息，数据的准确性指的是数据中的信息是否准确无误，可用性指的是数据是否容易被访问和利用。

第三章：跨媒体数据融合面向跨媒体的知识图谱建设需要将来自不同数据源的数据进行融合。

跨媒体数据融合的挑战在于不同类型的数据之间存在差异，需要考虑到数据的异构性和数据的不确定性等问题。

面向跨媒体的数据融合主要包括以下三个方面的问题：1.数据语义的映射数据融合的一个关键问题是如何将来自不同数据源的数据进行语义映射，使得不同数据源之间的语义能够协同工作。

主要解决方法有：基于本体的方法、基于统计的方法和基于机器学习的方法等。

2.数据的冲突和重复不同数据源之间可能存在数据的重复和冲突问题。

解决这个问题的方法包括：基于规则的方法、基于统计的方法和基于机器学习的方法等。

3.数据的不确定性不同数据源之间存在数据的不确定性问题。

解决这个问题的方法包括：基于不确定性理论的方法、基于概率模型的方法和基于贝叶斯模型的方法等。

第四章：知识表示知识表示是面向跨媒体的知识图谱建设过程中的一个关键问题。

知识表示指的是将事实和概念变成计算机可以理解的形式，以便计算机可以处理和利用。

知识表示技术主要包括以下几种方法：1.本体表示法本体表示法是将知识表示为一个本体类别层次结构，包含有关概念的信息和关系。

基于搜索引擎的知识图谱构建技术研究第一章：绪论随着互联网的快速发展，人们的信息获取需求日益增加。

然而，大量的信息使得人们很难找到自己需要的内容。

搜索引擎因此应运而生，成为人们日常必不可少的信息获取工具。

传统的搜索引擎只能提供文本搜索，而人们对于信息的需求已经从单纯的文本需求转变为更加复杂的知识需求。

因此，搜索引擎需要跨越文本搜索，实现对知识的搜索。

基于搜索引擎的知识图谱构建技术因此应运而生。

第二章：知识图谱的基础概念知识图谱旨在将知识表示为一张图，是一种将知识互联、可视化展示的技术。

在知识图谱中可以看到多个节点之间以各种关系连成网络，每个节点及关系都代表某项知识。

知识图谱的基础是实体、属性和关系。

实体是知识图谱中的节点，其可以表示现实世界中的各种事物。

属性是指面向实体的某个特定方面的描述。

关系则是实体和实体之间的连接，实体与关系共同构成了一个完整的知识图谱。

第三章：知识图谱构建技术知识图谱构建需要经过三个关键步骤：知识抽取、知识存储和知识推理。

知识抽取是从海量数据中提取出真正有用的信息，包括实体、属性和关系。

而知识存储则是将抽取出的信息以一定规则进行存储，使其能够在知识图谱中展示。

知识推理是在知识图谱中进行信息的推理和计算，从而得到更高级别的知识。

第四章：搜索引擎的知识图谱搜索引擎的知识图谱可以更好地为用户提供知识服务。

搜索引擎的知识图谱利用搜索引擎的强大检索功能，将抽取出的信息进行关联，并且将关键的知识关系网络化，使得用户可以根据自己的需要快速定位信息。

同时，搜索引擎基于知识图谱的工作方式，可以更好地应对信息搜索的各种问题。

第五章：知识图谱构建技术的应用知识图谱的构建技术能够广泛应用于各种领域。

比如，知识图谱可以应用于智能客服，将客户的提问进行知识抽取和关联，从而更快地解决客户的疑问。

知识图谱还可以用于智能家居，将不同设备和应用关系进行关联，形成家庭智能网络。

同时，知识图谱也可以用于智能医疗，将医疗领域的知识关系进行关联，更快更准确地对疾病进行诊断和治疗。