简支梁计算示例

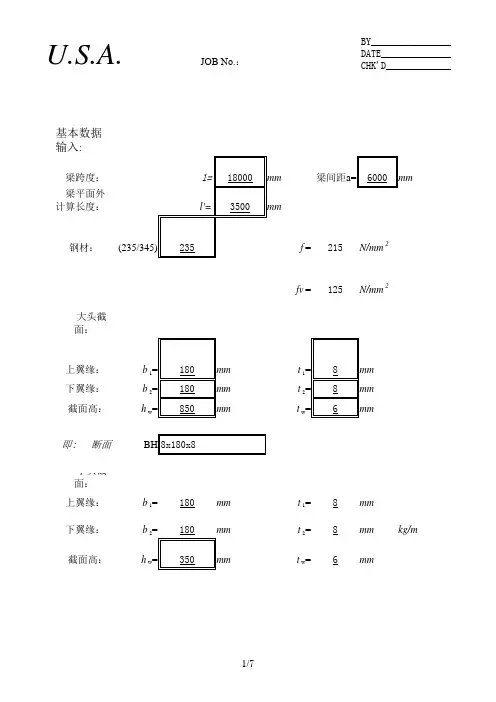
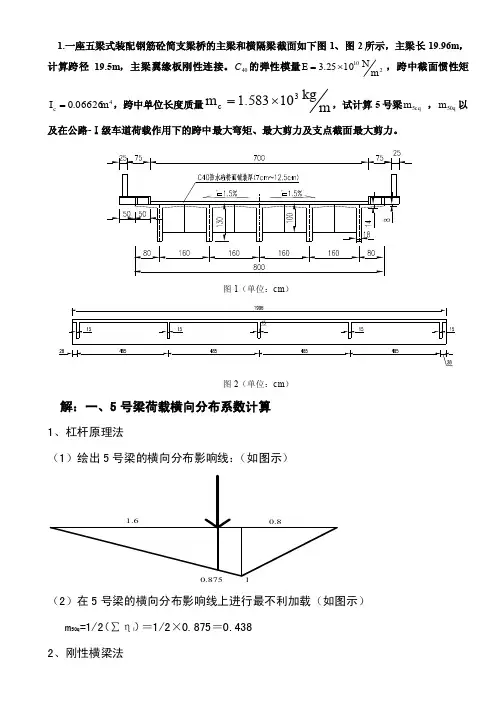
1.一座五梁式装配钢筋砼简支梁桥的主梁和横隔梁截面如下图1、图2所示，主梁长19.96m ，计算跨径19.5m ，主梁翼缘板刚性连接。

40C 的弹性模量210m N105.23E ⨯=，跨中截面惯性矩4c m 06626.0I =，跨中单位长度质量m kg 1083.51m 3c ⨯=，试计算5号梁5cq m ，50q m 以及在公路-Ⅰ级车道荷载作用下的跨中最大弯矩、最大剪力及支点截面最大剪力。

图1（单位：cm ）图2（单位：cm ）解：一、5号梁荷载横向分布系数计算1、杠杆原理法（1）绘出5号梁的横向分布影响线：（如图示）10.8751.60.8（2）在5号梁的横向分布影响线上进行最不利加载（如图示）m 50q =1/2(∑ηi )＝1/2×0.875＝0.4382、刚性横梁法(1)求5号梁的横向分布影响线：(以桥跨中心为坐标原点建立坐标系：如图示)∑a i 2=a 12+ a 22 +a 32 +a 42+ a 52=2×（3.22+1.62）=25.6η51= 1/n-a 5×a 1/∑a i 2=1/5-3.2×3.2/25.6=-0.2η55= 1/n+a 3×a 7/∑a i 2=1/5+3.2×3.2/25.6=0.6绘出5号梁的横向分布影响线(2)在5号梁的横向分布影响线上进行最不利加载：绘出加载图0.875η1=(480-20)/480*0.6=0.575η2=(480-200)/480*0.6=0.35η3=(480-330)/480*0.6=0.1875η4=-30/480*0.6=-0.0375 ?m 5cq =1/2(∑ηi )=1/2(0.1875+0.35+0.575)=0.556m 5cq =1/2(∑ηi )=1/2(0.1875+0.35+0.575-0.0375)=0.538 ?二．内力计算1、恒载内力)(222x l gxx gx x glM x -=⨯-⨯=)2(22x l ggx gl Q x -=-=g=1.583*103kg/m=1.583/9.8*103=16.15kN/m各计算截面的剪力和弯矩值如下表:5号梁恒载内力2、活载内力计算课程设计中要计算简支桥基频，公式为：cc m EI l f 22π=再根据计算基频选择冲击系数。

如图所示简支梁，截面尺寸 b ×h = 250×500，采用 C20 混凝土，纵向受拉钢筋采用Ⅱ级(HRB335)钢筋，箍筋用Ⅰ级(HPB235)钢筋,梁内配有纵向受拉钢筋 325，箍筋φ6@200，试确定该梁所能承受的均布荷载设计值（不包括梁自重）。

解：1、由抗弯确定得均布荷载设计值：bh A s =ρ==⨯46525014730.01267, cy f f 1αρξ===⨯⨯6.90.130001267.00.396 < ξb = 0.55，适筋,()()8.164396.05.01396.04652506.90.15.012201=⨯-⨯⨯⨯⨯⨯=-=ξξαbh f M c kN·m,28lM q ===⨯⨯234260108.164872.65 kN/m扣去梁得自重后能承担的净荷载： 5.025.0252.1-72.65 q'⨯⨯⨯==68.9 kN/m 2、由抗剪确定得均布荷载设计值：0025.17.0h snA f bh f V sv yvt +===⨯⨯⨯⨯+⨯⨯⨯4652003.221025.14652501.17.0124.056 kN ，=⨯42602.1240562= q 58.24 kN/m扣去梁得自重后能承担的净荷载： 5.025.0252.1-58.24 'q'⨯⨯⨯==54.49kN/m 最后承担的净荷载为54.49kN/m钢筋混凝土矩形截面简支梁，b ×h = 200×500，L = 4.04 m ，支座 a = 240mm ，承受均布荷载设计值 80 kN/m （包括自重），混凝土强度等级为 C20，纵向受拉钢筋采用Ⅱ级(HRB335)钢筋，箍筋用Ⅰ级(HPB235)钢筋，求箍筋和弯起钢筋的数量。

解：1、求V ： 04.4802121 V ⨯⨯==ql =161.6 kN2、验算截面尺寸：h o =h- a s = 465，hw / b < 4，3、是否按计算配箍：4652001.17.07.00⨯⨯⨯=bh f t = 71.6 kN<V ，应按计算配箍。

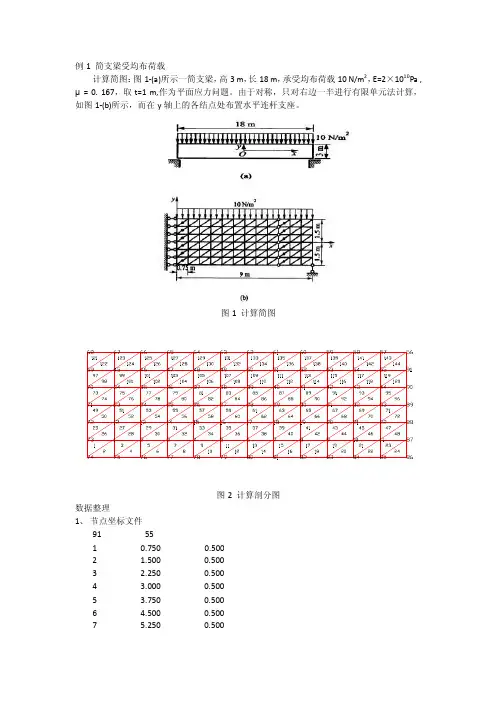
例1 简支梁受均布荷载计算简图：图1-(a)所示一简支梁，高3 m，长18 m，承受均布荷载10 N/m2，E=2×1010Pa ,μ= 0. 167，取t=1 m,作为平面应力问题。

由于对称，只对右边一半进行有限单元法计算，如图1-(b)所示，而在y轴上的各结点处布置水平连杆支座。

图1 计算简图图2 计算剖分图数据整理1、节点坐标文件91 551 0.750 0.5002 1.500 0.5003 2.250 0.5004 3.000 0.5005 3.750 0.5006 4.500 0.5007 5.250 0.5009 6.750 0.50010 7.500 0.50011 8.250 0.50012 0.750 1.00013 1.500 1.00014 2.250 1.00015 3.000 1.00016 3.750 1.00017 4.500 1.00018 5.250 1.00019 6.000 1.00020 6.750 1.00021 7.500 1.00022 8.250 1.00023 0.750 1.50024 1.500 1.50025 2.250 1.50026 3.000 1.50027 3.750 1.50028 4.500 1.50029 5.250 1.50030 6.000 1.50031 6.750 1.50032 7.500 1.50033 8.250 1.50034 0.750 2.00035 1.500 2.00036 2.250 2.00037 3.000 2.00038 3.750 2.00039 4.500 2.00040 5.250 2.00041 6.000 2.00042 6.750 2.00043 7.500 2.00044 8.250 2.00045 0.750 2.50046 1.500 2.50047 2.250 2.50048 3.000 2.50049 3.750 2.50050 4.500 2.50051 5.250 2.50053 6.750 2.50054 7.500 2.50055 8.250 2.50056 9.000 3.00057 8.250 3.00058 7.500 3.00059 6.750 3.00060 6.000 3.00061 5.250 3.00062 4.500 3.00063 3.750 3.00064 3.000 3.00065 2.250 3.00066 1.500 3.00067 0.750 3.00068 0.000 3.00069 0.000 2.50070 0.000 2.00071 0.000 1.50072 0.000 1.00073 0.000 0.50074 0.000 0.00075 0.750 0.00076 1.500 0.00077 2.250 0.00078 3.000 0.00079 3.750 0.00080 4.500 0.00081 5.250 0.00082 6.000 0.00083 6.750 0.00084 7.500 0.00085 8.250 0.00086 9.000 0.00087 9.000 0.50088 9.000 1.00089 9.000 1.50090 9.000 2.00091 9.000 2.500该文件第1行第1个数据为节点数91，第2个数据为内部节点数55。

钢筋混凝土简支梁挠度计算算例编写 王行耐某装配式钢筋混凝土T 形截面简支梁，计算跨径L=19.5m ，跨中截面尺寸b=24cm 、h=100cm 、b i =178cm 、h i =12cm ，配置HRB400钢筋(12φ32，A s =96.516cm 2)，跨中截面恒载弯矩标准值M GK =912.52kN.m ，汽车荷载弯矩标准值(包括冲击力)M Q1K =859.57kN.m ，冲击系数(1+μ)=1.19，人群荷载弯矩标准值M Q2K =85.44kN.m 。

试验算此梁跨中截面裂缝宽度。

解：荷载短期效应作用下的跨中截面挠度按下式近似计算：BMl f 2485⋅= 其中：荷载短期效应组合mkN M M M M KQ K Q GK S .59.1503 44.85)19.1/(51.8597.052.912 )1/(7.021=+⨯+=+++=μL=19.50m=19.5×105mmcr s cr s cr B B M M M M B B 02201⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=0B 为全截面抗弯刚度，B 0=0.95E c J 0，按全截面参加工作计算，取f b '=1780mm ，Es α=E S /E 0=2×105/3×104≈6.67，换算截面重心至受压缘的距离'0y =386.2mm ， 至受拉缘的距离0y =1000-386.2=613.8mm 。

换算截面惯性矩0J =5.9881×1010mm 4，对受拉边缘的弹性抵抗矩000/y J W == 5.9881×1010/613.8=9.7557×107mm 3，换算截面重心以上部分面积对重心轴的面积矩为：S 0 =240×386.22/2+(1780-240)×120×(386.2-120/2)=78179812.8mm 2取E C =3.0×104MPa ，将以上数据代入公式得B 0=0.95×104×5.9881×1010=17.0661×1014N.mm 2B cr 为开裂截面的抗弯刚度，B cr =E c J cr ，开裂截面的换算截面几何特征值，按有关公式计算求得：混凝土受压区高度x 0=247.2mm换算截面惯性矩J cr =3.5202×1010mmB cr =3.0×104×3.5202×1010=10.5607×1014N.mm开裂弯矩 0W f M tk cr γ=γ=2S 0/W 0=2×78179812.8/9.7557×107=1.6028，tk f =2.01MPa ，代入上式得：M cr =1.6028×2.01×9.7557×107=310.29×106N.mm=310.29kN.mM s =1503.59kN.m将以上数据代入公式得mmkN B B M M M M B B cr s cr s cr .10738.10 105607.10100061.1759.150329.314159.150329.314100061.17 114141422140220⨯=⨯⨯⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛⨯=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=荷载短期效应作用下跨中截面挠度为： mm B Ml f s 2.5310738.10195001059.150348548514262=⨯⨯⨯⋅=⋅= 长期挠度为：mm L mm f f s l 19.121600/195001610/2.852.536.1==>=⨯==θη应设置预拱度，预拱度值按结构自重和1/2可变作用频遇值计算的长期挠度值之和采用。

【例1】钢筋混凝土简支T形梁桥，计算各梁在结构重力及汽车荷载、人群荷载作用下的设计内力。

【设计资料】桥面净空：净一7+2× 1m；主梁跨径和全长，标准跨径：I h = 13/72,计算跨径：7 = 12. 5勿，主梁全长；L = 12. 96/77 ；设计荷载：大路T级汽车荷载，人群荷载为3. lkN/m*结构重要系数%=1.0；材料规格：主梁纵向受力主筋采纳HRB335钢筋，箍筋采纳R235钢筋，主梁采纳C35混凝土；桥面铺装层厚度为8~10cm,容重为24 kN/m3；全桥每跨采纳4根预制的钢筋混凝土T形梁，每根行车道板宽2. 20m,沿主梁纵向布置5根横隔梁；主梁及横隔梁容重为25 kN/m3；每侧的栏杆及人行道构件重量的作用力为4 kN/m；汽车荷载纵断面布置如图1所示。

28OkN 30kN240kN SSOkN图1汽车荷载纵向布置图图2桥梁横断面图【解】1、结构自重计算 （1）自重集度计算 主梁：8 = 0. 18 × 1. 1 ++（）• 20 X （2. 2 - 0. 18）× 25 = 13. 03kN / m 2边主梁横隔板：7八 CU 0∙ 12+ 0.20、 2.2 — 0.18] λ ic c oc/1o c 1 oλzv z g.y =0. 95 × × 0. 15× 5 × 2□∕12. 5 = 1. 2OAjV / mLl 2 J 2 J主梁横隔板：g ； = 2 X W2 = 2. 404N / m桥面铺装层：/ = " 0® 十 ×7× 24/4 = 3. 78AvV / m 3 2 人行道：岗=4 × 2/4 = 2kN / m 合计：15图3桥梁纵断面图图4 T 形梁横截面图边主梁自重集度：g = & +宪+ +岗=20∙OlkN / m主梁自重集度：g = & +4+8+岗=21. 2W / m（2）结构自重计算：【简支梁承受的荷载集度为g,简支梁长乙其距离左端为'的横截面上弯矩材⑺和剪力分别为：M（X）= %x- gx 嗅=詈U-*）0（X）=9.=["2X）1乙乙2【当夕=1位于第4号梁轴上（e = ¾）时，对，号主梁的总作用为:荷载位置e和梁位%位于形心轴同侧时，取正好，反之取负号。

点载荷简支梁扭矩计算公式全文共四篇示例，供读者参考第一篇示例：点载荷简支梁扭矩计算公式是工程力学领域中常用的公式之一，它用来计算简支梁在承受外部载荷作用时产生的扭矩大小。

在工程设计中，扭矩是一个非常重要的参数，能够影响梁的强度、稳定性和耐久性。

准确计算简支梁的扭矩对于工程设计和结构安全具有重要意义。

在工程实践中，简支梁扭矩的计算公式通常采用静力学的原理，结合梁的几何形状和外部载荷的作用来确定。

一般情况下，简支梁的扭矩计算公式可以表示为：M = -M0 + Px – VxM为简支梁的扭矩，单位为N·m；M0为简支梁的固定端的扭矩，单位为N·m；P为梁的外部载荷，单位为N；x为梁的距离离开固定端的距离，单位为m；V为梁的剪力，单位为N。

简支梁是一种常用的结构形式，在实际的工程设计中经常遇到。

简支梁是指在两端支承条件下的梁，通常由一根梁材或梁柱组成，用于支撑和承载外部荷载。

简支梁的设计和计算是工程设计中一个重要的环节，其中扭矩计算公式是不可或缺的一部分。

在实际的工程设计中，工程师通常会根据具体的工程要求和结构形式来选择合适的简支梁扭矩计算公式。

通过合理的计算和分析，可以有效地评估简支梁在承受外部载荷时的受力情况，为工程设计和结构安全提供重要的参考依据。

点载荷简支梁扭矩计算公式是工程设计中的重要工具，在工程实践中具有广泛的应用。

通过准确计算简支梁的扭矩，可以帮助工程师评估结构的强度和稳定性，为工程设计和结构安全提供保障。

在未来的工程实践中，我们需要不断改进和完善简支梁扭矩计算公式，以更好地满足工程设计的需要，促进工程结构的发展和进步。

第二篇示例：点载荷简支梁是工程结构设计中常见的一种构件形式，扭矩是梁在受到外力作用时内部产生的一种重要力学参数。

在设计工程结构时，计算扭矩是十分关键的，可以帮助工程师合理布局结构，确保结构的稳定性和安全性。

本文将介绍点载荷简支梁扭矩的计算公式及其相关知识。

简支梁计算例题设计任务：设计一个简支梁，已知梁的跨度L=6米，梁的截面尺寸为b×h=200×400毫米，承受均布荷载设计值q=70kN/m（包括自重），混凝土强度等级为C25，纵向受拉钢筋采用HRB400级钢筋，箍筋采用HPB300级钢筋。

1. 计算梁所受总弯矩M：M = qL²/ 8 = 70 ×6²/ 8 = 255 kN·m2. 计算梁的截面面积A：A = b ×h = 200 ×400 = 80000 mm²3. 计算梁的截面模量W：W = α×A ×fcm = 1.1 ×80000 ×30 = 2640000 N·mm4. 计算梁的抗弯承载力Mu：Mu = fcmw = 30 ×2640000 = 79200000 N·mm > M = 25500000 N·mm5. 计算梁的纵筋数量：由M/mho²+fyAs/s ≤fcd得出As ≥M/(mho²+ fy/s)，其中fy为HRB400级钢筋的抗拉强度设计值，取值为360N/mm²。

通过计算得出As≥8176mm²，选用2Φ28的钢筋，As=12568mm²。

6. 计算箍筋数量：根据构造要求，选用Φ8@200的箍筋，每米长度内布置箍筋数量为n=1×100/200+1=2个。

7. 验算裂缝宽度：根据规范要求，裂缝宽度不应超过Wmax=0.3mm。

根据M/γfW≤Wmax，其中γf为受拉或受压区纵向普通钢筋的配筋率，取值为As/(bho)，通过计算得出W≤Wmax。

8. 绘制施工图，标明梁的跨度、截面尺寸、纵向钢筋和箍筋的位置和规格。

结论：根据以上计算和验算，该简支梁的设计满足要求，可以用于实际工程中。