简支梁计算表

格式：xls
大小：37.50 KB
文档页数：7

下载文档原格式

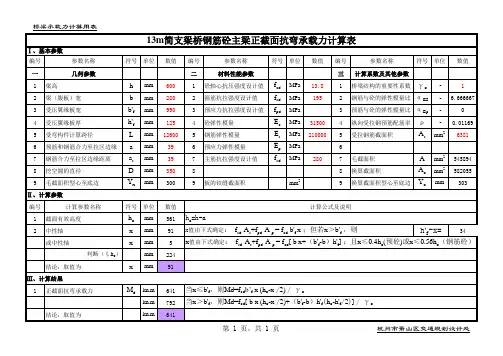
简支梁正截面抗弯承载力计算表格

4 砼弹性模量
5 钢筋弹性模量
6 预应力弹性模量
7 主筋抗拉强度设计值
8
9 板的铰缝截面积
fcd MPa 13.8 fsd MPa 195 fpd MPa Ec MPa 31500 Es MPa 210000 Ep MPa fsd MPa 280
mm2
三计算系数及其他参数
1 桥梁结构的重要性系数 γo 2 钢筋与砼的弹性模量比 αES 3 预筋与砼的弹性模量比 αEp 4 纵向受拉钢预筋配筋率 ρ
桥梁承载力计算用表
Ⅰ、基本参数
编号
参数名称
13m简支梁桥钢筋砼主梁正截面抗弯承载力计算表
符号单位数值编号
参数名称
符号单位数值编号
参数名称
符号单位数值
一
几何参数
1 梁高
2 梁（腹板）宽
3 受压翼缘板宽
4 受压翼缘板厚
5 受弯构件计算跨径
6 预筋和钢筋合力至拉区边缘
7 钢筋合力至拉区边缘距离
224
91
641 当x≤b'f，则Md=fcdb’f x (ho-x /2) / γo 792 当x＞b'f，则Md=fcd[ b x (ho-x /2)+（b'f-b）h'f(ho-h'f/2)] / γo
641
第 1 页，共 1 页
杭州市萧山区交通规划设计处
-
1
- 6.666667
-
0
- 0.01169
5 受拉钢筋截面积
As mm2 6381
6
7 毛截面积
A mm2 545894
8 换算截面积
Ao mm2 582055

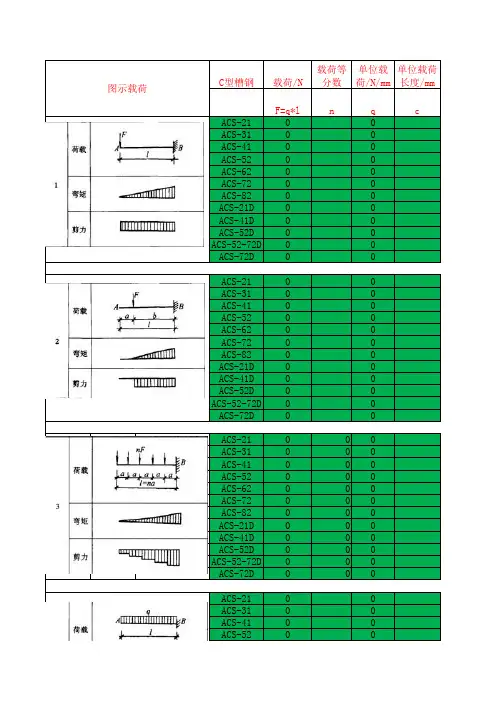
简支梁和悬臂梁的弯矩挠度计算

0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!

第四章简支梁设计计算(1)

第四章简支梁设计计算(1)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第四章简支梁（板）桥设计计算第一节简支梁（板）桥主梁内力计算对于简支梁桥的一片主梁，知道了永久作用和通过荷载横向分布系数求得的可变作用，就可按工程力学的方法计算主梁截面的内力（弯矩M 和剪力Q ），有了截面内力，就可按结构设计原理进行该主梁的设计和验算。

对于跨径在10m 以内的一般小跨径混凝土简支梁（板）桥，通常只需计算跨中截面的最大弯矩和支点截面及跨中截面的剪力，跨中与支点之间各截面的剪力可以近似地按直线规律变化，弯矩可假设按二次抛物线规律变化，以简支梁的一个支点为坐标原点，其弯矩变化规律即为：)(42maxx l x lM M x -=（4-1）式中：x M —主梁距离支点x 处的截面弯矩值；m ax M —主梁跨中最大设计弯矩值；l —主梁的计算跨径。

对于较大跨径的简支梁，一般还应计算跨径四分之一截面处的弯矩和剪力。

如果主梁沿桥轴方向截面有变化，例如梁肋宽度或梁高有变化，则还应计算截面变化处的主梁内力。

一永久作用效应计算钢筋混凝土或预应力混凝土公路桥梁的永久作用，往往占全部设计荷载很大的比重（通常占60～90%），桥梁的跨径愈大，永久作用所占的比重也愈大。

因此，设计人员要准确地计算出作用于桥梁上的永久作用。

如果在设计之初通过一些近似途径（经验曲线、相近的标准设计或已建桥梁的资料等）估算桥梁的永久作用，则应按试算后确定的结构尺寸重新计算桥梁的永久作用。

在计算永久作用效应时，为简化起见，习惯上往往将沿桥跨分点作用的横隔梁重力、沿桥横向不等分布的铺装层重力以及作用于两侧人行道和栏杆等重力均匀分摊给各主梁承受。

因此，对于等截面梁桥的主梁，其永久作用可简单地按均布荷载进行计算。

如果需要精确计算，可根据桥梁施工情况，将人行道、栏杆、灯柱和管道等重力像可变作用计算那样，按荷载横向分布的规律进行分配。

excel计算大全-钢结构计算表格-单跨变截面简支梁

一.1b=100t=10h=230s=6B=#VALUE!mm 2#VALUE!#VALUE!mm#VALUE!mm 3#VALUE!mm 32混凝土等级C208.08板厚h d 100梁跨度6000梁左相邻净距1800梁右相邻净距1800板托顶宽b 0b 1 =600b 2 =6001500mm 150000mm 2#VALUE!mm 2#VALUE!mm混凝土板顶面至组合截面中和轴的距离 x= [b e *h d 2/(2*αE )+A*y]/A 0 =#VALUE!mm混凝土截面惯性矩 I c = b e *h d 3/12=125000000mm 4换算成钢截面的组合截面惯性矩 I 0 = I c /αE + A c *(x-0.5h d )2/αE + I + A(y-x)2 =#VALUE!mm 4#VALUE!mm 4#VALUE!mm 4#VALUE!mm 4#VALUE!mm 43#VALUE!mm 2混凝土板顶面至组合截面中和轴的距离x c = [b e *h d 2/(4*αE )+A*y]/A 0c =#VALUE!mm #VALUE!#VALUE!mm 4#VALUE!mm 4#VALUE!mm 4#VALUE!mm 4二施工阶段的验算1弯矩和剪力钢梁自重：#VALUE!kN/m 板自重： 6.00kN/m 2000mm)板托重：0.90kN/m #VALUE!kN/m自重标准值 g 1：#VALUE!kN/m施工荷载：2.80kN/m钢梁中和轴至钢梁顶面的距离为 y t = [0.5b*t 2 + h*s*(0.5h + t) + B*T*(t+h+0.5T)] / A =钢梁中和轴至钢梁顶面的距离为 y b = h + t + T - y t =钢梁截面惯性矩 I= (b*t 3 + s*h 3 + B*T 3) / 12 + b*t*(yt-0.5t)2 + s*h*(y t -0.5h-t)2 + B*T*(0.5T+h+t-y t )2 =钢梁上翼缘的弹性抵抗矩 W 1 = I / y t =屋面檩条计算截面特征计算钢梁截面特征计算钢梁面积 A ＝b*t + h*s +B*T =混凝土板截面面积A c = b e * h d =换算成钢截面的组合截面面积A 0=A c /αE +A =混凝土板顶面至钢梁截面中和轴的距离 y = h d + h t +y t =对混凝土板顶面的组合截面弹性抵抗矩 w 0c t = αE *I 0 / x=钢梁上翼缘的弹性抵抗矩 W 2 = I / y b =组合截面特征计算钢与混凝土弹性模量比αE =混凝土板计算宽度b e =换算成钢截面的组合截面面积 A 0c = A c / 2αE + A =换算成钢截面的组合截面惯性矩 I 0c = I c /(2*αE ) + A c *(x c -0.5h d )2/(2*αE) + I + A(y-x c )2 =对混凝土板顶面的组合截面弹性抵抗矩 w 0c tc = 2αE *I 0c / x c =对混凝土板底面的组合截面弹性抵抗矩 w 0c bc =2αE *I 0c / (x c - h d ) =对混凝土板底面的组合截面弹性抵抗矩 w 0c b =αE *I 0 / (x - h d ) =对钢梁上翼缘的组合截面弹性抵抗矩 w 0t = I 0 / (d-x) =对钢梁下翼缘的组合截面弹性抵抗矩 w 0b = I 0 / (H-x) =考虑混凝土徐变的组合截面特征计算对钢梁上翼缘的组合截面弹性抵抗矩 w 0tc = I 0c / (d-x c ) =对钢梁下翼缘的组合截面弹性抵抗矩 w 0bc = I 0c / (H-x c ) =(平台梁间距：自重标准值 g 1k ：施工阶段弯矩设计M #VALUE!kN.m 梁跨度：6000mm)施工阶段剪力设计V#VALUE!kN2钢梁抗弯强度设计#VALUE!N/mm 2<215N/mm 2#VALUE!N/mm 2<215N/mm 23钢梁剪应力计算面积矩 S=#VALUE!mm 3#VALUE!N/mm 2<125N/mm 24挠度计算△=5*g*l 4/(384*E*I)=#VALUE!mm < L/400 =15mm三使用阶段的验算1弯矩及剪力找平层重：1.9kN/m 活荷载：15.6kN/m （活荷载：6kn/m 2)78.84kN.m 52.56kN22.1#VALUE!N/mm 2<10N/mm 2#VALUE!N/mm 2<10N/mm 2#VALUE!N/mm 2<215N/mm 2#VALUE!N/mm 2<215N/mm 22.2#VALUE!N/mm 2<10N/mm 2#VALUE!N/mm 2<10N/mm 2#VALUE!N/mm 2<215N/mm 2#VALUE!N/mm 2<215N/mm 22.3(略）2.4(略)3钢梁的剪应力钢梁上翼缘应力 M / r x *W 1 =钢梁下翼缘应力 M / r x *W 2 =钢梁剪应力τ1max = v 1*s 1/I*t w =使用阶段弯矩设计混凝土板底面应力σ0c b =-M/W 0c b =钢梁上翼缘应力σ0t = -M 1/W 1+M 2/W 0t =钢梁下翼缘应力σ0b = -M 1/W 2+M 2/W 0b =考虑混凝土徐变在垂直荷载作用下的正应力使用阶段剪力设计组合梁的抗弯强度在垂直荷载作用下的正应力混凝土板顶面应力σ0c t =-M/W 0c t =钢梁上翼缘应力σ0tc = -M 1/W 1+(M 2g /W 0tc +M 2q /W 0t )=钢梁下翼缘应力σ0bc = -M 1/W 2+(M 2g /W 0bc +M 2q /W 0b )=混凝土板顶面应力:σ0c tc =-(M 2g /W 0c tc +M 2q /W 0c t )=混凝土板底面应力:σ0c bc =-(M 2g /W 0c bc +M 2q /W 0c b )=温度差产生的应力组合梁中由于混凝土收缩引起的内力#VALUE!mm 3#VALUE!mm 3#VALUE!N/mm 2<125N/mm 24组合梁的挠度#VALUE!mm < L/400 =15mm两个受力阶段的荷载对组合梁的钢梁产生的剪应力τ＝V 1S 1/It w +V 2S o /I o T w =△＝5q k l 4/384EI o +5g k l 4/384EI o c =钢梁腹板顶面处对钢梁中和轴的面积矩S 1=钢梁腹板顶面以外的砼及钢梁上翼缘对组合截面中和轴的面积S o =200T=10 mm#VALUE!mm4300板托高度h t150 mm4#VALUE! #VALUE!#VALUE! #VALUE!#VALUE! #VALUE! #VALUE! #VALUE!#VALUE! #VALUE! #VALUE! #VALUE!#VALUE! #VALUE!。

简支梁固有频率计算公式表

简支梁固有频率计算公式表
简支梁的固有频率可以通过以下公式进行计算：
f = (1/2π) sqrt(k/m)。

其中，f代表梁的固有频率，k代表梁的弹性系数，m代表梁的
质量。

在这个公式中，弹性系数k可以通过梁的材料特性和几何形状
来计算，而梁的质量m可以通过梁的密度和几何形状来计算。

另外，对于简支梁来说，其固有频率的计算还需要考虑梁的长
度L和杨氏模量E。

简支梁的固有频率可以通过以下公式进行计算： f = (1/2L) sqrt(E/m)。

在这个公式中，L代表梁的长度，E代表梁的杨氏模量，m代表
梁的质量。

除了上述的公式，还可以通过有限元分析等方法来计算简支梁
的固有频率。

这些方法可以更加精确地考虑梁的几何形状和边界条件等因素，得到更加准确的固有频率值。

总的来说，简支梁的固有频率可以通过多种公式和方法进行计算，需要考虑梁的材料特性、几何形状、边界条件等因素，以得到准确的结果。

简支梁计算(双向板)

梁截面:b=0.24m L= 4.6mh=0.4m h 0=0.375m梁自重： 2.592KN/m梁两侧板：Q （面）= 5.2KN/（m*m）板1：跨度：L1（长）= 4.6mL1（短）= 3.3m板2：跨度：L2（长）= 4.6m L2（短）= 3.3m 27KN/m Q1=29.592KN/m fc=14.3放大系数1a1=1fy=360放大系数12、计算配筋：Q2=8.58KN/m Q （总）=Q1+Q2=38.172KN/m100.9649KN*m0.20920.23737905.18mm*mm=14.0824KN/m Q （总）=Q1+Q2=43.67439KN/m115.5188KN*m0.239360.2781060.09mm*mm=11.3312KN/mQ （总）=Q1+Q2=40.9232KN/m108.2419KN*m0.224280.25741981.576mm*mmξ=1-SQRT(1-2*as)=板传给梁的线荷载为：Q2=(2*L1（长）-0.5*L1（短）)*L1（短）*Q （面）/4/L1（长）+L2（短）*Q （面）/4as=M/（a1*fc*b*h 0*h 0*1000）=M=Q (总）*L*L/8=梁配筋面积As：As=(a1*fc*b*h*ξ*1000000）/fy=(类型三）：当梁一侧板为长垮（板1）；一侧板为短垮（板2）时：Q2=(2*L1（长）-0.5*L1（短）)*L1（短）*Q （面）/4/L1（长）+(2*L2(长)-0.5*L2(短))*L2(短)*Q (面)/4/L2(长)M=Q (总）*L*L/8=梁配筋面积As：as=M/（a1*fc*b*h 0*h 0*1000）=(L1（短）+L2（短）)*Q （面）/4=M=Q (总）*L*L/8=(类型二）：当梁两侧板均为其长垮时：作用在梁上的总荷载：类型（一）：当梁两侧板均为其短垮时：ξ=1-SQRT(1-2*as)=As=(a1*fc*b*h*ξ*1000000）/fy=作用在梁上的总荷载：板传给梁的线荷载为：梁配筋面积As：材料数据：ξ=1-SQRT(1-2*as)=As=(a1*fc*b*h*ξ*1000000）/fy=板传给梁的线荷载为：作用在梁上的总荷载：次梁计算L-1（类型二）1、基本资料：楼板面荷载（包括板自重）：作用在梁上墙体线荷载：as=M/（a1*fc*b*h 0*h 0*1000）=需修改计算结果最终结果KN/（m*m）分类。

excel计算大全-钢结构计算表格-简支钢梁计算

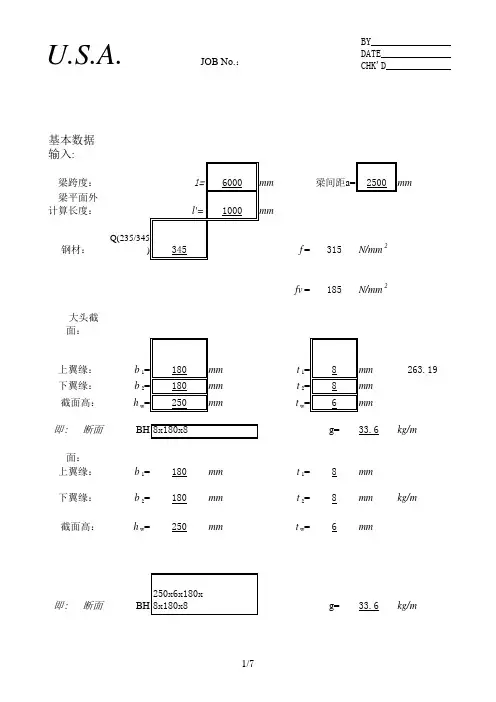
excel计算大全-钢结构计算表格-简支钢梁计算简支钢梁计算基本数据输入:梁跨度： l=9000mm梁间距a=2400mm钢材：Q 345f =315N/mm 2fv =185N/mm 2 上翼缘：b 1=400mm t 1=14mm 下翼缘：b 2=300mm t 2=12mm 腹板：h w =574mm t w =8mm即: 断面BH 600x8x400x14x300x12截面特性计算：钢梁截面：A 0=13792mm 2 重量108.3kg/m 钢梁中和轴的位置：y 0=342mm钢梁对X轴截面惯性矩：I z =8.94E+08mm 4 钢梁上翼缘的弹性抵抗矩：W 1x = 3.46E+06mm 3 钢梁下翼缘的弹性抵抗矩：W 2x = 2.61E+06mm 3钢梁对Y轴截面惯性矩：I y = 1.02E+08mm 4i y =85.9 mm y =104.8上翼缘对Y 轴的惯性矩：I 1=7.47E+07mm 4 下翼缘对Y 轴的惯性矩：I 2= 2.70E+07mm 40.73 截面不对称影响系数：0.380.53 工字形截面简支梁的系数0.76 梁的整体稳定系数：0.74 修正后：0.672.截面验算：（1）弯矩及剪力的计算：=+=211I I I b α=-=)12(8.0b b αη=bβ==hb t l 111ξ=bφ='bφλ钢梁自重： 1.30KN/m恒载： 4.00KN/m2=10.90KN/mg1k活载：q c= 3.0KN/m2p k=18.10KN/m p=23.16KN/m 弯矩：M=234.49KN·m 剪力：V=104.22KN（2）钢梁的强度、稳定和挠度的验算：梁的整体稳定应力：σ=101.01N/mm2钢梁上翼缘应力：σ1=67.70N/mm2钢梁下翼缘应力：σ2=89.68N/mm2钢梁剪应力：τ=22.70N/mm2挠度：w=8.4mmw/l=1/1072。

单跨等截面简支梁钢筋计算表(带公式程序)

KN/m
（2）钢梁的强度、稳定和挠度的验算：
钢梁上翼缘应力：
钢梁下翼缘应力：
钢梁剪应力：
挠度：
σ 1= 263.19 N/mm 2
σ 2=
τ=
w= w / l=
263.19 N/mm 2
45.47 N/mm 2
30.2 mm 1/ 199
2/7
U.S.A.
3.参数统计
1.构件总重：
0.63
0.21 0.18
0.71
14.40 1.00 5/7
U.S.A.
JOB No.：__________
BY________________ DATE______________ CHK'D_____________
6/7
U.S.A.
JOB No.：__________
BY________________ DATE______________ CHK'D_____________
2.截面验算：
（1）弯矩及剪力的验算：
钢梁换算平均自重：
恒载：
0.40 KN/m 4.50 KN/m 2
活载：
g = 1k 11.65 KN/m q c = 2.50 KN/m 2
pk=
弯矩：剪力：
17.90
KN/m
M= V=
p = 22.73
102.30 KN ·m
68.20 KN
JOB No.：__________
BY________________ DATE______________ CHK'D_____________
W 2x = 3.89E+05 mm 3 I y = 7.78E+06 mm 4

简支梁最大挠度计算

按梁的截面查取。自行输入 0 m^4 时，材料类别选项应选择“ 0 m^4 另行输入” 项，使上5行计 0 m^4 算结果为零 0.0000007 m^4 18.9
5 最大挠度 fmax 计算结果单位为米，乘1000后，以毫米单位显示二、单一跨中均布载荷
mm
最大挠度计算公式
A B
简图
a
C
c l
一、单一中置集中载荷
A P C
l/2 l l/2
最大挠度计算公式
B
简图
f max
输入的数据 3500 5000 200 150 单位 Kgf mm GPa GPa 数据
Pl 3 48 EI
单位 N m Pa Pa 按梁的材料查取上结果应为零备注
序号 1 2 3
项目名称符号集中载荷 l 见上图弹性模量 P l E
6
轴惯性矩
I
工字钢
20a 6 轴惯性矩 I 工字钢 10-10 90*90*10 14/9-8 另行输入 7 最大挠度 70
0 cm^4 0 cm^4 0 cm^4 0 cm^4 cm^4
按梁的截面查取。自行输入 0 m^4 时，材料类别选项应选择“ 0 m^4 另行输入” 0 m^4 项，使上5行计算结果为零 0.0000007 m^4 0 m^4 17.5
材料类别 / / 碳钢另行输入
材料规格 / /
用于计算的
34323.8 5.0 2E+11 1.5E&# 工字钢 10-10 90*90*10 14/9-8 另行输入
2370 cm^4 0 cm^4 0 cm^4 0 cm^4 0 cm^4 70 cm^4
0.0000237 m^4 0 m^4

预应力简支梁计算表格

分块面积分块面积分块面积形心到上缘距离分块面积对上缘静矩分块面积自身惯矩di=ys-yi分块面积对截面形心惯矩I=Ii+Ix cm 2cm cm3cm4cm cm4cm4翼板36007.52700067500561136016911427669三角承托15016.667250020847331459331668腹板261087.52283754572938-2414815476054485下三角360153.3551888000-9028917672899767马蹄1080170183********-1061220946312245463∑780049666346846462827440632959052翼板27007.5202505062563.501088772410938349三角承托15016.667250020854.33442842443050腹板261087.52283754572938-16.507104105283347下三角360153.3551888000-82.3024382722446272马蹄1080170183********-99.001058467610620676∑69004899134667771250639232973169463.67cm 71.00cm36.33cm 66.36cm0.57分块面积分块面积分块面积形心到上缘距离分块面积对上缘静矩分块面积自身惯矩di=ys-yi分块面积对截面形心惯矩I=Ii+Ix cm 2cm cm3cm 4cm cm 4cm 4翼板36007.5270006750064.851513962115207121三角承托15016.667250020855.68465080465288腹板207072.51500752281313-0.15472281360下三角360123.3443888000-50.95934545942545马蹄2700155418500520833-82.651844401018964843∑888064246328778553498330337861157翼板27007.5202505062572.161406035914110984三角承托15016.667250020863.00595280595488腹板207072.515007522813137.161062172387530下三角360123.3443888000-43.64685499693499跨中截面小毛截面分块名称大毛截面检验截面效率指标(希望>0.5)上核心距=下核心距=截面效率指标=说明以上初步拟定主梁跨中截面尺寸是合理的小毛截面大毛截面形心到上缘距离ys1=小毛截面形心到上缘距离ys2=变化点截面分块截面几何特性分块名称大毛截面马蹄2700155418500520833-75.341532417415845007∑798063571328609803077152933632508ys1=72.35cm ys2=79.66cm分块面积分块面积分块面积形心到上缘距离分块面积对上缘静矩分块面积自身惯矩di=ys-yi分块面积对截面形心惯矩I=Ii+Ix cm 2cm cm3cm 4cm cm 4cm 4翼板36007.5270006750063.451449317914560679三角承托15016.667250020854.28441994442202腹板891097.586872520214563-26.55628075426495317∑12660898225202822712121592741498198翼板27007.5202505062568.311259730612647931三角承托15016.667250020859.14524608524816腹板891097.586872520214563-21.69419342524407988∑11760891475202653961731533937580736ys1=70.95cm k x =46.20cmys2=75.81cmg=17.25g1=20.18g2=10.96跨中四分点变化点支点α0.500.250.050.00弯距2110.911583.18387.950.00剪力0.00145.58263.05291.16弯距1152.17864.13211.750.00剪力0.0079.46143.58158.92弯距3263.082447.31599.690.00剪力0.00225.04406.62450.08支点Mmax Qmax Mmax Qmax Mmax Qmax Qmax KN.m KN KN.m KN KN.m KN KN 一期恒载2110.910.001583.18145.58387.95263.05291.16二期恒载1152.170.00864.1379.46211.75143.58158.92总恒载=1+23263.080.002447.31225.04599.69406.62450.08汽-201935.88104.331603.57195.59404.70225.05292.50挂-1002350.40162.091913.60266.09490.02276.53277.56恒+汽5198.96104.334050.88420.631004.39631.67742.58恒+挂5613.48162.094360.91491.131089.71683.15727.64分块名称大毛截面二期小毛截面Σ荷载类型恒载内力一期内力组合计算支点截面变化点截面跨中截面四分点截面Sji=1.2*恒+1.4*汽6625.93146.065181.77543.871286.21803.02949.60Sjm=1.2*恒+1.1*挂6501.14178.305041.73562.751258.65792.13845.41汽/6*100%0.37 1.000.400.460.400.360.39提高系数 1.03 1.00 1.03 1.03 1.03 1.00 1.03挂/7*100%0.42 1.000.440.540.450.400.38提高系数 1.00 1.03 1.00 1.02 1.00 1.00 1.00提高后Sji 6824.71146.065337.22560.191324.80803.02978.08提高后Sjm 6501.14183.655041.73574.001258.65792.13845.41钢束其弯高度y1y2L1x3ΦR N1(N2)2112.198.8110099.2571182.35N35112.1938.8110099.2575207.12N4103.325.8877.4210096.59152272.05N512025.8894.1210096.59152762.15N6120.8830.9089.9810095.11181838.41x4(cm)R （cm)sin cos a0(cm)ai(cm)ay(cm)N1(N2)/1182.3599.00N3/5207.1299.00N4/2272.0516.716.70N565.232762.150.023620.999723030.77N682.651838.410.044960.998994243.86N1(N2)71.031182.350.060070.99819911.14N3565.215207.120.108550.99409939.77N4515.342272.050.226820.9739416.775.92N5650.232762.150.235410.9719030107.63y 角度a x5x5*tan(a)a0ai N1(N2)21.007.0032.32 3.979.0026.03N351.0015.0028.637.679.0052.33N4103.3015.0029.307.8516.70112.15N5120.0015.0021.265.7030.00144.30N6RΦ曲线长S 直线长X1直线长L1有效长度预留长度N1(N2)1182.357.00144.451238.97100.002966.85140.00N35207.127.00636.17744.79100.002961.91140.00N42272.0515.00594.82794.66100.002978.96140.00N52762.1515.00723.13659.77100.002965.80140.00N61838.4118.00577.55642.35100.002639.82140.00分块名称分块面积分块面积重心到上缘距离分块面积对上缘静矩全截面重心到上缘距离分块面积自身惯矩di管道面积=46.566n=6n y =毛截面6900.0071.0048991329731694-4.26截面面积和惯矩计算1/4点变化点支点72.17钢束长度计算19.72钢束布置计算各计算截面钢束位置及钢束群位置49.12扣除管道面积-279.40160.72-449050-93.97Σ6667.1744500829731694毛截面7800.0063.67496663329590522.78钢束换算面积230.40160.7237030-94.26Σ8030.4053369332959052毛截面6900.0071.0048991329731694-4.24扣除管道面积-279.40160.28-44781-93.51Σ6667.1744513229731694毛截面7800.0063.67496663329590522.77钢束换算面积230.40160.2836928-93.83Σ8030.4053359132959052毛截面7980.0079.6663571333632508-1.54扣除管道面积-232.83130.88-30474-52.76Σ7747.1760523933632508毛截面8880.0072.35642463378611571.24钢束换算面积192.00130.8825130-57.30Σ9072.0066759337861157毛截面11760.0075.8189147537580736-0.65扣除管道面积-232.83107.83-25106-32.67Σ11527.1786636937580736毛截面12660.0070.95898225414981980.55钢束换算面积192.00107.8320704-36.33Σ12852.0091892941498198b1=180r s =66.75b2=240rs=Ai(cm2)yi(cm)Si(cm3)Ai(cm2)yi(cm)翼板270059159965翼板360059三角承托150507512三角承托15050肋板90494432肋板9049171909下三角3608731171下三角36087马蹄1080103111514马蹄1080104肋板3608329971肋板36084管道-27994-26256管道23094146401翼板270059159965翼板360058三角承托150507512三角承托15049肋板9322624108肋板93225191584-1翼板270059159965翼板360058三角承托150507512三角承托15049肋板9262624098肋板92625191575rs=67rs=Ai(cm2)yi(cm)Si(cm3)Ai(cm2)yi(cm)净轴以上面积对换轴静矩换轴以上面积对换轴静矩静矩变化点支点净截面换算截面翼缘对换轴静矩马蹄部分对换轴静矩截面对重心轴静矩计算净截面翼缘对净轴静矩马蹄部分对净轴静矩净轴以上面积对净轴静矩换轴以上面积对净轴静矩静矩75.1671.501/4点跨中66.7566.46换算截面跨中1/4点66.7666.4578.1273.59净截面换算截面净截面换算截面翼板270059160015翼板360058三角承托150507515三角承托15049肋板90494434肋板9048171963下三角3608731165下三角36088马蹄1080103111494马蹄1080104肋板3608329965肋板36084管道-27994-26128管道23095146496翼板270059160015翼板360058三角承托150507515三角承托15049肋板9322624108肋板93225191637翼板270059160015翼板360058三角承托150507515三角承托15049肋板9262624098肋板92625191628rs=78rs=Ai(cm2)yi(cm)Si(cm3)Ai(cm2)yi(cm)翼板270071190685翼板360066三角承托150619219三角承托15057肋板90615456肋板9056205359下三角3604516275下三角36050马蹄270077207565马蹄270081肋板3604215075肋板36046管道-23353-12284管道23057226632翼板270071190685翼板270066三角承托150619219三角承托15057肋板11363235862肋板108327235765翼板270071190685翼板270066三角承托150619219三角承托15057肋板10553435677肋板102530235580rs=75rs=Ai(cm2)yi(cm)Si(cm3)Ai(cm2)yi(cm)翼板270068182679翼板360064三角承托150588774三角承托15055肋板2705815568肋板27054207021翼板270068182679翼板360064三角承托150588774三角承托15055肋板32493097715肋板324926马蹄部分对换轴静矩净轴以上面积对换轴静矩换轴以上面积对换轴静矩静矩翼缘对换轴静矩支点净轴以上面积对换轴静矩翼缘对换轴静矩马蹄部分对换轴静矩净轴以上面积对换轴静矩换轴以上面积对换轴静矩静矩净轴以上面积对净轴静矩翼缘对净轴静矩马蹄部分对净轴静矩净轴以上面积对净轴静矩换轴以上面积对净轴静矩静矩翼缘对净轴静矩马蹄部分对净轴静矩翼缘对换轴静矩翼缘对净轴静矩净轴以上面积对净轴静矩变化点换轴以上面积对净轴静矩静矩289168翼板270066178443翼板360062三角承托150578538三角承托15053肋板30512886193肋板305125273174跨中四分点变化点支点A j cm 266676667774711527I j cm 427389284274122913300329637337114y js cm 67677875y jx cm 113113102105梁上边缘W js cm 3410350410580422448496776梁下边缘W jx cm 3241840242083323955356130翼缘部分面积S a-j cm 3171909171963205359253200净轴以上面积S j-j cm 3191584191637235765324446换轴以上面积S o-j cm3191575191628235580307763马蹄部分面积S h-j cm 31464011464962266320e j cm98.5193.5152.7632.67A o cm 280308030907212852I o cm 435066653350475203850508941755461y os cm 66.4666.4573.5971.50y ox cm 113.54113.55106.41108.50梁上边缘W os cm3527643527455523250583986梁下边缘W ox cm 3308846308643361850384846翼缘部分面积S a-o cm 3224128220924252332253200净轴以上面积S j-o cm 323064239638217100324446换轴以上面积S o-o cm 3239659239635217836307763马蹄部分面积S h-o cm31948911964842668420e o cm 98.8093.8357.3036.33a ycm14.7419.7249.1272.17θ=Φ-α角度弧度N1(N2)70.127.570.03080.030342.29N3150.267.540.05730.055777.66N4150.267.540.05730.055777.67N513.650.247.460.05270.051471.64N615.420.27 5.810.05700.055477.23N1(N2)70.1214.820.03800.037352.06N3150.2614.790.06450.062587.17N4150.2614.790.06450.062587.18N5150.2614.710.06450.062487.08N6180.3113.060.07280.070297.88跨中换轴以上面积对换轴静矩静矩截面特性汇总1/4点钢束群重心到换轴距离钢束群重心到下缘距离对形心轴静矩名称符号面积对换轴静矩截面管道摩擦损失σs1截面位置钢束x (m)μ*θ+k*x 1-e -(μθ+kx)σk [1-e-(μθ+kx)](Mpa)面积对净轴静矩截面形心至上缘距离截面形心至下缘距离截面抗弯模量单位截面换轴以上面积对净轴静矩静矩截面形心至下缘距离混凝土净截面净面积净惯矩钢束群重心到净轴距离换算截面换算面积换算惯距截面形心至上缘距离截面抗弯模量对形心轴静矩N1(N2)11.560.20 1.720.04000.039354.76N38.770.15 1.690.03080.030342.26N4 1.890.03 1.690.00800.007911.06N5 1.380.02 1.610.00620.00628.63N1(N2)000.320.00030.00030.45N3000.290.00030.00030.40N4000.290.00030.00030.41N5000.210.00020.00020.30钢束N1(N2)N3N4N5N6l(mm)31068.4931019.1431189.5831057.9927798.16σs2(Mpa)73.3973.5073.1073.4182.02σy0σy0*Δay cos αN y0A j =6667I j =27412291N21279.3210746.30110746.3010746.30103.751114928.70N11246.8310473.40110473.4021219.70103.751086615.52N51195.5410042.560.99972110810039.7631259.4681.98823059.59N31153.959693.1419693.1440952.60103.751005663.14N41131.349503.2619503.2650455.8796.05912788.38Aj=6667Ij=27389284.01N21269.5510664.22110664.2210664.22103.761106519.33N11237.2910393.20110393.2021057.42103.761078398.71N51179.699909.3619909.3630966.7882.76820098.48N31144.369612.6619612.6640579.44103.76997409.44N41131.269502.6019502.6050082.0496.05912724.49Aj=7747Ij=33003295.98N21266.8610641.590.99819400710622.3710622.3790.86965148.32N11244.4110453.080.99819400710434.2021056.5790.86948051.50N51299.6410916.960.97189685810610.1631666.73-5.63-59735.21N31230.3810335.190.9940914110274.1241940.8583.37856553.64N41268.7510657.470.97393711710379.7152320.5626.08270702.82A=8030.4Io=35047519.92N611235.7510380.280.99898900210369.7869.69722721.48N2914.407680.9317680.93104.55803069.23N1914.937685.3917685.39104.55803534.73N5888.337461.960.9997211087459.8882.78617553.08N3882.687414.5217414.52104.55775214.85N4881.477404.3817404.3896.54714783.45N6890.037476.230.9989890027468.6769.69520528.85Σ45113.774234684.19A=8030.4Io=35066652.86成桥后张拉N61/4点跨中变化点1/4点支点锚具变形，钢束回缩引起的损失σs2（Mpa)截面σs4计算表钢束号锚固时预加纵向轴力N y0ΣNy0(0.1KN)e yi M y0=Ny0*eyi变化点N611235.7510380.27515110380.2751571.54742614.5091N2929.797810.24333317810.243333104.54816490.0799N1891.347487.28532117487.285321104.54782727.7499N5892.207494.47881917494.47881983.54626095.7096N3896.707532.25247817532.252478104.54787428.6581N4892.307495.27927917495.27927996.87726074.6536N6890.987484.22985217484.22985271.54535428.7432Σ45303.769084274245.594σs5=0.045*139562.775截面Ny(Mpa)My(Mpa)Mg(Mpa)My-Mg I (m 4) A (m 2)e (m)Ny/A 跨中5008.204915.152110.912804.240.273892840.670.997.511/4点5045.594943.061583.18253359.870.2741229050.670.947.57变化点5232.062980.72387.94562592.780.330032960.770.53 6.75βα(τ)=0.312u=818.74h=λ*2*Ah/u=28.58查表Φf2= 1.61Φf =2*1.61= 3.22Φ(∞,т)=Φ(t,т)= 2.77ε=0.23*10^3配筋率跨中1/4点变化点A (cm 2)8030.408030.409072.00Ay (cm2)50.4050.4050.40μ0.010.010.01跨中1/4点变化点r 24366.744364.364244.39e A98.8093.8357.30e A 29761.628804.463282.83ρ3.24 3.02 1.771+10*μ*ρ 1.20 1.19 1.10Φ(∞,т) 2.773 2.773 2.773ε=0.000230.000230.00023σh17.6019.0310.90n*σh*Φ(∞,т)271.86293.98168.36Ey*ε42.5542.5542.55n*σh*Φ(∞,314.41336.53210.91261.34282.94192.00σs6 (Mpa)分母分子混凝土收缩须变损失σs6σh的计算跨中σs1σs2σs4N11395.0052.0673.3932.261237.29N21395.0052.0673.390.001269.55N31395.0087.1773.5089.961144.36N41395.0087.1873.10112.971121.75N51395.0087.0873.4154.831179.69N61395.0097.8882.021215.10N11395.0054.7673.3922.441244.41N21395.0054.7673.390.001266.86N31395.0042.2673.5048.861230.38N41395.0011.0673.1042.091268.75N51395.008.6373.4113.321299.64截面M (KN.m)N (KN)σs5+σs6N y N y1M'M y1变化点2980.7252320.560.005232.060.002980.72（一）混凝土法向应力的验算梁截面下缘最大压应力бha ≤0.75R ab’＝0.75×0.9×35＝23.625MPa 梁截面上缘最大拉应力бhl ≤0.75R lb’＝0.70×0.9×3.0＝1.89MPa 截面应力部位M g1 （kN·m）N y0(kN)M y0(kN·m)A j （m 2）I 1（m 4)e 1s e 1x (m)上缘0.67下缘 1.13上缘0.67下缘 1.13上缘0.78下缘1.02采用两定点吊装。

简支梁侧立柱大小计算公式表

简支梁侧立柱大小计算公式表
简支梁侧立柱的大小计算需要考虑多个因素，包括梁的跨度、荷载大小、立柱的材料和规格等。

以下是一些常用的计算公式表：
1. 立柱截面面积计算公式
立柱截面面积=荷载/(材料的允许应力×安全系数)
其中，荷载指的是梁上的荷载，材料的允许应力是指材料能承受的最大应力值，安全系数是为了保证结构的安全而设置的系数。

2. 立柱截面尺寸计算公式
立柱截面尺寸=根号[(4×截面面积)/(π×立柱高度)]
其中，截面面积指的是立柱的横截面积，立柱高度是指立柱从地面到梁底的高度。

该公式可以帮助计算出立柱的直径或者边长。

3. 立柱弯矩计算公式
立柱弯矩=荷载×立柱高度/4
弯矩是指立柱受到的力矩大小，可以通过该公式计算出。

总之，在进行简支梁侧立柱大小计算时，需要综合考虑多个因素，如荷载大小、立柱材料、立柱高度等，同时需要根据具体情况选择合适的计算公式。

T梁、简支梁等的配筋计算

梁宽度梁高度
b= h= h0=
250 600
mm mm mm 540 mm 3.75 kN/m 14.3 N/㎜2 1.43 N/㎜2 a1= b1= ξ
b=
as= 60 梁自重混凝土选用
a's= 35
mm
C 30 fc = ft= 1 0.8 0.550
钢筋选用 fy=f'y=
2
其中，1; HPB235级钢 2; HRB335级钢 3; HRB400级钢
3
为充分发挥受压钢筋A's的作用，取As2=A's=
942.48 mm2
AS1 =
a1 fcb
fy
2 (h0 - h0 -
2M )= a1 fcb
-376.55 ㎜2
纵向受拉钢筋总截面面积 As＝As1＋As2= 受拉钢筋取钢筋直径实配钢筋面积AS= 2α 's＝
565.93 实取
2
㎜2
20
￠＝
8
纵向受拉钢筋总截面面积 As＝As1＋As2= 2399.42 ㎜2 受拉钢筋取钢筋直径
20
￠＝
2
实取
9 2
mm ≤
根
实配钢筋面积AS= 2827.43 mm 受压钢筋取钢筋直径 12 ￠＝实取实配钢筋面积AS= 2α 's＝ 226.19 mm 70.00 mm
2
OK!
根
OK!
x
验算受压区高度x＝fyAs1/(α1fcb)=
AS =
a1 fcb 2M (h0 - h02 )= fy a1 fcb
￠＝
取钢筋直径
18
1017.88 mm2
4
实配钢筋面积AS= Asmin=

简支T梁(30m)横向分布系数计算

Ixx= J=
0.418 0.0147
m**4 m**4
二、抗弯刚度修正由于结构是多跨连续梁（本文假定是3x30简支转连续T梁），所以应该考虑抗弯刚度修正系数.，简支梁不考虑抗弯修正系数
1、抗弯刚度换算系数K的计算：
0 K=δ /δ
中跨：边跨=30 ：30= 1 : 1 由《梁桥下册》P204页刚度修正系数表：
人行道
分隔带
车行道
中央分隔带
车行道
分隔带
人行道
0.5
0
左车道数 = 2, 右车道数 = 0, 不计车道折减
汽车等级: 汽车 -20级挂车等级: 无挂车荷载人群集度: 0.000 KPa ----------------------------------------------------影响线数值:
l1边跨l1中跨l2边跨l1中跨l2边跨l1中跨l2081497178911392139214291818143218611136614171404187614041891213431442138218311381191914130614481344203413411974151291511328207913242161276152913142125130920221812521567128922091282207921231161267228612622105内插得项目边跨中跨k14291818则在计算边跨横向力分布系数边跨的中梁和边梁的抗弯惯矩需要乘以1429中梁修正抗弯惯距0604边梁修正抗弯惯距0597而在计算中跨横向力分布系数中跨的中梁和边梁的抗弯惯矩需要乘以1818中梁修正抗弯惯距0769边梁修正抗弯惯距0760三左板惯矩右板惯矩计算中跨
主梁跨径: 30.000 m

局部荷载转化为均布荷载计算表(简支梁原表)

1.70 3.40 5.10
2.30 4.60
6.80
6.90
8.00 9.00 10.00
8.50 9.20
2800 6.90
2800 0.00
2800 0.00
2800 0.00
2800 0.00
2800 0.00 6.90
3200 4.60
3200 0.00
3200 0.00
3200 0.00
3200 0.00
3200 0.00 4.60
3600 2.30
3600 0.00
3600 0.00
3600 0.00
一、截面信息板长l(mm)
4000
二、一个集中力P
P(KN)
10
距左端距离a(mm)
左端支座反力RA=Pb/l(KN)
4.25
距左端距离 x (mm)
0
400
弯距Mx(KN·m)
0.00
1.70
二、一个集中力P
P(KN)
0
距左端距离a(mm)
左端支座反力RA=Pb/l(KN)
0
距左端距离 x (mm)
0
400
弯距Mx(KN·m)
0.00
0.00
二、一个集中力P
P(KN)
0
距左端距离a(mm)
左端支座反力RA=Pb/l(KN)
0
距左端距离 x (mm)
0
400
弯距Mx(KN·m)
0.00
0.00
三q 、(均K一N部/段m中)均点部距荷左0载端q距离a(距m左m)端d(m最m近)1距70离0
左端支座反力RA=qcb/l(KN)
左端支座反力RA=qcb/l(KN)

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4/7
U.S.A.
钢梁上翼缘的弹性抵抗矩：
钢梁下翼缘的弹性抵抗矩：
钢梁对Y 轴截面惯性矩：
上翼缘对 Y轴的惯性矩：
下翼缘对 Y轴的惯性矩：
平面外稳定系数计算：
截面不对称影响系数：
工字形截面简支梁的系数
JOB No.：__________
BY________________ DATE______________ CHK'D_____________
钢梁截面钢：梁中和轴的位置：
钢梁对X 轴截面惯性矩：
钢梁上翼缘的弹性抵抗矩：
钢梁下翼缘的弹性抵抗矩：
钢梁对Y 轴截面惯性矩：
上翼缘对 Y轴下的翼惯缘性对 Y轴的惯性
截面特性计算：
钢梁截面钢：梁中和轴的位置：
钢梁对X 轴截面惯性矩：
A 0 = 7884 mm 2 重量 61.9 y 0 = 425 mm
t 1= 8 mm t 2= 8 mm t w= 6 mm
t 1= 8 mm t 2= 8 mm t w= 6 mm
kg/m
1/7
U.S.A.
JOB No.：__________
即 : 断面
350x6x180x BH 8x180x8
BY________________ DATE______________ CHK'D_____________
U.S.A.
JOB No.：__________
BY________________ DATE______________ CHK'D_____________
基本数据输入:
梁跨度：梁平面外计算长度：
l= 18000 mm l'= 3500 mm
梁间距a= 6000 mm
钢材： (235/345) 235
BY________________ DATE______________ CHK'D_____________
1.22 0.81
6/7
U.S.A.
JOB No.：__________
BY________________ DATE______________ CHK'D_____________
kg/m 7/7
2.截面验算：
（1）弯矩及剪力的验算：
钢梁换算平均自重：
恒载：
活载：
0.65 KN/m
0.25 KN/m 2
g = 1k 2.15 KN/m q c = 0.35 KN/m 2
pk=
弯矩：剪力：
4.25
KN/m
p = 5.52
M = 223.49 KN ·m
V = 49.66 KN
KN/m
f = 215 N/mm 2
大头截面：
fv = 125 N/mm 2
上翼缘：下翼缘：截面高：
即 : 断面小头截面：
上翼缘：
下翼缘：
截面高：
b 1= 180 mm b 2= 180 mm h w= 850 mm
850x6x180x BH 8x180x8
b 1= 180 mm b 2= 180 mm h w= 350 mm
W 1x = 5.88E+05 mm 3
W 2x = 5.88E+05 mm 3 I y = 7.78E+06 mm 4
iy=
46.5 mm
y=
75.3
I 1 = 6.67E+06 mm 4
I 2 = 3.89E+06 mm 4
0.63 0.21 0.18
0.71 5/7
U.S.A.
JOB No.：__________
I z = 8.01E+08 mm 4
W 1x = 1.88E+06 mm 3 W 2x = 1.88E+06 mm 3
I y = 7.79E+06 mm 4
iy=
36.6 mm
y=
95.7
I 1 = 6.67E+06 mm 4
I 2 = 3.89E+06 mm 4
A 0 = 4884 mm 2 重量 38.3 y 0 = 175 mm I z = 1.03E+08 mm 4
（2）钢梁的强度、稳定和挠度的验算：钢梁上翼缘应力：
钢梁下翼缘应力：
σ 1= 145.75 N/mm 2 σ 2= 118.65 N/mm 2 2/7
U.S.A.
钢梁剪应力挠：度：
3.参数统计
1.构件总重：
2.构件实际重量：
JOB No.：__________
BY________________ DATE______________ CHK'D_____________
τ= w= w / l=
23.65 N/mm 2 62.4 mm
1/ 288
扩大系
ቤተ መጻሕፍቲ ባይዱ
902.1 Kg
数：
1.2
1082.5 Kg
3/7
U.S.A.
JOB No.：__________
BY________________ DATE______________ CHK'D_____________
截面特性计算：