2019最新第八章商业银行数学

1、1694年在政府的助下，英国建立了历史上第一家资本主义股份制的商业银行------英格兰银行。

2、清政府于1897年在沪成立中国通商银行，标志着中国现代银行的产生。

3、内部经营风险是由企业经营状况、管理水平等多种因素引起的，主要包括个人风险、财产风险、经营风险和责任风险。

4、《新巴塞尔资本协议》的最低资本要求包括：1、核心资本（一级资本）与风险加权资产的比率不得低于4%。

2、总资本（一级资本与二级资本之和）与风险加权资产的比率不得低于8%，二级资本最高不得超过一级资本的100%。

5、《新巴塞尔资本协议》的主要精神《新巴塞尔资本协议》的主要精神是银行风险监管的三大支柱。

第一支柱是最低资本要求。

第二支柱是监管当局的监督检查。

第三支柱是市场纪律。

6、商业银行的作用：信用中介、支付中介、信用创造、金融服务。

7、商业银行的外部组织形式：商业银行的外部组织形式是指商业银行在社会经济生活中的存在形式。

主要有三种类型：1、单一银行制。

2、分行制。

3、银行控股公司制。

8、现金资产的构成1、库存现金。

2、托收中的现金。

3、在中央银行的存款。

4、存放同业存款。

9、现金资产管理的原则：1适度存量控制原则。

2适时流量调节原则。

3安全性原则。

10、流动性需求管理的原则：1、进取型原则。

2、保守型原则。

3、成本最低原则。

11、贷款分类：1、正常类。

2、关注类。

3、次级类。

4、可疑类。

5、损失类。

12、企业贷款的种类：1、短期贷款。

2、定期贷款。

3、小企业贷款。

4、农业贷款。

13、“5C”判断法：品质（character），能力(capacity)，资本(capital)，担保品(collateral)，环境(conditions)14、商业银行证券投资的功能:1获取利益。

2管理风险。

3增强流动性。

4管理风险资本。

15、中间业务的特点。

1、表外性。

2，多样性。

3，风险差异性。

16，票据从种类上来讲与支票，汇票和本票三种。

17，商业银行的海外业务机构形式：有代表处，代理处，海外分支行（境外联行），附属银行子银行），代理银行，联营银行，银团银行等七种形式。

高考专题突破四高考中的立体几何问题【考点自测】1．在正三棱柱ABC－A1B1C1中，D为BC的中点，E为A1C1的中点，则DE与平面A1B1BA的位置关系为________．答案平行解析如图取B1C1的中点为F，连结EF，DF，则EF∥A1B1，DF∥B1B，且EF∩DF＝F，A1B1∩B1B＝B1，∴平面EFD∥平面A1B1BA，∴DE∥平面A1B1BA.2．设x,y，z是空间中不同的直线或平面，对下列四种情形：①x,y，z均为直线；②x，y是直线，z是平面；③z是直线，x，y是平面;④x，y，z均为平面．其中使“x⊥z且y⊥z⇒x∥y”为真命题的是________．(填序号)答案②③解析由正方体模型可知①④为假命题;由线面垂直的性质定理可知②③为真命题．3．一个六棱锥的体积为2错误!，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为________．答案12解析设六棱锥的高为h，则V＝错误!Sh，所以错误!×错误!×4×6h＝2错误!,解得h＝1.设六棱锥的斜高为h′，则h2＋（3）2＝h′2,故h′＝2.所以该六棱锥的侧面积为错误!×2×2×6＝12.4．设α，β,γ是三个平面，a，b是两条不同的直线,有下列三个条件：①a∥γ，b⊂β;②a∥γ，b∥β；③b∥β，a⊂γ.如果命题“α∩β＝a，b ⊂γ，且________，则a∥b”为真命题，则可以在横线处填入的条件是________．（把所有正确的序号填上)答案①或③解析由线面平行的性质定理可知，①正确；当b∥β，a⊂γ时，a 和b在同一平面内，且没有公共点，所以平行，③正确．故应填入的条件为①或③.5．如图，以等腰直角三角形ABC的斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：①BD⊥AC；②△BAC是等边三角形；③三棱锥D－ABC是正三棱锥;④平面ADC⊥平面ABC.其中正确的是________．(填序号）答案①②③解析由题意知，BD⊥平面ADC，故BD⊥AC，①正确;AD为等腰直角三角形斜边BC上的高,平面ABD⊥平面ACD，所以AB＝AC ＝BC，△BAC是等边三角形,②正确;易知DA＝DB＝DC，又由②知③正确；由①知④错。

§8.6空间向量及其运算最新考纲考情考向分析1。

了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的正交分解及其坐标表示．2.掌握空间向量的线性运算及其坐标表示．3.掌握空间向量的数量积及其坐标表示，能运用向量的数量积判断向量的共线和垂直.本节是空间向量的基础内容，涉及空间直角坐标系、空间向量的有关概念、定理、公式及四种运算等内容．一般不单独命题，常以简单几何体为载体；以解答题的形式出现,考查平行、垂直关系的判断和证明及空间角的计算，解题要求有较强的运算能力.1．空间向量的有关概念名称概念表示零向量模为0的向量0单位长度(模）为1的向量2.空间向量中的有关定理（1)共线向量定理空间两个向量a与b(b≠0)共线的充要条件是存在实数λ，使得a＝λb。

(2）共面向量定理共面向量定理的向量表达式：p＝x a＋y b，其中x，y∈R，a，b为不共线向量．(3)空间向量基本定理如果三个向量a，b，c不共面，那么对空间任一向量p，存在有序实数组｛x，y，z｝，使得p＝x a＋y b＋z c,｛a，b,c}叫作空间的一个基底．3．空间向量的数量积及运算律(1）数量积及相关概念①两向量的夹角已知两个非零向量a,b，在空间任取一点O，作错误!＝a，错误!＝b，则∠AOB叫作向量a,b的夹角,记作〈a，b>，其范围是0≤〈a，b>≤π,若〈a，b〉＝错误!，则称a与b互相垂直，记作a⊥b。

②两向量的数量积已知空间两个非零向量a，b，则｜a｜｜b|cos<a，b〉叫作向量a,b 的数量积，记作a·b，即a·b＝｜a｜|b|cos〈a，b〉．(2）空间向量数量积的运算律①（λa)·b＝λ（a·b）；②交换律:a·b＝b·a；③分配律：a·(b＋c）＝a·b＋a·c。

4．空间向量的坐标表示及其应用设a＝（a1,a2,a3)，b＝(b1,b2，b3）。

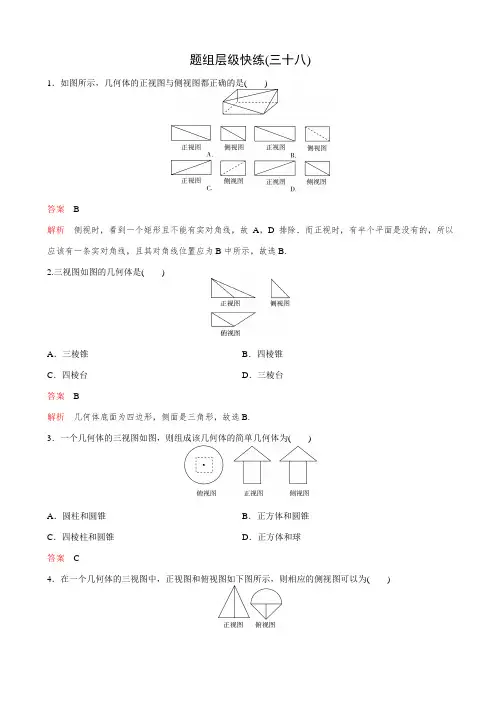
题组层级快练(三十八)1．如图所示，几何体的正视图与侧视图都正确的是()答案 B解析侧视时，看到一个矩形且不能有实对角线，故A，D排除．而正视时，有半个平面是没有的，所以应该有一条实对角线，且其对角线位置应为B中所示，故选B.2.三视图如图的几何体是()A．三棱锥B．四棱锥C．四棱台D．三棱台答案 B解析几何体底面为四边形，侧面是三角形，故选B.3．一个几何体的三视图如图，则组成该几何体的简单几何体为()A．圆柱和圆锥B．正方体和圆锥C．四棱柱和圆锥D．正方体和球答案 C4．在一个几何体的三视图中，正视图和俯视图如下图所示，则相应的侧视图可以为()答案 D解析 根据分析，只能是选项D 中的视图．故选D.5．若已知△ABC 的平面直观图△A ′B ′C ′是边长为a 的正三角形，则原△ABC 的面积为( )A.32a 2B.34a 2C.62a 2 D.6a 2 答案 C解析 如图所示是△ABC 的平面直观图△A ′B ′C ′.作C ′D ′∥y ′轴交x ′轴于D ′，则C ′D ′对应△ABC 的高CD ，∴CD ＝2C ′D ′＝2·2·C ′O ′＝22·32a ＝6a.而AB ＝A ′B ′＝a ，∴S △ABC ＝12·a ·6a ＝62a 2.6．(2015·安徽)一个四面体的三视图如图所示，则该四面体的表面积是( )A ．1＋ 3B ．2＋ 3C ．1＋2 2D ．2 2答案 B解析 在长、宽、高分别为2、1、1的长方体中，该四面体是如图所示的三棱锥P －ABC ，表面积为12×1×2×2＋34×(2)2×2＝2＋ 3.7．某几何体的正视图与侧视图如图所示，若该几何体的体积为13，则该几何体的俯视图可以是( )答案 D解析 通过分析正视图和侧视图，结合该几何体的体积为13，可知该几何体的底面积应为1，因此符合底面积为1的选项仅有D 选项，故该几何体为一个四棱锥，其俯视图为D.8. (2016·兰州诊断考试)某几何体的三视图如图所示，且该几何体的体积是3，则正视图中x 的值是( )A ．2 ` B.92 C.32 D ．3答案 D解析 由三视图知，该几何体是四棱锥，底面是一个直角梯形，底面积S ＝12×(1＋2)×2＝3，高h ＝x ，所以其体积V ＝13Sh ＝13×3x ＝3，解得x ＝3，故选D.9．(2016·南京质检)某四面体的三视图如图所示，该四面体四个面的面积中最大的是( )A ．8B ．6 2C ．10D ．8 2答案 C解析 由三视图可知，该几何体的四个面都是直角三角形，面积分别为6，62，8，10，所以面积最大的是10，故选择C.10．某几何体的三视图如图所示，则该几何体中，最大侧面的面积为( )A.12B.22 C.52 D.62 答案 C解析 由三视图知，该几何体的直观图如图所示．平面AED ⊥平面BCDE ，四棱锥A －BCDE 的高为1.四边形BCDE 是边长为1的正方形，则S △AED ＝12×1×1＝12，S △ABC ＝S △ABE ＝12×1×2＝22，S △ACD ＝12×1×5＝52，故选C.11．(2016·人大附中模拟)已知矩形ABCD 的顶点都在半径为R 的球O 的球面上，AB ＝6，BC ＝23，棱锥O －ABCD 的体积为83，则球O 的表面积为( ) A ．8π B ．16π C ．32π D ．64π答案 D解析 由题意可知矩形ABCD 所在截面圆的半径r ＝62＋（23）22＝23，S 矩形ABCD ＝12 3.设球心O 到平面ABCD 的距离为h ，则13×123×h ＝83，解得h ＝2，∴R ＝r 2＋h 2＝4，∴S 球O ＝4πR 2＝64π.12．已知三棱锥的正视图与俯视图如图所示，俯视图是边长为2的正三角形，那么该三棱锥的侧视图可能为( )答案 B解析 这个空间几何体的直观图如图所示，由题知，这个空间几何体的侧视图的底面一边长是3，故其侧视图只可能是选项B 中的图形．13．(2016·江西九江模拟)如图，网格纸上小正方形边长为1，粗线是一个棱锥的三视图，则此棱锥的表面积为( )A ．6＋42＋2 3B ．8＋4 2C ．6＋6 2D ．6＋22＋4 3答案 A解析 直观图是四棱锥P －ABCD ，如图所示，S △PAB ＝S △PAD ＝S △PDC ＝12×2×2＝2，S △PBC ＝12×22×22×sin60°＝23，S 四边形ABCD ＝22×2＝42，故选A.14．(2016·沧州七校联考)如图所示，某几何体的正视图(主视图)是平行四边形，侧视图(左视图)和俯视图都是矩形，则该几何体的体积为( )A．6 3 B．9 3C．12 3 D．18 3答案 B解析由几何体的三视图知直观图如图所示．原几何体是底面ABCD为矩形的四棱柱，且AB＝3，侧面A1ABB1⊥底面ABCD，A1A＝2.过A1作A1G⊥AB于G，由三视图知AG＝1，A1D1＝3，A1G＝A1A2－AG2＝ 3.底面ABCD的面积S＝3×3＝9，V ABCD－A1B1C1D1＝S·h＝9×3＝9 3.15. (2016·北京西城区期末)已知一个正三棱柱的所有棱长均相等，其侧(左)视图如图所示，那么此三棱柱正(主)视图的面积为________．答案2 3解析由正三棱柱三视图还原直观图可得正(主)视图是一个矩形，其中一边的长是侧(左)视图中三角形的高，另一边是棱长．因为侧(左)视图中三角形的边长为2，所以高为3，所以正视图的面积为2 3.16．(2016·名师改编)已知某组合体的正视图与侧视图相同，如图所示，其中AB＝AC，四边形BCDE为矩形，则该组合体的俯视图可以是________．(把你认为正确的图的序号都填上)答案 ①②③④17．已知正三棱锥V －ABC 的正视图、侧视图和俯视图如图所示．(1)画出该三棱锥的直观图； (2)求出左视图的面积． 答案 (1)略 (2)6解析 (1)如右图所示．(2)根据三视图间的关系可得BC ＝23， ∴左视图中VA ＝42－（23×32×23）2＝2 3.∴S △VBC ＝12×23×23＝6.1．(2014·福建理)某空间几何体的正视图是三角形，则该几何体不可能是( ) A ．圆柱 B ．圆锥 C ．四面体 D ．三棱柱答案 A解析 因为圆锥、四面体、三棱柱的正视图均可以是三角形，而圆柱无论从哪个方面看均不可能是三角形，所以选A.2．(2013·辽宁)已知直三棱柱ABC －A 1B 1C 1的6个顶点都在球O 的球面上．若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径为( ) A.3172B ．210 C.132 D ．310答案 C解析 由题设可知该三棱柱可以看作长方体的一部分，且该长方体同一顶点的三条棱长分别为3，4，12，三棱柱的外接球，即为长方体的外接球，故(2R)2＝32＋42＋122，R ＝132，选C.3.(2016·湖南怀化一中模拟)沿一个正方体三个面的对角线截得的几何体如图所示，则该几何体的左(侧)视图为()答案 B解析由三视图定义可知选B.4．(2014·新课标全国Ⅰ理)如图所示，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为()A．6 2 B．6C．4 2 D．4答案 B解析将三视图还原为几何体再计算，几何体为三棱锥．如图，侧面SBC⊥底面ABC.点S在底面ABC的射影点O是BC的中点，△ABC为直角三角形．∵AB＝4，BO＝2，∴AO＝20，SO⊥底面ABC.∴SO⊥AO，SO＝4.∴最长的棱AS＝20＋16＝6.5.(2016·东北四校模拟)如图所示，三棱锥的底面是直角三角形，直角边长分别为3和4，过直角顶点的侧棱长为4，且垂直于底面，该三棱锥的正视图是()答案 B解析 三棱锥的正视图应为高为4，底边长为3的直角三角形．6. (2016·衡水调研卷)如图所示，在三棱柱ABC —A 1B 1C 1中，AA 1⊥平面ABC ，A 1A ＝AB ＝2，BC ＝1，AC ＝5，若规定主(正)视方向垂直平面ACC 1A 1，则此三棱柱的侧(左)视图的面积为( )A.455B ．2 5C ．4D ．2答案 A解析 过B 作BD ⊥AC 于D ，过点B 1作B 1D 1⊥A 1C 1于D 1连接DD 1，则三棱锥的侧视图就是矩形BDD 1B 1，且BD ＝25，BB 1＝2.所以，其面积为S ＝25×2＝45 5.7.如图所示，在正方体ABCD －A ′B ′C ′D ′中，M ，E 是AB 的三等分点，G ，N 是CD 的三等分点，F ，H 分别是BC ，MN 的中点，则四棱锥A ′－EFGH 的侧视图为( )答案 C解析 注意分清三等分点可以看出，侧视图中A ′E ，A ′G 重合，A ′H 成为A ′M ，A ′F ，A ′B 重合，侧视图为向左倾斜的三角形，故选C.8.如图所示，正方形O ′A ′B ′C ′的边长为1 cm ，它是水平放置的一个平面图形的直观图，则原图形的周长是________ cm.答案 8解析 根据直观图的画法可知，在原几何图形中，OABC 为平行四边形，且有OB ⊥OA ，OB ＝22，OA ＝1，所以AB ＝3.从而原图的周长为8 cm.9．如图所示，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为________．答案 2 3解析 将几何体的三视图还原为直观图：四棱锥P －ABCD ，如图将直观图补成一个正方体，显然最长的一条棱的长PB ，即为正方体的对角线长，易知正方体的棱长为2，所以对角线长为2 3.10．已知球O 是棱长为1的正方体ABCD －A 1B 1C 1D 1的内切球，则以球心O 为顶点，以球O 被平面ACD 1所截得的圆为底面的圆锥的体积为________．答案 3π108解析 连接B 1D ，则B 1D 过点O ，设B 1D 交平面ACD 1于点M ，如图，易知B 1D233，则OM ＝⊥平面ACD 1，∴B 1M ⊥平面ACD 1，∵B 1D ＝3，∴B 1M ＝23B 1D ＝圆，设内切圆233－32＝36，而球O 被平面ACD 1所截得的圆是△ACD 1的内切半径为r ，则S △ACD 1＝12×2×2sin60°＝12×(2＋2＋2)×r ，即r ＝66，∴所求圆锥的体积V ＝13[π×(66)2]×36＝3π108. 11．一个空间几何体的三视图如图所示，其主(正)视图是正三角形，边长为1，左(侧)视图是直角三角形，两直角边分别为32和12，俯视图是等腰直角三角形，斜边为1，则此几何体的体积为________．答案324解析 根据三视图可知此空间几何体为三棱锥，其底面面积为S ＝12×1×12＝14，三棱锥的高为h ＝32，所以几何体的体积为V ＝13Sh ＝13×14×32＝324.。