控制工程基础---第四章传递函数
- 格式:doc
- 大小:178.24 KB
- 文档页数:9

自动控制原理传递函数知识点总结自动控制原理是研究自动控制系统中信号传递、处理、转换等基本理论和方法的学科。
传递函数是描述线性时不变系统的数学模型,它对于分析和设计控制系统起着重要的作用。
下面将对自动控制原理中关于传递函数的知识点进行总结。
一、传递函数的定义传递函数是用来描述线性时不变系统输入-输出关系的数学函数。
对于连续时间系统,传递函数可以表示为:G(s) = Y(s) / X(s)其中,G(s)为传递函数,Y(s)为系统的输出信号,X(s)为系统的输入信号,s为复变量。
对于离散时间系统,传递函数可以表示为:G(z) = Y(z) / X(z)其中,G(z)为传递函数,Y(z)为系统的输出信号,X(z)为系统的输入信号,z为复变量。
二、传递函数的性质1. 时域特性:传递函数可以通过拉氏变换将时域的微分、积分方程转换为频域的代数方程,从而简化系统的分析和设计。
2. 稳定性:传递函数的稳定性与其极点位置有关。
当所有极点均位于左半平面时,传递函数是稳定的;当存在极点位于右半平面时,传递函数是不稳定的。
3. 零点和极点:传递函数的零点是使得传递函数为零的点,极点是使得传递函数无穷大的点。
零点和极点的位置对系统的动态性能和稳定性有重要影响。
4. 频率响应:传递函数的频率响应是指系统对不同频率输入信号的响应特性。
频率响应可以通过传递函数的频域分析获得,包括幅频特性和相频特性。
三、传递函数的常见形式1. 一阶系统传递函数:一阶系统的传递函数形式为:G(s) = K / (s + a)其中,K为传递函数的增益,a为系统的时间常数。
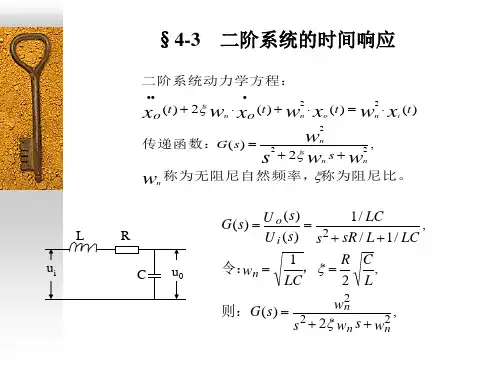
2. 二阶系统传递函数:二阶系统的传递函数形式为:G(s) = K / (s^2 + 2ζω_ns + ω_n^2)其中,K为传递函数的增益,ζ为阻尼比,ω_n为自然频率。
3. 传递函数的因果性:因果系统的传递函数在复平面上的极点全部位于左半平面,即Re(s) < 0。
非因果系统的传递函数在复平面上的极点存在于右半平面,即Re(s) > 0。


第四章 传递函数第一节 传递函数的概念与性质一、传递函数的概念对于单输入、单输出的线性定常系统,传递函数定义为“当输入量和输出量的一切初始值均为零时,输出量的拉氏变换和输入量的拉氏变换之比”。
原函数描述的系统:输入x i (t )⇒ 系统h (t )⇒ 输出x 0(t ) 以象函数描述的系统:输入X i (s )⇒ 系统G (s )⇒ 输出X 0(s )传递函数为:)()()(0s X S X s G i =传递函数是描述系统动态性能的数学模型的一种形式,是系统的复数域数学模型 二、传递函数的一般形式线性定常系统的运动微分方程式的一般形式为:imim m im inn n n x b x b x b x b x a x a x a x a ++++=++++---- 1)1(1)(01)1(01)(0......其中a 0、a 1。
a n ,b 0、b 1。
b m 均为实常数。
对上式做拉氏变换即可求得该系统的传递函数。
传递函数具有以下三种常用形式: ==)()()(0s X s X s G i nn n nmm m m a s a s a s a b s b sb sb ++++++++----11101110 (Ⅰ)型 ==)()()(0s X s X s G i ))...()(())...()((212100nma a ab b b s s s s s s a s s s s s s b ------ Ⅱ型==)()()(0s X s X s G i )12()1()12()1(2211122111++++++∏∏∏∏∏∏======s T sT s s s T sT s k al alal l all l l bl blbl l bll ll ζττζτνμλσρηⅢ其中,Ⅱ型中,s b1、s b2、s bm 是G (s )的零根,s a1、s a2、s an 是G (s )的极点,也是分母多项式的根。


控制工程基础董景新第四版简介《控制工程基础董景新第四版》是董景新教授所著的一本控制工程入门教材,通过全面介绍控制工程的基本概念、基本理论和基本方法,帮助读者建立起对控制工程的基础知识和基本技能的理解和掌握。
内容第一章:引言本章主要介绍控制工程的基本概念和发展历程,为后续章节的学习奠定基础。
首先对控制系统和控制工程的定义进行了阐述,并介绍了控制工程的主要任务和发展方向。
其次,对控制系统的分类进行了介绍,包括开环控制系统和闭环控制系统。
最后,介绍了控制系统的相关术语和符号,为后续章节的学习做好铺垫。
第二章:数学基础本章主要介绍控制工程所需要的数学基础知识。
首先介绍了常见的数学函数和符号,包括常用数学函数、求和符号、积分符号等。
其次,介绍了常用的数学运算法则,包括加法、乘法、指数运算等。
最后,介绍了常见的数学方程和常用的数学方法,包括线性方程组、矩阵运算、微积分等。
第三章:信号与系统本章主要介绍信号与系统的基本概念和分析方法。
首先介绍了信号的定义和分类,包括连续信号和离散信号、周期信号和非周期信号。
其次,介绍了信号的表示与分解方法,包括傅里叶级数和傅里叶变换。
最后,介绍了系统的定义和分类,包括线性系统和非线性系统、因果系统和非因果系统。
同时,介绍了系统的时域分析方法和频域分析方法。
第四章:传递函数与系统响应本章主要介绍传递函数和系统的响应特性。
首先介绍了传递函数的定义和性质,包括零极点分布和传递函数的单一性。
其次,介绍了系统的稳定性和系统的稳定判据,包括极点位置的判断和Nyquist判据。
最后,介绍了系统的时域响应和频域响应,包括单位冲击响应、单位阶跃响应、频率响应等。
第五章:控制系统的稳定性分析本章主要介绍控制系统的稳定性分析方法。
首先介绍了控制系统的稳定性的概念和判据,包括极点位置的判断和Nyquist稳定性判据。
其次,介绍了控制系统的根轨迹法和频率响应法,用于稳定性分析和设计。
最后,介绍了控制系统的相角裕度和增益裕度的概念和计算方法。


则系统闭环传递函数为假设得到的闭环传递函数三阶特征多项式可分解为令对应项系数相等,有二、高阶系统累试法对于固有传递函数是高于二阶的高阶系统,PID校正不可能作到全部闭环极点的任意配置。
但可以控制部分极点,以达到系统预期的性能指标。
根据相位裕量的定义,有则有则由式可独立地解出比例增益,而后一式包含两个未知参数和,不是唯一解。
通常由稳态误差要求,通过开环放大倍数,先确定积分增益,然后计算出微分增益。
同时通过数字仿真,反复试探,最后确定、和三个参数。
设单位反馈的受控对象的传递函数为试设计PID控制器,实现系统剪切频率,相角裕量。
解:由式,得由式,得输入引起的系统误差象函数表达式为令单位加速度输入的稳态误差,利用上式,可得试探法采用试探法,首先仅选择比例校正,使系统闭环后满足稳定性指标。
然后,在此基础上根据稳态误差要求加入适当参数的积分校正。
积分校正的加入往往使系统稳定裕量和快速性下降,此时再加入适当参数的微分校正,保证系统的稳定性和快速性。
以上过程通常需要循环试探几次,方能使系统闭环后达到理想的性能指标。
齐格勒-尼柯尔斯法(Ziegler and Nichols )对于受控对象比较复杂、数学模型难以建立的情况,在系统的设计和调试过程中,可以考虑借助实验方法,采用齐格勒-尼柯尔斯法对PID调节器进行设计。
用该方法系统实现所谓“四分之一衰减”响应(”quarter-decay”),即设计的调节器使系统闭环阶跃响应相临后一个周期的超调衰减为前一个周期的25%左右。
当开环受控对象阶跃响应没有超调,其响应曲线有如下图的S形状时,采用齐格勒-尼柯尔斯第一法设定PID参数。
对单位阶跃响应曲线上斜率最大的拐点作切线,得参数L 和T,则齐格勒-尼柯尔斯法参数设定如下:(a) 比例控制器:(b) 比例-积分控制器:,(c) 比例-积分-微分控制器:,对于低增益时稳定而高增益时不稳定会产生振荡发散的系统,采用齐格勒-尼柯尔斯第二法(即连续振荡法)设定参数。

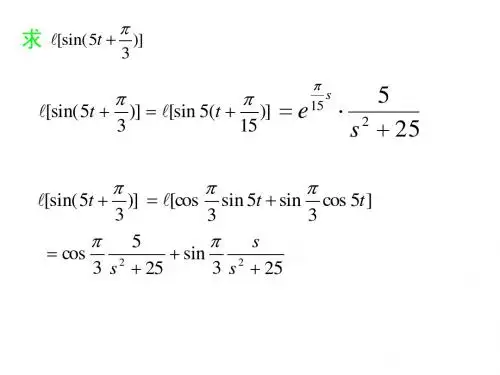

4-1 设单位反馈系统的开环传递函数为:10()1G s s =+。
当系统作用有下列输入信号时:()sin(30)r t t =+︒,试求系统的稳态输出。
解:系统的闭环传递函数为:10()()11()()1()111C s G s s R s G s Φ===++这是一个一阶系统。
系统增益为:1011K =,时间常数为:111T =其幅频特性为:()A ω=其相频特性为:()arctan T ϕωω=-当输入为()sin(30)r t t =+︒,即信号幅值为:1A =,信号频率为:1ω=,初始相角为:030ϕ=︒。
代入幅频特性和相频特性,有:1(1)A ====11(1)arctan arctan5.1911T ωϕω==-=-=-︒ 所以,系统的稳态输出为:[]()(1)sin 30(1)24.81)c t A A t t ϕ=⋅⋅+︒+=+︒4-2 已知系统的单位阶跃响应为:49()1 1.80.8(0)t t c t e e t --=-+≥。
试求系统的幅频特性和相频特性。
解:对输出表达式两边拉氏变换:1 1.80.8361()49(4)(9)(1)(1)49C s s s s s s s s s s =-+==++++++ 由于()()()C s s R s =Φ,且有1()R s s=(单位阶跃)。
所以系统的闭环传递函数为:1()(1)(1)49s s s Φ=++可知,这是由两个一阶环节构成的系统,时间常数分别为:1211,49T T ==系统的幅频特性为二个一阶环节幅频特性之积,相频特性为二个一阶环节相频特性之和:3-212()()()A A A ωωω===1212()()()arctan arctan arctanarctan49T T ωωϕωϕωϕωωω=+=--=--4-3 已知系统开环传递函数如下,试概略绘出奈氏图。
(1)1()10.01G s s=+(2)1()(10.1)G s s s =+(3))1008()1(1000)(2+++=s s s s s G (4)250(0.61)()(41)s G s s s +=+ 解:手工绘制奈氏图,只能做到概略绘制,很难做到精确。
控制系统传递函数控制系统是现代工程中广泛应用的重要技术之一,用于实现对各种工业过程和设备的自动控制。
而控制系统的核心是其传递函数,它能够描述输入和输出信号之间的关系。
本文将介绍控制系统传递函数的概念、用途以及一些常见的传递函数模型。
一、传递函数的定义与概念传递函数是用于描述控制系统输入和输出之间的关系的数学模型。
它是一个比较抽象的概念,通常用符号G(s)来表示。
其中,s是复变量,表示拉普拉斯变换的变量。
传递函数将输入信号X(s)转换为输出信号Y(s),通过设定传递函数来实现所需的控制效果。
传递函数一般可以写成如下形式:G(s) = Y(s) / X(s)其中,Y(s)是输出信号的拉普拉斯变换,X(s)是输入信号的拉普拉斯变换。
二、传递函数的用途传递函数在控制系统中起到了至关重要的作用。
它可以帮助工程师们分析和设计控制系统,理解系统的性能和行为。
1. 稳定性分析:传递函数能够帮助评估系统的稳定性。
通过分析传递函数的特征值或频率响应,可以判断系统是否稳定。
这对于控制系统的设计和优化非常重要。
2. 系统响应:传递函数可以描述系统对各种输入信号的响应特性。
通过分析传递函数的阶数、根的位置等信息,可以了解系统的响应速度、稳态误差和阻尼情况等。
3. 控制设计:传递函数可以用于控制器的设计。
通过选择合适的传递函数,可以实现对系统的精确控制,满足工程要求。
三、常见的传递函数模型控制系统传递函数可以采用不同的模型形式来描述不同的系统特性。
下面介绍几种常见的传递函数模型。
1. 一阶系统传递函数:G(s) = K / (Ts + 1)其中,K是传递函数的增益,T是一个时间常数。
这种传递函数常用于描述惯性系统,具有较简单的数学形式。
2. 二阶系统传递函数:G(s) = K / (τ^2s^2 + 2ζτs + 1)其中,K是传递函数的增益,τ是一个时间常数,ζ是阻尼系数。
这种传递函数用于描述振荡系统,可以较好地模拟实际工程中的许多系统。