(优选)控制工程基础第四章

3-18 N(s)=0时2222220()(11/)*(1/(1))/(11/(1)*1/)()[1()]*()[(1(1))/((1)1)]*()/(1)*()lim ()lim */(1)*(1/1/)0ssr s s s s s s s E s s R s s s s s s R s s s s R s e sE s s s s s s s ϕϕ→→=++++=-=++-+++=++==+++=R(S)=0时 /不受扰动的影响。

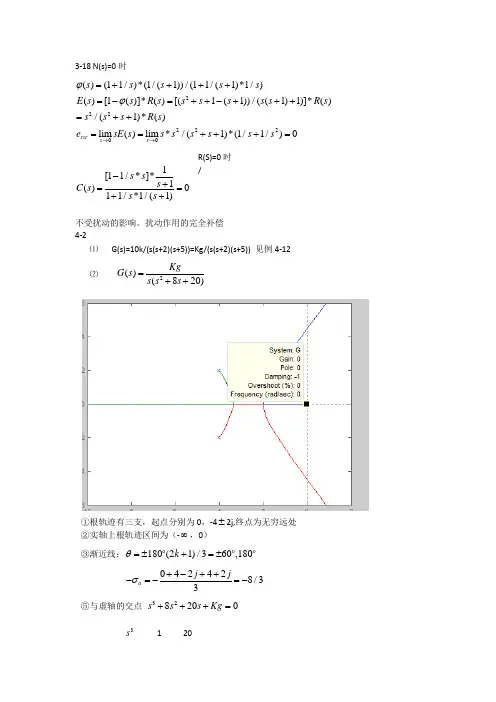
扰动作用的完全补偿 4-2⑴ G(s)=10k/(s(s+2)(s+5))=Kg/(s(s+2)(s+5)) 见例4-12 ⑵ 2()(820)KgG s s s s =++①根轨迹有三支，起点分别为0，-4±2j,终点为无穷远处 ②实轴上根轨迹区间为（-∞，0）③渐近线：180(21)/360,180k θ=±+=±042428/33a j jσ+-++-=-=-⑤与虚轴的交点 328200s s s Kg +++= 3s 1 201[11/*]*1()011/*1/(1)s s s C s s s -+==++2s 8 Kg S 20-Kg/8 0s Kg2s 的辅助方程 280s Kgp += 1.2s j j == ⑥出射角、入射角180(21)90157.48180263.563.5a k k θ=+--=--=-⑶G(s)=(1)(2)(5)Kgs s s s +++①根轨迹有4支，起点为0，-1，-2，-5，终点均在无穷远处 ②实轴上区间[-1 0].[-5 -2]③渐近线：180(21)/445,135k θ=±+=±±521024a δ+++-=-=-④分离点，会合点()N s =1, ()()()()D s s s 1s 2s 5=+++=43281710s s s +++s '()N s =0, 32'()4243410D s s s s =+++()'()'()()0N s D s N s D s -= 424243410s s s +++=0牛顿系数定理求：Kg=- ()()()s s 1s 2s 5+++dKg /ds = -(324243410s s s +++)记为P(s) 初选 s1=-0.5,-3.5,s-s1=s+0.5,s+3.5 用s+0.5,s+2.5去除p(s),Q(S)得12120.38R s s R =-=-同理2' 4.54s =- ⑤与虚轴的交点432817100s s s s Kg ++++=4s 1 17 Kg 3s 8 102s 17-5/4 Kg 10*0.5060Kg -= 19.75Kgp = S 10-0.506Kg 00s Kg辅助方程 215.80s Kgp += 1.2 1.12s j =± ⑷ ()(5)G s (1)(3)Kg s s s +=++根轨迹有2支，起点为-1，-3，终点为负无穷远处 实轴区间[-3 -1],[ -∞ -5]平面上的轨迹是圆，圆心为(-5,j0)处，圆半径为2.83 4-3 a 开环传递函数为21010(2)10(2)()*10(2)(2)10*(210)1**(2)k s s s s s s s G s s s s s k s k s k s s s ++===+++++++210()(210)10s s s k s ϕ=+++特征方程为2(210)10s s k s +++=0 用2210s s ++除特征方程得210*1210S sK s s =-++b 21010(1)(2)()(1)10210(1)1(1)(2)s s s s s s s s s s s τϕτττ++=+=++++++ 特征方程为 2210(1)s s s τ+++=0 210*1210ss s τ=-++根轨迹有2支，起点 1.22132s i -±==-±处，终点一支在零点0处，一支无限远处区间为[-∞0];分离点和会合点 ()10N s s= 2()210D s s s =++ '()10N s = '()22D s s =+210*(22)10(210)0s s s s +-++=得 1.2 3.16s ==±（3.16舍去）4-4 零点 -5 极点 0，-2 ±2ja 点(-1,j0) b(-1.5,j2) c(-6,j0) d(-4,j3) e(-1,j2.37) f(1,j1.5) a 点0(6565180)180s zi s pi ∠+-∠+=--+=-∑∑满足1544Kg ==b 点 30(012783)180-++=-满足0.5*4*2.11.103.8Kg ==C 点 180(180135135)0-+-=不满足条件 4-5 解：绘出g k 从0到无穷的根轨迹，如图所示：根轨迹有3支，起点为0，-4,-6，终点为无限远处 渐近线180(21)/360,180k θ=±+=±0461033a σ++-=-=- 分离点和会合点 32()1024D s s s s =++2'()32024D s s s =++ ()1N s = '()0N s = 由()*'()'()*()0D s N s D s N s -=得 1.2 1.57s =- -5.1（舍去）与虚轴的交点 用劳斯判据得 240g k p = 1.2s =%18%σ≤的要求，阻尼角60β≤ ，作P 60= 的径向直线交点为A,B 作为满足性能指标要求的闭环主导极点，1,2 1.2 2.1s j =-±（计算方法此点满足特征方程）|0|*||*||44g k A CA DA == /4*6 1.83g K k =≈44g k ≤ 1.83K ≤另一闭环极点为- 3(46 2.4)7.6s =-+-=-不影响系统的超调量，取 1.83K =即满足要求 4-6 (2)()(1)(4)k Kg s G s s s s +=++解：三支根轨迹：起点在0，-1，-4处，终点-2,与两支无限远处 实轴上区间[-1 0][-4 -2]处分离点和会合点()2N s s =+, 32()(1)(4)54D s s s s s s s =++=++ '()1N s = 2'()3104D s s s =++232(2)*(3104)(54)0s s s s s s +++-++=得10.6s =- 渐近线 01421.531σ++--=-=--180(21)/290,270k θ=+=与虚轴的交点 特征方程 3254(2)0g s s s k s ++++=3s 1 4+g k 2s 5 2g kS2035gk +0s 2S 行等于0 g k 是负值，无解，与虚轴不交 开环放大系数 K=g k *2/4=3 幅值条件1g k = 6g k = 3v k =设半径为r ，32(cos60sin60)5(cos60sin60)(4)(cos60sin60)20g g r r j r r j k r r j k -++-+++-++={r=2, g k =6,60β= 0.5ς= 16%δ=2wn =1.81p t s == 33.43*s t wnς==4-7 求分离点 ()1N s s =+ 232()()D s s s a s as =+=+ '()1N s = 2'()32D s s a s =+得s=0,1,2s =a>1时，若2(3)160a a +-> a>9时有2个分离点，a=9时有1个分离点且为-3，a<9无分离点a<1 无分离点4-8解：起点0，32j -±渐近线180(21)/360,180k θ=±+=±330222213a j j σ+++-=-=-与虚轴交点 用劳斯判据得 1,23s j =±027g k <<时系统稳定出射角180(21)(90125.3)35.3a k θ=+-+=-4-9 解 ⑴三支 起点为0，-2，终点为无穷远处 渐近线180(21)/360,180k θ=±+=±23a σ-=-系统不稳定⑵三支 起点为0，-2，终点一支为-3，两支为无穷远处 渐近线180(21)/290k θ=±+=±231312a σ--=-=- 系统仍不稳定⑶三支 起点为0，-2，终点一支为-1，两支为无穷远处 渐近线180(21)/290k θ=±+=±211312a σ--=-=-- 求分离点和会合点()1N s s =+ 232()(2)2D s s s s s =+=+'()1N s = 2'()34D s s s =+由()*'()'()*()0D s N s D s N s -=得10,,22s s s ==-=-无分离点 系统稳定 20c z -<-<时，系统稳定4-10内环特征方程为：2200Ts s ++= 2*120s T s =-+作根轨迹，两个零点为原点，极点一个为无穷远处，一个为-20。

《控制工程基础》电子教案第一章：绪论1.1 课程介绍解释控制工程的定义强调控制工程在工程学中的重要性概述课程的目标和内容1.2 控制系统的基本概念介绍控制系统的定义解释控制系统的组成部分讨论控制系统的分类和特点1.3 控制理论的发展历程简述控制理论的发展历程强调现代控制理论的重要性第二章：数学基础2.1 线性代数基础介绍矩阵和向量的基本运算解释行列式和逆矩阵的概念讨论矩阵的秩和特征值2.2 微积分基础复习微积分的基本概念介绍导数和微分方程的概念讨论积分的概念和方法2.3 离散时间系统介绍离散时间系统的定义解释离散时间系统的差分方程讨论离散时间系统的性质和特点第三章：连续时间系统3.1 连续时间系统的描述方法介绍连续时间系统的微分方程描述解释状态空间描述的方法讨论两种描述方法的关系和转换3.2 连续时间系统的稳定性介绍连续时间系统的稳定性概念解释李雅普诺夫稳定性的判断方法讨论稳定性条件和不稳定性的原因3.3 连续时间系统的时域分析介绍连续时间系统的时域分析方法解释零输入响应和零状态响应的概念讨论时域分析的应用和意义第四章：离散时间系统4.1 离散时间系统的描述方法介绍离散时间系统的差分方程描述解释离散时间系统的状态空间描述讨论两种描述方法的关系和转换4.2 离散时间系统的稳定性介绍离散时间系统的稳定性概念解释离散时间系统的稳定性条件讨论稳定性判断方法和不稳定性的原因4.3 离散时间系统的时域分析介绍离散时间系统的时域分析方法解释离散时间系统的零输入响应和零状态响应讨论时域分析的应用和意义第五章：控制器设计5.1 概述控制器设计的目标和方法解释控制器设计的目标介绍常见的控制器设计方法5.2 PID控制器设计解释PID控制器的作用和原理介绍PID控制器的参数调整方法讨论PID控制器的应用和优点5.3 状态反馈控制器设计介绍状态反馈控制器的作用和原理解释状态反馈控制器的设计方法讨论状态反馈控制器的优点和应用第六章：频域分析6.1 频率响应分析介绍频率响应的概念和重要性解释传递函数和频率响应之间的关系讨论频率响应分析的方法和步骤6.2 传递函数的性质介绍传递函数的定义和基本性质解释传递函数的零点和极点讨论传递函数的稳定性和频率特性6.3 频域设计方法介绍频域设计方法的概念和原理解释截止频率和滤波器设计的要求讨论常用频域设计工具和技术第七章：频域设计实例7.1 低通滤波器设计介绍低通滤波器的作用和应用解释低通滤波器的设计方法和步骤讨论低通滤波器的性能指标和选择7.2 高通滤波器设计介绍高通滤波器的作用和应用解释高通滤波器的设计方法和步骤讨论高通滤波器的性能指标和选择7.3 其他类型滤波器设计介绍带通滤波器和带阻滤波器的作用和应用解释带通滤波器和带阻滤波器的设计方法讨论不同类型滤波器的性能指标和选择第八章：状态空间分析8.1 状态空间表示介绍状态空间的概念和表示方法解释状态空间矩阵和状态方程讨论状态空间表示的优点和应用8.2 状态空间稳定性和可控性介绍状态空间稳定性和可控性的概念解释李雅普诺夫稳定性和李雅普诺夫可行域讨论状态空间稳定性和可控性的判定方法8.3 状态空间最优控制介绍状态空间最优控制的概念和原理解释哈密顿-雅可比方程和解法讨论状态空间最优控制的应用和实现方法第九章：非线性控制9.1 非线性系统的定义和特点介绍非线性系统的定义和特点解释非线性系统的常见类型和行为讨论非线性系统分析和设计的方法和挑战9.2 非线性控制器设计介绍非线性控制器的设计方法和工具解释非线性PID控制器和滑模控制器的设计讨论非线性控制器的应用和效果9.3 非线性控制的应用实例介绍非线性控制在实际系统中的应用实例解释非线性控制在控制和航空航天领域的应用讨论非线性控制的优势和局限性第十章：控制系统仿真10.1 控制系统仿真概述介绍控制系统仿真的概念和重要性解释控制系统仿真的方法和工具讨论控制系统仿真的优点和局限性10.2 MATLAB控制系统仿真介绍MATLAB控制系统仿真的基本方法解释MATLAB中的仿真工具和函数讨论MATLAB控制系统仿真的应用和示例10.3 实际系统仿真案例分析介绍实际系统仿真案例的分析和实现方法解释实际系统仿真案例的仿真结果和分析讨论实际系统仿真案例的启示和应用前景第十一章：现代控制理论11.1 概述现代控制理论介绍现代控制理论的发展背景和意义解释现代控制理论的基本概念和原理讨论现代控制理论在工程应用中的重要性11.2 线性二次调节器（LQR）解释线性二次调节器的定义和特点介绍LQR控制器的设计方法和步骤讨论LQR控制器的性能分析和应用实例11.3 鲁棒控制理论介绍鲁棒控制的定义和目的解释鲁棒控制的设计方法和原理讨论鲁棒控制在系统不确定性和外部干扰下的性能第十二章：自适应控制12.1 概述自适应控制介绍自适应控制的概念和需求解释自适应控制的目标和原理讨论自适应控制在系统和环境变化中的应用12.2 自适应控制器设计介绍自适应控制器的设计方法和算法解释自适应控制器的自适应律和调整机制讨论自适应控制器的性能分析和应用实例12.3 自适应控制的应用介绍自适应控制在工业和农业领域的应用实例解释自适应控制在导航和飞行控制系统中的应用讨论自适应控制的优势和挑战第十三章：数字控制13.1 概述数字控制介绍数字控制的概念和与模拟控制的比较解释数字控制系统的组成和特点讨论数字控制在现代控制系统中的应用13.2 数字控制器设计介绍数字控制器的设计方法和算法解释数字控制器的离散化和实现方式讨论数字控制器的性能分析和优化方法13.3 数字控制的应用实例介绍数字控制在工业和家庭领域的应用实例解释数字控制在智能家居和工业自动化系统中的应用讨论数字控制的优势和局限性第十四章：控制系统实验14.1 控制系统实验概述介绍控制系统实验的目的和重要性解释控制系统实验的步骤和注意事项讨论控制系统实验在教学和研究中的应用14.2 实验设备和工具介绍控制系统实验中常用的设备和工具解释各种设备和工具的功能和操作方法讨论实验设备的选用和维护14.3 实验项目和解题方法介绍控制系统实验的项目和目标解释实验的解题方法和步骤讨论实验结果的分析和讨论第十五章：控制系统综合与应用15.1 控制系统综合概述介绍控制系统综合的目标和意义解释控制系统综合的方法和步骤讨论控制系统综合在实际应用中的挑战和解决方案15.2 控制系统应用实例介绍控制系统在工业和航空航天领域的应用实例解释控制系统在智能交通和智能中的应用讨论控制系统应用的挑战和发展方向15.3 控制系统未来的发展趋势探讨控制系统未来的发展趋势和机遇分析控制系统的创新技术和算法讨论控制系统在可持续发展和绿色能源领域的应用前景重点和难点解析本文档详细地介绍了《控制工程基础》这门课程的电子教案，内容涵盖了连续时间系统、离散时间系统、控制系统的基本概念、数学基础、控制器设计、频域分析、状态空间分析、非线性控制、仿真技术、现代控制理论、自适应控制、数字控制、实验项目和综合应用等多个方面。

2007机械工程控制基础第四章习题答案第4章频率特性分析4.1什么是系统的频率特性？答：对于线性系统，若输入为谐波函数， 则其稳态输出一定是同频率的谐波函数，将输出的幅值与输入的幅值之比定义为系统的幅频特性，将输出的相位之差定义为系统的相频特性。

系统的幅频特性和相频特性简称为系统的频率特性。

4.4若系统输入为不同频率-■的正弦Asin •，其稳态输出相应为 Bsin(，，t •「)。

求该系统 的频率特性。

解：由系统频率特性的定义知： G(i H-e j ：A4.5已知系统的单位阶跃响应为 X o (t) = 1 -1.8e^t0.8e° (t _ 0)，试求系统的幅频特性与相频特性。

解：由已知条件得： Xi(s)= —， X o (s)二—- —80 8sss+4s+9得系统传函为：G (s)二匹◎36——X i (s) (s + 4)(s+9)G(j ■)得系统频率特性:G(j ■)36 (4 j ■ )(9 j )，其中幅频特性为:A(^) = G( j ®)| =36相频特性为： ：C •) = -arctanarctan — 4 94.6由质量、弹簧、阻尼组成的机械系统如图( 4.6)所示。

已知m=1kg ，k 为弹簧刚度，c 为阻尼系数。

若外力 f (t) =2sin2tN ，由实验得到系统稳态响应为xoss试确定k 和C 。

解：由系统结构知系统的动力学方程为:mx o (t) cx °(t) 伙⑴工 f (t)当m=1时，得系统传函为：1G(s)二二 ，得系统频率特性为:s + cs + kJ VZ/7/图(题4.6)其中，幅频特性为 G(j )，相频特性为:(■)J (k _(c 2)2+c 2们2解得 k =4 , c =1。

试求系统的稳态输出。

(1) x i (t)二 sin(t 30°)X oss1 (t) = -4^S in (t +300—5.20)V1224.11已知系统传递函数方框图如图所示，现作用于系统输入信号 的稳态响应。

《控制工程基础》电子教案第一章：绪论1.1 课程介绍了解控制工程基础的课程背景、目的和意义熟悉课程的结构和内容安排1.2 控制理论的基本概念定义控制、控制系统和控制理论掌握系统、输入、输出、反馈等基本术语1.3 控制工程的应用领域了解控制工程在工程、工业和科学研究中的应用认识控制工程在自动化、技术、航空航天等领域的案例第二章：数学基础2.1 函数、极限和连续性学习函数的概念、性质和分类掌握极限的定义和计算方法理解函数的连续性和间断性2.2 微分和积分学习导数的概念、计算规则和应用掌握积分的概念、计算方法和应用2.3 常微分方程了解常微分方程的定义和分类学习常微分方程的解法和解的存在性第三章：线性系统的时域分析3.1 系统的数学模型了解系统的输入、输出和状态变量学习线性时不变系统的数学模型3.2 系统的零输入响应和零状态响应掌握零输入响应和零状态响应的概念和计算方法分析系统的稳定性、收敛性和瞬态特性3.3 系统的稳态性能分析学习稳态误差的定义和计算方法分析系统的稳态误差性能和稳态精度第四章：线性系统的频域分析4.1 频率响应的概念了解频率响应的定义和意义学习频率响应的计算和表示方法4.2 系统的频率特性掌握频率特性的概念和性质分析系统的幅频特性和相频特性4.3 系统的稳定性分析学习奈奎斯特稳定性和波特-瓦诺夫定理分析系统的稳定性条件和稳定裕度第五章：数字控制系统5.1 数字控制系统的组成了解数字控制系统的硬件和软件结构学习数字控制器的实现方法和算法5.2 数字控制器的设计方法掌握PID控制器和模糊控制器的原理和方法学习数字控制器设计的步骤和注意事项5.3 数字控制系统的仿真和实验学习数字控制系统的仿真工具和实验设备进行数字控制系统的仿真实验和实际系统测试第六章：线性系统的状态空间分析6.1 状态空间模型的概念了解状态空间模型的定义和表示方法学习状态空间模型的转换关系和坐标变换6.2 状态空间方程的求解掌握状态方程和输出方程的求解方法分析系统的零输入响应和零状态响应6.3 状态空间分析的应用学习状态空间方法在系统控制和稳定性分析中的应用掌握状态反馈控制和观测器设计的基本原理第七章：非线性控制系统7.1 非线性系统的特点了解非线性系统的定义和特点学习非线性系统建模和分析的方法7.2 非线性控制理论掌握非线性控制系统的数学模型和稳定性分析学习非线性控制算法和设计方法7.3 非线性控制的应用了解非线性控制在、航空航天等领域的应用案例分析非线性控制系统的仿真和实验结果第八章：鲁棒控制系统8.1 鲁棒控制的概念了解鲁棒控制的定义和意义学习鲁棒控制的目标和设计方法8.2 鲁棒控制理论掌握鲁棒控制系统的数学模型和稳定性分析学习鲁棒控制算法和设计方法8.3 鲁棒控制的应用了解鲁棒控制在工业和航空航天等领域的应用案例分析鲁棒控制系统的仿真和实验结果第九章：智能控制系统9.1 智能控制的基本概念了解智能控制的定义、发展和应用领域学习智能控制系统的结构和特点9.2 人工神经网络和模糊控制掌握人工神经网络的基本原理和应用学习模糊控制的基本原理和设计方法9.3 智能控制系统的应用了解智能控制在、自动化和工业等领域的应用案例分析智能控制系统的仿真和实验结果第十章：控制系统的设计与实践10.1 控制系统的设计流程学习控制系统设计的基本流程和方法掌握控制系统设计中的注意事项和技术要求10.2 控制系统的仿真与实验学习控制系统仿真的方法和工具进行控制系统的实验设计和实验数据分析10.3 控制系统的设计案例分析分析典型的控制系统设计案例学习控制系统设计中的创新和实践经验重点和难点解析重点一：控制理论的基本概念补充说明：控制系统是工程和科学中的一个核心概念，理解其基本组成部分对于深入学习控制理论至关重要。

第四章 系统的时间响应分析内容提要一、时间响应的组成任一稳定系统的时间响应都是由瞬态响应和稳态响应两部分组成。

系统的时间响应可从两方面分类，按振动性质可分为自由响应与强迫响应，按振动来源可分为零输入响应与零状态响应。

控制工程所要研究的响应往往是零状态响应。

二、时域性能指标1.延迟时间d t2.上升时间r t21ξωβπωβπ--=-=n d r t 3.峰值时间p t21ξωπωπ-=n d p t ＝4.调节时间s t一阶系统 ⎩⎨⎧=∆==∆=)05.0 (3)02.0 (4T t T t s s二阶系统 ⎪⎪⎩⎪⎪⎨⎧=∆==∆=)05.0 ( 3)02.0 ( 4n sns t t ξωξω5.最大超调量p M%10021⨯=--ξξπeM p6.稳态误差ss e三、稳定性1.稳定性的概念线性系统稳定的充分必要条件为：系统特征方程的全部根都具有负实部。

又由于系统特征方程的根就是系统的极点，所以系统稳定的充分必要条件就是系统的全部极点都在s 平面的左半平面。

2.劳斯稳定判据劳斯判据指出系统稳定的充分必要条件是：劳斯表中第一列元素全部大于零。

若出现小于零的元素，系统不稳定，且第一列元素符号改变的次数等于系统特征方程具有正实部特征根的个数。

四、稳态偏差1.参考输入作用下系统的稳态偏差0lim ()lim()1()()ss s s ss E s R s G s H s ε→→=⋅=+2.干扰作用下系统的稳态误差)()()()(1)(lim)(lim 21200S N s H s G s G s sG s E s e s s ss N +-=⋅=→→图4-1 参考输入作用下系统方框图图4-2 干扰作用下的反馈系统方框图4-1 什么是时间响应？时间响应由哪两部分组成？各部分的定义是什么？答：系统在外加作用(输入)激励下，其输出量随时间变化的函数关系称之为系统的时间响应，通过对时间响应的分析可揭示系统本身的动态特性。

4-1设单位反应系统的开环传达函数为：G (s)10。

当系统作用有以下输入信号时：r (t ) sin(t 30 ) ，试s1求系统的稳态输出。

解：C( s)G( s)10系统的闭环传达函数为：( s)11R(s)1G(s)s111这是一个一阶系统。

系统增益为：K 101，时间常数为： T 1111其幅频特征为：A()K12T 2其相频特征为：()arctan T当输入为 r (t )sin(t30 ) ，即信号幅值为：A 1 ，信号频次为：1，初始相角为：030。

代入幅频特征和相频特征，有：K10 1110A(1)2T 2 1 112122111(1)arctan T1所以，系统的稳态输出为：arctan15.1911c(t ) A(1) A sin t30(1)10sin(t24.81 )1224-2 已知系统的单位阶跃响应为：c(t) 1 1.8e 4t0.8e 9t(t0) 。

试求系统的幅频特征和相频特征。

解：对输出表达式两边拉氏变换：C( s)1 1.80.8361s s 4s9s( s4)(s9)s s1)s(1)(49因为 C ( s)(s)R( s) ，且有R(s)1（单位阶跃）。

所以系统的闭环传达函数为：s( s)1( s 1)(s1) 4 9可知，这是由两个一阶环节构成的系统，时间常数分别为：T 1 , T 1 14 2 9系统的幅频特征为二个一阶环节幅频特征之积，相频特征为二个一阶环节相频特征之和：A( ) A 1( )A 2( )11 12T 1212T 222 21)(1)(18116( )1() 2()arctan T 1 arctan T 2arctan4arctan94-3 已知系统开环传达函数以下，试大要绘出奈氏图。

1（ 1） G ( s)（ 2） G ( s)1 0.01s1s(1 0.1s)1000(s 1) （ 3） G ( s)s(s 2 8s 100)50(0.6 s 1) （ 4） G ( s)s 2 (4 s 1)解：手工绘制奈氏图，只好做到大要绘制，很难做到精准。