语音信号的频域分析

实验二语音信号的频域特性一、实验目的（1）结合汉语语音信号的各类音素和复元音的特点分析其频域性质；（2）熟悉语音信号的各类音素和复元音的频域参数；（3）熟悉声音编辑软件PRAAT的简单使用和操作。

二、实验记录与思考题1. 观察语音信号的频域特点，总结其规律。

浊音段：其谱线结构是与浊音信号中的周期信号密切相关。

具有与基音及其谐波对应的谱线。

频谱包络中有几个凸起点，与声道的谐振频率相对应。

这些凸起点为共振峰。

清音段：清音的频谱无明显的规律，比较平坦。

2.总结清音/b/p/m/f/d/t/n/l/g/k/h/j/q/x/z/c/s/zh/ch/sh/r/共21个的语谱图的规律，给出辅音的能量集中区；语谱图中的花纹有横杠、乱纹和竖直条。

横杠是与时间轴平行的几条深黑色带纹，它们是共振峰。

从横杠对应的频率和宽度可以确定相应的共振峰频率和带宽。

在一个语音段的语谱图中，有没有横杠出现是判断它是否是浊音的重要标志。

竖直条是语谱图中出现于时间轴垂直的一条窄黑条。

每个竖直条相当于一个基音，条纹的起点相当于声门脉冲的起点，条纹之间的距离表示基音周期，条纹越密表示基音频率越高。

b，p……清音的语谱图为乱纹。

辅音的能量集中区为：高频区3. 总结浊音/a/o/e/i/u/ü/ao/ai/ei/ou/ie /an/en/in/ang/eng/ong/ing/共18个的语谱图的规律，提取这18个浊音的基频、前三个共振峰频率4./r/、/m/、/n/、/l/ 从这几个音素的的基频、共振峰频率5.分析宽带语谱图和窄带语谱图的不同之处，请解释原因；语谱图中的花纹有横杠、乱纹和竖直条等。

横杠是与时间轴平行的几条深黑色带纹，它们是共振峰。

从横杠对应的频率和宽度可以确定相应的共振峰频率和带宽。

在一个语音段的语谱图中，有没有横杠出现是判断它是否是浊音的重要标志。

竖直条（又叫冲直条）是语谱图中出现与时间轴垂直的一条窄黑条。

每个竖直条相当于一个基音，条纹的起点相当于声门脉冲的起点，条纹之间的距离表示基音周期。

《信号与系统》大作业语音信号的采集与频谱分析——基于Matlab的语音信号处理学生姓名：学号：专业班级：电子工程学院卓越班指导老师：2015年6月22日摘要本设计用苹果手机自带的录音设备采集了原始语音，并导入了电脑转成wav格式，然后用MATLAB和Adobe audition对其进行时域分析。

接着利用傅里叶变换进行了频域分析，绘制频谱图，再录制一段加上歌曲的伴奏的语音与原唱进行了对比分析，得出了我与歌星在频域上的差别。

本设计给信号加了两种噪声并通过观察加噪后的频谱和试听回放效果比较加噪前后的差别，最后，设计了FIR数字低通滤波器和带通滤波器，分析滤波前后的频谱。

再次试听回放效果，得出结论。

关键词：语音、FFT、频谱图、噪声、滤波器AbstractThis design is based on the general function of Matlab and Adobe edition to deal with Audio signals. The original signals are collected by iPhone’s built-in recording equipment.First，I compare the file generated by myself with that of thesame song sang by a famous singer.The emphasis is generally laid on analysing the difference in frequncy domain,but time domain will be included too.After that,two noise signals are added to the original signal respectively and let them pass a filter to analyse it.In the two process mentioned before,I make comparison between the before and after frequency domain.Sampling Theorem is the base of my design.It is by sampling we can get discrete signals from the original one and draw the image in time domain.Also,fast fourier transform is employed(FFT)to get the signals in frequency domain.The ayalysis of frequency domain is the highlight of this design.Through this design,I can deepen my comprehension of principles of audio signals and I have learnt how to deal with it.Through met with much hindrance,I improved my skills finally.Keywords： audio signal、TTT、noise、filter1 绪论1.1课题的研究意义语音信号处理属于信息科学的一个重要分支，它是研究用数字信号处理技术对语音信号进行处理的一门新兴学科，同时又是综合性的多学科领域和涉及面很广的交叉学科，因此我们进行语言信号处理具有时代的意义。

语音信号时域和频域通俗理解语音信号是一种广泛使用的信号类型，它包含了人类声音的各种特征。

在理解语音信号时域和频域的表现时，首先需要理解这两个概念的基本含义。

时域：在时间域中，信号是按照时间顺序排列的一组值。

对于语音信号，每一帧或每个样本点都代表了声音在不同时刻的强度或幅度。

在语音信号处理中，时域分析通常涉及对这些样本点进行各种操作，如加权、过滤、卷积等。

时域分析可以揭示信号的瞬态特性，如声音的起始和结束，但其对频率成分的敏感性较低。

频域：在频域中，信号被转换成了频率成分的形式。

这意味着我们将信号分解为一系列不同频率的分量，每个分量都有其特定的幅度和相位。

在语音信号中，这些频率成分反映了声音的各个部分（如基频、谐波等）如何由不同的振动模式产生。

频域分析提供了对信号的全面理解，因为它能够揭示信号的能量如何分布在不同的频率上。

现在，让我们更深入地理解语音信号在时域和频域的表现：时域中的语音：当我们说话时，我们的声带会振动并产生声音。

这些振动会产生一系列的样本点，这些点在时间上按顺序排列。

如果我们观察这些样本点，我们可能会注意到声音的起始和结束，以及一些明显的变化。

但是，如果我们想了解更多关于声音的内容，比如它的基频或谐波结构，我们需要在频域中进行分析。

频域中的语音：当我们观察语音信号的频谱时，我们会看到一系列的频率成分。

这些成分可以代表基频、谐波以及其他声音特征。

例如，如果一个声音的主要成分是基频，那么我们可能会看到一个明显的峰值在低频区域。

如果一个声音包含多个谐波，我们可能会看到一系列更高或更低的频率成分。

了解这些频率成分可以帮助我们更好地理解声音的特征，比如音调、音量等。

总之，理解语音信号时域和频域的表现对于语音处理和通信等领域非常重要。

在时域中，我们关注声音的瞬态特性；而在频域中，我们关注声音的频率成分。

通过将信号从一种表示转换到另一种表示，我们可以更全面地了解和处理语音信号。

第一章引言语音信号是一种非平稳的时变信号，它携带着各种信息。

在语音编码、语音合成、语音识别和语音增强等语音处理中无一例外需要提取语音中包含的各种信息。

语音信号分析的目的就在与方便有效的提取并表示语音信号所携带的信息。

语音信号分析可以分为时域和频域等处理方法。

语音信号可以认为在短时间内(一般认为在 10~30ms 的短时间内)近似不变，因而可以将其看作是一个准稳态过程, 即语音信号具有短时平稳性。

任何语音信号的分析和处理必须建立在“短时”的基础上, 即进行“短时分析”。

时域分析:直接对语音信号的时域波形进行分析，提取的特征参数有短时能量，短时平均过零率，短时自相关函数等。

频域分析:对语音信号采样，并进行傅里叶变换来进行频域分析。

主要分析的特征参数：短时谱、倒谱、语谱图等。

本文采集作者的声音信号为基本的原始信号。

对语音信号进行时频域分析后，进行加白噪声处理并进行了相关分析，设计滤波器并运用所设计的滤波器对加噪信号进行滤波, 绘制滤波后信号的时域波形和频谱。

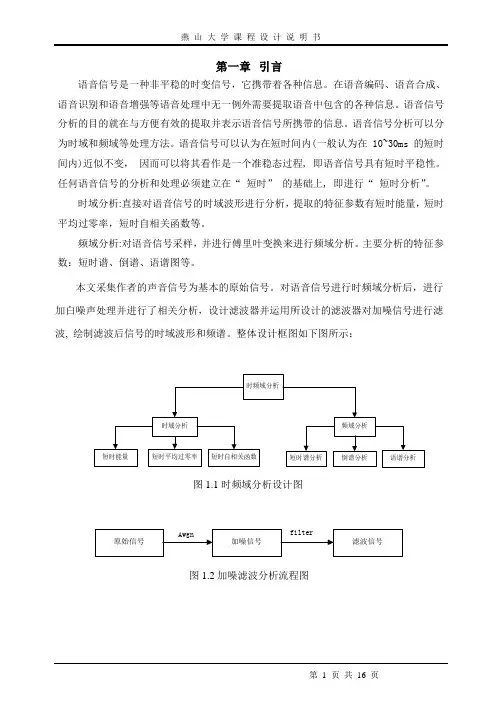
整体设计框图如下图所示：图1.1时频域分析设计图图1.2加噪滤波分析流程图第二章 语音信号时域分析语音信号的时域分析可直接对语音信号进行时域波形分析，在此只只针对语音信号的短时能量、短时平均过零率、短时自相关函数进行讨论。

2.1窗口选择由人类的发生机理可知，语音信号具有短时平稳性，因此在分析讨论中需要对语音信号进行加窗处理进而保证每个短时语音长度为10~30ms 。

通常选择矩形窗和哈明窗能得到较理想的“短时分析”设计要求。

两种窗函数的时域波形如下图2.1所示：samplew （n ）samplew （n ）图2.1 矩形窗和Hamming 窗的时域波形矩形窗的定义：一个N 点的矩形窗函数定义为如下{1,00,()n Nw n ≤<=其他（2.1）哈明窗的定义：一个N 点的哈明窗函数定义为如下0.540.46cos(2),010,()n n NN w n π-≤<-⎧⎨⎩其他= （2.2）这两种窗函数都有低通特性，通过分析这两种窗的频率响应幅度特性可以发现（如图2.2）：矩形窗的主瓣宽度小（4*pi/N ），具有较高的频率分辨率，旁瓣峰值大（-13.3dB ），会导致泄漏现象；哈明窗的主瓣宽8*pi/N ，旁瓣峰值低（-42.7dB ），可以有效的克服泄漏现象，具有更平滑的低通特性。

语音信号采样和频谱分析一．实验目的1掌握傅里叶变换的物理意义,深刻理解傅里叶变换的内涵；2了解MATLAB对声音信号的处理指令；3了解计算机存储信号的方式及语音信号的特点；4加深对采样定理的理解；5加深学生对信号分析工程应用的理解,拓展学生在信号分析领域的综合应用能力;二．实验内容本实验利用MATLAB指令录制一段语音信号,观察其时域波形并进行傅里叶变换,观察其频域的频谱;根据该信号的频谱构成,选择三种不同的采样频率重新录制该语音信号,并试听回放效果,进行比较,以验证采样定理,并了解MATLAB对声音信号的处理指令,加深对采样定理的理解;关键词：傅里叶变换信号采样三、实验原理语音信号是一种连续变化的模拟信号,而计算机只能处理和记录二进制的数字信号,因此,由自然音而得的音频信号必须用计算机的声音编辑工具,先进行语音采样,然后利用了计算机上的A/D转换器,将模拟的声音信号变成离散的量化了的数字信号量化和编码,变成二进制数据后才能送到计算机进行再编辑和存储;语音信号输出时,量化了的数字信号又通过D/A转换器,把保存起来的数字数据恢复成原来的模拟的语音信号;1应用MATLAB 进行声音的录制 2应用MATLAB 进行声音的播放 3语音信号的频谱分析 ;傅里叶变换建立了信号频谱的概念;所谓傅里叶分析即分析信号的频谱频率构成、频带宽度等;对语音信号的分析也不例外,也必须采用傅里叶变换这一工具; 对于连续时间信号)(t f ,其傅里叶变换)(ωF 为：⎰∞∞--=dt e t f F t j ωω)()( 四、实验任务1应用MATLAB 进行声音的录制在MATLAB 命令窗口中键入“y=wavrecord8000,8000,1”,并按回车键,此时刻以后的18000/8000秒时段内的声音信号将以y 为文件名,以数字声音信号.wav 格式存储在MATLAB 的工作空间里;纪录长度为80000,采样频率为8000Hz,声道数为1;图为录制的语音：“信号与系统”;2应用MATLAB 进行声音的播放在MATLAB 命令窗口中键入“soundy,Fs ”,按下回车键就能听到回放的声音;当Fs=8000时,听到的是原来未失真的声音；当Fs=6000时,听到的声音比较低沉；当Fs=10000时,听到的声音很尖锐;3语音信号的频谱分析在MATLAB 命令窗口中键入“p=ffty;plotabsp ”按下回车键后出现如图所示图形： 从图中可以看出该音频的上限频率为4000Hz;4采样定理一个频谱受限的信号ft,如果频谱只占据m m ωω+-~的范围,则信号)(t f 可以用等间隔的抽样值唯一地表示;而抽样间隔必须不大于mf 21其中m m f ⋅=πω2,或者说,最低抽样频率为m f 2;低抽样频率为m f 2;该实验中,音频的上限频率为4000Hz,所以采用的抽样信号的频率为该频率的两倍8000Hz;当采用小于8000Hz 的频率抽样时,回放声音低沉；当采用大于8000Hz的频率采样时,回放声音尖锐; 结论：本次试验是进行语音信号的采集和频谱分析,实验纪录了长度为80000,采样频率为8000Hz采样一段音频,并进行频谱分析,最终经过分析得只有以两倍上限频率回放音频时才会得到原音频信号,否则都会失真;本次试验不仅学习到了新知识,而且复习到了抽样定理的许多内容,加深了对这些内容的理解,受益很多。

基于MATLAB 分析语音信号时域特征钱平（信号与信息处理 s101904010）一、频域特征实验原理1、短时傅立叶变换由于语音信号是短时平稳的随机信号，某一语音信号帧的短时傅立叶变换的定义为：()()()ee Xmj m j nm n w m x ωω-∞-∞=∑-=其中w(n-m)是实窗口函数序列，n 表示某一语音信号帧。

令n-m=k'，则得到()()()()ek k e Xk n j k j nn x w--∞-∞=∑-=ωω,,于是可以得到)()()eeeX kj k mj j nk n x k w ωωω-∞-∞=-∑-=假定()()()∑∞-∞=-=k kj j nee Xk n x k w ωω则可以得到()()e Xee Xj nnj j nωωω-=同样，不同的窗口函数，将得到不同的傅立叶变换式的结果。

由上式可见，短时傅立叶变换有两个变量：n 和ω，所以它既是时序n 的离散函数，又是角频率ω的连续函数。

与离散傅立叶变换逼近傅立叶变换一样，如令ω=2πk/N ，则得离散的短时傅立叶吧如下：()()()()()10,/2/2-≤≤-==∑∞-∞=-N k m n w m x k m Nm j nNnk j ne XeXπ2、语谱图水平方向是时间轴，垂直方向是频率轴，图上的灰度条纹代表各个时刻的语音短时谱。

语谱图反映了语音信号的动态频率特性，在语音分析中具有重要的实用价值。

被成为可视语言。

语谱图的时间分辨率和频率分辨率是由窗函数的特性决定的。

时间分辨率高，可以看出时间波形的每个周期及共振峰随时间的变化，但频率分辨率低，不足以分辨由于激励所形成的细微结构，称为宽带语谱图；而窄带语谱图正好与之相反。

宽带语谱图可以获得较高的时间分辨率，反映频谱的快速时变过程；窄带语谱图可以获得较高的频率分辨率，反映频谱的精细结构。

两者相结合，可以提供带两与语音特性相关的信息。

语谱图上因其不同的灰度，形成不同的纹路，称之为“声纹”。