下载文档原格式
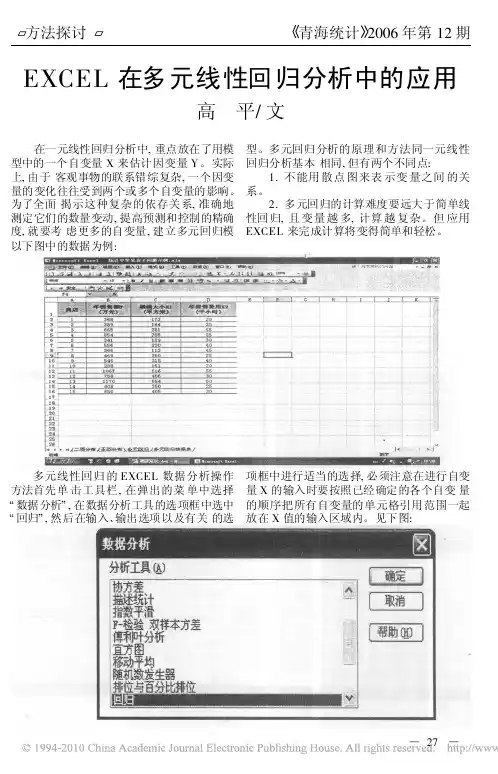
EXCEL 在多元线性回归分析中的应用高 平/文在一元线性回归分析中,重点放在了用模型中的一个自变量X 来估计因变量Y 。
实际上,由于客观事物的联系错综复杂,一个因变量的变化往往受到两个或多个自变量的影响。
为了全面揭示这种复杂的依存关系,准确地测定它们的数量变动,提高预测和控制的精确度,就要考虑更多的自变量,建立多元回归模型。
多元回归分析的原理和方法同一元线性回归分析基本相同,但有两个不同点:1.不能用散点图来表示变量之间的关系。
2.多元回归的计算难度要远大于简单线性回归,且变量越多,计算越复杂。
但应用EXCEL 来完成计算将变得简单和轻松。
以下图中的数据为例: 多元线性回归的EXCEL 数据分析操作方法首先单击工具栏,在弹出的菜单中选择数据分析 ,在数据分析工具的选项框中选中 回归 ,然后在输入、输出选项以及有关的选项框中进行适当的选择,必须注意在进行自变量X 的输入时要按照已经确定的各个自变量的顺序把所有自变量的单元格引用范围一起放在X 值的输入区域内。
见下图:!27!点击 确定按钮,即可得到线性回归分析的结果。
见下图:!!28根据上图中的显示结果,可直接写出二元线性回归方程:Y i=b0+b1X1i+b2X2i=-51.3127+1. 4053x1i+6.3823x2ib1表示在促销费用固定时,商店的规模大小每增加1平方米,年销售额平均增加1.4053万元;b2表示在商店的规模大小固定时,促销费用每增加1万元,年销售额平均增加6.3823万元。
这里b1即商店的规模大小的回归系数比一元线性回归方程中的回归系数b= 1.6246小,是因为一元线性回归方程只考虑了商店的规模大小对年销售额的影响,忽略了促销费用这一很重要的因素,在商店的规模大小的影响中渗入了促销费用的影响。
这里的截距b0=-51.3127万元,与一元线性回归方程中的截距+99.01万元有很大的不同,因为X1=0和X2 =0都不在X1、X2的样本取值范围之内,因而对截距项的解释要非常谨慎。
用EXCEL做线性回归的方法在Excel中进行线性回归分析是一种常见的统计方法，可以用来建立和评估两个变量之间的线性关系。
以下是在Excel中进行线性回归的步骤：2. 打开Excel并导入数据：在Excel中创建一个新的工作簿并将数据导入其中。
确保每个变量处于独立的列中，并将列标题放在第一行。
3.绘制散点图：选择包含两个变量的数据范围，然后通过选择“插入”选项卡上的“散点图”图标绘制散点图。
确保选择一个表示线性趋势的散点图类型（例如，线性散点图）。
4.添加趋势线：右键单击散点图上的任何一个数据点，然后选择“添加趋势线”选项。
在弹出的对话框中，选择“线性”作为趋势线类型。
还可以选择“显示方程式”和“显示R方值”，以显示方程式和决定系数。
5. 进行线性回归分析：在Excel中进行线性回归分析有两种常见的方法。
一种是使用“利用工具”功能进行线性回归，另一种是使用“数据分析”工具。
-利用工具：选择工作表中的一个空单元格，然后选择“数据”选项卡上的“数据分析”功能。
在弹出的对话框中，选择“回归”然后点击“确定”。
在输入区域中选择两个变量的列，并勾选“置信区间”和“残差”，然后点击“确定”进行分析。
- 数据分析工具：如果Excel中没有“数据分析”选项，则需要先启用。
选择“文件”选项卡上的“选项”，然后选择“添加-加载项”。
在弹出的对话框中，选择“Excel加载项”，并勾选“数据分析工具”，然后点击“确定”。
在“数据”选项卡上就会出现“数据分析”选项，然后执行和利用工具方法相同的步骤。
6. 解读结果：分析完成后，Excel将在单元格区域中输出回归方程式和其他相关统计信息。
主要关注回归方程式中的系数，这些系数表示参与线性回归的变量之间的关系。
还可以评估决定系数（R²）的值以确定回归模型的拟合程度。
7.绘制拟合曲线：使用回归方程式中的系数，可以在散点图中绘制拟合曲线。
选择散点图上的一个空白区域，然后选择“插入”选项卡上的“散点图”功能。
excel多元回归模型
Excel可以使用数据分析工具包中的回归分析功能进行多元回归分析。
使用该功能需要满足以下条件：
1. 数据符合多元线性回归的基本假设，即各自变量之间相互独立，且对应因变量的关系为线性关系。
2. 数据已输入Excel表格中，并按照自变量和因变量分列排列。
3. 安装并启用数据分析工具包。
下面是使用Excel进行多元回归的步骤：
步骤1：打开Excel表格，并打开“数据分析工具包”。
步骤2：选择“回归”功能，并点击“确定”。
步骤3：在“回归”对话框中填写以下信息：
i. 输入数据范围：选择自变量和因变量所在的单元格区域。
ii. 选择输出选项：选择需要计算的统计量，例如ANOVA表、系数、标准误差、t值等。
iii. 选择自变量：选择包含自变量的单元格区域。
iv. 选项：选择是否需要新增截距项，以及是否需要输出残差。
步骤4：点击“确定”按钮，Excel会自动对输入数据进行多元回归分析，并在新的工作表中显示回归结果的各项统计量。
需要注意的是，在进行多元回归分析之前，需要进行基本的数据清洗和预处理，例如删除缺失数据、处理异常值等。
此外，在解释回归结果时，还需注意各系数的显著性和实际意义。
使用Excel数据分析工具进行多元回归分析使用Excel数据分析工具进行多元回归分析与简单的回归估算分析方法基本相同。
但是由于有些电脑在安装办公软件时并未加载数据分析工具，所以从加载开始说起（以Excel2010版为例，其余版本都可以在相应界面找到）。
点击“文件”，如下图：在弹出的菜单中选择“选项”，如下图所示：在弹出的“选项”菜单中选择“加载项”，在“加载项”多行文本框中使用滚动条找到并选中“分析工具库”，然后点击最下方的“转到”，如下图所示：在弹出的“加载宏”菜单中选择“分析工具库”，然后点击“确定”，如下图所示：加载完毕，在“数据”工具栏中就出现“数据分析”工具库，如下图所示：给出原始数据，自变量的值在A2：I21单元格区间中，因变量的值在J2：J21中，如下图所示：假设回归估算表达式为：试使用Excel数据分析工具库中的回归分析工具对其回归系数进行估算并进行回归分析：点击“数据”工具栏中中的“数据分析”工具库，如下图所示：在弹出的“数据分析”-“分析工具”多行文本框中选择“回归”，然后点击“确定”，如下图所示：弹出“回归”对话框并作如下图的选择：上述选择的具体方法是：在“Y值输入区域”，点击右侧折叠按钮，选取函数Y数据所在单元格区域J2：J21，选完后再单击折叠按钮返回；这过程也可以直接在“Y值输入区域”文本框中输入J2：J21；在“X值输入区域”，点击右侧折叠按钮，选取自变量数据所在单元格区域A2：I21，选完后再单击折叠按钮返回；这过程也可以直接在“X值输入区域”文本框中输入A2：I21；置信度可选默认的95%。
在“输出区域”如选“新工作表”，就将统计分析结果输出到在新表内。
为了比较对照，我选本表内的空白区域，左上角起始单元格为K10.点击确定后，输出结果如下：第一张表是“回归统计表”(K12：L17):其中：Multiple R：（复相关系数R）R2的平方根，又称相关系数，用来衡量自变量x与y之间的相关程度的大小。
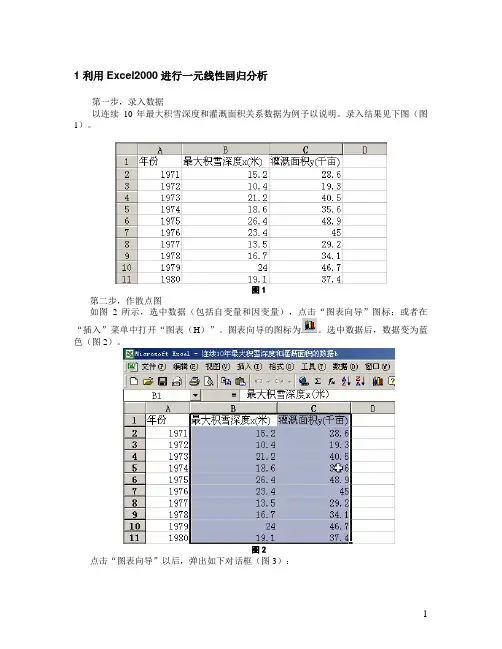
1 利用Excel2000进行一元线性回归分析第一步，录入数据以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。
录入结果见下图（图1）。
图1第二步，作散点图如图2所示，选中数据（包括自变量和因变量），点击“图表向导”图标；或者在“插入”菜单中打开“图表（H）”。
图表向导的图标为。
选中数据后，数据变为蓝色（图2）。
图2点击“图表向导”以后，弹出如下对话框（图3）：图3在左边一栏中选中“XY散点图”，点击“完成”按钮，立即出现散点图的原始形式（图4）：图4第三步，回归观察散点图，判断点列分布是否具有线性趋势。
只有当数据具有线性分布特征时，才能采用线性回归分析方法。
从图中可以看出，本例数据具有线性分布趋势，可以进行线性回归。
回归的步骤如下：⑴首先，打开“工具”下拉菜单，可见数据分析选项（见图5）：图5用鼠标双击“数据分析”选项，弹出“数据分析”对话框（图6）：图6⑵然后，选择“回归”，确定，弹出如下选项表（图7）：图7进行如下选择：X、Y值的输入区域（B1:B11，C1:C11），标志，置信度（95%），新工作表组，残差，线性拟合图（图8-1）。
或者：X、Y值的输入区域（B2:B11，C2:C11），置信度（95%），新工作表组，残差，线性拟合图（图8-2）。
注意：选中数据“标志”和不选“标志”，X、Y值的输入区域是不一样的：前者包括数据标志：最大积雪深度x(米)灌溉面积y(千亩)后者不包括。
这一点务请注意（图8）。
图8-1 包括数据“标志”图8-2 不包括数据“标志”⑶再后，确定，取得回归结果（图9）。
图9 线性回归结果⑷最后，读取回归结果如下：截距：356.2=a ；斜率：813.1=b ；相关系数：989.0=R ；测定系数：979.02=R ；F 值：945.371=F ；t 值：286.19=t ；标准离差（标准误差）：419.1=s ；回归平方和：854.748SSr =；剩余平方和：107.16SSe =；y 的误差平方和即总平方和：961.764SSt =。
利用Ｅxcel进行线性回归分析————————————————————————————————作者: ————————————————————————————————日期：ﻩ文档内容1.利用Excel进行一元线性回归分析２. 利用Ｅｘcｅｌ进行多元线性回归分析1．利用Excel进行一元线性回归分析第一步,录入数据以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。
录入结果见下图(图1)。
图1第二步,作散点图如图２所示，选中数据(包括自变量和因变量）,点击“图表向导”图标；或者在“插入”菜单中打开“图表(H)”。
图表向导的图标为。
选中数据后，数据变为蓝色(图２）。
图2点击“图表向导”以后，弹出如下对话框(图３）:图3在左边一栏中选中“XＹ散点图”，点击“完成”按钮,立即出现散点图的原始形式（图4)：灌溉面积y(千亩)01020304050600102030灌溉面积y(千亩)图４第三步，回归观察散点图,判断点列分布是否具有线性趋势。
只有当数据具有线性分布特征时,才能采用线性回归分析方法。
从图中可以看出，本例数据具有线性分布趋势，可以进行线性回归。
回归的步骤如下:1. 首先，打开“工具”下拉菜单，可见数据分析选项（见图5）：图５用鼠标双击“数据分析”选项,弹出“数据分析”对话框（图6)：图62.然后，选择“回归”，确定，弹出如下选项表(图7)：图7进行如下选择：X 、Y 值的输入区域(B1：Ｂ11，C1:C11）,标志,置信度(95%),新工作表组，残差,线性拟合图(图８-１）。
或者:X 、Y 值的输入区域（B2:B11，C2:Ｃ11)，置信度(95%)，新工作表组,残差,线性拟合图（图8-2）。
注意：选中数据“标志”和不选“标志”,X 、Y 值的输入区域是不一样的：前者包括数据标志：最大积雪深度x （米) 灌溉面积y （千亩）后者不包括。
这一点务请注意(图8）。
图８－1包括数据“标志”图8-２不包括数据“标志”3.再后，确定,取得回归结果(图9）。
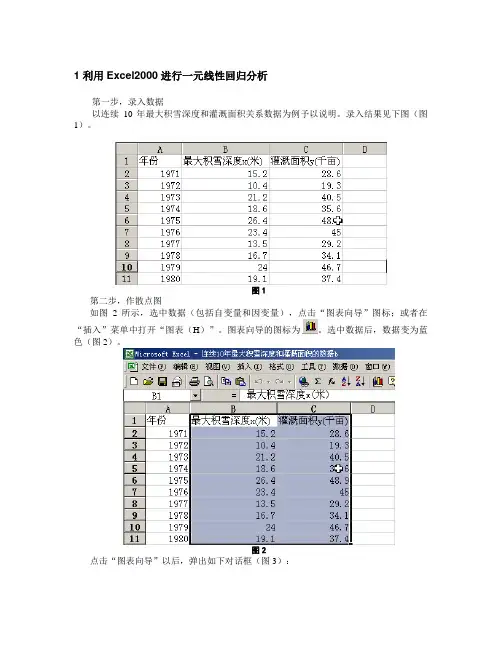
1 利用Excel2000进行一元线性回归分析第一步，录入数据以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。
录入结果见下图（图1）。
图1第二步，作散点图如图2所示，选中数据（包括自变量和因变量），点击“图表向导”图标；或者在“插入”菜单中打开“图表（H）”。
图表向导的图标为。
选中数据后，数据变为蓝色（图2）。
图2点击“图表向导”以后，弹出如下对话框（图3）：图3在左边一栏中选中“XY散点图”，点击“完成”按钮，立即出现散点图的原始形式（图4第三步，回归观察散点图，判断点列分布是否具有线性趋势。
只有当数据具有线性分布特征时，才能采用线性回归分析方法。
从图中可以看出，本例数据具有线性分布趋势，可以进行线性回归。
回归的步骤如下：⑴首先，打开“工具”下拉菜单，可见数据分析选项（见图5）：图5用鼠标双击“数据分析”选项，弹出“数据分析”对话框（图6）：图6⑵然后，选择“回归”，确定，弹出如下选项表：图7进行如下选择：X、Y值的输入区域（B1:B11，C1:C11），标志，置信度（95%），新工作表组，残差，线性拟合图。
或者：X、Y值的输入区域（B2:B11，C2:C11），置信度（95%），新工作表组，残差，线性拟合图。
注意：选中数据“标志”和不选“标志”，X、Y值的输入区域是不一样的：前者包括数据标志：最大积雪深度x(米)灌溉面积y(千亩)后者不包括。
这一点务请注意。
图8-1 包括数据“标志”图8-2 不包括数据“标志”⑶再后，确定，取得回归结果（图9）。
图9 线性回归结果⑷最后，读取回归结果如下：截距：356.2=a ；斜率：813.1=b ；相关系数：989.0=R ；测定系数：979.02=R ；F 值：945.371=F 。
⑸ 建立回归模型，并对结果进行检验模型为：x y813.1356.2ˆ+= 至于检验，R 、R 2和F 值可以直接从回归结果中读出。
实际上，8,05.0632.0989416.0R R =>=，检验通过。
[精品WORD]教你用Excel做回归分析用Excel进行回归分析可以很方便地对数据进行分析和预测。
以下是使用Excel进行回归分析的步骤和解释：1.导入数据首先，将需要分析的数据导入Excel中。
可以在Excel的菜单栏中选择“数据”，然后选择“导入外部数据”或“从数据库导入数据”。
导入数据后，将数据放置在一个表格中。
2.选中数据在Excel表格中选中包含数据的区域。
确保包含需要分析的数据，以及任何其他相关的数据列。
3.插入图表在Excel的菜单栏中选择“插入”，然后选择“图表”。
在图表类型中选择适合的数据类型，例如线性图、散点图等。
在弹出的对话框中，选择需要分析的数据区域，并设置图表的其他选项。
4.添加趋势线在图表中单击鼠标右键，选择“添加趋势线”。
在弹出的对话框中，选择要添加趋势线的图表类型，例如线性、指数、对数等。
选择要添加趋势线的数据系列，并设置趋势线的其他选项。
5.显示回归分析结果在趋势线对话框中，选择“显示公式”和“显示R平方值”。
这将显示回归分析的结果，包括回归线的公式和R平方值。
R平方值越接近1，说明回归模型越精确。
6.分析回归结果根据回归分析的结果，可以得出以下结论：•斜率：回归线的斜率表示自变量对因变量的影响程度。
斜率越大，影响程度越大。
•截距：回归线的截距表示因变量在自变量为0时的值。
•R平方值：R平方值表示回归模型对数据的拟合程度。
如果R平方值接近1，说明模型拟合度较高。
•F值：F值是进行回归分析时的统计量，表示整个回归模型的显著性。
如果F值较大，说明模型显著性较高。
•P值：P值表示自变量对因变量的影响是否显著。
如果P值小于0.05，说明自变量对因变量的影响是显著的。
7.使用回归模型进行预测根据回归分析的结果，可以使用回归模型对未来数据进行预测。
将自变量的预测值代入回归模型中，即可得出因变量的预测值。
总之，使用Excel进行回归分析可以方便地得出数据的回归分析结果，以及对未来数据进行预测。
用EXCEL进行生产函数的多元线性回归分析一、相关函数EXCEL电子制表系统中函数的语法分为函数名和参数两部分，参数用圆括号括起来，之间以逗号隔开。
参数可以为单元格区域、数组、函数、常数（逻辑型、数值型等）。
进行回归分析时，主要采用线性回归函数LINEST，辅以使用索引取值INDEX与四舍五入ROUND 函数。
1、线性回归函数LINEST。
使用最小二乘法对已知数据进行最佳直线拟合，并返回描述此直线的数组。
因为此函数返回数值数组，所以必须以数组公式的形式输入。
Excel中数组公式非常有用，它可建立产生多值或对一组值而不是单个值进行操作的公式。
要输入数组公式，首先必须选择用来存放结果的单元格区域，在编辑栏输入公式，然后按ctrl＋Shift＋Enter 组合键锁定数组公式，Excel将在公式两边自动加上括号“{}”。
不要自己键入花括号，否则，Excel认为输入的是一个正文标签。
要编辑或清除数组公式．需选择数组区域并且激活编辑栏，公式两边的括号将消失，然后编辑或清除公式，最后按Ctrl＋shift＋Enter键。
【实现目标】在Excel中巧编辑数组公式。
【操作方法】其具体操作如下：（1）选择用来存放结果的单元格区域，在编辑栏输入公式，然后按【Ctrl＋Shift＋Enter】键锁定数组公式，Excel将在公式两边自动加上括号“{}”。
（2）编辑或清除数组公式时，先选择数组区域并且激活编辑栏，然后编辑或清除公式，最后按【Ctrl＋Shift＋Enter】键即可。
该函数的功能为：运算结果返回一线性回归方程的参数，即当已知一组混合成本为Y因变量序列值、N组Xi有关自变量因素的数量序列值时，函数返回回归方程的系数bi（i=1，2…n单位变动成本）和常数a（固定成本或费用）。
多元回归方程模型则为：y=b1x1＋b2X2……＋bnXn＋a语法LINEST(known_y's,known_x's,const,stats)Known_y's 是关系表达式 y = mx + b 中已知的 y 值集合。
