大学物理2期末复习要点
- 格式:doc
- 大小:181.50 KB
- 文档页数:4

各章重点§8库仑定律F 12=k q 1q 2r 123r 12 k=9.0*109N.m 2/C 2ε0=8.85×10−12C 2/(N ∙m 2)真空中库仑定律F 21=−F 12=14πεq 1q 2r 213r 21电场强度E =Fq 0F =14πεqq 0r 3rE =q4πε0r 3rE = qi4πε0r i3r i n i =1§9静电场中的电介质D =E0ε真空中E rεε0介质中高斯定理⎰∑=∙Si q S d D电容电容器孤立导体uqC=电容器BA u u qC -=电场能量电容器Qu Cu C Q W 2121222===电场⎰=VwdV W 电场能量密度:221E w ε=求C 的方法定义法AB AB U C U E q q =→→→能量法W qC W w E q 22=→→→→§10&11 电流强度、电流密度dt dq I =n dS dI j⊥=l d E l d E kl k⋅=⋅=⎰⎰内ε(E K 为非静电场强)磁通量⎰⋅=Φs m S d B 磁场的计算34r rl Id B d⨯=πμ⎰⨯=34r r l Id Bπμ⎰=B d B∑⎰=⋅il I l d B0μ304rr q B⨯=υπμ磁场方程⎰=⋅S S d B 0 ⎰∑=⋅l i I l d B 0μ 载流线圈的磁矩n NIS P m=电磁相互作用B l Id f d ⨯=⎰⨯=lB l Id f B P M m ⨯=B q F⨯=υ⎰ΦΦΦ=21m m m Id A 霍耳电压b IB R U H H =霍耳系数)1(nqR H =直电流的磁场)cos (cos 4210ααπμ-=a I B 无限长载流直导线aIB πμ20=半无限长载流直导线a I B πμ40=直导线延长线上0=B 2. 圆电流轴线上某点的磁场大小232220)(2x R IR B +=μ右手螺旋法则载流圆环圆心处的B 圆心角R I B 20μ=载流圆弧圆心角R I R I B πθμπθμ42200=∙=长直载流螺线管⎩⎨⎧=外0内0nI B μ无限大载流导体薄板0nI B μ=环形载流螺线管⎪⎩⎪⎨⎧=外内20rNIB πμ2121、R R R R ->>12R Nn π=nI B 0μ≈ §13自感系数IL mψ=自感电动势dt dI Ll -=ε互感系数12121I M ψ=21212I M ψ=M M M ==1221互感电动势dt dI M 121-=εdtdI M 212-=ε动生电动势⎰⋅⨯=l d B v iε电磁感应定律dtd mi Φ-=ε 感生电动势S d tBl d Es l i⋅∂∂-=⋅=⎰⎰涡ε课本例题电流的功率PPT 例题※在截面半径为R 的圆柱形空间充满磁感应强度为B 的均匀磁场, B 的方向沿圆柱形轴线 , B 的大小随时间按dB /dt = k 的规律均匀增加 , 有一长L =2R 的金属棒abc 位于图示位置,求金属棒中的感生电动势.解: 作辅助线oa 、oc 构== 成闭合回路oabco 。



大学物理2复习总结一、知识点回顾大学物理2是物理学的一个重要分支,它涵盖了力学、电磁学、光学、热学等多个方面的知识。
在复习过程中,我首先对各个知识点进行了回顾,包括:牛顿运动定律、动量守恒定律、能量守恒定律、电场强度、电势、磁场、光的干涉和衍射、波动等。
通过对这些知识点的复习,我巩固了基础,为后续的解题打下了坚实的基础。
二、重点难点解析在复习过程中,我发现有一些知识点是特别重要的,也是我在学习中遇到的难点。
比如,牛顿运动定律的综合应用、电磁场的理解、光的干涉和衍射的原理和计算等。
对于这些重点难点,我进行了深入的分析和理解,通过大量的例题和练习题来加深对这些知识点的理解和掌握。
三、解题方法总结大学物理2的解题方法非常重要,掌握了解题方法,才能更好地解决各种问题。
在复习过程中,我总结了一些常用的解题方法,如:牛顿运动定律的矢量表示、动量守恒定律的代数表示、能量守恒定律的综合应用、电场强度的计算、电势的计算、磁场的计算、光的干涉和衍射的计算等。
通过这些方法的掌握,我能够更好地解决各种问题。
四、错题总结与反思在复习过程中,我发现自己在一些问题上容易出错,比如:对牛顿运动定律的理解不够深入、对电磁场的理解不够准确、对光的干涉和衍射的计算不够熟练等。
对于这些问题,我进行了总结和反思,分析了出错的原因,并通过大量的练习来避免类似的错误再次发生。
五、知识框架构建在复习结束后,我构建了大学物理2的知识框架,将各个知识点有机地在一起。
通过这个知识框架,我能够更好地理解和掌握大学物理2的知识点,也能够更好地应用这些知识点解决实际问题。
六、备考策略优化在备考过程中,我还优化了自己的备考策略。
我制定了详细的复习计划,将每个知识点都安排在合理的复习时间内。
我注重了课堂听讲和笔记整理的结合,确保自己对每个知识点都有深入的理解。
我注重了练习和反思的结合,通过大量的练习来提高自己的解题能力,同时不断反思自己的解题方法和思路。
通过这次复习总结,我对大学物理2有了更深入的理解和掌握,同时也提高了自己的解题能力和思维能力。

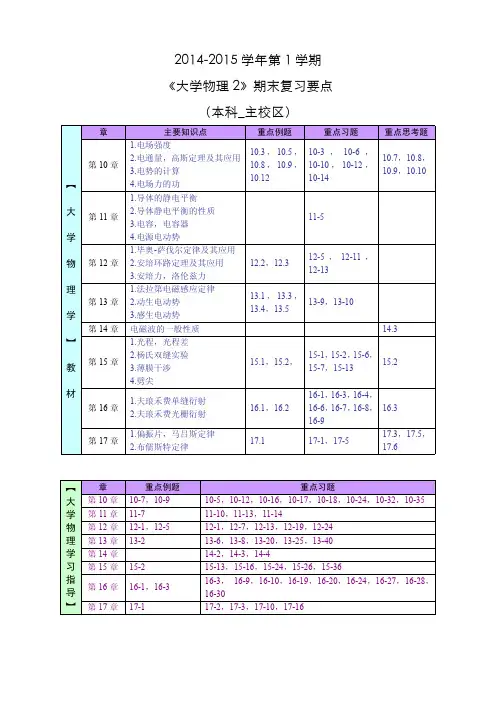


《大学物理(二)》 期末考试要点汇总热力学1.掌握内能、功和热量等概念,理解平衡态、准静态过程等概念。
2.掌握热力学第一定律,能分析、计算理想气体在等体、等压、等温和绝热过程中的功、热量、内能的改变量.3.理解循环的意义和循环过程中的能量转换关系,会计算卡诺循环和其他简单循环的效率.4.掌握热力学第二定律的两种表述及实质.气体动理论1.能均分定理,温度的统计意义,速率分布函数的物理意义2.根据速率分布函数解释物理意义,方均根速率,能均分定理(平均动能)3.理想气体的压强公式、状态方程,能均分定理(平动动能,转动动能)4.热运动与宏观运动的区别机械振动基础1. 掌握常见的谐振动模型,如弹簧振子的小幅度,单摆、复摆的小角度振动都是谐振动,并会运用简谐运动规律对其讨论和分析。
尤其重点掌握弹簧振子的小幅度振动,即弹簧振子的谐振动中先行回复力中各量的内在含义。
2. 掌握描述简谐运动的各个物理量(特别是相位)的物理意义及各量间的关系。
3. 掌握简谐运动的基本特征,能建立一维简谐运动的微分方程,能根据给定的初始条件写出一维简谐运动的运动方程,并理解其物理意义,能写出速度和加速度随时间变化的函数,会运用函数讨论和分析问题。
4. 掌握谐振动的能量(动能、势能以及机械能)的物理意义,会运用能量的公式进行讨论和分析。
5. 掌握描述简谐运动的旋转矢量法,并会用于简谐运动规律的讨论和分析。
6. 理解同方向、同频率简谐运动的合成规律,会运用合成规律进行讨论和分析。
机械波1. 了解机械波中横波和纵波的定义,了解波面和波线以及波前的定义。
2. 掌握相位、波长、周期、频率和波速的定义,并且理解在简谐振动和简谐波中这些物理量之间的关系。
3. 掌握平面简谐波的波函数表达式中各个物理量的含义,根据已知条件能够写出左行波和右行波的波函数,会运用质元的位移、速度函数。
4. 掌握质元的振动方程图和任意时刻的波形图的画法。
会解释任一质元处的波函数的意义。

《大学物理2》期末复习参考第九章静电场1、 场强叠加原理(离散带电体系玄艮、连续带电体系2、 局斯定理0e = ^£• d5 = —^q, os ^0 1=1 (1) 什么是高斯面?高斯定理证明了静电场的什么特性?(2) 穿过高斯面的电通量与高斯面内、外的电荷有什么关系?(3) 高斯定理中的£与高斯面内、外的电荷有什么关系?(4) 如何用高斯定理求具有对称性的带电体的场强分布?(5) 可以利用高斯定理求电偶极子的场强分布吗?3、 静电场力做功。
(1)静电场力做功有什么特点?(2)静电场的环路定理f z ^df = 0证明了静电场的什么特性?电场弱的地方电势低;电场强的地方电势高吗?这个瞰不对。
m 场反映的P^r4权0 AV )r=o 点 4、 电势匕=\E AI :电势差:'AB £ dZ o 5、 电势叠加原理:匕4 7T£o f 6、 电势梯度:AV ~dT其中的负号代表什么意思?场强相等的地方,电势也一定相等吗?在静暢中,个她势-记相等,场强大小不一定相等(1)等势面有什么特点?在等势面移动一个正电荷做正功还是负功?不做功第十章静电场中的导体和电介质什么是静电场平衡条件?导体处于静电平衡时有什么特点?处r静电平衡的导体,其静电荷只能分布在导体的外表而,导体内电场强处处为零,导体是一个等势体,导体表而的场强方向垂直于导体表面1、静电平衡导体上的电荷如何分布?只分布在表面2、静电场中的电介质有那两种?无极分子和有级分子当电场中充入了电介质以后,总电场是增强还是减弱?减小相对电容率(£ =—)的物理意义是什么?:物质的绝对屯容率与也常数之比3、如何计算球形电容器、柱形电容器、平板电容器的电容?电容器中充入电介质以后电容将增大还是减小?增大电容器中的能量储存在什么地方?电场中第十一章恒定磁场电流密度与电流强度有什么关系?电流强度越大,电流密度也越大1、为什么要引入电流密度的概念?导线屮不冋点上与电流A向里•直的吶位面积.1:流过什么是电源的电动势(E = ^E k dl=^E k dl ) ?非静电力是保守 力吗? 非静电力是非保守力。


大二物理知识点总结一、力学力学是物理学的一个重要分支,研究物体的运动规律和相互作用关系。
大二力学主要包括以下知识点:1. 运动学运动学研究物体的运动状态和运动规律,主要包括位移、速度、加速度等概念。
重要知识点包括:(1)位移:物体在运动过程中位置的变化量。
(2)速度:物体单位时间内所经过的路程。
(3)加速度:速度的变化率,即单位时间内速度的变化量。
(4)匀速直线运动和变速直线运动:物体在运动过程中速度是否恒定的情况。
2. 动力学动力学研究物体受力作用时的运动规律,主要包括牛顿三定律、动量定理、动能定理等概念。
重要知识点包括:(1)牛顿三定律:第一定律(惯性定律)、第二定律(运动定律)、第三定律(作用—反作用定律)。
(2)动量定理:物体受力作用时,动量的变化率等于所受合外力。
(3)动能定理:物体的动能变化等于所受合外力做功。
(4)万有引力定律:两个物体之间的引力与它们的质量和距离的平方成正比。
3. 转动力学转动力学研究物体绕轴的旋转运动规律,主要包括角度、角速度、角加速度等概念。
重要知识点包括:(1)角度:物体在圆周上所对的角。
(2)角速度:物体单位时间内绕轴旋转的角度。
(3)角加速度:角速度的变化率,即单位时间内角速度的变化量。
(4)转动惯量:物体对围绕着的轴的转动难易程度。
(5)角动量:物体绕轴旋转时的动量大小。
二、电磁学电磁学是研究电荷的相互作用和电磁场的性质的学科。
大二电磁学主要包括以下知识点:1. 静电学静电学研究带电物体之间的相互作用和电场的性质,主要包括库仑定律、电场强度、电势等概念。
重要知识点包括:(1)库仑定律:两个带电物体之间的电力与它们之间的距离的平方成反比、与它们的电量乘积成正比。
(2)电场强度:在某一点的电场力与单位正电荷所受到的力。
(3)电势:单位正电荷在电场中具有的电势能。
2. 电动力学电动力学研究带电粒子在电场和磁场中的运动规律,主要包括洛伦兹力、磁感应强度、磁场能量等概念。
大学物理(二)总复习第九章振动一、基本概念1、简谐振动的三种定义方式(判据):(1)振动物体在弹性回复力的作用下,只要满足= 这一关系,就称作简谐振动。
X(2)振动物体满足微分方程:--afx = O,就称作简谐振动。
(3)—个物体的运动方程是:x=4cos(血+ 0)的形式,就称之为简谐振动。
2、简谐振动的运动方程为:x=Acos(69f + 0)要深刻理解方程中各项的物理意义,简谐振动的三要素:A 秋门、(血+0),3、单摆和复摆(在其摆角很小的情况卞,其摆动是角谐振动,周期分别为:4、简谐振动系统的总机械能E是守恒的,在振动的一个周期内,平均动能和平均势能是相等的,即-— 1E+E=E5、简谐振动的合成重点掌握两个同方向同频率的简谐振动的合成规律。
二、典型例题1、如题4-3图所示,物体的质量为加,放在光滑斜面上,斜面与水平面的夹角为&,弹簧的倔强系数为比,滑轮的转动惯量为/,半径为/?.先把物体托住,使弹赞维持原长,然后由静止释放,试证明物体作简谐振动,并求振动周期.(a)mg解:分别以物体加和滑轮为对象,其受力如题4-3图(b)所示,以重物在斜面上静平衡时位 置为处标原点,沿斜面向下为兀轴正向,则当重物偏离原点的处标为兀时,有T,R-T 2R = Ip式中X()=mgsin0/k f 为静平衡时弹簧Z 伸长量,联立以上三式,有kR1mR 2 +1则有d 2xdr 7故知该系统是作简谐振动,其振动周期为2、 一轻弹簧的倔强系数为k,其下端悬有--质量为M 的盘子.现有一质量为加的物体 从离盘底力高度处自山下落到盘中并和盘子粘在一•起,于是盘子开始振动. ⑴此时的振动周期与空盘了作振动时的周期冇何不同? ⑵此时的振动振幅多大?(3)取平衡位宜为原点,位移以向下为正,并以弹簧开始振动时作为计时起点,求初位相并 写出物体与盘子的振动方程.MM + m解:(1)空盘的振动周期为2龙」牙,落下重物后振动周期为即增大.mg sin 0 - £ =d 2xdi 7= R/3 T 2 = P (兀 o + x )⑵按⑶所设处标原点及计时起点,r = ont,则x ()=-^-.碰撞时,以加,M 为一系统 k 动量守恒,即m』2gh = (77? + M )t>0则冇于是(3)叫宀爲(第三象限)’所以振动方動第十章波动一、基本概念1、 机械波的形成(产生机械波的条件)2、 波的波长、周期和频率,波速3、 波线、波而、波前(波阵而)4、 平而简谐波的波函数y = A cos Q(/——) u重点掌握波函数的物理意义。
1 位移电流的实质是什么?谈谈你对位移电流的理解。
答:位移电流的本质是变化的电场。
d ==t t D d dD I S d d ψ 位移电流密度d d 1j ==dt t D dD S d ψ 位移电流是电位移通量对时间的变化率。
位移电流只对应于变化的电场,无自由电荷的定向移动,无焦耳热。
在导体、电介质、真空中均存在,只要有变化的电场就有位移电流。
2 行波在传播过程中,质元的动能和势能的时间关系式是相同的。
就此谈谈你的理解? 答:在介质中任取体积为△V ,质量为△m 的质元。
当波传播到这个质元时,将具有动能△Ek 和△Ep 。
可以证明 222p 01==()sin 2K x E E A V t u ρωωϕ⎡⎤⎛⎫∆-+ ⎪⎢⎥⎝⎭⎣⎦△△在波传播的媒质中,任一体积元的动能和势能还有总机械能均随x ,t 作周期性变化,且变化是同相位的。
体积元在平衡位置时,动能势能和机械能均最大。
体积远的位移最大时,三者均为零。
3 什么是波的衍射?举出生活中关于波的衍射的例子。
什么是波的干涉?相干光的获得方法有哪些?答:衍射:当波在传播过程中遇到障碍物时,其传播方向绕过障碍物发生偏折的现象,称为波的衍射。
例如站在高墙后面的人能听到别人说话的声音,隔了山岭或者建筑物能收听无线电广播。
干涉:频率相同的两列波叠加,使某些区域的振动加强,某些区域的振动减弱,而且振动加强的区域和振动减弱的区域相互隔开。
这种现象叫做波的干涉。
产生干涉的一个必要条件是,两列波的频率必须相同并且有固定的相位差。
获得相干光的方法的基本原理是把由光源上同一点发出的光设法一分为二,然后再使这两部分叠加起来。
1分波阵面法(例如杨氏双缝干涉) 2分振幅法(例如薄膜干涉)。
4 杨氏双缝实验中,屏上的干涉条纹有怎样的特点,明暗条纹的级次和间距由哪些因素决定?答:屏上将出现一系列稳定的明暗相间的条纹。
这些条纹都与狭缝平行,条纹间的距离彼此相等。
如果,P 点处为明纹,即各级明纹中心离O 点的距离为x=k d D λ± k=0,1,2,3,……相应于k=0的称为零级明纹或中央明纹。
大学物理II 期末复习1、图示为一个均匀带电的球层,其电荷体密度为ρ,球层内表面半径为1R ,外表面半径为2R .设无穷远处为电势零点,求空腔内任一点的电势.解法1: 由高斯定理可知空腔内E =0,故带电球层的空腔是等势区,各点电势均 为U . 在球层内取半径为r r dr →+的薄球层.其电荷为24dq r dr ρπ=该薄层电荷在球心处产生的电势为()00/d 4/d d ερεr r r q U =π= 整个带电球层在球心处产生的电势为()21220002d d 21R R r r U U R R -===⎰⎰ερερ 因为空腔内为等势区所以空腔内任一点的电势U 为()2122002R R U U -==ερ 解法2:由高斯定理可知1r R <,10E =, 2分12R r R <<,331220()r R E r ρε-=, 2r R >,3321320()R R E rρε-= 若根据电势定义⎰⋅=l E Ud空腔内任一点电势为:12121230R R R R U E dr E dr E dr ∞=++⎰⎰⎰()222102R R ρε=- 2、如图所示,两个共面的平面带电圆环,其内外半径分别为1R 、2R 和2R 、3R ,外面的圆环以每秒钟2n 转的转速顺时针转动,里面的圆环以每秒钟1n 转的转速反时针转动.若电荷面密度都是σ,求1n 和2n 的比值多大时,圆心处的磁感强度为零.解:(1) 在内圆环上取半径为r 宽度为dr 的细圆环,其电荷为σr r q d 2d π= 由于转动而形成的电流 r rn q n i d 2d d 11σπ==di 在O 点产生的磁感强度为r n r i B d )2/(d d 1001σμμπ==其方向垂直纸面向外.(2) 整个内圆环在O 点产生的磁感强度为==⎰11d B B ⎰π21d 10R R r n σμ)(121R R n -π=0σμ其方向垂直纸面向外.(3) 同理得外圆环在O 点产生的磁感强度)(23203R R n B -π=σμ 其方向垂直纸面向里. (4) 为使O 点的磁感应强度为零,B 1和B 2的量值必须相等, 即 )(121R R n -π0σμ)(232R R n -π=0σμ于是求得n 1和n 2之比122312R R R R n n --=3、一电子以0.99v c =(c 为真空中光速)的速率运动.试求: (1) 电子的总能量是多少焦耳?(2) 电子的相对论动能是多少焦耳?(电子静止质量319.1110kg e m -=⨯)解:(1) 222)/(1/c c m mc E e v -===5.8×10-13 J(2) 22k e E mc m c =-= 4.99×10-13 J4、两根平行无限长直导线相距为d ,载有大小相等方向相反的电流I ,电流变化率0dI dt a =>.一个边长为d 的正方形线圈位于导线平面内与一根导线相距d ,如图所示.求线圈中的感应电动势ε,并指出线圈中的感应电流是顺时针还是逆时针方向.解:(1) 载流为I 的无限长直导线在与其相距为r 处产生的磁感强度为:)2/(0r I B π=μ以顺时针绕向为线圈回路的正方向,与线圈相距较远的导线在线圈中产生的磁通量为:300123d ln222ddIIdd r rμμφ=⋅=⎰ππ与线圈相距较近的导线对线圈的磁通量为:2002d ln 222ddIIdd r r μμφ=-⋅=-ππ⎰总磁通量 0124ln 23Id μφφφ=+=-π 2分感应电动势为: 00d 4d 4(ln )ln d 23d 23d d I a t t μμφε=-==ππ (2) 线圈中的感应电流是顺时针方向.5、用波长00.1nm λ=的光子做康普顿散射实验.(1) 散射角o 90ϕ=的康普顿散射波长是多少? (2) 反冲电子获得的动能是多少焦耳? (普朗克常量346.6310h -=⨯J ·s ,电子静止质量319.1110kg e m -=⨯)解:(1) 康普顿散射光子波长改变: ()(1cos )e hm cλϕ∆=-=0.024×10-10 m =+=∆λλλ0 1.024×10-10 m(2)根据能量守恒: 220e h m c h mc νν+=+即 220k e E mc m c h h νν=-=-0//k E hc hc λλ=-故k E =4.66×10-17 J =291 eV6、电荷Q (Q >0)均匀分布在长为L 的细棒上,在细棒的延长线上距细棒中心O 距离为a 的P 点处放一电荷为q (q >0 )的点电荷,求带电细棒对该点电荷的静电力.解:沿棒方向取坐标Ox ,原点O 在棒中心处.求P 点场强:()()20204d 4d d x a xx a q E -π=-π=ελε ()⎰--π=2/2/204d L L x a xE ελ()2202/2/0414L a Qx a L L -π=-⋅π=-εελ 方向沿x 轴正向. 点电荷受力:==qE F ()2204πL a qQ-ε方向沿x 轴正方向.7、图所示为两条穿过y 轴且垂直于x -y 平面的平行长直导线的正视图,两条导线皆通有电流I ,但方向相反,它们到x 轴的距离皆为a .(1) 推导出x 轴上P 点处的磁感强度)(x B 的表达式.(2) 求P 点在x 轴上何处时,该点的B 取得最大值.解:(1) 利用安培环路定理可求得1导线在P 点产生的磁感强度的大小为:r I B π=201μ2/1220)(12x a I +⋅π=μ 2导线在P 点产生的磁感强度的大小为: r I B π=202μ2/1220)(12x a I +⋅π=μ 1B 、2B 的方向如图所示. P 点总场 θθcos cos 2121B B B B B x x x +=+= 021=+=y y y B B B )()(220x a Iax B +π=μ,i x a Iax B)()(220+π=μ(2) 当 0d )(d =x x B ,0d )(d 22=<xx B 时,B (x )最大. 由此可得:x = 0处,B 有最大值.8、如图所示,一电荷线密度为λ的长直带电线(与一正方形线圈共面并与其一对边平行)以变速率v =v (t )沿着其长度方向运动,正方形线圈中的总电阻为R ,求t 时刻方形线圈中感应电流i (t )的大小(不计线圈自身的自感).解:长直带电线运动相当于电流λ⋅=)(t I v . 正方形线圈内的磁通量可如下求出d d 2Ia x a x μφ=⋅π+000d ln 222ax Ia Ia a x μμφ==⋅π+π⎰0d d ln 2d 2d i a It tμφε=-=π2ln d )(d 20t t a v λμπ=d ()()ln 22d it i t aRRtεμλ==πv9、一艘宇宙飞船的船身固有长度为L 0 =90 m ,相对于地面以=v 0.8 c (c 为真空中光速)的匀速度在地面观测站的上空飞过.(1) 观测站测得飞船的船身通过观测站的时间间隔是多少?(2) 宇航员测得船身通过观测站的时间间隔是多少?解:(1) 观测站测得飞船船身的长度为=-=20)/(1c L L v 54 m则 ∆t 1 = L /v =2.25×10-7 s(2) 宇航员测得飞船船身的长度为L 0,则∆t 2 = L 0/v =3.75×10-7s10、已知粒子在无限深势阱中运动,其波函数为)/sin(/2)(a x a x π=ψ (0 ≤x ≤a )求发现粒子的概率为最大的位置.解:先求粒子的位置概率密度)/(sin )/2()(22a x a x π=ψ)]/2cos(1)[2/2(a x a π-=当 1)/2c o s(-=πa x 时, 2)(x ψ有最大值.在0≤x ≤a 范围内可得 π=πa x /2 ∴ a x 21=.a。
2011年应院大学物理(2)期末复习要点一条条过关,要求理解掌握能会的内容重点过关,做到活学活用概念规律是基础必须默写,重要习题会做。
*1.理解电场强度和电势的叠加原理,会计算带电直线和带电圆弧细线的产生的电场强度和电势。
依据电荷分布求场强0204r rdq E Q ⎰=πε ,依据电荷分布求电势⎰=r dq 04πεϕ。
*2.理解静电场的高斯定理,会根据电荷的对称性分布计算某点的电场强度分布和电势分布。
会求均匀带电球体产生的电场强度分布,会求均匀带电圆柱面(体)产生的电场强度分布;会求均匀带电平面产生的电场强度分布,重要的是组合情况会求。
3. 会用电场强度与电势的积分关系计算某点的电势(先求电场强度分布)。
会计算电场能量密度和静电场能量。
两点电势差 ⎰∙=-2·112路径r d Eϕϕ,电势能改变)(12ϕϕ-=q W ,电场能密度212m E ωε=,电场力F qE =. 4.静电平衡导体的性质及应用,电介质中的高斯定理的含义,电容定义与计算,电容器储存的电能 22122e Q W CU C==的计算,D 与E 的关系D E ε=。
5.磁力、磁矩、磁力矩的计算 B v q f ⨯=,⎰⨯=)(B l Id F ,dI e S m n ⎰= , B m M ⨯=,ϕsin ISB M =,会求电荷圆周运动磁矩和载流平面线圈在磁场中转动磁力矩变化和功。
*6毕奥-萨伐尔定律及其计算结果的应用 会求组合通电细线电流磁场。
直线段电流磁场 )c o s (c o s 4210θθπμ-=a I B ,圆弧电流在圆心的磁场 RI B πθμ40=. *7安培环路定律及其应用,会求无限长通电圆柱体内外的磁场分布,求长直螺线管的磁场。
会利用磁场叠加原理分析计算B. 会求磁通量⎰∙=S d B m φ8.磁介质的分类,B 与H 的关系H B μ=及其应用,三种磁介质的磁化曲线比较。
*9.掌握动生电动势⎰∙⨯=l d B v )(ε和感生电动势的计算方法,自感系数和互感系数的计算I L mφ= ,1221M M =,自感磁能221LI W m =,磁能密度221122m H B ωμμ==。
*10.位移电流的产生原因与计算,默写麦克斯韦方程组及物理意义,默写电磁波的性质。
比较静电场规律与稳恒电流磁场规律。
位移电流与传导电流有何异同。
感生电场和静电场有何异同。
*11.黑体辐射 光电效应方程及应用,测不准关系及应用,物质波,波函数的意义与条件,薛定谔方程,描述原子状态的四个量子数特征,以上量子力学思想各是哪个科学家提出的。
比较机械波、电磁波与物质波的异同。
12.计算电场强度和电势各有哪些方法,测量温度有哪些方法。
13.重要习题:教材上习题12.4,12.13,12.21,13.4,13.12,13.13,13.14,14.1,14.3,14.6,14.11,14.12,14.15,16.2,16.10,16.16,17.4,17.5,17.11,17.13,17.20,17.21填空题1. 两个点电荷Q 1,Q 2相距为r ,电势能为-----------。
2. 一点电荷Q 位于正方体的中心,则其一个侧面的电通量为----------,若点电荷Q 位于半球面的球心,则半球面上电通量为--------。
3. 半径为R 的均匀带电球体,电荷体密度为ρ,则离球心为R/2处的一点电场强度--------,离球心距离为3R 处一点的电场强度是----------。
电场能密度最大处r=----------。
4. 半径为R 的均匀带电球体,电荷体密度为ρ,则离球心为R/2处的一点电势是--------,离球心距离为3R 处一点的电势是----------。
5. 两个无限大均匀带电平板,电荷面密度分别为3σσ和,平行放置,则两板间的电场强度大小是---------,两板外侧电场强度大小是----------。
6. 半径为R 电量为Q 的均匀带电球壳球心处的电势是----------,离球心距离为2R 一点的电势是---------。
球壳内一点电场能量密度是------------。
7. 静电场的环路定理是-------------------------------------------。
它表明静电场是------场。
静电场的高斯定理是--------------,表明静电场是------场。
若闭合曲面上的D 通量为零,则闭合曲面内自由电荷--------。
(代数和为零)8. 导体处于静电平衡时,导体表面附近电场强度为E ,则电场强度方向与表面-------,该处附近导体表面的电荷密度是--------。
9. 平行板电容器带电为Q ,极板间无电介质时电容为C 0,电场强度为E 0,将相对介电常数为r ε的电介质插入电容器极板间后,极板间电场强度是-------,电位移矢量D=---------,两极板的电势差是-----------,电容是--------,外力克服电场力做功是-----------。
10. 将导线围成边长为a 的正三角形线圈,通电电流为I ,则三角形中心处的磁感应强度是----------。
三角形边长延长线上一点P 到角的距离为a ,P 点的磁感应强度是-----------。
11. 半径为R 的通电电流为I 的半圆弧导线在圆心处的磁感应强度是-------------。
长直螺旋管通有电流为I ,单位长度的线圈匝数为n ,内部充满磁导率为μ的磁介质,则其内部磁感应强度B=----------。
12. 电流密度为j 无限长均匀通电圆柱导线内一点到轴线距离为r ,该点的磁感应强度大小B=-----,方向----------,磁能密度m ω=----------。
13. 电子e 以速度v 绕原子核做圆周运动半径为R ,则电子的轨道磁矩是---------。
14. 磁矩为P m 的线圈处在匀强磁场中,最大磁力矩是----------,当线圈平面与磁场夹角为/3π时,磁力矩为-----------。
15. 按相对磁导率r μ的不同,把磁介质划分为:铁磁质--------,顺磁质--------,抗磁质-------。
(填写相对磁导率大小)16. 导线在磁场中运动切割磁力线,导线中有动生电动势,其非静电力是--------,非静电力场强k E =---------。
17. 涡旋电场与静电场的不同处是-------------------------------------------------------。
18. 自感系数为L 的线圈通电电流由I 变为3I 时,自感磁能变化为-----------。
19. 位移电流和传导电流都能激发磁场,来源本质不同:---------------------,------------------。
20. 电磁波的能量密度矢量称为坡印廷矢量S =-------------,其方向与电场、磁场的关系是------------------------。
21. 描述原子状态的四个量子数是----------、---------、--------、--------。
主量子数n 不同对应不同的壳层,n=3时,该壳层最多可容纳的电子数是--------,电子最大角动量为--------。
对于l =3,z L =-------------.22. 波函数的标准化条件有---------、--------、--------,归一化条件的表述为--------------------。
23. 对量子力学作出主要贡献的科学家有----------、--------、---------、--------、----------、-----------等,主要贡献是---------、----------、---------、----------、------------、------------。
24. 光电效应实验中,测定红限波长关系式------------------。
25. 康普顿散射解释的要点----------------------、---------------------------、结论----------------------。
26. 同时测量动能为5keV 的作一维运动的电子的位置与动量时,若位置的不确定值在0.3nm(1nm=10-9m)内,则动量的不确定值的百分比△P/P 至少为何值?27、一平行板电容器,充电后切断电源,然后使两极板间充满相对电容率为r ε的各向同性均匀电介质,此时两极板间的电场强度是原来的 倍;电场能量是原来的 倍。
28、平行板电容器其内充满介电常数为r ε的各向同性均匀电介质,充电后极板上的电荷面密度分别为σ±,忽略边缘效应,则介质中的场强应为 。
29、真空中静电场的高斯定理的数学表达式为 ,它说明了静电场是 场。
30、两个通有相等电流I 的圆线圈,半径均为R ,一个线圈水平放置,另一个线圈竖直放置,两圆心重合,则圆心处磁感应强度的大小B = 。
31、在如图所示的回路中,两共面半圆的半径分别为a 和b ,且有公共圆心O ,当回路中通有电流I 时,圆心O 处的磁感应强度B0= ,方向 。
32、一条长m 1的直导体棒沿Y 轴方向放置,通以电流A I 10=沿Y 轴正方向,导体棒所在处的磁场0.3 1.20.5()B i j k T =-+,则该导体棒所受的磁力F = ()N 。
33、法拉第电磁感应定律的一般表达式: ,式中负号的含义是: 。
34、无限长密绕直螺线管通有电流I ,内部充满均匀、各向同性的磁介质,磁导率为μ,管上单位长度绕有n 匝导线,则内部的磁感应强度为 。
35、一半径为R 的均匀带电圆环,电荷线密度为λ。
设无穷远处为电势零点,则圆环中心O 点的电势U 0= 。
36、将一个通有电流强度为I 的闭合回路置于均匀磁场中,回路所围面积的法线方向与磁场方向的夹角为a ,若均匀磁场通过此回路的磁通量为Ф,则回路所受力矩的大小为 。
37、均匀磁场B 限制在半径为R 的无限长圆柱形空间内,若磁场的变化率dt dB /为正的常数,则圆柱形空间外距轴线为r 的P 点处的感生电场i E 的大小为 。
38、无限长密绕螺线管单位长度上的自感为L ,若通过的电流I 增大,L ;若匝密度n 增大,L 。
(填增大、减小或不变)。
39、质量为m 的粒子以速度v 运动时,其德布罗意波的波长为 ,设普朗克常数为h.40、设描述微观粒子运动的波函数为(r , t ) 须满足的标准条件是 、 、 。
41、设描述微观粒子运动的波函数为(,)r t ,则﹡表示 ,其归一化条件是 。
42、根据量子力学理论,氢原子中电子的角动量在外磁场方向上的投影为Lz= l m ,当角量子数l =2时,L z 的可能取值为 。