测不准关系
- 格式:pptx
- 大小:207.16 KB
- 文档页数:8

南京师范大学泰州学院毕业论文(设计)( 2012 届)题目:院(系、部):专业:姓名:学号指导教师:南京师范大学泰州学院教务处制目录1.引言 (5)2、测不准关系的理论背景 (5)2.1 粒子的波动性 (5)2.2波的粒子性 (6)3.测不准关系式的简要导出 (7)3.1 由电子的单缝衍射导出测不准关系 (7)3.2由量子力学中的特例导出测不准关系式 (7)3.3由量子力学中的算符的对易关系导出测不准关系式 (7)3.4、由量子理论的基本假定直接导出测不准关系式。
(7)4 对测不准关系的认同与争议 (9)4.1对测不准关系的争议 (9)4.1.1统计解释与非统计解释 (9)4.1.2某些力学量测不准的原因是什么 (9)4.1.3关于名称和译名的争议 (10)4.2对有争议问题的讨论 (10)4.2.1关于统计解释和非统计解释 (10)4.2.2某些力学量测不准的原因 (11)4.2.3关于uncertainty和indeteminacy的译名问题 (11)5 测不准关系的应用 (11)5.1无限深势阱问题 (12)5.2 线性谐振子问题 (13)5.3 氢原子问题 (15)结语 (16)谢辞 (17)参考文献 (17)摘要测不准关系是量子力学的一个基本原理,表明一个微观粒子的某些成对的物理量不可能同时具有确定的数值,例如位置与动量、时间和能量。
它反映了自然界的客观规律, 反映了微观粒子的波粒二象性的基本属性。
本文主要介绍了测不准关系的理论背景,导出模式以及对测不准关系的认同与争议,重点讨论了测不准关系在量子力学上的应用。
通过无限深势阱、线性谐振子、氢原子等几个模型问题的基态能量的求解,证明了测不准关系在物理量大小估算问题上具有的应用意义和价值.关键词:测不准关系;量子力学;估算AbstractThe uncertainty relation is a fundamental principle of quantum mechanics. It showed that the value of a microscopic particle having certain pairs of physical quantities is not possible to determine, such as position and momentum, time and energy. It reflects the objective laws of nature, reflecting the basic properties of micro-particle wave-particle duality.This paper focuses on the application of uncertainty relation on quantum mechanics. Firstly, we make a detailed investigation regarding the theoretical background, export mode, and the recognition and controversy of uncertainty relation. Basing on the solution of several model problems such as the infinite potential well, linear harmonic oscillator, hydrogen atom ground state energy, it is necessary to be figured out that Uncertainty relation in the meaning and value on the physical size of the estimation problem.Keywords: Uncertainty relation ;quantum mechanics;estimation1.引 言测不准关系又名“测不准原理”、“不确定关系”,由海森伯在1927 年率先提出, 经历了大半个世纪争论,近30年来才逐渐取得一致, 成为量子力学的重要内容。

量子力学中的测不准关系量子力学是研究微观世界的物理学分支,它的出现彻底改变了我们对于自然界的理解。
在量子力学中,测量是一个核心概念,而测不准关系则是量子力学中重要的原理之一。
本文将探讨量子力学中的测不准关系,并解释其背后的物理原理。
一、测不准关系的定义在量子力学中,测不准关系也被称为海森堡不确定关系,它由物理学家维尔纳·海森堡于1927年提出。
测不准关系指的是当我们试图同时测量一个粒子的位置和动量时,无法同时获得它们的精确值,而只能得到一个不确定的范围。
换句话说,我们无法同时获得一个粒子的位置和动量的确切数值。
二、海森堡不确定原理为了更好地理解测不准关系,我们需要了解海森堡不确定原理。
海森堡不确定原理可以分为位置-动量不确定关系和能量-时间不确定关系两个方面。
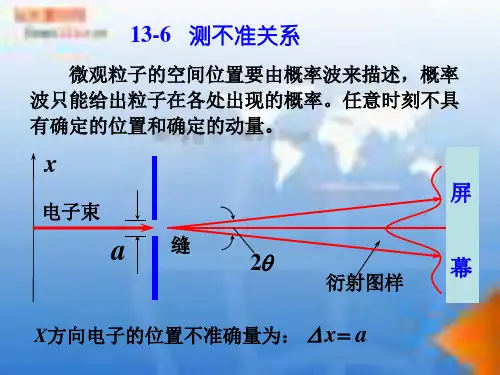
1. 位置-动量不确定关系根据位置-动量不确定关系,我们无法准确地同时知道一个粒子的位置和动量,其原理可以用数学表达式来描述:Δx·Δp ≥ h/(4π)其中,Δx表示位置的不确定度,Δp表示动量的不确定度,h为普朗克常数。
这个不等式告诉我们,当我们试图减小位置的不确定度时,动量的不确定度就会增加,反之亦然。
也就是说,如果我们越来越精确地知道一个粒子的位置,我们就越来越不确定它的动量,反之亦然。
2. 能量-时间不确定关系能量-时间不确定关系是海森堡不确定原理的另一个方面。
根据能量-时间不确定关系,我们无法准确地同时知道一个量子态的能量和持续时间,其原理可以用数学表达式来描述:ΔE·Δt ≥ h/(4π)其中,ΔE表示能量的不确定度,Δt表示时间的不确定度,h为普朗克常数。
这个不等式告诉我们,当我们试图减小能量的不确定度时,时间的不确定度就会增加,反之亦然。
也就是说,如果我们越来越精确地知道一个量子态的能量,我们就越来越不确定它的持续时间,反之亦然。
三、测不准关系的物理解释量子力学中的测不准关系并非是由于我们的测量工具或者技术的限制,而是与量子粒子的本质有关。

量子力学中的测不准关系量子力学是研究微观世界的基本物理理论,它描述了微观粒子的行为和性质。
而测不准关系是量子力学中的一个重要概念,它揭示了在测量某个物理量时的固有不确定性。
本文将介绍测不准关系的基本原理、相关数学表达式以及其在现实世界中的应用。
测不准关系的基本原理可以追溯到1927年由维尔纳·海森堡所提出的海森堡不确定性原理。
该原理指出,在任何时刻,无法同时准确测量一个粒子的位置和动量。
这意味着,如果我们试图确定粒子的位置,那么它的动量就将变得模糊不清;反之,如果我们试图确定其动量,其位置也将变得不确定。
换句话说,存在一个固有的不确定度,限制了我们在同一时间测量多个相关物理量的精确性。
测不准关系可以用数学表达式来描述。
以位置(x)和动量(p)的测量为例,海森堡不确定性原理给出了以下数学关系:Δx × Δp ≥ ħ/2其中,Δx代表位置的不确定度,Δp代表动量的不确定度,ħ是普朗克常量的约化值。
这个关系的意义是,位置和动量的不确定度的乘积不能小于普朗克常量的一半。
这说明了在微观尺度上,我们无法同时精确测量位置和动量。
值得一提的是,测不准关系并不是由于观测方法或仪器的限制,而是与量子粒子的本质有关。
这是因为在测量时,我们必须使用光子或其他粒子与被测系统相互作用,而这种相互作用必然会对被测系统的状态产生不可忽视的影响。
因此,测不准关系实际上揭示了微观粒子的固有性质。
测不准关系在实际应用中具有重要意义。
首先,它对于狭义相对论与量子力学的统一提供了重要的线索。
狭义相对论描述了高速运动下的物体,量子力学描述了微观尺度的物体。
然而,这两个理论之间的矛盾问题一直困扰着物理学家。
通过引入测不准关系,我们可以看到,测量的不确定性与时空观念的相对性密切相关,这为两个理论的统一提供了可能性。
其次,测不准关系在量子信息科学、量子计算和量子通信等领域也有广泛应用。
在量子计算中,信息的存储和处理是通过量子比特来实现的。

量子力学中的不确定性原理与测不准关系量子力学是描述微观世界的一门物理学理论,它与经典力学有着本质的不同。
在量子力学中,不确定性原理和测不准关系是两个重要的概念,它们揭示了微观粒子的本质和测量的局限性。
本文将从不确定性原理和测不准关系的定义、物理背景和实际应用等方面进行探讨。
不确定性原理是量子力学的核心概念之一,由德国物理学家海森堡于1927年提出。
它表明,在量子力学中,无法同时准确测量一个粒子的位置和动量。
换句话说,我们无法同时知道一个粒子的位置和速度,只能通过测量其中一个属性来获得信息。
这与经典力学中的观念不同,经典力学认为粒子的位置和速度是同时确定的。
不确定性原理的数学表达方式是海森堡不等式,即ΔxΔp ≥ h/4π,其中Δx表示位置的不确定度,Δp表示动量的不确定度,h为普朗克常数。
该不等式表明,位置和动量的不确定度的乘积不小于一个常数。
这意味着,我们无法将位置和动量的不确定度同时降到零,存在一种固有的测量局限性。
不确定性原理的物理背景可以从波粒二象性理论来解释。
根据波粒二象性理论,微观粒子既可以表现出粒子性,也可以表现出波动性。
当我们试图测量粒子的位置时,我们必须使用光子或其他粒子与待测粒子相互作用,这种相互作用会使待测粒子的位置发生扰动。
同样地,当我们试图测量粒子的动量时,我们必须使用波长足够小的粒子来进行测量,这样才能准确测量动量。
这种测量的过程会导致动量的不确定度增大。
因此,不确定性原理可以看作是波粒二象性理论的一个直接推论。
测不准关系是不确定性原理的一种具体应用。
它描述了在量子力学中,两个不可观测量的测量结果之间存在的一种固有的关系。
以位置和动量为例,根据测不准关系,我们无法同时准确测量一个粒子的位置和动量。
这是因为位置和动量是量子力学中的共轭变量,它们之间存在一种固定的关系。
当我们试图减小位置的不确定度时,动量的不确定度必然增大,反之亦然。
这意味着,我们无法完全确定一个粒子的位置和动量,只能通过测量其中一个属性来获得信息。

测不准关系的名词解释测不准关系(Heisenberg Uncertainty Principle),是量子力学中的一个基础定理,揭示了测量物质微观粒子位置和动量的限制。
这一原理由德国物理学家维尔纳·海森堡于1927年提出,对于当代科学研究和技术发展有着深远影响。
量子力学是描述微观世界行为的物理学理论,与经典物理学的牛顿力学相比,它具有离奇和令人难以理解的特性。
测不准关系正是其中一个最为重要的特征,它限制了我们对于粒子的位置和动量的准确测量。
首先,让我们来了解一下测不准关系的具体表述。
根据海森堡的提出,测不准关系公式可以表示为:Δx·Δp ≥ h/4π,其中Δx代表位置的不确定度,Δp代表动量的不确定度,h为普朗克常数。
这个公式告诉我们,在同一时间内,粒子的位置和动量不能同时被准确测量,它们之间存在一种固有的不确定性。
为了更好地理解测不准关系,我们可以用一个简单的例子来说明。
假设有一颗微小的粒子在一个无限深势阱中运动。
如果我们希望测量它的位置,我们可以用光子照射它,并测量光子在接收器上的位置。
然而,当光子与粒子相互作用时,光子传递给粒子的动量必然会对粒子的位置产生影响。
这意味着,我们无法同时确定粒子的位置和动量。
测不准关系的存在不仅仅是技术上的限制,它也揭示了物质微观粒子本质上的模糊性和不确定性。
在经典物理学中,我们通常认为物体的位置和动量是可以准确测量的,但在量子力学中,我们必须接受事物的这种局限。
测不准关系不仅仅是学术领域的理论问题,它也在实际应用中具有广泛的意义。
例如,在核能的开发中,测不准关系的概念帮助我们理解原子核的性质和结构。
在纳米技术和量子计算领域,测不准关系的限制也对制造和测量微小物体的设备有着重要影响。
除了这些应用外,测不准关系还引发了哲学上的思考。
它挑战了我们对物质世界的看法,让我们意识到自然界的本质并非完全确定和可预测的。
这一思想深入人心,推动了科学研究对于个体和整体之间相互关系的探索。


不确定关系(测不准关系)的表述和含义摘要:介绍了测不准关系的一些不同的表述和证明方法,对其中关于这一原理的认同和有争议的问题进行了比较与分析。
关键词:测不准关系;不确定度;量子理论;统计解释引言测不准关系是由量子力学基茌原理导出的一个重要推论,它是量子力学的一个基本原理,表明一个微观粒子的某些成对的物理量不可能同时具有确定的数值,例如位置与动量、时间和能量。
它反映了自然界的客观规律, 反映了微观粒子的波粒二象性的基本属性它在量子力学中占有重要的地位。
量子力学诞生至今约有80年了,作为一门基础理论已经相当成熟,在指导人类文明进步和学科发展方面发挥着重要的作用;但是,对量子力学基本理论的解释却一直存在着不同意见的争论,关于测不准关系的理解问题是争论的焦点之一。
本文对其中一些主要的有争议问题进行简要的介绍,并加以讨论。
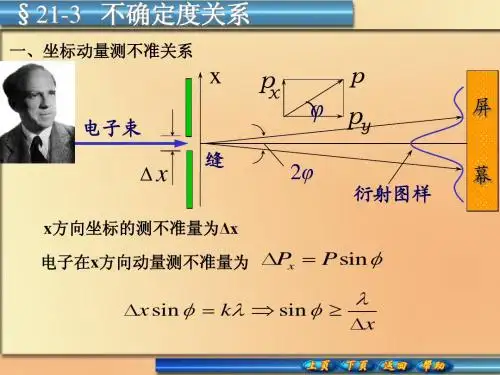
1 几种主要的表述和证明方法测不准关系是海森堡在1927年提出的,他设想一种使用波长很短的γ射线的显微镜来最大限度地精确测定电子的位置,这种测量,依靠的是光子被电子的散射[康普顿(compt)散射。
海森堡在题为“关于最子理论的动力学和力学的直观内容”的论文中说[1]:“当测定…电子‟位置的瞬间,也正是光产被电子散射的瞬问,电子的动量产生一个不连续的改变。
当所用的光的波长越小,即位置测定得越精确,这一改变就越大。
因此,在知道电子位置的瞬间,它的动量只能了解到对应于那一不连续改变的大小的程度。
于是,位置测定得越精确,动量就知道得越不精确,反之亦然。
在这种情况下,我们看到方程pq—qp=-ih的一种直接的物理解释。
这就是在文献中第一次出现的关于测不准关系的表述。
1929年,罗伯逊(Robertson)[2]在一篇短文中首次证明:两个厄密算符的标准偏差之积绝不会小于它们的对易子的平均的绝对值之半。
证明如下:设A和B是任意的两个厄密算符,C是它们的对易子,令A1=A一<A>,B1=B 一<B>,A和B的标准偏差分别为△A=<A12>1/2和△B=<B12>1/2。

不确定关系测不准关系的表述和含义Document serial number【LGGKGB-LGG98YT-LGGT8CB-LGUT-不确定关系(测不准关系)的表述和含义摘要:介绍了测不准关系的一些不同的表述和证明方法,对其中关于这一原理的认同和有争议的问题进行了比较与分析。
关键词:测不准关系;不确定度;量子理论;统计解释引言测不准关系是由量子力学基茌原理导出的一个重要推论,它是量子力学的一个基本原理,表明一个微观粒子的某些成对的物理量不可能同时具有确定的数值,例如位置与动量、时间和能量。
它反映了自然界的客观规律, 反映了微观粒子的波粒二象性的基本属性它在量子力学中占有重要的地位。
量子力学诞生至今约有80年了,作为一门基础理论已经相当成熟,在指导人类文明进步和学科发展方面发挥着重要的作用;但是,对量子力学基本理论的解释却一直存在着不同意见的争论,关于测不准关系的理解问题是争论的焦点之一。
本文对其中一些主要的有争议问题进行简要的介绍,并加以讨论。
1 几种主要的表述和证明方法测不准关系是海森堡在1927年提出的,他设想一种使用波长很短的γ射线的显微镜来最大限度地精确测定电子的位置,这种测量,依靠的是光子被电子的散射[康普顿(compt)散射。
海森堡在题为“关于最子理论的动力学和力学的直观内容”的论文中说[1]:“当测定‘电子’位置的瞬间,也正是光产被电子散射的瞬问,电子的动量产生一个不连续的改变。
当所用的光的波长越小,即位置测定得越精确,这一改变就越大。
因此,在知道电子位置的瞬间,它的动量只能了解到对应于那一不连续改变的大小的程度。
于是,位置测定得越精确,动量就知道得越不精确,反之亦然。
在这种情况下,我们看到方程pq—qp=-ih的一种直接的物理解释。
这就是在文献中第一次出现的关于测不准关系的表述。
1929年,罗伯逊(Robertson)[2]在一篇短文中首次证明:两个厄密算符的标准偏差之积绝不会小于它们的对易子的平均的绝对值之半。
第五章 测不准关系第一部分 内容提要一 体系处于力学量的本征态吓测量力学量时,测量值就是态的本征值,有唯一确定值,几率是1。
二 如果两个力学量相互对易,则它们有共同本征态.在它们共同本征态中测量两个力学量分别有确定值。
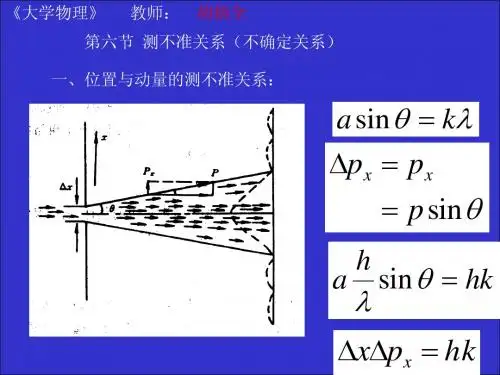
三 如果两个力学量算符Fˆ和G ˆ不对易: 0ˆ]ˆ,ˆ[≠=K i G F 则在体系的任意状态),(t rψ 下测量F 和G 不能同时测准。
记 τψ-ψ=-=∆⎰d F F F FF )ˆ()ˆ()(* τψ-ψ=-=∆⎰dG G G GG )ˆ()ˆ()(* 可以证明:2)()(22K G F ≥∆⋅∆特别地有:2)()(22≥∆⋅∆p x四 利用经典力学和测不准关系修正可以估算量子体系地能级,尤其是基态能级。
第二部分 例题讲解例题1 试证明测不准关系式。
已知 0ˆ]ˆ,ˆ[≠=K i G F则 2)()(22K G F ≥∆⋅∆证明:考虑下列积分0ˆˆ)(2≥τψ+ψξ=ξ⎰d G i FI ψ为体系任一波函数,ξ为任一实参数。
利用算符Fˆ和G ˆ的厄米性以及ξ为实数,上面不等式左边可写为:τψ+ξ+ξψ=τψ+ψξψ+ψξ=ξ⎰⎰d G i F G i F d G i F G i FI ]ˆˆ[]ˆˆ[]ˆˆ[]ˆˆ[)(*** τψ-ξ++ξψ=τψ+ξ-ξψ=⎰⎰d G F G F i GF dG i F G i F]ˆˆˆˆ(ˆˆ[]ˆˆ][ˆˆ[222**=K i G F G Fi G F ξ++ξ=ξ++ξ222222]ˆ,ˆ[ = 0)4()2(222222≥-+-ξFK GFK F不妨取实参数 22FK =ξ 则 0)4(222≥-FK G所以 222K F G ≥⋅或]ˆ,ˆ[2122G F FG ≥⋅ 简记为]ˆ,ˆ[21G FG F ≥∆⋅∆ 例题二 质量为m 、速度为V 、能量为221mv E =的粒子沿x 轴方向运动,其位置的测量误差为x ∆,设v x t /∆=∆,试由测不准关系 21≥∆∆p x ,导出能量与时间的测不准关系:21≥∆∆t E解: 因为mv p = 所以 v m p ∆=∆ 又221mv E =得tx p pv v mv E ∆∆∆=∆=∆=∆则 21≥∆∆=∆∆x p t E例题三 试利用测不准关系估算[1] 氢原子的基态能级,设rempH22412ˆπε-=[2] 类氢离子得基态能,其中:rze c m c p H221422241)(ˆπε-+=解: [1] 按经典力学观点氢原子能量是rempE 22412πε-=,由于经典力学中r 和p 可以同时确定,即允许0,0=∆=∆p r ,于是0=r 且p=0时氢原子能量最低(∞-),这显然不符合实验事实。
测不准原理的深刻内涵测不准原理,又称海森堡测不准关系,是量子力学中的一个基本原理,由德国物理学家海森堡于1927年提出。
该原理指出,在微观粒子的测量过程中,无法同时准确确定粒子的位置和动量,即在某一时刻对粒子位置的测量精度越高,对其动量的测量精度就越低,反之亦然。
这一原理揭示了微观世界的不确定性,深刻影响着量子力学的发展和人们对自然界的认识。
测不准原理的内涵之一在于揭示了自然界的基本规律是不确定的。
在经典物理学中,人们习惯于用确定性的观念来描述物体的运动状态,认为只要掌握了物体的位置和速度,就可以准确预测其未来的运动轨迹。
然而,测不准原理的提出打破了这种观念,表明在微观世界中,粒子的位置和动量并不存在同时确定的可能性,这种不确定性是量子世界的固有属性。
因此,测不准原理的深刻内涵之一是让人们意识到,自然界并非完全可预测,存在着一定的随机性和不确定性。
另一个深刻内涵是测不准原理揭示了观察者与被观察对象之间的相互影响。
在经典物理学中,人们往往认为观察者可以客观地观测物体的状态,而不会对物体本身造成影响。
然而,量子力学的测不准原理表明,观察者的测量行为会对微观粒子的状态产生影响,甚至改变其原本的运动状态。
这种观察者效应引发了人们对于客观性和主观性的思考,提出了“观察即塑造”这一新的认识观念,拓展了人们对于观察与实验的理解。
此外,测不准原理还启示人们对于信息获取的局限性。
根据测不准原理,粒子的位置和动量无法同时被准确测量,这意味着存在着信息的缺失和不完全性。
在量子世界中,信息的获取受到一定的限制,无法获得完整和准确的信息。
这种信息的局限性不仅影响了科学研究的深入,也引发了人们对于信息论和量子通信等领域的探讨,推动了信息科学的发展。
总的来说,测不准原理的深刻内涵包括揭示了自然界的不确定性、观察者效应以及信息获取的局限性。
这一原理的提出不仅拓展了人们对于量子世界的认识,也引发了对于科学哲学和认识论的思考。
通过深入探讨测不准原理的内涵,可以更好地理解量子力学的基本原理,拓展人们对于自然规律的认识,推动科学技术的发展。