大学物理,量子物理基础21-05测不准关系

测不准原理的应用1. 介绍测不准原理（Uncertainty Principle）是量子力学中一个重要的基本原理，也被称为海森堡不确定性原理。

它由德国物理学家维尔纳·海森堡于1927年提出，指出在对粒子位置和动量进行测量时，由于测量的干扰，无法同时准确地确定粒子的位置和动量。

该原理揭示了微观世界的本质限制，具有深远的物理意义。

不仅如此，测不准原理也被广泛应用于各个领域，如量子信息、量子计算、精密测量等，为科学研究和技术发展带来了重要的启示和应用。

2. 测不准原理的表述测不准原理表述了量子系统中位置和动量的测量精度之间的不可避免的一个关系。

具体而言，对于一个处于确定状态的量子粒子，其位置和动量的测量结果无法同时具有无限的精度。

换句话说，无论使用任何精确的测量仪器和方法，存在一个测量误差限制，使得位置和动量的测量结果不能同时达到无限精确。

3. 测不准原理在量子信息中的应用3.1 量子通信测不准原理在量子通信中具有重要的应用价值。

量子通信是一种基于量子态传输的通信方式，具有高度的安全性和抗干扰性。

根据测不准原理的原理，发信方可以将信息编码成量子态，并通过测量对量子态进行解码。

由于测量过程的干扰，窃听者无法准确获取量子态的信息，保证了通信的安全性。

基于测不准原理的量子通信已经在很多领域得到成功应用，例如量子密钥分发、量子加密等。

3.2 量子计算测不准原理在量子计算中也有重要的应用。

量子计算是一种基于量子力学原理的计算方式，可以在某些情况下实现比传统计算机更快的计算速度。

测不准原理指出了测量过程对量子系统状态的干扰，这对量子计算提出了限制。

在量子计算过程中，需要通过量子门和量子比特的操作来实现特定计算任务，而测不准原理的存在则要求我们对量子比特的位置和动量进行精确控制，以避免干扰和误差的累积。

因此，测不准原理为我们设计和实现高效的量子计算提供了重要的指导。

4. 测不准原理在精密测量中的应用测不准原理在精密测量领域也有广泛的应用。

物本1201班第一小组潘荣杰，聂姝，吕舒鹏，朱建宇，韩娟，王金凤，弥倩琴，王震，张毛毛，吴松伟测不准原理测不准原理是误译，更严格的叫法是不确定关系。

只是在描述时用了波的描述而不是用的粒子描述，对其本身的解释并不需涉及观测。

量子论就是采用波函数的观点，以薛定谔方程为假设（注意是假设，就像狭义相对论的两条基本假设一样）来构建的一个理论体系，然后它能解释实验。

不确定关系简单点说是：由波函数确定的一个物理对象，对其某个力学量描述本身就会弥散（比如你要说一个波在空间什么位置，其他力学量同理，当然，不考虑处在力学量本征态的情况），两个力学量弥散的程度满足不确定关系。

观测的问题是量子论年代久远而尚未得到解决的问题，一般常见的解释是波函数的塌缩。

也就是在测量前，系统可能处在某个力学量的本征态或者几个本征态的叠加态上，当我们对这个力学量进行测量时，波函数将塌缩到测量值所对应的本征态上（但是，一般认为，任何一个（或者说绝大多数）力学量的本征态都是完备的，可以构成希尔伯特空间的一组基，对于测量所得到的力学量本征态而言，其对其他力学量来说可能是叠加态）这是观测对系统施加的影响。

是观测将一个可能态变成另一个可能态。

而不确定关系是，即使不施加观测，对于处在一个态中的粒子，它的力学量也将满足不确定性关系。

不确定关系中的ΔAΔB(常见点用动量－位置就是ΔpΔx)不是指观测值与实际值的偏差，而是指力学量的统计方差平方根（如果您学过统计，波函数实际确定了力学量值的分布概率，就知道由此可以完全通过统计方法的求出方差而不用通过测量）量子力学如果根基有什么不稳定的话，在于波函数的塌缩解释而不在于不确定关系。

测不准原理来源于物质的二象性。

既是微粒，又是波，这是微观物体表现出来的性质，所以测不准原理是物质的客观规律，不是测量技术和主观能力的问题。

量子力学中的不确定关系理论量子力学是描述微观物理世界的一种理论，它揭示出了一系列与经典物理完全不同的现象和规律。

其中最重要的之一就是不确定关系理论，也被称为海森堡不确定性原理。

不确定关系理论是在量子力学中，认为存在一种不可能同时准确测量位置和动量的限制。

具体来说，对于一个粒子的位置和动量两个物理量，无法同时准确测量它们的值，即精确地同时知道一个粒子的位置和动量是不可能的。

海森堡不确定性原理的基本形式是：Δx · Δp ≥ h/2π其中，Δx表示位置的不确定度，Δp表示动量的不确定度，h为普朗克常数。

这一原理的含义是，如果我们试图减小对粒子位置的不确定性，那么对其动量的不确定性就会增加；反之亦然。

换句话说，粒子的位置和动量之间存在一种固有的关联，我们无法通过任何手段消除这种关联的存在。

不确定关系理论的提出，对于量子力学的发展具有重大的影响。

它挑战了经典物理学中的确定性观念，揭示了微观世界的本质特征。

不确定关系理论不仅适用于位置和动量的测量，还适用于其他一些共轭物理量的测量，比如时间和能量、角度和角动量等。

不确定关系的原理是基于量子物理的波粒二象性的理论基础。

在量子力学中，粒子既可以被看作是传统的粒子，也可以被看作是波动的能量。

而不确定关系的出现正是由于粒子既具有粒子性又具有波动性。

从宏观世界的角度看，我们可以很容易地测量物体的位置和动量，而且这两个量之间的关系是明确、可测的。

然而，在微观世界中，粒子的位置和动量却无法同时准确确定。

这是因为我们不能像经典物理学中那样，通过测量物体的位置和速度来准确确定其动量。

不确定关系的存在给实验物理学带来了挑战。

在进行微观世界的实验时，我们往往要面对因为测量位置而干扰了动量的测量，或者因为测量动量而干扰了位置的测量。

这种不确定性不仅仅是技术上的限制，而是由量子力学的本性所决定的。

尽管不确定关系理论使我们无法同时准确测量位置和动量，但它并不意味着我们对微观世界一无所知。

量子测量与测量不确定性引言：量子力学是描述微观世界行为的理论，而测量是量子力学中不可或缺的一部分。

量子测量是指通过实验手段来获取粒子的某些性质的过程。

然而，与经典物理学不同的是，量子测量存在着不确定性，即无法准确预测测量结果。

本文将深入探讨量子测量的原理和测量不确定性的概念。

一、量子测量的原理在经典物理学中，测量是指通过观察物体的状态来确定其性质。

然而，在量子力学中，测量是一个复杂的过程，涉及到波函数的坍缩和测量结果的随机性。

1. 波函数坍缩根据量子力学的基本原理，一个粒子的状态可以用波函数来描述。

波函数是一个复数函数，包含了粒子的所有可能状态。

当进行测量时，波函数会发生坍缩，即从多个可能状态中随机选择一个状态。

这个过程是不可逆的，一旦测量结果确定，波函数就会坍缩到对应的状态上。

2. 测量结果的随机性在量子力学中，测量结果是随机的，无法准确预测。

即使在相同的实验条件下，重复进行测量，也会得到不同的结果。

这是因为在测量过程中，波函数坍缩到不同的状态上的概率是不确定的。

只能通过统计的方法来描述测量结果的分布。

二、测量不确定性的概念测量不确定性是指在量子测量中，无法同时准确确定粒子的多个物理量。

根据量子力学的不确定性原理，对于一对不可对易的物理量，比如位置和动量，无法同时准确测量它们的值。

1. 测量不确定性原理根据海森堡的测量不确定性原理，对于一对不可对易的物理量A和B，它们的测量结果的标准差满足以下关系：ΔAΔB ≥ ħ/2，其中ΔA和ΔB分别是物理量A和B的标准差，ħ是普朗克常数的约化常数。

这个原理表明，当我们尝试减小一个物理量的测量不确定性时，另一个物理量的测量不确定性会增大。

这是量子世界中的一种固有的限制，与经典物理学中的测量精确度没有可比性。

2. 应用举例：位置和动量的不确定性位置和动量是量子力学中最基本的物理量之一，它们之间存在着测量不确定性。

根据测量不确定性原理，我们无法同时准确确定粒子的位置和动量。

测不准原理的应用及意义1、测不准原理的定义及理论背景1.1 测不准原理的定义测不准原理由量子力学创始人德国物理学家海森堡于1927年提出,又名“不确定关系”,英文"Uncertainty principle",是量子力学的一个基本原理,本身为傅立叶变换导出的基本关系:若复函数与构成傅立叶变换对,且已由其幅度的平方归一化(即相当于的概率密度相当于的概率密度,‘’表示复共轭),则无论的形式如何,与标准差的乘积不会小于某个常数(该常数的具体形式与的形式有关)。

1.2 测不准原理的理论背景测不准原理是物质世界的一个基本的不可回避的性质,人们习惯于对物体运动轨迹的准确描述,大到天体如何运行,小到微尘如何飞扬。

这种认识必须基于对物体能够准确定位。

为了预测一个物体的运动状态,必须准确测量它的位置和速度。

测定必须施加一个物理量作用于作为被测对象的物体之上,这在任何一种测量中都无法幸免。

显然,对在微观粒子尺度空间的测量方法用光照最合适。

然而,光照是无法把粒子的位置确定到比光的波长更小的程度的。

为了测定的准确,必须用更短波长的光,这意味着光子的能量更高,这样测定对粒子速度的扰动将很厉害。

因此,不能同时准确的测定粒子的位置和速度。

事实上,宏观世界和微观世界都受到测不准原理的制约,只不过对宏观物体的测量,一定波长的光已经足够精确,且扰动对其速度的影响小到远远无法计较。

测不准原理揭示了微观粒子运动的基本规律:粒子在客观上不能同时具有确定的坐标位置及相应的动量。

如果微观粒子的位置的不确定范围是,同时测得的微粒的动量的不确定范围是。

与的乘积总是大于。

这里,为普朗克Plank常数。

测不准原理来源于微观粒子的波粒二象性,是微观粒子的基本属性,所谓的测不准与测量仪器的精度无关。

1.2.1 海森伯海森伯在创立矩阵力学时,对形象化的图象采取否定态度。

但他在表述中仍然需要使用“坐标”、“速度”之类的词汇,当然这些词汇已经不再等同于经典理论中的那些词汇。

量子力学中的不确定性原理与测量量子力学是20世纪最重要的科学理论之一，它深刻地改变了人们对于自然界的认识。

在量子力学中，不确定性原理是一项基本原理，它揭示了微观粒子的本质和行为。

本文将探讨量子力学中的不确定性原理与测量的关系。

不确定性原理最早由德国物理学家海森堡于1927年提出，它包含了两个方面的不确定性：位置-动量不确定性原理和能量-时间不确定性原理。

位置-动量不确定性原理指出，对于一个粒子的位置和动量，我们无法同时精确地确定它们的值。

换句话说，我们不能同时知道一个粒子的位置和速度。

这个原理的意义在于，它限制了我们对于微观世界的认知能力。

在测量一个粒子的位置时，我们会扰动它的动量，因此我们无法同时准确地知道它的位置和动量。

能量-时间不确定性原理则揭示了能量和时间的不确定性。

根据这个原理，我们无法同时确定一个粒子的能量和它的存在时间。

这是因为测量一个粒子的能量会导致它的存在时间变得不确定。

这个原理的意义在于，它限制了我们对于微观世界的时间观测能力。

我们无法精确地知道一个粒子存在的时间，并且存在时间越短，能量就越不确定。

不确定性原理的提出引起了物理学界的广泛争议和讨论。

有些人认为不确定性原理只是一种测量误差，而并非真正的本质不确定性。

然而，随着实验证据的积累，不确定性原理已经被广泛接受，并且成为了量子力学的基本原理之一。

测量在量子力学中起着重要的作用。

在经典物理学中，测量被认为是确定性的，即通过测量我们可以准确地得到一个物理量的值。

然而，在量子力学中，测量不再是确定性的。

根据量子力学的观点，测量会引起系统的塌缩，使得系统处于某个确定的状态。

这个塌缩过程是随机的，无法预测。

因此，我们无法准确地预测一个粒子在测量之前的状态。

测量的不确定性与不确定性原理密切相关。

根据不确定性原理，我们无法同时准确地测量一个粒子的位置和动量，或者能量和时间。

这意味着，我们在测量一个物理量时，必然会引入一定的不确定性。

我们只能得到一个概率分布，而不是一个确定的值。

课程论文学院：物理电子工程学院专业：物理学年级： 2012级物理学班*名：***论文题目：测不准关系的理论推导成绩：2016 年 1 月 2 日目录摘要 (1)Abstract (1)1.引言 (1)2.历史发展 (1)3.测不准关系实验验证 (3)4.相关质疑 (3)5.意义 (4)5.1理论意义 (4)5.2现实意义 (4)6.总结 (4)参考文献 (4)测不准关系的理论推导学生姓名：李赵坤学号：20125041015学院：物理电子工程学院专业：物理学摘要：在量子力学里，测不准关系表明，粒子的位置与动量不可同时被确定，位置的不确定性与动量的不确定性遵守不等式。

一个微观粒子的某些物理量，如位置和动量，或方位角与动量矩，还有时间和能量等，不可能同时具有确定的数值，其中一个量越确定，另一个量的不确定程度就越大。

关键词：波粒二象性，不确定原理1引言测不准原理，又称“不确定性原理”、“不确定关系”，是量子力学中的一个重要关系，也是一个相当深奥的问题[1]。

表明粒子的位置与动量不可同时被确定，它反映了微观客体的特征。

即一个微观粒子的某些成对的物理量不可能同时具有确定的数值。

例如位置与动量、力一位角与角动量，其中一个量越确定，另一个量就越不确定。

它来源于物质的波粒二象性，测不准关系是从粒子的波动性中引出来的。

2历史发展1900年普朗克为了解释黑体辐射的实验规律提出能量量子化的概念；1905年爱因斯坦为了解释光电效应引入光子的概念；1913年玻尔提出的氢原子理论中运用光子概念构造了频率条件；1923年，德布罗意提出物质波假设：实物粒子与光相似，也具有波粒二象性。

1925年6月，维尔纳·海森堡发表论文《运动与机械关系的量子理论重新诠释》创立了矩阵力学。

旧量子论渐渐式微，现代量子力学正式开启[2]。

海森堡在论文里提出，只有在实验里能够观察到的物理量才具有物理意义，才可以用理论描述其物理行为。

海森堡抓住云室实验中观察电子径迹的问题进行思考。

为什么量子力学的测不准原理叫原理而不叫定理或公式？
这是历史原因造成的。

现在大家通常将它叫做「不确定关系」，而已经不叫作「测不准原理」了。

在量子力学被发现的历史上，所谓的「测不准原理」曾经有很重要的地位，它由德国物理学家海森堡于1927年提出，这里的「原理」一次在英文中是principle，在海森堡最初提出这一原理的时候，它是作为某种「原理」存在的。

这种物理学上的「原理」其实类似于数学中的「公理」的地位。

然而，随着量子力学的发展，一个公理化的体系被建立起来，虽然这种「公理化」跟真正意义上的数学公理的那种严格有一定的差距，但仍然可以看成是一个很大的突破。

在狄拉克的《量子力学原理》中，注意狄拉克用的词就是principle，量子力学的基础被归纳为四个基本的公设，例如第一条，叠加原理，它也是被叫做「原理」的。

在狄拉克的量子力学框架下，不确定关系（或者测不准原理）已经不再是一条独立的原理，而是「对易关系」的一个推论，所以，我们现在其实可以说，不确定关系已经几乎可以看成是也有一个「定理」了。

其实在很多数学教科书中，在介绍傅里叶变换的性质时，也会讨论不确定关系，并且也是以定理的形式来证明的。

另外，需要补充的是，对于「能量—时间不确定关系」，由于「时间」在量子力学中不是一个可测量的物理量，所以，「对易关系」和「不确
定关系」之间不能完全重合。

量子力学中的测量问题与不确定性原理量子力学是描述微观世界的理论，它与经典物理学有着本质的不同。

在量子力学中，测量问题与不确定性原理是两个重要的概念，它们揭示了微观粒子行为的奇异性。

测量问题是指在量子力学中，测量结果的不确定性。

在经典物理学中，测量一个物理量时，我们可以准确地得到它的值。

然而，在量子力学中，测量结果却是不确定的。

这是因为在测量之前，粒子的状态是一个叠加态，即处于多个可能的状态之间。

当我们进行测量时，粒子会坍缩到其中一个确定的状态上，但我们无法预测它会坍缩到哪个状态上。

这种不确定性被称为量子力学的测量问题。

不确定性原理是由著名的物理学家海森堡提出的。

它指出，在量子力学中，存在着一种不可逾越的不确定性。

不确定性原理可以分为位置-动量不确定性原理和能量-时间不确定性原理两个方面。

位置-动量不确定性原理指出，我们无法同时准确地知道一个粒子的位置和动量。

如果我们测量一个粒子的位置，那么它的动量就变得不确定；反之亦然。

这是因为在量子力学中，位置和动量是相互关联的，它们不能同时具有确定的值。

这种不确定性限制了我们对粒子位置和动量的精确测量。

能量-时间不确定性原理指出，我们无法同时准确地知道一个粒子的能量和测量时间。

如果我们测量一个粒子的能量，那么它的测量时间就变得不确定；反之亦然。

这是因为在量子力学中，能量和时间也是相互关联的，它们不能同时具有确定的值。

这种不确定性限制了我们对粒子能量和测量时间的精确测量。

测量问题与不确定性原理的存在使得量子力学具有了一种新的解释方式。

在经典物理学中，我们可以通过精确测量来预测物体的运动和性质。

然而，在量子力学中，我们只能通过概率来描述粒子的行为。

这意味着，我们无法准确地预测粒子的运动和性质，只能给出它们出现在某个状态的概率。

这种概率性的描述是量子力学的核心特征。

测量问题与不确定性原理的研究对于理解微观世界的本质和发展量子技术具有重要意义。

通过对测量问题的研究，我们可以更好地理解量子系统的行为，并且为量子计算和量子通信等领域的发展提供理论基础。

量子力学的测不准原理与相干性效应的关系量子力学是描述微观世界行为的理论框架，而测不准原理和相干性效应是其中两个重要的概念。

本文将探讨量子力学的测不准原理与相干性效应之间的关系。

首先，让我们先了解一下测不准原理和相干性效应的概念。

测不准原理，也被称为海森堡不确定性原理，是量子力学中的基本原理之一。

它指出，在某些物理量的测量中，存在着不可避免的不确定性。

换句话说，无法同时准确地测量出一个粒子的位置和动量，或者同时准确地测量出一个粒子的能量和时间。

相干性效应，指的是量子态之间存在相应的干涉效应。

在量子力学中，粒子可以处于叠加态，即同时具有多个可能的状态。

当两个或多个叠加态发生干涉时，我们观察到的结果将受到相干性的影响。

在光学中，干涉现象就是一个常见的例子，可以观察到明暗相间的干涉条纹。

测不准原理和相干性效应之间的关系可以通过一种思想实验来理解，即著名的双缝干涉实验。

在这个实验中，我们通过一个狭缝让光通过，然后让这束光通过两个紧邻的狭缝，最后观察光在屏幕上的分布情况。

首先，假设我们能够完全测量光的入射位置和动量。

根据测不准原理，我们无法同时准确地测量出光的位置和动量，因此，我们无法确定光究竟是从哪一个狭缝通过的。

这就造成了我们观察到的结果无法解释的现象，即出现了明暗相间的干涉条纹。

其次，如果我们完全知道光的入射位置和动量，并且光通过的是某一个狭缝，那么我们可以确定观察到的分布情况。

但是，当我们无法确定光从哪一个狭缝通过时，光就变成一个叠加态，同时通过两个狭缝，并且会产生干涉效应。

这种叠加态的现象正是相干性效应的表现。

通过上述思想实验，我们可以看到测不准原理与相干性效应之间的密切关系。

测不准原理限制了我们对粒子位置和动量的同时精确测量，而相干性效应则是叠加态中不同可能状态之间的干涉。

两者共同作用下，我们观察到的结果具有一定的随机性和不确定性。

此外，测不准原理和相干性效应不仅仅在光学领域中有应用，它们在量子力学中的其他领域也发挥着重要作用。

量子力学中的测量与不确定性原理量子力学是现代物理学的重要分支，它描述了微观世界中粒子的行为和相互作用。

在量子力学中，测量是一个基本概念，它涉及到观察和确定粒子的性质。

然而，量子力学中存在着著名的不确定性原理，它限制了我们对粒子的测量精度。

本文将探讨量子力学中的测量与不确定性原理，并解释其背后的原理和应用。

首先，我们来了解一下测量在量子力学中的意义。

在经典物理中，我们可以通过测量来准确地确定物体的位置、速度和其他性质。

然而，在量子力学中，情况并非如此。

根据量子力学的原理，粒子的性质并不是事先确定的，而是存在于一个模糊的状态中，被描述为波函数。

当我们进行测量时，波函数将塌缩到一个确定的状态，这个状态对应着我们所观察到的粒子的性质。

然而，量子力学中的不确定性原理告诉我们，我们无法同时准确地确定粒子的多个性质。

最著名的不确定性原理是海森堡不确定性原理，它表明我们无法同时准确地确定粒子的位置和动量。

具体而言，海森堡不确定性原理给出了一个关系式：ΔxΔp ≥ h/4π，其中Δx表示位置的不确定度，Δp表示动量的不确定度，h为普朗克常数。

这个不确定性原理的意义在于，当我们试图减小位置的不确定度时，动量的不确定度将会增大；反之亦然。

这意味着我们无法同时精确地确定粒子的位置和动量。

这并不是因为我们的测量工具不够精确，而是因为量子力学本身的固有性质。

除了海森堡不确定性原理，量子力学中还存在着其他的不确定性原理。

例如，能量-时间不确定性原理告诉我们，我们无法同时准确地确定粒子的能量和时间。

这个不确定性原理的表达式为：ΔEΔt≥ h/4π，其中ΔE表示能量的不确定度，Δt表示时间的不确定度。

不确定性原理的存在对于我们的实验和观测有着重要的影响。

它告诉我们，我们无法完全确定粒子的性质，只能得到一定的概率分布。

这就要求我们在实验设计和数据分析中考虑到不确定性的存在。

例如，在测量粒子的位置时，我们需要使用一定的测量精度来描述位置的不确定度。

作者： 赵裕国
出版物刊名： 湖北科技学院学报
页码： 43-46页
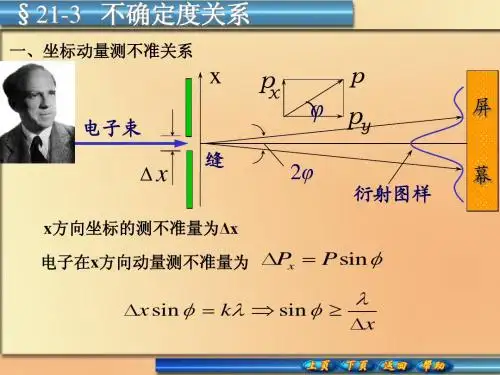
主题词： 测不准原理;海森堡;量子效应;弹簧振子;统计规律;经典物理;经典力学;单缝衍射;普朗克常数;正方向
摘要：<正> 1927年海森堡提出了量子力学中的一个重要原理——测不准关系。

在这之后七十多年的时间里,对测不准关系的理解,一直存在着分歧。

现在较为普遍的观点认为,连提出这个原理的海轰堡自己,对它的理解也是错误的。

本文想通过对如下两个问题的讨论,来谈谈自己对测不准关系的理解。