气体性质计算题简编 含答案

气体的性质1.如下图所示，一气缸内充满1标准大气压的空气，缸内有一个空心的铁球，其质量m =10克，半径为2厘米，此时缸内的温度是0℃，气缸顶上有一面积S＝100厘米2的重力可以忽略的活塞，活塞可以无摩擦地上下自由移动，为了使铁球离开缸底，在活塞上至少要加多大的外力?(大气压强P o＝10牛/厘米2，空气的摩尔质量M＝29克/摩尔)2.如下图所示，一根一端封闭的玻璃管，长为l=96厘米，内有一段长为h=20厘米的水银柱，当温度为27℃时，开口端竖直向上，被封闭气体长度为H=60厘米，问温度至少升至多高时，水银才能从管中全部溢出(大气压P o＝76厘米汞柱)?3.如下图所示，水平固定的圆筒由足够长的粗筒和细筒相接而成，筒中有直径不同的两个活塞A、B，用一根细绳相线，活塞B通过水平细绳，定滑轮与一质量为2.0kg的重物C连接，A、B两活塞的横截面积分别为20cm2和10cm2。

当两活塞封闭的空气柱温度为327℃时，两活塞保持静止，此时两活塞分别与大小圆筒的相接面的距离均为l。

已知大气压强为1 .0×105P a，活塞与筒壁，滑轮与轮轴间的摩擦均可忽略不计，取g=10m/s2求：(1)此时筒内两活塞间气柱的压强多大?(2)当筒内气体的温度缓慢降至27℃时，活塞A能否向右移距离l?试说明理由。

(3)当气柱温度降至27℃时，筒内气体的压强为多大?(在整个变化过程中，A、B间绳子始终有张力)4.如右图所示，长为2l的圆筒形气缸可沿动摩擦因数为 的水平面滑动，在气缸中央有一截面积为S的活塞，气缸内气体的温度为T o，压强为P o(大气压也为P o)，在墙壁与活塞之间装有劲度系数为K的弹簧，当活塞处于图中所示位置时，弹簧恰在原长位置，今使气缸内气体体积增加1倍，问气体的温度应达多少?(气缸内壁光滑，活塞和气缸总质量为m)。

5．一根内径均匀，一端封闭，另一端开口的直玻璃管，长l=100cm，用一段长h=25cm的水银柱将一部分空气封在管内，将其开口朝上竖直放置，被封住的气柱长l0=62.5cm。

一、填空题1．温度为400K ，体积为2m 3的容器中装有2mol 的理想气体A 和8mol 的理想气体B ，则该混合气体中B 的分压力p B =（ ）KPa 。

13.3022．在300K ，100KPa 下，某理想气体的密度ρ=80.8275×10-3kg ·m -3。

则该气体的摩尔质量M=（ ）。

3．恒温100°C 下，在一带有活塞的气缸中装有3.5mol 的水蒸气H 2O （g ），当缓慢地压缩到压力p=（ ）KPa 是才可能有水滴H 2O （l ）出现。

4．恒温下的理想气体，其摩尔体积随压力的变化率Tmp V ⎪⎪⎭⎫ ⎝⎛∂∂ =（ ）。

5，一定的范德华气体，在恒容条件下，其压力随温度的变化率()=∂∂V T /p .6．理想气体的微观特征是：（ ）7. 在临界状态下，任何真实气体的宏观特征为：（ ）8. 在n,T 在一定的条件下，任何种类的气体当压力趋近于零时均满足：()=→pV p lim 0（ ）.9.实际气体的压缩因子定义为Z=（ ）。

当实际气体的Z>1时，说明该气体比理想气体（ ）三、问答题理想气体模型的基本假设是什么？什么情况下真实气体和理想气体性质接近？增加压力真实气体就可以液化，这种说法对吗，为什么？第二章 热力学第一定律――附答案一、填空题1. 理想气体向真空膨胀过程 , 下列变量中等于零的有 : 。

2. 双原子理想气体经加热内能变化为 ，则其焓变为 。

3. 在以绝热箱中置一绝热隔板，将向分成两部分，分别装有温度，压力都不同的两种气体，将隔板抽走室气体混合，若以气体为系统，则此过程 。

4. 绝热刚壁容器内发生CH 4+2O 2=CO 2+2H 2O 的燃烧反应,系统的 Q ___ 0 ; W ___ 0 ;∆U ___ 0;∆H ___ 05. 某循环过程 Q = 5 kJ, 则 ∆U + 2W + 3 ∆(pV) = __________.6. 298K 时, S 的标准燃烧焓为－296.8 kJ ⋅mol －1, 298K 时反应的标准摩尔反应焓 ∆r H m = ________ kJ ⋅mol －1 .7. 已知 的 , 则 的 。

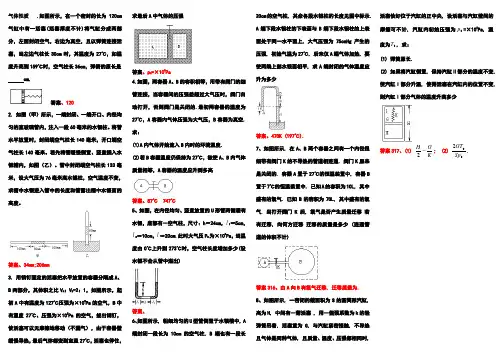
气体性质 .如图所示，在一个密封的长为120cm 气缸中有一活塞(活塞厚度不计)将气缸分成两部分，左面封闭空气，右边为真空，且以弹簧连接活塞，当左边气柱长30cm时，其温度为27℃，如温度升高到159℃时，空气柱长36cm，弹簧的原长是 cm.答案、1202. 如图（甲）所示，一端封闭、一端开口、内径均匀的直玻璃管内，注入一段60毫米的水银柱。

将管水平放置时，封闭端空气柱长140毫米，开口端空气柱长140毫米。

若先将管缓慢倒置、竖直插入水银糟内，如图（乙）。

管中封闭端空气柱长133毫米，设大气压为76毫米高水银柱，空气温度不变，求槽中水银进入管中的长度和管露出槽中水银面的高度。

答案、34mm;206mm3. 用销钉固定的活塞把水平放置的容器分隔成A、B两部分，其体积之比V A：V B=2：1，如图所示，起初A中有温度为127℃压强为×105Pa的空气，B中有温度27℃、压强为×105Pa的空气，拔出销钉，使活塞可以无摩擦地移动（不漏气），由于容器壁缓慢导热，最后气体都变到室温27℃，活塞也停住，求最后A中气体的压强答案、p A=×105Pa4.如图，两容器A、B的容积相等，用带有阀门的细管连接，当容器间的压强差超过大气压时，阀门自动打开，否则阀门是关闭的.最初两容器的温度为27℃，A容器内气体压强为大气压，B容器为真空.求：(1)A内气体开始流入B内时的环境温度.(2)若B容器温度仍保持为27℃，欲使A、B内气体质量相等，A容器的温度应升到多高答案、87℃ 747℃5、如图，在内径均匀、竖直放置的U形管两侧灌有水银，底部有一空气柱，尺寸：h＝24cm，l1＝5cm，l2＝10cm，l＝20cm.此时大气压P0为×105Pa，当温度由0℃上升到273℃时，空气柱长度增加多少(设水银不会从管中溢出)答案、6、如图所示, 粗细均匀的U型管倒置于水银槽中, A端封闭一段长为10cm的空气柱, B端也有一段长20cm的空气柱, 其余各段水银柱的长度见图中标示.A端下段水银柱的下表面与B端下段水银柱的上表面处于同一水平面上, 大气压强为75cmHg产生的压强, 初始气温为27℃, 后来仅A端气体加热, 要使两端上部水银面相平, 求A端封闭的气体温度应升为多少答案、470K (197℃).7、如图所示, 在A、B两个容器之间有一个内径很细带有阀门K的不导热的管道相连通. 阀门K原来是关闭的. 容器A置于27℃的恒温装置中, 容器B置于7℃的恒温装置中. 已知A的容积为10L, 其中盛有的氧气. 已知B的容积为70L, 其中盛有的氧气. 当打开阀门K后, 氧气是否产生质量迁移若有迁移, 向何方迁移迁移的质量是多少 (连通管道的体积不计)答案316、由A向B有氧气迁移, 迁移质量为.8、如图所示, 一密闭的截面积为S的圆筒形汽缸,高为H, 中间有一薄活塞 , 用一倔强系数为k的轻弹簧吊着, 活塞重为G, 与汽缸紧密接触, 不导热且气体是同种气体, 且质量、温度、压强都相同时,活塞恰好位于汽缸的正中央, 设活塞与汽缸壁间的摩擦可不计, 汽缸内初始压强为p=×105Pa, 温度为T, 求：(1) 弹簧原长.(2) 如果将汽缸倒置, 保持汽缸Ⅱ部分的温度不变,使汽缸Ⅰ部分升温, 使得活塞在汽缸内的位置不变,则汽缸Ⅰ部分气体的温度升高多少答案317、(1)KGH2; (2)2SpGT.气体性质 . 如图所示，在一个密封的长为120cm气缸中有一活塞(活塞厚度不计)将气缸分成两部分，左面封闭空气，右边为真空，且以弹簧连接活塞，当左边气柱长30cm时，其温度为27℃，如温度升高到159℃时，空气柱长36cm，弹簧的原长是cm.2. 如图（甲）所示，一端封闭、一端开口、内径均匀的直玻璃管内，注入一段60毫米的水银柱。

气体的PVT性质习题一、简答题1、物质的聚集状态分为哪三种，用符号怎么表示？2、名词解释：气体的压强、体积、温度3、理想气体存在吗？真实气体的pVT行为在何种条件下可用pV=nRT来描述？4、理想气体的微观模型是什么?5、分压和分体积定律只适用于理想气体混合物吗？能否适用于真实气体？6、范德华方程式是根据哪两个因素来修正理想气体状态方程的？7、实际气体与理想气体的差异是什么？8、不同气体的压缩因子z值在定温下随压力P是如何变化的？二、计算题1、混合气体中各组分的物质的量分数分别为：氯乙烯0.72、氯化氢0.10和乙烯0.18。

在保持压力101.325kPa不变的条件下，用水洗去氯化氢枯燥，求剩余干气体中各组分的分压力。

2、30℃时，在一个10.0L的容器中，O2，N2和CO2混合物的总压为93.3kPa。

分析结果得p(O2)=26.7kPa,CO2的含量为5.00g，求容器中：a. p(CO2)；b.p(N2)；c.O2的摩尔分数。

3、 10.0 mol C2H6气体在300K充入4.86×10－3m3的容器中，测得其压力为3.445 MPa。

分别用〔1〕理气状态方程〔2〕范德华方程计算容器内气体的压力〔a=0.5562 Pa·m3/mol2;b=6.380×10－3 m3/mol〕。

气体的PVT性质习题参考答案一、简答题1、物质的聚集状态分为哪三种，用符号怎么表示？答：物质的聚集状态分为气体、液体和固体，分别用符号g，l，s表示。

2、名词解释：气体的压强、体积、温度答：由于分子的热运动，气体分子不断地与容器壁碰撞，对器壁产生作用力。

单位面积器壁上所受的力称为压强，用符号p表示，法定计量单位是Pa(帕斯卡)。

气体的体积即它们所占空间的大小，用符号V 表示。

由于气体能充满整个容器，所以气体的体积就是气体容器的容积，单位是m3(立方米)。

气体的温度是定量反映气体冷热程度的物理量。

物理化学气体性质习题答案物理化学气体性质习题答案气体是物理化学中一个重要的研究对象，其性质和行为对于我们理解自然界和应用科学原理具有重要意义。

在学习物理化学的过程中，我们经常会遇到一些关于气体性质的习题。

下面，我将为大家提供一些常见气体性质习题的答案，希望能对大家的学习有所帮助。

1. 问题：一定体积的气体在恒定温度下，压强与摩尔数成正比。

如果将气体的摩尔数增加一倍，压强会发生什么变化？答案：根据查理定律，一定体积的气体在恒定温度下，压强与摩尔数成正比。

因此，当气体的摩尔数增加一倍时，压强也会增加一倍。

2. 问题：一定质量的气体在恒定温度下，体积与压强成反比。

如果将气体的压强减小一半，体积会发生什么变化？答案：根据波义耳定律，一定质量的气体在恒定温度下，体积与压强成反比。

因此，当气体的压强减小一半时，体积会增加两倍。

3. 问题：一定质量的气体在恒定温度下，体积与摩尔数成正比。

如果将气体的摩尔数减少一半，体积会发生什么变化？答案：一定质量的气体在恒定温度下，体积与摩尔数成正比。

因此，当气体的摩尔数减少一半时，体积也会减少一半。

4. 问题：一定质量的气体在恒定温度下，压强与体积成正比。

如果将气体的体积增加一倍，压强会发生什么变化？答案：根据阿伏伽德罗定律，一定质量的气体在恒定温度下，压强与体积成正比。

因此，当气体的体积增加一倍时，压强也会减少一倍。

5. 问题：一定质量的气体在恒定温度下，压强与摩尔数成正比。

如果将气体的摩尔数减少一半，压强会发生什么变化？答案：一定质量的气体在恒定温度下，压强与摩尔数成正比。

因此，当气体的摩尔数减少一半时，压强也会减少一半。

以上是一些常见的物理化学气体性质习题的答案。

通过解答这些习题，我们可以更好地理解气体的性质和行为。

当然，除了这些基本的性质关系，气体还有很多其他的性质和行为，例如气体的扩散性、气体的溶解度等等。

希望大家在学习和应用物理化学的过程中，能够深入理解气体的性质，掌握相关的理论知识，并能够灵活运用于实际问题的解决中。

化学气体的理想气体定律练习题及解答化学气体的理想气体定律练习题及解答1. 问题一：理想气体定律的表达式是什么？请简要说明每个符号的含义。

理想气体定律的表达式为PV = nRT，其中：- P代表气体的压强（单位为帕斯卡）- V代表气体的体积（单位为立方米）- n代表气体的物质的量（单位为摩尔）- R代表气体常数（单位为焦耳·摩尔^-1·开尔文^-1）- T代表气体的温度（单位为开尔文）2. 问题二：根据理想气体定律回答以下问题：a) 一个由1摩尔氧气组成的气体在温度为300K下，占据1升的体积，求气体的压强。

根据理想气体定律，我们有PV = nRT。

将已知值代入计算得到：P = (1 mol)(8.314 J·mol^-1·K^-1)(300 K)/(1 L) = 24.942 J·L^-1·mol^-1因此，气体的压强为24.942 J·L^-1·mol^-1。

b) 一气缸中装有4摩尔氢气，并且体积为5升。

如果气缸的温度是350K，求气体的压强。

同样地，根据理想气体定律，我们有PV = nRT。

将已知值代入计算得到：P = (4 mol)(8.314 J·mol^-1·K^-1)(350 K)/(5 L) = 233.392 J·L^-1·mol^-1因此，气体的压强为233.392 J·L^-1·mol^-1。

c) 一气缸中装有2摩尔二氧化碳气体，并且温度为400K。

如果气体的压强为80 J·L^-1·mol^-1，求气体的体积。

根据理想气体定律，我们有PV = nRT。

将已知值代入计算得到：V = (2 mol)(8.314 J·mol^-1·K^-1)(400 K)/(80 J·L^-1·mol^-1) = 41.57 L 因此，气体的体积为41.57升。

气体性质计算题简编含答案SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#3-3气体性质计算题简编1.如图所示，活塞把密闭气缸分成左、右两个气室，每室各与U 形管压强计的一臂相连，压强计的两壁截面处处相同，U 形管内盛有密度为32/105.7m kg ⨯=ρ的液体。

开始时左、右两气室的体积都为320102.1M V -⨯=，气压都Pa p 30100.4⨯=，且液体的液面处在同一高度，如图19－2所示，现缓慢向左推进活塞，直到液体在U 形管中的高度差h=40cm ，求此时左、右气室的体积1V 、2V ，假定两气室的温度保持不变，计算时可以不计U 形管和连接管道中气体的体积，g 取2/10s m 。

2.某房间的容积为20m 3，在温度为17℃，大气压强为74 cm Hg 时，室内空气质量为25kg ，则当温度升高到27℃，大气压强变为76 cm Hg 时，室内空气的质量为多少千克3.向汽车轮胎充气，已知轮胎内原有空气的压强为个大气压，温度为20℃，体积为20L ，充气后，轮胎内空气压强增大为个大气压，温度升为25℃，若充入的空气温度为20℃，压强为1个大气压，则需充入多少升这样的空气(设轮胎体积不变)．4.如图13－60所示，气缸A 和容器B 由一细管经阀门K 相连，A 和B 的壁都是透热的，A 放在27℃、1标准大气压的大气中，B 浸在127℃的恒温槽内，开始时K 是关断的，B 内没有气体，容积V B ＝2.4L ，A 内装有气体，体积V A ＝4.8L ，打开K ，使气体由A 流入B ，等到活塞D 停止移动时，A 内气体体积是多大假设活塞D 与气缸壁之间没有摩擦，细管的容积忽略不计．5.如下图所示，粗细均匀的U 形玻璃管竖直放置，两臂长为50cm.在两管中注入10cm 高的水银后，封闭左管口，求继续向右管中注入多高的水银，可使左管水银面上升4cm ，设整个过程中温度保持不变，且大气压强P 0＝760mmHg.6.如下图所示，活塞A 将一定质量的气体封闭在汽缸B 内，当汽缸竖直放置时，活塞到缸底的距离为60cm ，活塞与汽缸间摩擦不计，大气压强为×105Pa.现将汽缸平放在水平地面上，测得活塞A 到缸底的距离为100cm ，并测得汽缸B 的截面积S ＝100cm 2，求活塞A 的质量.7.如下图所示中一个横截面积为10cm 2的容器内，有一个用弹簧和底面相连的活塞，当温度为27℃，内外压强都是×105Pa 时，活塞和底面相距10cm ，在活塞上放质量为40kg 的物体，活塞下降5cm ，温度仍为27℃(活塞质量不计，g 取9.8m/s 2)，求：(1)弹簧劲度系数k;(2)如把活塞内气体加热到57℃，为保持活塞位置仍下降5cm ，活塞上应再加的物体质量为多少8.如下图所示，气缸内底部面积为0.02米2，被活塞封闭在气缸内的空气温度为-5℃，活塞质量为8千克，当气缸缸筒与水平面成60°角时，活塞距缸底L ，现将气缸直立，如图所示.欲使活塞距缸底仍为L ，应使缸内气体升高到多少摄氏度(大气压强p 0＝×105帕，g ＝10m/s 2)9.如图所示，水平放置的密封气缸的活塞被很细的弹簧拉住，气缸内密封一定质量的气体.当缸内气体温度为27℃，弹簧的长度为30cm 时，气缸内气体压强为缸外大气压的倍.当缸内气体温度升高到127℃时，弹簧的长度为36cm.求弹簧的原长(不计活塞与缸壁的摩擦)10.如下图所示，一圆柱形气缸直立在水平地面上，内有质量不计的可上下移动的活塞，在距缸底高为2H 0的缸口处有固定的卡环；使活塞不会从气缸中顶出，气缸壁和活塞都是不导热的，它们之间没有摩擦.活塞下方距缸底高为H 0处还有一固定的可导热的隔板，将容器分为A 、B 两部分，A 、B 中各封闭同种的理想气体，开始时A 、B 中气体的温度均为27℃，压强等于外界大气压强P 0，活塞距气缸底的高度为，现通过B 中的电热丝缓慢加热，试求：(1)当B 中气体的压强为时，活塞距缸底的高度是多少 (2)当A 中气体的压强为时，B 中气体的温度是多少11.如图所示，内径均匀的U 型细玻璃管一端开口，竖直放置，开口端与一个容积很大的贮气缸B 连通，封闭端由水银封闭一段空气A ，已知-23℃时空气柱A 长62cm ，右管水银面比左管水银面低40cm ，当气温上升到27℃时，水银面高度差变化4cm ，B 贮气缸左侧连接的细管的体积变化不计.(1)试论证当气温上升到27℃时，水银面高度差是增大4cm 还是减小4cn (2)求-23℃时贮气缸B 中气体的压强.参考答案1.解 以1p 、1V 表示压缩后左室气体的压强和体积，2p 、2V 表示这时右室气体的压强和体积，0p 、0V 表示初态两室气体的压强和体积。

气体的性质1.如下图所示，有一个圆筒形容器，长为3L ，其中装有两个可移动的活塞，分别把两部分气体封闭在圆筒的两部分A 和B 中，A 和B 中为等质量的同种气体，两活塞之间有一被压缩的弹簧且为真空，其自然长为2L ，劲度系数为K ，当AB 两部分气温为T 1开时，弹簧的长为L ，整个系统保持平衡。

现使气温都下降为T 2开，弹簧的长度变为1.5L ，则12T T ＝ 。

1.3/82.如下图所示为0.2摩尔的某种气体的压强与温度的关系，图中P 0为标准大气压， 气体在B 状态时的体积是 。

2.5.6升3.使一定质量的理想气体如下图中箭头所示的顺序变化，图线BC 是一段以纵轴和横轴为渐近线的双曲线，已知气体在状态A 的温度T A ＝300K ，则气体在状态B 、C 和D 的温度 T B ＝ ，T C ＝ ，T D ＝ 。

3.T B ＝T C ＝600k ；T D ＝300k4.在圆形容器内有一弹簧，上端固定，下端连一重力不计的活塞，活塞与容器内壁 之间不漏气且不计摩擦，容器内活塞上面部分为真空，当弹簧自然伸长时，活塞刚好能触及到容器底部，如果活塞下面充入一定质量的温度为T的某种气体，使活塞下面气柱的高度为h ，如右图所示，当容器内气体温度升高到T 1时，则气柱的高度h 1= 。

4. T T h /15.用注射器验证玻—马定律实验中，因活塞不便从注射器上拆下，为了知道活塞压 气体时产生的附加压强ΔP ，一位学生采用了这样的方法：先使注射器如图(a)竖直放置，读出封闭气体体积V 1＝36毫升，然后把注射器倒转180°，如下图(b)放置，读出封闭气体体积 V 2＝38毫升，已知大气压为P o ＝76厘米汞柱，则由活塞重力对气体产生的附加压强为 。

5.2.05cmHg6.潜水艇的贮气筒与水箱相连，当贮存的空气压入水箱后，水箱就排出水使潜水艇 浮起。

某潜水艇贮气筒的容积为2米3，贮有压强为2.00×107帕的压缩气体。

气体性质推断题汇总及答案
题目1：
一瓶氧气和一瓶氮气，它们外形一样，重量一样，在正常大气压下，它们吸收热量的多少一样吗？
答案：一样。

因为它们在相同的温度下，吸收的热量由内能决定，与它们的化学成分和分子大小无关。

题目2：
同一质量的同种气体在相等的体积和温度下混合时，混合气的分压强度增大了吗？
答案：不一定，与两种气体的分子之间作用有关。

如果气体A 和气体B之间相互作用力小于气体A内分子间作用力和气体B内分子间作用力，则以该温度下，气体A与气体B混合的分压强度之和小于两者分别各自的分压强度之和；如果相互作用力大于两气体内部的作用力，则混合气的分压强度之和大于各自的分压强度之和。

题目3：
在常压下，1L氧气（O2）在25℃下可以溶解0.04克，而1L
二氧化碳（CO2）在25℃下只能溶解0.02克，暗示氧气比二氧化
碳
A.分子量大
B.游离能低
C.化学活性强
D.分子之间缔合力小
答案：D。

氧气分子之间缔合力弱，容易吸附在水等介质的表面，而二氧化碳分子之间缔合力较强，容易形成络合物而难以溶解。

题目4：
一个二つ相等、内装气体的温度计，它的校准是在1大气压下的，如果该温度计被带到了2000米高度，此时读数偏向哪里了？
答案：读数偏低。

因为气压减小，导致液柱下降，读数偏低。