5.2视图(一)教学设计

教师学科教案[ 20 – 20 学年度第__学期]任教学科：_____________任教年级：_____________任教老师：_____________xx市实验学校第五章投影与视图2.视图（一）一、学生起点分析学生的知识技能基础：学生在七年级已经学习过从三个方向观察物体的形状，并画出形状图。

学生的活动经验基础：在相关知识的学习过程中，学生已经经历了判断一个几何体从不同方向看得到的形状图，解决了一些生活中简单的现实问题，感受到了数学和现实生活的密切联系，获得了数学来源于生活的切身感受和体验；同时在以前的数学学习中学生已经经历了很多合作学习的过程，具有了一定的合作学习的经验，具备了一定的合作与交流的能力。

二、教学任务分析本章第一节学习了投影知识，然后将正投影称为物体的视图，进而提出本节课具体的学习任务：理解三视图的具体特点和他们之间的相互联系，并能根据不同问题选择适当的方法解决问题。

但这仅仅是这节课具体的教学目标，或者说是一个近期目标。

数学教学由一系列相互联系而又渐次递进的课堂组成，因而具体的课堂教学也应满足于整个数学教学的远期目标，或者说，数学教学的远期目标，应该与具体的课堂教学任务产生实质性联系。

同时也应力图在学习中逐步达成学生的有关情感态度目标。

为此，本节课的教学目标是：①经历由实物抽象出几何体的过程，进一步发展空间观念；②探索基本几何体（圆柱、圆锥、球）与其三种视图（主视图、左视图、俯视图）之间的关系；③会判断简单物体的三视图，发展合情推理能力和数学表达能力；④结合具体实例，初步体会视图在现实生活中的应用，感受数学与现实生活的密切联系，增强学生的数学应用意识。

三、教学过程分析本节课共分三个课时，第一课时主要是探索基本几何体（圆柱、圆锥、球）与其三种视图（主视图、左视图、俯视图）之间的关系，会判断简单物体的三视图；第二课时主要研究棱柱的三种视图；第三课时根据三种视图描述基本几何体或实物原型。

作业要求：
1.作业须在课后独立完成，要求字迹清晰，绘图规范，标注准确。
2.必做题须全部完成，选做题可根据个人兴趣和能力选择一题完成。
3.探究题要求小组合作，共同完成，并在下节课上进行分享和交流。
作业提交时间：
1.必做题和选做题请在下次课前提交。
2.探究题在下节课上进行分享，同时提交书面报告。
作业评价：
c.对学生绘制的三视图进行评价和反馈，纠正错误，提高绘制技能。
3.运用信息技术手段，如计算机软件、网络资源等，辅助教学。例如，使用三维建模软件展示物体的三视图，让学生更直观地理解视图之间的关系。
4.创设合作学习氛围，鼓励学生之间相互交流、讨论，共同解决问题。教师在此过程中，要关注学生的讨论，适时给予指导和启发，提高学生的空间想象能力和逻辑思维能力。
a.观察生活中的一些建筑物或家居用品，尝试用视图的方式表达出来，并简要说明其特点。
b.搜集一些工程图纸，分析其三视图，了解视图在实际工程中的应用。
3.探究题：
a.以小组为单位，讨论并总结三视图之间的相互关系及其在空间想象中的作用。
b.每个小组选择一个物体，通过实际测量和绘制，验证三视图与实际物体之间的对应关系。
7.注重课后辅导和拓展，针对学生在课堂上遇到的困难和问题，进行个性化辅导。同时，鼓励学生参加课外活动，如科技竞赛、实践活动等，提高学生的实际操作能力和综合素质。
四、教学内容与过程
（一）导入新课
1.利用生活实例引发学生兴趣：在课堂开始时，展示一些生活中常见的物体，如教呢？”通过这个问题，引发学生对视图知识的好奇心。
1.教师将对作业进行全批全改，关注学生的知识掌握程度和实际应用能力。
2.对学生的作业给予及时反馈，鼓励学生发挥潜能，提高空间想象能力。

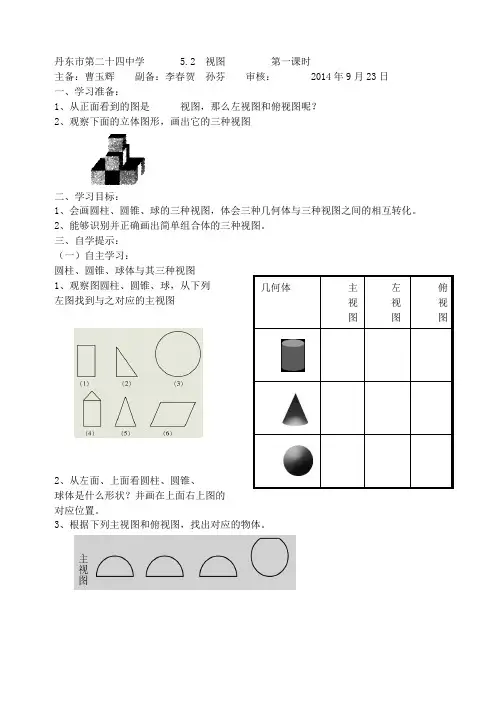
丹东市第二十四中学 5.2 视图 第一课时
主备：曹玉辉 副备：李春贺 孙芬 审核： 2014年9月23日 一、学习准备：
1、从正面看到的图是 视图，那么左视图和俯视图呢？
2、观察下面的立体图形，画出它的三种视图
二、学习目标：
1、会画圆柱、圆锥、球的三种视图，体会三种几何体与三种视图之间的相互转化。

2、能够识别并正确画出简单组合体的三种视图。

三、自学提示： （一）自主学习：
圆柱、圆锥、球体与其三种视图 1、观察图圆柱、圆锥、球，从下列 左图找到与之对应的主视图
2、从左面、上面看圆柱、圆锥、
球体是什么形状？并画在上面右上图的 对应位置。

3、根据下列主视图和俯视图，找出对应的物体。

（二）合作探究：
下图是一个类似蒙古包的几何体，在其右方画出这个几何体的三种视图。

四、学习小结：
五、夯实基础：
1．一个物体的俯视图是圆，则该物体可能是：（）
A．球体 B．圆柱 C．圆锥 D．以上都有可能
2．某物体的三种视图是如图所示的3个图形，那么该物体的形状是（）
A．长方体 B．圆锥体 C．立方体 D．圆柱体
3. 一个立体图形的三视图完全相同，则这个立体图形可能是 ( )
A．球或圆锥 B．正方体或圆柱C．球或正方体 D．以上都不对
六、能力提升：
如图是由若干个同样大小的立方体搭成的几何体的俯视图，小正方形中的数字表示该位置立方体的个数，则这个几何体的主视图是 (
布置作业：。

上述物体的形状分别可以看成圆柱、圆 锥和球。它们的三种视图如下表所示：
几何体 主视图 左视图 俯视图
主视图
左视图
俯视图
※随堂练习:
1、找出图中每 一物品所对应 的主视图：
2、将两个圆盘、一个茶叶、一个皮球和一个蒙古 包如图的方式摆放在一起，其主视图是（ D ）
名 茶
3、画出图中各物体的主视图、左视图和俯视图：
中学生导报提供
教学目标
1．经历由实物抽象出几何体的过程，进一步 发展空间观念. 2．会画圆柱、圆锥、球及其组合体的三种视 图，体会这几种几何体与其视图之间的相 互转化. 3. 结合具体实例，初步体会视图在现实生活 中的应用，感受数学与现实生活的密切联 系，增强学生的数学应用意识.
问题：我们前面学习了
第一幅
第三幅
第二幅
4、根据下列主视图和俯视图，找出对应的物 体。
主 视 图 俯 视 图
1
2
3
4
交流小结，收获感悟
1. 对自己说，你有什么收获？ 2. 对同学说，你有什么温馨提示？
3. 对老师说，你还有什么困惑？
布置作业，用正投影的方法绘制的物体在投影面 上的图形，称为物体的视图.
三视图的概念： 通常我们把从正面得到的视图，称为主视图； 从上面得到的视图，称为俯视图； 从左面得到的视图，称为侧视图.
请你画出三个视图：
※议一议 下面各图中物体形状分别可以看成什么样的几何体?
圆柱
圆锥
球
从正面,侧面,上面看这些几何体,它们的形状各是什 么样的? 正面看:长方形 等腰三角形 圆 侧面看:长方形 等腰三角形 圆 上面看: 圆 圆 能画出各物体的三视图吗? 圆
投影，那么什么叫投影，

北师大版九年级数学上册《第五章投影与视图 5.2 视图》一. 教材分析北师大版九年级数学上册《第五章投影与视图 5.2 视图》这一节主要让学生了解三视图的概念，学会如何从不同角度观察物体，并能够正确地画出物体的三视图。

教材通过丰富的图片和实例，引导学生探究和发现物体的不同视图，从而培养学生的空间想象能力和抽象思维能力。

二. 学情分析九年级的学生已经具备了一定的空间想象能力和抽象思维能力，他们对平面几何图形有较深入的了解。

但是，对于从不同角度观察物体，并画出其三视图，可能还存在一定的困难。

因此，在教学过程中，教师需要利用学生已有的知识基础，通过引导和探究，帮助他们理解和掌握三视图的概念。

三. 教学目标1.了解三视图的概念，知道主视图、左视图、俯视图的特点。

2.学会从不同角度观察物体，并能够正确地画出物体的三视图。

3.培养学生的空间想象能力和抽象思维能力。

四. 教学重难点1.重点：三视图的概念，主视图、左视图、俯视图的特点。

2.难点：如何从不同角度观察物体，并能够正确地画出其三视图。

五. 教学方法采用问题驱动法、合作交流法和实例分析法进行教学。

通过提出问题，引导学生思考和探究；通过合作交流，让学生分享和讨论自己的观点；通过实例分析，让学生直观地了解和掌握三视图的概念。

六. 教学准备1.准备一些实物模型，如立方体、圆柱体等。

2.准备多媒体教学课件，包括图片、实例和动画等。

七. 教学过程1.导入（5分钟）通过展示一些实物模型，如立方体、圆柱体等，让学生观察并思考：从不同的角度观察这些物体，你都能看到哪些图形？引导学生发现，从不同的角度观察物体，所能看到的图形是不同的。

2.呈现（10分钟）利用多媒体教学课件，呈现一些实例，让学生观察并回答问题：这些物体的三视图分别是什么？主视图、左视图、俯视图有什么特点？通过实例分析，让学生了解和掌握三视图的概念。

3.操练（10分钟）让学生分组合作，选取一些物体，尝试画出它们的三视图。

其次，我发现学生们在绘制圆柱和圆锥的视图时存在一定难度。这说明这些部分是教学的难点，我需要在今后的课程中加强对此类问题的讲解和练习，以便帮助学生更好地掌握。
此外，小组讨论环节让学生们充分参与到了课堂中，他们积极发表观点，交流想法，这有助于提高他们的合作能力和沟通能力。在今后的教学中，我会继续采用这种形式，鼓励学生们多思考、多讨论，发挥他们的主观能动性。
五、教学反思
在今天这节课中，我们探讨了简单几何体的三种视图，我发现学生们对这一概念表现出很大的兴趣。他们通过观察和动手操作，逐渐理解了正视图、左视图和俯视图之间的关系。在讲授过程中，我注意到几个关键点：
首先，通过引入日常生活中的例子，学生们能够更直观地理解视图的概念，这有助于他们建立起抽象知识与现实世界间的联系。在今后的教学中，我应继续寻找更多贴近生活的实例，让学生感受到数学的实用性和趣味性。
2.教学难点
-空间想象能力的培养：学生需要具备将二维视图与三维几何体相互转换的能力，这对空间想象力有一定要求。
-视图的绘制技巧：学生需要掌握如何将三维几何体准确地转化为二维视图，特别是在处理圆柱和圆锥的视图时，需要注意圆的投影和边缘线的表示。
-实际问题中的应用：学生需要将所学知识应用到实际问题中，如根据视图来估计几何体的尺寸或形状，这对学生的理解和应用能力是一个挑战。
然而，我也注意到，在讨论过程中，部分学生表现较为内向，不太愿意主动参与。为了提高这部分学生的积极性，我会在课后找他们单独交流，了解他们的想法，鼓励他们大胆表达自己。
在实践活动方面，学生们对实验操作表现出很高的热情，但也有一部分学生在操作过程中遇到了困难。针对这一情况，我将在今后的教学中加强对学生的个别指导，确保他们能够顺利完成实验。
4.运用三种视图解决实际问题，培养空间想象力和思维能力。

3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了视图的基本概念、创建方法、应用场景和安全性控制。同时，我们也通过实践活动和小组讨论加深了对视图的理解。我希望大家能够掌握这些知识点，并在数据库设计和查询中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
2.逻辑思维与创新能力：在视图创建和维护过程中，锻炼学生逻辑思维，激发创新意识，使学生能够灵活运用视图解决复杂问题。
3.团队协作与沟通能力：通过小组讨论、分享视图应用案例，促进学生之间的沟通与协作，培养团队精神。
4.信息素养与安全意识：让学生了解视图在信息处理中的重要作用，同时强调视图安全性控制的意义，提高信息安全意识。
-解释：视图的数据来源于查询结果，需要学生理解查询语句的执行过程和结果集的概念。
-视图的更新操作：视图的更新涉及到底层表的变动，学生需要理解这种关联关系，掌握正确的更新方法。
-解释：更新视图时，需要考虑视图中的数据与底层表的关系，避免出现数据不一致的问题。
-视图的安全性控制：如何通过视图实现数据的安全性控制，这是学生理解的难点。
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是“5.2.2视图”这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要从大量数据中提取有用信息的情况？”例如，我们在使用社交媒体时，如何快速查看特定朋友的所有动态？这个问题与我们将要学习的视图密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索视图的奥秘。
在小组讨论环节，学生们表现得积极主动，大家都能参与到讨论中。但在分享成果时，我发现有些学生表达不够清晰，可能是因为对知识点理解不够深入。在以后的教学中，我会鼓励学生们多发言，提高他们的表达能力和自信心。

3.教师巡回指导，及时给予学生反馈，帮助学生解决问题，提高学生的学习效果。
（四）总结归纳
1.引导学生对所学知识进行反思，总结主视图、左视图、俯视图的定义及画法，提高学生的思维能力。
2.组织学生进行自我评价，鼓励他们发现自己的优点和不足，制定改进措施。
3.教师对学生的学习过程和结果进行评价，关注学生的全面发展，为他们的终身发展提供指导。
二、教学目标
（一）知识与技能
1.理解主视图、左视图、俯视图的概念，掌握三种视图的画法及转换。
2.能够从不同角度观察物体，培养空间想象能力，提高几何思维能力。
3.学会用视图的知识解决实际问题，提高解决问题的能力。
（二）过程与方法
1.通过观察实际物体，引导学生发现视图的规律，培养学生的观察能力和发现问题、解决问题的能力。
3.培养学生诚实守信、勇于面对困难的品质，克服学习中遇到的困难，增强自信心。
4.培养学生关爱环境、珍惜资源的意识，通过解决实际问题，为可持续发展贡献力量。
作为一名特级教师，我深知教学目标的重要性，它是课堂教学的灵魂和核心。在教学过程中，我将紧紧围绕教学目标，采用多种教学方法和手段，努力提高课堂教学效果，使学生在知识、能力、情感等方面得到全面发展。同时，关注每一个学生，尊重学生的个性差异，激发学生的潜能，为他们的终身发展奠定坚实基础。
2.鼓励学生发挥自己的特长，为小组作出贡献，培养学生的团队精神和自信心。
3.教师巡回指导，及时给予学生反馈，帮助学生解决问题，提高学生的学习效果。
（四）反思与评价
1.引导学生对所学知识进行反思，总结主视图、左视图、俯视图的定义及画法，提高学生的思维能力。
2.组织学生进行自我评价，鼓励他们发现自己的优点和不足，制定改进措施。

5.2視圖第1課時簡單圖形的三視圖1.理解視圖及三視圖的概念；2.會辨別簡單幾何體的三種視圖，能熟練畫出簡單幾何體的三種視圖；（重點）3.能根據三視圖描述基本幾何體或實物原型.（難點）一、情景導入一個物體從不同的角度觀察，看到的形狀可能是不相同的.觀察一個毛絨玩具，我們從三個不同的角度看，得到三個圖形，如圖所示.你能說出它們是從哪個方向觀察得到的嗎？二、合作探究探究點一：三視圖的識別【類型一】判斷簡單幾何體的三種視圖圖中的四個幾何體中，主視圖、左視圖和俯視圖都相同的幾何體共有（）A.1個B.2個C.3個D.4個解析：圓柱的主視圖、左視圖都是長方形，而俯視圖是圓；圓錐的主視圖、左視圖都是等腰三角形，而俯視圖是帶圓心的圓；球的三種視圖都是圓；正方體的三種視圖都是正方形，故選B.方法總結：常見的幾何體有圓柱、圓錐、球以及直棱柱，豎直放置的圓柱、圓錐的主視圖、左視圖相同，一般的直棱柱的三種視圖是不同的，而球和正方體的三種視圖都是相同的，它們分別是圓和正方形.【類型二】根據實物確定視圖如圖，從不同方向看一只茶壺，你認為是俯視效果圖的是（）解析：俯視圖就是從物體的正上方向下看到的視圖，因而能夠看到茶壺的頂部、壺把、壺嘴，從而選擇A；D選項是茶壺的主視圖.故選A.方法總結：根據實物確定視圖的方法：首先要弄清楚物體的主視圖、左視圖、俯視圖的含義，而後根據實際物體思考三種視圖的大體輪廓.探究點二：畫簡單幾何體的三種視圖畫出如圖甲所示的幾何體的三種視圖.解析：該幾何體是由圓錐和圓柱組合而成的幾何體，只要把圓錐和圓柱的三種視圖分別畫出再組合即可.解：三種視圖如圖乙所示.方法總結：畫組合體的三種視圖時，先將幾何體分解成若干個簡單幾何體，再進行各種視圖組合.畫圓錐的俯視圖時一定要注意它是一個帶圓心的圓，不要漏畫了圓心.探究點三：根據三視圖還原幾何體【類型一】根據三視圖判斷幾何體的形狀已知一個幾何體的三種視圖如圖所示，則該幾何體是（）解析：A圖的主視圖、左視圖均為等腰三角形，B圖的左視圖、俯視圖均為矩形，C圖的俯視圖的外輪廓線為四邊形，由此可排除A，B，C選項，抓住某個特徵採用排除法是解決這類問題的常用方法.故選D.方法總結：主視圖能體現物體的左右長度、上下高度；俯視圖能體現物體的左右長度、前後寬度；左視圖能體現物體的上下高度、前後寬度.通過觀察三種視圖可以想像出幾何體的立體圖形.【類型二】根據兩種視圖討論構成幾何體的小正方體的個數用小立方體搭一個幾何體，使它的主視圖和俯視圖如圖所示，俯視圖中小正方形中的字母表示在該位置小正方體的個數，請解答下列問題：（1）a，b，c各表示多少？（2）這個幾何體最少由幾個小立方體組成，最多又是多少？（3）當d＝e＝1，f＝2時，畫出這個幾何體的左視圖.解：（1）由俯視圖知道這個幾何體共有三排三列，第三列只有一排，第二列有兩排；而從主視圖知道第三列的層數為3層，第二列的層數為1層，所以a 為3，b，c應為1；（2）d ，e ，f 既可以為1，也可以為2，但至少有一個為2，另外兩個為1時，共有9個小立方體；另外兩個都為2時，共有11個小正方體；故最少由9個小立方體搭成，最多由11個小立方體搭成；（3）左視圖如右圖所示.方法點撥：這類問題一般是給出一個由相同的小正方體搭成的立體圖形的兩種視圖，要求想像出這個幾何體可能的形狀.解答時可以先由三種視圖描述出對應的該物體，再由此得出組成該物體的部分個體的個數.三、板書設計視圖⎩⎪⎪⎨⎪⎪⎧概念：用正投影的方法绘制的物体在投影面上的图形三视图的组成⎩⎪⎨⎪⎧主视图：从正面得到的视图左视图：从左面得到的视图俯视图：从上面得到的视图三视图的画法：长对正，高平齐，宽相等由三视图推断原几何体的形状通過觀察、操作、猜想、討論、合作等活動，使學生體會到三視圖中位置及各部分之間大小的對應關係.通過具體活動，積累學生的觀察、想像物體投影的經驗，發展學生的動手實踐能力、數學思考能力和空間觀念.。

1.学生对视图概念的理解程度：通过课前测试，了解学生对主视图、左视图、俯视图的理解程度，以便在教学中有的放矢地进行针对性讲解。
2.学生的空间想象力：观察学生在课堂上的表现，了解他们在观察和想象物体形状时的困难，以便及时给予指导和帮助。
3.学生的合作与交流能力：在小组合作环节，关注学生的参与程度，鼓励他们积极发表观点，提高团队协作能力和表达能力。
二、新课讲解
1.讲解主视图、左视图、俯视图的概念，强调它们之间的相互关系。
2.通过实例演示，让学生观察和思考如何从不同角度观察物体，并绘制出相应的视图。
3.分析视图在工程设计、建筑、制造等领域的应用，让学生认识到视图知识的重要性。
三、课堂练习
1.让学生独立完成教材中的练习题，巩固所学知识。
2.引导学生运用视图知识解决实际问题，如根据视图设计物体、计算物体的表面积和体积等。
（二）过程与方法
1.通过观察、操作、实践等教学活动，让学生体验从不同角度观察物体，培养空间想象力和观察力。
2.引导学生运用类比、归纳、推理等方法，发现视图之间的内在联系，提高逻辑思维能力和解决问题的能力。
3.通过小组合作、交流讨论等形式，培养学生的团队协作能力和表达能力。
（三）情感态度与价值观
1.培养学生对视图学习的兴趣，激发学生的学习热情，使学生在轻松愉快的氛围中学习数学。
3.教师布置课后作业，要求学生运用所学知识解决实际问题，如根据视图设计物体、计算物体的表面积和体积等。
4.教师提醒学生关注生活中的视图现象，培养学生的观察力和空间想象力，为下一节课的学习打下基础。
五、作业布置
为了巩固本节课所学知识，培养学生的空间想象力和解决问题的能力，特布置以下作业：
1.完成教材课后练习题：要求学生独立完成，注意在绘制视图时保持准确性和规范性。通过完成练习题，使学生进一步熟悉三视图的绘制方法和技巧。

6.鼓励学生利用课余时间，查找有关视图在实际工程、设计等领域应用的案例，拓宽知识视野，提高学生的学习兴趣。
作业布置要求：
1.学生在完成作业时，要注意书写规范，保持解答过程的简洁和清晰。
2.作业完成后，要进行自我检查，确保答案的正确性。
3.教师将对作业进行详细批改，给予评价和指导，学生应认真对待反馈意见，及时改正错误。
4.掌握使用计算器、计算机等工具绘制视图的基本方法，提高动手操作能力和实际应用能力。
（二）过程与方法
1.通过观察、思考、讨论等环节，培养学生提出问题、分析问题、解决问题的能力。
2.通过小组合作、互动交流等方式，培养学生团队协作、共同探究的学习习惯。
3.运用比较、分类、归纳等方法，引导学生总结视图的特点、规律，提高学生的逻辑思维能力。
五、作业布置
为了巩固本章节所学知识，确保学生对视图的理解和应用能力得到有效提升，特布置以下作业：
1.完成课本第123页的练习题1、2、3，要求学生在完成过程中注意三视图的画法和转换方法，强化对视图概念的理解。
2.选择一个生活中的物体，如文具盒、水杯等，自行绘制其三视图，并尝试运用所学知识求解该物体的表面积和体积。此作业旨在培养学生的空间想象能力和几何计算能力。
4.结合实际生活中的例子，让学生体会数学与现实生活的联系，培养学生的应用意识和实践能力。
（三）情感态度与价值观
1.培养学生对数学学习的兴趣和热情，增强学生的自信心和自主学习能力。
2.引导学生认识到数学在科技发展、社会进步中的重要作用，树立正确的价值观。
3.培养学生严谨、细致的学习态度，提高学生的责任心和自律意识。
（五）总结归纳
1.教师引导学生回顾本节课所学内容，总结视图的概念、画法、转换方法及其在实际中的应用。

①主视图？ ②左视图？ ③俯视图？
·
单二击、此常处见编几辑何母体版标的题三样视的题三样视式图
自我尝试1
画出如图所示物体的主视图、 左视图、俯视图．
主视图
左视图
俯视图
单二击、此常处见编几辑何母体版标的题三样视式图
自我尝试2
单二击、此常处见编几辑何母体版标的题三样视式图
自我尝试2
单三击、此归处纳编小辑结母版标题样式
投影与视图的关系： 用正投影的方法绘制的物体在投影面上的图形，
称为物体的视图.
三个正投影
三视图（主视图、左视图、俯视图）
细节：看得见部分的轮廓线要画成实线， 特别留意圆锥的俯视图.
单四击、此反处馈编评辑价母版标题样式
1．下列立体图形中，主视图为矩形的是（ C ）
4．如图是由一个长方体和一个圆锥组成的 几何体，请你画出它的三视图.
主视图
左视图
俯视图
单四击、此反处馈编评辑价母版标题样式
5.根据下列主视图和俯视图，找出对应的物体.
（1）==>B； （2）==>A； （3）==>D； （4）==>C.
A.
B.
C.
D.
单四击、此反处馈编评辑价母版标题样式
2.将两个圆盘、一个茶叶桶、一个篮球模型和一个蒙古包模型 按如图所示的方式摆放在一起，其主视图是（ D ）
单四击、此反处馈编评辑价母版标题样式
3．如图，下面的几何体由一个正方体和两个圆柱体组成， 则它的左视图是（ D ）
A.
B.
C.
D.
单四击、此反处馈编评辑价母版标题样式
第五章 投影与视图
5.2 视图（1）
单一击、此温处故编知辑新母版标题样式

第5章视图与投影
5.2视图（一）
教学目标：
1．经历由实物抽象出几何体的过程，进一步发展空间观念。

2．会画圆柱、圆锥、球的三视图，体会这几种几何体与其视图之间的相互转化。

3．会画直棱柱（仅限于直三棱柱和直四棱柱）的三种视图，体会这几种几何体与其视图之间的相互转化。

4. 会根据三视图描述原几何体。

教学重点：掌握部分几何体的三视图的画法。

掌握直棱柱的三视图的画法。

能根据三视图描述原几何体。

教学难点：几何体与视图之间的相互转化。

培养空间想像观念。

课型：新授课
教学方法：观察实践法
想像，再抽象出这两个直棱柱的主视图，左视图和俯视图。

体，你能帮小明画出这个几何体的三视图
（对应
）
下图是正方体分割后的
况定出实物，最后便可
能力升华：
由三视图确定原实物小立方体的个
图、俯视图确定小立方体的个数由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图图中的数字表示垂直方向小正方体的A B C
D E
3 2 1
1 2
成学习内容的。

在。

2　视图第1课时【教学目标】知识与技能:1.探索基本几何体(圆柱、圆锥、球)与其三种视图(主视图、左视图、俯视图)之间的关系.2.会判断简单物体的三视图,发展合情推理能力和数学表达能力.过程与方法:经历由实物抽象出几何体的过程,进一步发展空间观念.情感态度与价值观:结合具体实例,初步体会视图在现实生活中的应用,感受数学与现实生活的密切联系,增强学生的数学应用意识.【重点难点】重点:会判断简单物体的三视图.难点:由实物抽象出几何体,判断简单物体的三视图.【教学过程】一、创设情境1.“横看成岭侧成峰,远近高低各不同.”一句中蕴含着怎样的数学道理?2.王明昨天买了一本字典,假如有一束平行光线从正面、左面、上面照射这本字典,得到正投影图形是什么?二、探索归纳1.如图,这个物体可以看做是由什么几何体组成的?2.假如一束平行光线从正面、左面、上面投射到物体上,你能想象出它的正投影吗?试着画出来.物体的正投影称为物体的视图,由此自然引出主视图、左视图、俯视图的定义,随之准确给出上述三种图形的名称.参照教材提供的几何体,提出问题:(1)图中物体的形状分别可以看成什么样的几何体?与同伴交流.(2)在图中分别找出上述几何体的主视图.(3)你能想象出(1)中各物体的左视图和俯视图吗?与同伴交流,请你试着画出来.(4)你能说出常见几何体的三种视图的特点吗?三、交流反思学生互相交流总结三视图的特点,主视图、左视图、俯视图的区别与内在的联系,及各自在合作交流学习过程中的体会与感受等.四、检测反馈1.“圆柱与球的组合体”如图所示,则它的三视图是( )2.下图是冰激凌模型图,它的三视图是( )五、布置作业课本P137　习题5.3　第1、2题六、板书设计视图1.探究2.归纳:3.练习:七、教学反思 通过课堂小组合作解决有关问题的过程,为学生提供展示自己聪明才智的机会,并且在此过程中更利于教师发现学生分析问题、解决问题的能力,以及思维的误区,以便指导今后的教学.课堂上要把激发学生学习热情和获得学习能力放在教学首位,通过运用各种启发、激励的语言,以及组织小组合作学习,帮助学生形成积极主动的求知态度. 注意改进的方面: 在小组讨论之前,应该留给学生充分的独立思考的时间,不要让一些思维活跃的学生的回答代替了其他学生的思考,掩盖了其他学生的疑问.教师应对小组讨论给予适当的指导,包括知识的启发引导、学生交流合作中需注意的问题等.关闭Word文档返回原板块。

§5—1 绘制三视图并标注尺寸教学过程学环节二、认识并绘制三视图思考：工程制图中，为什么要用三视图？而不用二视图，或者一个方向的投影呢？不同形状的物体在某个投影面所得到的投影完全相同。

因此，单一投影和二面投影不能完全表示物体的结构形状。

往往需要多个视图才能完整反映物体的几何形状。

1.三视图的概念及形成采用三个互相垂直相交的投影面(即正面投影面V、水平投影面H和侧面投影面W)建立一个三投影面体系，再采用正投影法将物体同时向三个投影面投影。

三视图的形成过程增加：请同学们动手制作一个三视图空间坐标系2.三视图的位置关系和投影规律（1）三视图间的位置关系俯视图在主视图的正下方，左视图在主视图的正右方。

（2）视图之间的对应关系主视图—形体高度尺寸和左右方向的长度尺寸。

俯视图—形体长度尺寸和前后方向的宽度尺寸。

左视图—形体高度尺寸和前后方向的宽度尺寸。

投影规律口诀：长对正、高平齐、宽相等3.三视图的绘制P116马上行动：理解三视图的形成过程，为绘制三视图打下基础。

掌握三视图的一般绘图规则让学生找一张纸制作空间坐标系，加深学生对于三视图位置的认识展示学生绘制的三视图，找出学生增加：根据三视图还原物体三、形体的尺寸标注马上行动：阅读教材P118119，学习形体的尺寸标注方法。

1.尺寸标注的基本要求a.正确，尺寸注写必须符合国家标准；b.完整，齐全，不遗漏，不重复；c.清晰，整齐，清晰，便于读图;d.合理，符合加工要求。

2.标注尺寸的三要素完整的尺寸标注应该包括：a.尺寸界线；b.尺寸线；c.尺寸数字。

a尺寸标注三要素——尺寸界线1)尺寸界线由细实线绘制2)轮廓线轴线对称中心线b尺寸标注三要素——尺寸线1)尺寸线由细实线绘制2)尺寸线必须单独画出3)箭头为实心细长箭头c尺寸标注三要素——尺寸数字绘制简单物体的三视图学习如何给形体的尺寸标注的易错点因为作图是在平面上完成，但是作为读图的人一定要知道物体的基本形态，所以通过三视图还原物体是基本能力1)尺寸表示形体的真实大小。

5.2.1视图教学设计观察下列图片，猜一猜他们两个的关系？从正面正投影得到：2．如果平行光线从左面投影到图中的物体上，情况又如何？如果平行光线从上面投射到图中的物体上呢？从左面正投影3.如图，假设有一束平行光线从上面投射到图中的物体上，能想象出它在这书平行光线下的正投影吗？从上面正投影归纳总结：像这样，用正投影的方法绘制的物体在投影面上的图形，称为物体的_______．从正面得到的视图叫做_________，从左面得到的视图叫做_________，从上面得到的视图叫做_________．问题：观察主视图,左视图,俯视图你发现了什么规律？1．主视图反映物体的左右长度和上下高度，俯视图反映物体的___________和前后宽度，左视图反映物体的___________和___________，因此在画三视图时，主、俯视图要做到______对正，主、左视图要______平齐，左、俯视图要______相等；2．在画视图时，看得见部分的轮廓线要画成_____线，看不见部分的轮廓线要画成_____线．三视图的画法步骤：(1)先画互相垂直的辅助线XY'，ZY；(2)确定主视图的位置，画出主视图；(3)根据“长对正”与几何体宽度，画出俯视图；(4)根据“高平齐”与“宽相等”画出左视图；(5)擦去辅助线．议一议1.图中物体的形状分别可以看成什么样的几何体甲为圆柱；乙为圆锥；丙为球.2.在图中分别找出下列几何体的主视图：甲的主视图为：A;乙的主视图为：E;丙的主视图为：C甲的左视图为：A;乙的左视图为：E;丙的左视图为：C甲的俯视图为：C;乙的俯视图为：C;丙的俯视图为：C(3)请完成下表.想一想：如图1是一个蒙古包的照片．小明认为这个蒙古包可以看成图2所示的几何体？你能帮小明画出这个几何体的三种视图吗？方法指导：蒙古包下面是圆柱，上面是圆锥．解：蒙古包可看成圆锥、圆柱同底的组合图形．1. 关于如图所示的水缸，下列说法正确的是（）A. 它的俯视图是圆B. 它的主视图与左视图相同C. 它的三种视图都相同D. 它的主视图与俯视图都是圆2．如图所示的几何体是由一个圆柱体和一个长方体组成的，则这个几何体的俯视图是()3.如图所示是一个立体图形的三视图，请根据视图说出立体图形的名称 .4.一张桌子摆放若干碟子，从三个方向上看，三种视图如下图所示，则这张桌子上共有个碟子.5．如图，从不同方向看下面左图中的物体，右图中三个平面图形分别是从哪个方向看到的？。

（说课稿）学校：贺兰一中班级：初三（2）班教师：罗海军义务教育课程标准教科书九年级数学上册5.2《视图》说课稿第3课时贺兰一中罗海军一、教材分析1.1、教材的地位和作用《视图》是北师大版九年级上册第五章第二节的内容，是在学习空间几何体结构特征和投影之后的情况下教学的。

三视图是空间几何体的一种表示形式，是立体几何的基础之一。

学好三视图有利于培养学生空间想象能力，几何直观能力，有利于培养学生学习立体几何的兴趣，为高中的后续学习打下基础 .因此我将从投影的角度加深对三视图概念的理解和由三视图想象实物模型，并画出模型草图作为本节课的重点.1.2、教学目标设计知识与技能：（1）能由三视图想象出简单几何体的形状，并且能画出草图。

（2）能画出除了圆柱、圆锥、正方体等几何体外，其它较复杂几何体的三视图。

（3）进一步理解三视图与几何体之间的联系。

过程与方法：经历探索三视图还原实物图的过程，掌握由平面到空间的转换方法，进一步发展空间想象能力和综合分析能力。

情感态度与价值观：培养学生学习立体几何的兴趣以及勇于探索实践的精神，体会本节知识对后续知识学习以及未来工作、生活的重要作用。

1.3、教学重点、难点分析教学重点：由三视图想象实物模型，并画出模型草图。

教学难点：由三视图还原出实物图二、学生情况分析本节课是视图的第三课时，主要内容是学习如何根据三视图来想象几何体的形状，并且画出草图。

由于前面两节课学生已经学习了圆柱、圆锥、球及其组合图形的三种视图，初步了解了视图的作用，为本节课的学习打下了一定的基础。

本课时的学习将运用逆向思维，思维形式也已经从一般的操作层面上升到了理性思考的层面，对平面与空间的感受更加深刻，学生在前面的观察、操作、想象、推理的基础上形成的空间观念为学好本课提供了可能。

三、本节课设计思想如何培养学生的空间想象和几何直观能力，在“数学课程标准”中，“立体几何初步”突出了直观感知，操作确认，度量计算等探索、研究几何的过程,在学习必修课程阶段以直观感知，操作确认为重点,强调建立和提升学生的空间想象力和几何直观能力.在教学中充分利用教科书“思考”、“探究”栏目中提出的问题，让学生亲身实践，动手作图来完成.通过大量实物、模型展示，动手制作模型以及计算机模拟等手段可以解决教师“口说无凭”的尴尬境地.三视图是一个从实物模型到平面图形的过程，是一个从具体到抽象再到具体的过程，是提高空间想象力的有效手段.四、教法、学法特点分析1.教法分析：学生直接经验和亲身经历，以学生的亲手操作、亲历情景、亲身体验为基础，强调学生的全员参与和全程参与。