哈工大材料力学试卷及答案资料

一、填空题：请将正确答案写在划线内（每空1分，计16分） ⒈ 工程构件正常工作的条件是 ――――――――――――、、――――――――――――、―――――――――――――。

⒉ 工程上将延伸律------- δ的材料称为脆性材料。

⒊ 矩形截面梁横截面上最大剪应力max τ出现在―――――――――――各点，其值=τmax -------------。

4．平面弯曲梁的q 、F s 、M 微分关系的表达式分别为--------------、、-------------、、 ----------------。

5．四个常用的古典强度理论的表达式分别为―――――――――――――――――、―――――――――――――――――――――、 ――――――――――――――、―――――――――――――――――――――――――――――――――。

6．用主应力表示的广义虎克定律为 ――――――――――――――――――――― ；――――――――――――――――――――――；－―――――――――――――――――――――――。

二、单项选择题⒈ 没有明显屈服平台的塑性材料，其破坏应力取材料的――――――――――――。

⑴ 比例极限p σ； ⑵ 名义屈服极限2.0σ； ⑶ 强度极限b σ； ⑷ 根据需要确定。

２． 矩形截面的核心形状为----------------------------------------------。

⑴ 矩形； ⑵ 菱形； ⑶ 正方形； ⑷三角形。

3． 杆件的刚度是指――――――――――――――－。

⑴ 杆件的软硬程度； ⑵ 杆件的承载能力； ⑶ 杆件对弯曲变形的抵抗能力； ⑷ 杆件对弹性变形的抵抗能力；4. 图示二向应力单元体，如剪应力改变方向，则―――――――――――――。

⑴ 主应力的大小和主平面的方位都将改变；⑵ 主应力的大小和主平面的方位都不会改变； ⑶ 主应力的大小不变，主平面的方位改变； ⑷ 主应力的大小改变，主平面的方位不变。

一、解释下列名词滞弹性：在外加载荷作用下，应变落后于应力现象。

静力韧度：材料在静拉伸时单位体积材科从变形到断裂所消耗的功。

弹性极限：试样加载后再卸裁，以不出现残留的永久变形为标准，材料能够完全弹性恢复的最高应力。

比例极限：应力—应变曲线上符合线性关系的最高应力。

二、金属的弹性模量主要取决于什么?为什么说它是一个对结构不敏感的力学姓能?答案：金属的弹性模量主要取决于金属键的本性和原子间的结合力，而材料的成分和组织对它的影响不大，所以说它是一个对组织不敏感的性能指标，这是弹性模量在性能上的主要特点。

改变材料的成分和组织会对材料的强度(如屈服强度、抗拉强度)有显著影响，但对材料的刚度影响不大。

三、什么是包辛格效应，如何解释，它有什么实际意义?答案：包辛格效应就是指原先经过变形，然后在反向加载时弹性极限或屈服强度降低的现象。

特别是弹性极限在反向加载时几乎下降到零，这说明在反向加载时塑性变形立即开始了。

包辛格效应可以用位错理论解释。

第一，在原先加载变形时，位错源在滑移面上产生的位错遇到障碍，塞积后便产生了背应力，这背应力反作用于位错源，当背应力(取决于塞积时产生的应力集中)足够大时，可使位错源停止开动。

背应力是一种长程(晶粒或位错胞尺寸范围)内应力，是金属基体平均内应力的度量。

因为预变形时位错运动的方向和背应力的方向相反，而当反向加载时位错运动的方向与原来的方向相反了，和背应力方向一致，背应力帮助位错运动，塑性变形容易了，于是，经过预变形再反向加载，其屈服强度就降低了。

这一般被认为是产生包辛格效应的主要原因。

其次，在反向加载时，在滑移面上产生的位错与预变形的位错异号，要引起异号位错消毁，这也会引起材料的软化，屈服强度的降低。

实际意义：在工程应用上，首先是材料加工成型工艺需要考虑包辛格效应。

其次，包辛格效应大的材料，内应力较大。

另外包辛格效应和材料的疲劳强度也有密切关系，在高周疲劳中，包辛格效应小的疲劳寿命高，而包辛格效应大的，由于疲劳软化也较严重，对高周疲劳寿命不利。

材料力学习题答案2-4 a)MPa 15MPa,10-=='''y x x τσb)MPa 3.7MPa,3.47=='''y x x τσ c)MPa 65MPa,5.12-=-='''y x x τσd)MPa 6.60MPa,35-=='''y x x τσ e)MPa 5.20MPa,49.0=='''y x x τσf)MPa 0MPa,2.38=-='''y x x τσ2-6 a) MPa 32,0219MPa,7MPa,57max 21='=-==τασσσb)MPa 32,0219MPa,7MPa,57max 21='-=-==τασσσ c)MPa 25,45MPa,25MPa,25max 21==-==τασσσ d)MPa 2.41,9537MPa,2.71MPa,2.11max 21='=-==τασσσe) MPa 7.44,7113MPa,7.84MPa,7.4max 21='=-==τασσσ f)MPa 32,0219MPa,27MPa,37max 21='-=-==τασσσ 2-8 a) 略略；；))cos ),cos 1(,0),cos 1(0max 0320c b x στθσσσθσσ=-==+=2-10 1071=σMPa ，02=σ，203-=σMPa2-11 3.43-=xy τMPa ，3.43-''y x τMPa ，50='y σMPa2-137.841=σ MPa ，202=σMPa ，7.43-=σMPa ，1001=I MPa ，8002=I （MPa ）2，240003=I （MPa ）32-14 a)701=σ MPa ，602=σMPa ，303=σMPa ，70max =σMPa ，20max =τMPab) 501=σ MPa ，502=σMPa ，303=σMPa ，50max =σMPa ，10max =τMPa3-1 εx =0,εy =c ，εz =kx +iy +2gz ，γxy =b ，γyz =ix +2fy +jz +d ，γzx =2ex +iy +kz 。

材料力学习题(7)第十二章哈工业大材料力学本科生试卷和课后题目材料力学习题第12章12-1 一桅杆起重机，起重杆AB的横截面积如图所示。

钢丝绳的横截面面积为10mm2。

起重杆与钢丝的许用力均为[?]?120MPa，试校核二者的强度。

习题2-1图习题12-2图12-2 重物F=130kN悬挂在由两根圆杆组成的吊架上。

AC是钢杆，直径d1=30mm，许用应力[?]st=160MPa。

BC是铝杆，直径d2= 40mm, 许用应力[?]al= 60MPa。

已知ABC为正三角形，试校核吊架的强度。

12-3 图示结构中，钢索BC由一组直径d =2mm的钢丝组成。

若钢丝的许用应力[?]=160MPa,横梁AC单位长度上受均匀分布载荷q =30kN/m作用，试求所需钢丝的根数n。

若将AC改用由两根等边角钢形成的组合杆，角钢的许用应力为[?] =160MPa，试选定所需角钢的型号。

12-4 图示结构中AC为钢杆，横截面面积A1=2cm2；BC杆为铜杆，横截面面积A2=3cm2。

[?]st = 160MPa，[?]cop = 100MPa，试求许用载荷[F]。

习题12-3图习题12-4图12-5 图示结构，杆AB为5号槽钢，许用应力[?] = 160MPa，杆BC为hb= 2的矩形截面木杆，其截面尺寸为b = 5cm, h = 10cm,许用应力[?] = 8MPa，承受载荷F = 128kN，试求：（1）校核结构强度；（2）若要求两杆的应力同时达到各自的许用应力，两杆的截面应取多大？习题12-5图习题12-6图12-6 图示螺栓，拧紧时产生?l = 0.10mm的轴向变形，试求预紧力F，并校核螺栓强度。

已知d1=8mm, d2=6.8mm, d3=7mm, l1=6mm, l2=29mm, l3=8mm; E=210GPa,[?]=500MPa。

12-7 图示传动轴的转速为n=500r/min，主动轮1输入功率P1=368kW，从动轮2和3分别输出功率P2=147kW和P3=221kW。

一、填空题：请将正确答案写在划线内（每空1分，计16分）⒈ 工程构件正常工作的条件是 ――――――――――――、、――――――――――――、―――――――――――――。

⒉ 工程上将延伸律------- δ的材料称为脆性材料。

⒊ 矩形截面梁横截面上最大剪应力max τ出现在―――――――――――各点，其值=τmax -------------。

4．平面弯曲梁的q 、F s 、M 微分关系的表达式分别为--------------、、-------------、、----------------。

5．四个常用的古典强度理论的表达式分别为―――――――――――――――――、―――――――――――――――――――――、――――――――――――――、―――――――――――――――――――――――――――――――――。

6．用主应力表示的广义虎克定律为 ――――――――――――――――――――― ；――――――――――――――――――――――；－―――――――――――――――――――――――。

二、单项选择题⒈ 没有明显屈服平台的塑性材料，其破坏应力取材料的――――――――――――。

⑴ 比例极限p σ； ⑵ 名义屈服极限2.0σ；⑶ 强度极限b σ； ⑷ 根据需要确定。

２． 矩形截面的核心形状为----------------------------------------------。

⑴ 矩形； ⑵ 菱形； ⑶ 正方形； ⑷三角形。

3． 杆件的刚度是指――――――――――――――－。

⑴ 杆件的软硬程度； ⑵ 杆件的承载能力；⑶ 杆件对弯曲变形的抵抗能力； ⑷ 杆件对弹性变形的抵抗能力； 4. 图示二向应力单元体，如剪应力改变方向，则―――――――――――――。

⑴ 主应力的大小和主平面的方位都将改变；⑵ 主应力的大小和主平面的方位都不会改变；⑶ 主应力的大小不变，主平面的方位改变；⑷ 主应力的大小改变，主平面的方位不变。

哈工大2002年春季学期题号-一--二二三四五六七八九附加分总分得分班级姓名一、单选或多选题（每小题3分，共8小题24分）1.某点为平面应力状态（如图所示），该点的主应力分别为A = 50MPa、二2 =0 、3=° -B二50MPa、二2=50 MPa、匚3= 0；C -1 =0、匚 2 二50 MPa、■T 3 = 0 -D -1 =0、二2 = 0、-3 : "50MPa。

正确答案是___________50er (MPtL)2.关于弹性体受力后某一方向的应力与应变关系有如下论述: 正确的是。

A 有应力一定有应变，有应变不一定有应力；B 有应力不一定有应变，有应变不一定有应力；C 有应力不一定有应变，有应变一定有应力；D 有应力一定有应变，有应变一定有应力。

3•下面有关体积应变的几个论述，正确的是________________A 与平均应力成正比；B与平均应力成反比；C与三个相垂直面上的正应力之和有关；D与平均应力无关。

4.下面有关应变能的几个论述，正确的是A与载荷的加载次序有关，与载荷的最终值无关；B与载荷的加载次序无关，与载荷的最终值无关；C与载荷的加载次序有关，与载荷的最终值有关；D 与载荷的加载次序无关，与载荷的最终值有关。

5•关于斜弯曲变形的下述说法，正确的是_________________A中性层与挠曲线所在的面正交；B中性轴过横截面的形心；C挠曲线在载荷作用面内；D挠曲线不在载荷作用面内。

A 单位力（广义）只能加在载荷作用点处；B单位力（广义）只能加在欲求位移的点处；C只能加单位集中力；D 只能加单位集中力偶。

正确的是_____________ 。

7 •压杆的稳定性，A 与压杆所承受的轴向压力大小有关；B与压杆的临界力大小有关；C 与压杆所承受的轴向压力大小无关；D 与压杆的临界力大小无关。

正确答案是___________& 自由落体冲击时的动荷系数，A 与被冲击物的刚度有关；B与自由落体下落的高度有关；C 与被冲击物的刚度无关；D 与冲击刚发生时，自由落体下落的速度有关。

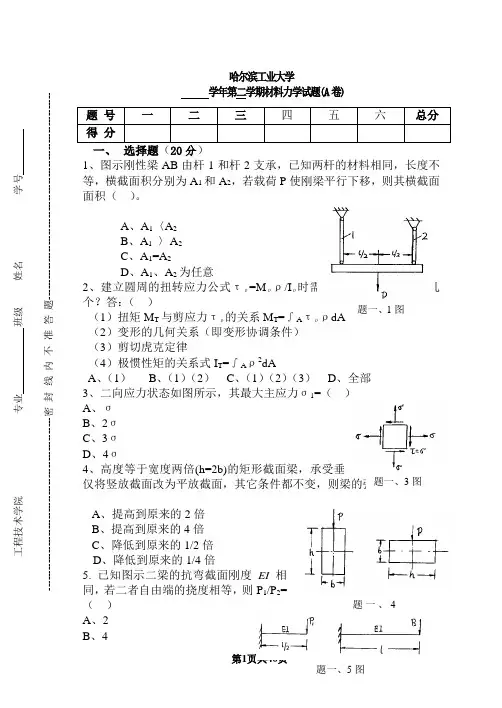
哈尔滨工业大学学年第二学期材料力学试题(A 卷)一、 选择题（20分）1、图示刚性梁AB 由杆1和杆2支承，已知两杆的材料相同，长度不等，横截面积分别为A 1和A 2，若载荷P 使刚梁平行下移，则其横截面面积（ ）。

A 、A 1〈A 2B 、A 1 〉A 2C 、A 1=A 2D 、A 1、A 2为任意2、建立圆周的扭转应力公式τρ=M ρρ/I ρ时需考虑下列因素中的哪几个？答：（ ）（1）扭矩M T 与剪应力τρ的关系M T =∫A τρρdA （2）变形的几何关系（即变形协调条件） （3）剪切虎克定律（4）极惯性矩的关系式I T =∫A ρ2dA A 、（1） B 、（1）（2） C 、（1）（2）（3） D 、全部 3、二向应力状态如图所示，其最大主应力σ1=（ ） A 、σ B 、2σ C 、3σ D 、4σ4、高度等于宽度两倍(h=2b)的矩形截面梁，承受垂直方向的载荷，若仅将竖放截面改为平放截面，其它条件都不变，则梁的强度（）A 、提高到原来的2倍B 、提高到原来的4倍C 、降低到原来的1/2倍D 、降低到原来的1/4倍5. 已知图示二梁的抗弯截面刚度EI 相同，若二者自由端的挠度相等，则P 1/P 2=（ ）A 、2B 、4题 号 一 二 三 四 五 六 总分 得 分题一、3图 工程技术学院 _______________专业 班级 姓名____________ 学号---------------------------------------------------密 封 线 内 不 准 答 题-------------------------------------------------------------题一、4题一、1图C 、8D 、16二、作图示梁的剪力图、弯矩图。

（１５分）三、如图所示直径为d 的圆截面轴，其两端承受扭转力偶矩m 的作用。

设由实验测的轴表面上与轴线成450方向的正应变，试求力偶矩m 之值、材料的弹性常数E 、μ均为已知。

哈工大材料力学(张少实版)部分课后习题答案第一章介绍1.1 弹性体的概念弹性体是指在外力作用下能够发生形变，而形变消失后，恢复到原来的形状和大小的物质。

弹性体具有以下特性：•保持原有形状和大小：在外力作用下发生形变，但形变消失后恢复到原来的形状和大小。

•快速恢复到原始状态：形变消失后，弹性体迅速恢复到初始状态。

•应变与应力成正比：弹性体的应变与应力之间存在线性关系。

1.2 描述力学行为的基本物理量描述力学行为的基本物理量有应力、应变和模量等。

•应力（Stress）：指单位面积内的力。

•应变（Strain）：表示形变的程度。

•模量（Modulus）：用来描写物质的力学性质。

1.3 弹性常数弹性常数用来描述物质的弹性性质，常见的弹性常数包括弹性模量、剪切模量和泊松比等。

•弹性模量（Elastic modulus）：描述材料受力时的弹性性质。

•剪切模量（Shear modulus）：描述材料抗剪切变形的能力。

•泊松比（Poisson’s ratio）：描述材料在拉伸变形时横向的变形程度。

第二章单轴拉伸与压缩2.1 弹性模量弹性模量（Elastic modulus）也称为杨氏模量（Y oung’s modulus），表示单位面积内的应力与应变之间的比例关系。

弹性模量的计算公式为：E = σ / ε其中，E为弹性模量，σ为应力，ε为应变。

2.2 剪切应变与剪切模量剪切应变（Shear strain）用来描述材料在受剪切力作用下产生的变形。

剪切应变的计算公式为：γ = Δx / L其中，γ为剪切应变，Δx为剪切变形量，L为材料的长度。

剪切模量（Shear modulus）表示材料抗剪切变形的能力。

剪切模量的计算公式为：G = τ / γ其中，G为剪切模量，τ为剪切应力。

2.3 泊松比泊松比（Poisson’s ratio）表示材料在拉伸变形时横向的变形程度。

泊松比的计算公式为：ν = -εt / εl其中，ν为泊松比，εt为横向应变，εl为纵向应变。

材料力学习题第2章2-1 试求出图示各杆件中Ⅰ—Ⅰ截面上的内力。

2-2图示矩形截面杆，横截面上正应力沿截面高度线性分布，截面顶边各点处的正应力均为MPa100max=σ，底边各点处的正应力均为零。

杆件横截面上存在何种内力分量，并确定其大小（C点为截面形心）。

2-3 试指出图示各单元体表示哪种应力状态。

2-4 已知应力状态如图所示（应力单位为MPa），试用解析法计算图中指定截面的应力。

2-5 试作应力圆来确定习题2-4图中指定截面的应力。

2-6已知应力状态如图所示（应力单位为MPa ），试用解析法求：（1）主应力及主方向；（2）主切应力及主切平面；（3）最大切应力。

2-7 已知应力状态如习题2-6图所示，试作应力圆来确定：（1）主应力及主方向； （2）主切应力及主切平面；（3）最大切应力。

2-8已知构件内某点处的应力状态为两种应力状态的叠加结果，试求叠加后所得 应力状态的主应力、主切应力。

2-9图示双向拉应力状态，σσσ==y x 。

试证明任一斜截面上的正应力均等于σ，而切应力为零。

2-10 已知K 点处为二向应力状态，过K 点两个截面上的应力如图所示（应力单位为MPa ）。

试分别用解析法与图解法确定该点的主应力。

2-11 一点处的应力状态在两种坐标系中的表示方法分别如图 a)和b)所示。

试确定未知的应力分量y y x xy '''σττ、、的大小与方向。

2-12 图示受力板件，试证明尖角A 处各截面的正应力与切应力均为零。

2-13 已知应力状态如图所示（单位为MPa ），试求其主应力及第一、第二、第三不变量321II I 、、。

2-14 已知应力状态如图所示（单位为MPa ），试画三向应力圆，并求主应力、最大正应力与最大切应力。

第3章3-1 已知某点的位移分量u = A ， v = Bx +Cy +Dz ， w = Ex 2+Fy 2+Gz 2+Ixy +Jyz +Kzx 。

哈工大2007年材料力学期末考试A卷附有答案1. 单项选择题: (共8小题，每小题3分，总分24分) 1-1. 以下关于虚功和虚位移的论述中正确的是（ b ）.A. 力F在其虚位移d上所作的功为/2Fd B. 虚位移必须满足位移约束条件C. 虚位移引起的系统能量变化比真实位移引起的小 D.虚功只能由外力引起1-2. 以下( a ) 不是疲劳的特征.A. 破坏时名义应力值等于材料的静强度值B. 构件需要经过一定的应力循环才破坏C. 破坏断面明显划分为光亮区域与颗粒状的粗糙区域D. 破坏是脆性断裂1-3. 关于面积相同的圆形和正方形截面（如图1-3所示），对各自主轴x的抗弯能力，以下描述正确的是（ a ）.A. ()()>.a bb a>. B. ()()C. ()()=. D. 两者相差超过50%a b图1-3 图1-41-4. 图1-4所示结构的静不定次数是（ c ）A. 1 次B. 2 次C. 3次D.4次1-5. 如图1-5所示，梁在其中点处受一集中载荷F。

假设梁的横截面宽度保持不变，若按等强度观点设计梁的横截面高度，那么梁的大致形状是（ c ）图1-51-6. 直径为d的圆形截面和边长为a的正方形截面对其各自形心轴的惯性半径分别是（ a ）.A. /4d和/(23)aB. /(22)ad和/6C. /4ad和/2D. /(22)d和/(23)a1-7. 以下关于第三和第四强度理论的论述中正确的是（a ）A. 满足第三强度理论必然满足第四强度理论B. 满足第四强度理论必然满足第三强度理论C. 有时（A）成立，有时（B）成立D. 两强度理论并无必然联系1-8. 关于梁的弯曲，以下不正确的是( c )A. 各类挠曲线方程都是分段成立的B. 在各段上分布外载、剪力和弯矩函数依次越来越光滑C. 应用22=时可以用剪力匹配条件来确定未知参数d v dx M x/()D. 挠度函数()dv x dx总是连续的v x及()/2. 图2所示梁AC刚度为EI。

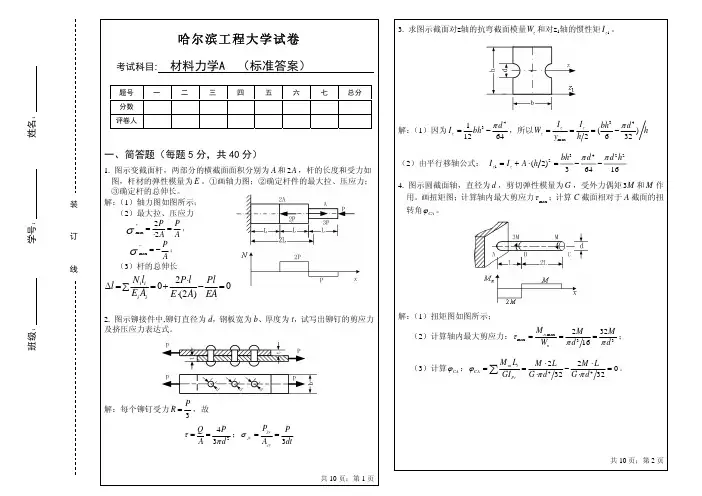
哈尔滨工程大学试卷考试科目:材料力学B一简答题（每题5分，共40分）1、等截面圆杆受力如图，弹性模量200E GPa =，若杆的总伸长不允许超过1mm ，试求杆的直径的最小值。

60kN20kN200mm200mm2、空心圆轴横截面上扭矩为n M ，方向如图，内、外径分别为d 和D ，在图上画出扭转剪应力分布规律图，并写出内壁上点A 的扭转剪应力表达式。

dDAonM 共9页；第1页3、螺栓联接结构受力如图，两板宽均为b 、厚均为t 。

若材料的拉（压）、剪切、挤压许用应力分别为[]σ、[]τ、jy σ⎡⎤⎣⎦。

写出该联接件的强度条件。

dtt PP4、求图示图形的形心位置及对形心轴c y 轴的惯性矩yc I 。

（图中尺寸单位为mm ）30cy C cz 3030909030共9页；第2页班级：学号：姓名：装订线题号一二三四五六总分分数评卷人5、圆轴扭转时，测得与轴线呈45 角方向上的线应变45εε=-，拉压弹性模量E 和泊松比 已知。

试求横截面上的剪应力τ。

eM eM 456、写出弯曲对称循环情况下构件的持久极限计算表达式，并说明各量的含义。

共9页；第3页7、重量为Q 的重物自由下落在图示刚架的C 点，设材料的抗弯刚度EI 和抗弯截面模量W 均已知，且已知C 点的静变形343j Qa EI ∆=。

试求冲击时刚架内的最大正应力（轴力影响不考虑）。

CBAaaHQ8、试绘制某塑性材料的临界应力总图(中长杆用直线型经验公式)，并标出各段计算临界应力的公式。

共9页；第4页班级：学号：姓名：装订线二、画出图示梁的剪力图、弯矩图，并确定max Q 和maxM。

(12分)BAa aCq2qaqa212qa 212qa max Q qa=2max12Mpa =QMxx共9页；第5页三、如图圆截面轴。

已知2.n M kN m =，11P kN =，2 1.5P kN =，[]150MPa =，横截面直径80d mm =。

哈工大2018年春季学期材料力学期末考试参考答案一、(20分)参考答案方法1：BC 段均布载荷导致：θ1A =−q (2l )324EI =−ql 33EI ;v 1D =−5q (2l )4384EI =−80ql 4384EI 。

AB 段悬臂梁，BC 段刚化导致：θ2A =ql 36EI ;v 2D =0。

AB 段刚化，其上均布载荷等效至B 点，由弯矩ql 22导致：θ3A =ql 222l 3EI =ql 33EI ;v 3D =ql 22(2l )216EI =ql 48EI叠加后得到：θA =θ1A +θ2A +θ3A =ql 36EI(逆时针);此项合10分v D =v 1D +v 2D +v 3D =−ql 412EI (向下)。

此项合10分方法2：叠加法θq B =q (2l )324EI =ql 33EI (↻);θM B =q2l 2⋅2l 3EI =ql 33EI(↺)因此θB =0，θA =θB +ql 36EI =ql 36EI (↺,逆时针)此项合10分v D =5q (2l )4384EI −12ql 2⋅(2l )216EI =5ql 424EI −ql 48EI =ql 412EI (↓,向下)此项合10分**若有用其它方法求解的，均按θA (10分)，v D (10分)处理。

二、(24分)参考答案此为一次静不定问题，取HJFl l 1(a)(b)(c)(d)J（1）力法方程:X 1δ11+∆1F =0中与静不定判定一起合为4分图(c)自乘:δ11=1⋅1⋅l EA +1EI (12l ⋅l ⋅23l +l ⋅l ⋅l )=l 38EI +4l 33EI =35l 324EI 5分图(a+b 与c)图乘:∆1F =−1EI 12l ⋅l 2⋅Fl 2+1EI (l ⋅l ⋅Fl +l 2⋅Fl ⋅34l )=−Fl 38EI +11Fl 38EI =5Fl 34EI 5分求解得X 1=−5Fl 34EI 35l 324EI =−67F (压)2分（2）为求C 截面转角，在C 施加逆时针单位弯矩(见图(d))θC =−12l 2⋅Fl 2⋅1EI +l ⋅Fl ⋅1EI +l ⋅l ⋅1EI X 1=−Fl 28EI +Fl 27EI =Fl 256EI(逆时针↺)8分三、(20分)参考答案解：1）利用扭矩平衡求出F 值：F cos (α)D 2=m x F =2m x D cos (α)=2×20×1030.4cos (20o )=106.4kN 4分2)F sin (α)导致弯矩：M z =Fl sin (α)4=106.4×103×1×sin (20o )4=9.098kN ⋅m ;4分3)F cos (α)导致弯矩：M y =Fl cos (α)4=106.4×103×1×cos (20o )4=25.0kN ⋅m ;4分导致扭矩：T =−F cos (α)D 2=−106.4×103×cos (20o )×0.42=−20.0kN ⋅m 2分4)利用第四强度理论：σr 4=1W z √M 2z +M 2y +0.75T 2=1πd 3/32√(9.098)2+(25.0)2+0.75202=31.75kN ⋅m πd 3/32≤[σ]d 3≥31.75kN ⋅m π[σ]/32=32×31.75×103π200×1065分d ≥11.74cm取轴的直径为11.74cm 。

一、填空题：请将正确答案写在划线内（每空1分，计16分）⒈ 工程构件正常工作的条件是 ――――――――――――、、――――――――――――、―――――――――――――。

⒉ 工程上将延伸律------- δ的材料称为脆性材料。

⒊ 矩形截面梁横截面上最大剪应力max τ出现在―――――――――――各点，其值=τmax -------------。

4．平面弯曲梁的q 、F s 、M 微分关系的表达式分别为--------------、、-------------、、 ----------------。

5．四个常用的古典强度理论的表达式分别为―――――――――――――――――、―――――――――――――――――――――、 ――――――――――――――、―――――――――――――――――――――――――――――――――。

6．用主应力表示的广义虎克定律为 ――――――――――――――――――――― ；――――――――――――――――――――――；－―――――――――――――――――――――――。

二、单项选择题⒈ 没有明显屈服平台的塑性材料，其破坏应力取材料的――――――――――――。

⑴ 比例极限p σ； ⑵ 名义屈服极限2.0σ；⑶ 强度极限b σ； ⑷ 根据需要确定。

２． 矩形截面的核心形状为----------------------------------------------。

⑴ 矩形； ⑵ 菱形； ⑶ 正方形； ⑷三角形。

3． 杆件的刚度是指――――――――――――――－。

⑴ 杆件的软硬程度； ⑵ 杆件的承载能力；⑶ 杆件对弯曲变形的抵抗能力；⑷ 杆件对弹性变形的抵抗能力；4. 图示二向应力单元体，如剪应力改变方向，则―――――――――――――。

⑴ 主应力的大小和主平面的方位都将改变；⑵ 主应力的大小和主平面的方位都不会改变；⑶ 主应力的大小不变，主平面的方位改变；⑷ 主应力的大小改变，主平面的方位不变。