20141206二次函数与圆综合试题

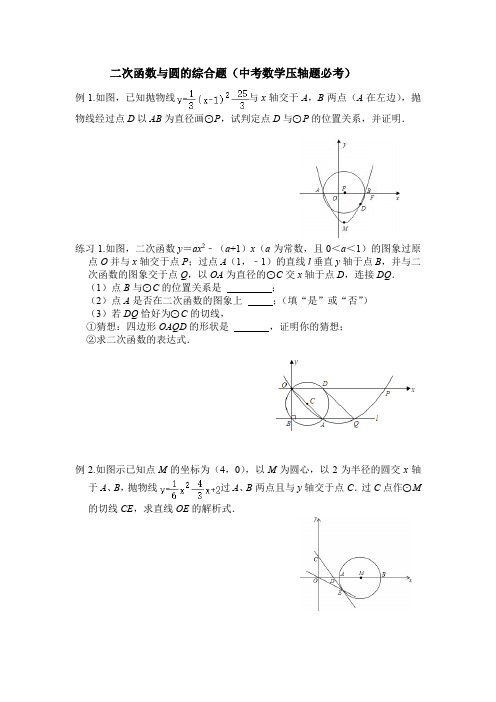
二次函数与圆的综合题（中考数学压轴题必考）例1.如图，已知抛物线与x轴交于A，B两点（A在左边），抛物线经过点D以AB为直径画⊙P，试判定点D与⊙P的位置关系，并证明．练习1.如图，二次函数y＝ax2﹣（a+1）x（a为常数，且0＜a＜1）的图象过原点O并与x轴交于点P；过点A（1，﹣1）的直线l垂直y轴于点B，并与二次函数的图象交于点Q，以OA为直径的⊙C交x轴于点D，连接DQ．（1）点B与⊙C的位置关系是；（2）点A是否在二次函数的图象上；（填“是”或“否”）（3）若DQ恰好为⊙C的切线，①猜想：四边形OAQD的形状是，证明你的猜想；②求二次函数的表达式．例2.如图示已知点M的坐标为（4，0），以M为圆心，以2为半径的圆交x轴于A、B，抛物线过A、B两点且与y轴交于点C．过C点作⊙M 的切线CE，求直线OE的解析式．练习2.平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴，设平行于x轴的直线交抛物线y＝﹣x2﹣x+2于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径；若不存在，请说明理由．练习3.如图，抛物线y＝﹣x2﹣x+2与x轴交于A（﹣4，0），B（2，0），与y 轴交于点C（0，2）．以AB为直径作⊙M，直线经过点E（﹣1，﹣5），并且与⊙M相切，求该直线的解析式．练习4.如图，抛物线y＝﹣x2+x+2．经过A、B、C三点，A点坐标为（4，0），B点坐标为（﹣1，0），以AB的中点P为圆心，AB为直径作⊙P的正半轴交于点C，M为抛物线的顶点，试说明直线MC与⊙P的位置关系，并证明你的结论．练习5.如图，抛物线与x轴交于A、B两点，与y轴交于C点．以AB为直径作⊙M．（1）求出M的坐标并证明点C在⊙M上；（2）若P为抛物线上一动点，求出当CP与⊙M相切时P的坐标；练习6.在平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴于点C，过点C作圆的切线交x轴于点D．（1）求点C的坐标和过A，B，C三点的抛物线的析式；（2）求点D的坐标：（3）设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径，若不存在，请说明理由．练习7.如图，在平面直角坐标系中，已知OA＝n，OC＝m，⊙M与y轴相切于点C，与x轴交于A，B两点，∠ACD＝90°，抛物线y＝ax2+bx+c经过A，B，C三点．（1）求证：∠OCA＝∠OBC；（2）若A（x1，0），B（x2，0），且x1，x2满足x1+x2＝5，x1•x2＝4，求点C 的坐标和抛物线的解析式；（3）若△ACD≌△ABD，在四边形ABDC内有一点P，且点P到四边形四个顶点的距离之和P A+PB+PC+PD最小，求此时距离之和的最小值及P点的坐标（用含n的式子表示）．练习8.已知二次函数y＝mx2+（m﹣3）x﹣3（m＞0）（1）求证：它的图象与x轴必有两个交点；（2）这条抛物线与x轴交于两点A、B（A在B左），与y轴交于点C，顶点为D，sin∠ABD＝，⊙M过A、B、C三点，求⊙M的面积；（3）在（2）的条件下，抛物线上是否存在点P，使P A是⊙M的切线？若存在，求出P点的坐标，若不存在，说明理由．例3.如图，抛物线y＝ax2+bx+c（a，b，c是常数，a≠0）的对称轴为y轴，且经过（0，0）和（，）两点，点P在该抛物线上运动，以点P为圆心的⊙P总经过定点A（0，2）．（1）求a，b，c的值；（2）求证：在点P运动的过程中，⊙P始终与x轴相交；（3）设⊙P与x轴相交于M（x1，0），N（x2，0）（x1＜x2）两点，当△AMN 为等腰三角形时，求圆心P的纵坐标．练习9.已知：如图，抛物线y＝ax2+bx+1的图象关于y轴对称，且抛物线过点（2，2），点P为抛物线上的动点，以点P为圆心的⊙P与x轴相切，当点P运动对，⊙P始终经过y轴上的一个定点E．（1）求抛物线的解析式；（2）当⊙P的半径为时，⊙P与y轴交于M、N两点，求MN的长；（3）求定点E到直线y＝kx﹣8k的距离的最大值．练习10.已知：直线y＝﹣x﹣4分别交x、y轴于A、C两点，抛物线y＝ax2+bx （a＞0）经过A、O两点，且顶点B的纵坐标为﹣2（1）判断点B是否在直线AC上，并求该抛物线的函数关系式；（2）以点B关于x轴的对称点D为圆心，以OD为半径作⊙D，试判断直线AC与⊙D的位置关系，并说明理由；（3）若E为⊙D的优弧AO上一动点（不与A、O重合），连接AE、OE，问在抛物线上是否存在点P，使∠POA：∠AEO＝2：3？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．练习11.已知A是x轴正半轴上一个动点，以线段OA为直径作⊙B，圆心为点B，直径OA＝m，线段EF是⊙B的一条弦，EF∥x轴，点C为劣弧EF的中点，过点E作DE垂直于EF，交抛物线C1：y＝ax2+bx（a＞0）于点G，抛物线经过点O和点A．（1）求证：DG＝m；（2）拖动点A，如果抛物线C1与⊙B除点O和点A外有且只有一个交点，求b的值；（3）拖动点A，抛物线C1交⊙B于点O、E、F、A，①求证：DE＝m﹣；②直接写出FC2的值（用a，m的代数式表示）练习13.如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A．B两点，开口向下的抛物线经过点A，B，且其顶点P在⊙C上．（1）求∠ACB的大小；（2）写出A，B两点的坐标；（3）由圆与抛物线的对称性可知抛物线的顶点P的坐标为（1，3），求出抛物线的解析式；（4）在该抛物线上是否存在一点D点，使线段OP与CD互相平分？若存在，求出点D的坐标；若不存在，请说明理由．例4.如图1，抛物线y＝ax2+3ax（a为常数，a＜0）与x轴交于O，A两点，点B 为抛物线的顶点，点D是线段OA上的一个动点，连接BD并延长与过O，A，B三点的⊙P相交于点C，过点C作⊙P的切线交x轴于点E．（1）①求点A的坐标；②求证：CE＝DE；（2）如图2，连接AB，AC，BE，BO，当，∠CAE＝∠OBE时，①求证：AB2＝AC•BE；②求的值．练习14.如图1，已知圆O的圆心为原点，半径为2，与坐标轴交于A，C，D，E 四点，B为OD中点．（1）求过A，B，C三点的抛物线解析式；（2）如图2，连接BC，AC．点P在第一象限且为圆O上一动点，连接BP，交AC于点M，交OC于点N，当MC2＝MN•MB时，求M点的坐标；（3）如图3，若抛物线与圆O的另外两个交点分别为H，F，请判断四边形CFEH的形状，并说明理由．练习15.如图，二次函数与x轴的一个交点A的坐标为（﹣3，0），以点A为圆心作圆A，与该二次函数的图象相交于点B，C，点B，C的横坐标分别为﹣2，﹣5，连接AB，AC，并且满足AB⊥AC．过点B作BM⊥x轴于点M，过点C作CN⊥x轴于点N．（1）求该二次函数的关系式；（2）经过点B作直线BD，在A点右侧与x轴交于点D，与二次函数的图象交于点E，使得∠ADB＝∠ABM，连接AE，求证：AE＝AD；（3）若直线y＝kx+1与圆A相切，请求出k的值．例5.已知抛物线y＝ax2+bx+5（a≠0）经过A（5，0），B（6，1）两点，且与y 轴交于点C．（1）求抛物线y＝ax2+bx+5（a≠0）的函数关系式；（2）如图1，连接AC，E为线段AC上一点且横坐标为1，⊙P是△OAE外接圆，求圆心P点的坐标；（3）如图2，连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F；①点E在运动过程中四边形OEAF的面积是否为定值？如果是，请求出这个定值；如果不是，请说明理由；②求出当△AEF的面积取得最大值时，点E的坐标．练习16.如图1，已知抛物线y＝﹣x2+bx+c经过点A（1，0），B（﹣5，0）两点，且与y轴交于点C．（1）求b，c的值．（2）在第二象限的抛物线上，是否存在一点P，使得△PBC的面积最大？求出点P的坐标及△PBC的面积最大值．若不存在，请说明理由．（3）如图2，点E为线段BC上一个动点（不与B，C重合），经过B、E、O 三点的圆与过点B且垂直于BC的直线交于点F，当△OEF面积取得最小值时，求点E坐标．练习17.如图1，抛物线y＝+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C，顶点为D．（1）求抛物线的解析式；（2）如图2，以AB为直径在x轴上方画半圆交y轴于点E，圆心为G，P为半圆上一动点，连接DP，点Q为PD的中点．①判断点C、D与⊙G的位置关系，并说明原因；②当点P沿半圆从点B运动到点A时，求线段AQ的最小值．练习18.如图1，二次函数y＝ax2﹣3ax+b（a、b为参数，其中a＜0）的图象与x 轴交于A、B两点，与y轴交于点C，顶点为D．（1）若b＝﹣10a，求tan∠CBA的值（结果用含a的式子表示）；（2）若△ABC是等腰三角形，直线AD与y轴交于点P，且AP：DP＝2：3．求抛物线的解析式；（3）如图2，已知b＝﹣4a，E、F分别是CA和CB上的动点，且EF＝AB，若以EF为直径的圆经过点C，并交x轴于M、N两点，求MN的最大值．课后练习1.抛物线y＝ax2+bx﹣4交x轴于A（﹣2，0），B（4，0）两点，交y轴于点C，点P是介于B、C之间的抛物线上的动点（包括B、C两点），点E是△ABP 的外接圆圆心．（1）求抛物线的解析式；（2）如图1，当P为抛物线的顶点时，求圆心E的坐标；（3）如图2，作PH⊥x轴于点H，延长PH交⊙E于点Q，当P从C点出发，沿该抛物线运动到B点，求点Q在这个运动过程中的路径长．2.如图，在正方形OABC中，AB＝4，点E是线段OA（不含端点）边上一动点，作△ABE的外接圆交AC于点D．抛物线y＝ax2﹣x+c过点O，E．（1）求证：∠BDE＝90°；（2）如图1，若抛物线恰好经过点B，求此时点D的坐标；（3）如图2，AC与BE交于点F．①请问点E在运动的过程中，CF•AD是定值吗？如果是，请求出这个值，如果不是，请说明理由；②若，求点E坐标及a的值．。

【例1】.如图，点()40M ，，以点M 为圆心、2为半径的圆与x 轴交于点A B ，．已知抛物216y x bx c =++过点A 和B ，与y 轴交于点C ．⑴ 求点C 的坐标，并画出抛物线的大致图象．⑵ 点()8Q m ，在抛物线216y x bx c =++上，点P 为此抛物线对称轴上一个动点，求PQ PB + 最小值． ⑶ CE 是过点C 的M ⊙的切线，点E 是切点，求OE 所在直线的解析式．【巩固】已知抛物线2y ax bx c =++与y 轴的交点为C ，顶点为M ，直线CM 的解析式2y x =-+并且线段CM 的长为（1）求抛物线的解析式。

（2）设抛物线与x 轴有两个交点A （X 1 ，0）、B （X 2 ，0），且点A 在B 的左侧，求线段AB 的长。

（3）若以AB 为直径作⊙N ，请你判断直线CM 与⊙N 的位置关系，并说明理由。

【例2】如图，在平面直角坐标系中，以点(04)C ，为圆心，半径为4的圆交y 轴正半轴于点A ，AB 是C ⊙的切线．动点P 从点A 开始沿AB 方向以每秒1个单位长度的速度运动，点Q 从O 点开始沿x 轴正方向以每秒4个单位长度的速度运动，且动点P 、Q 从点A 和点O 同时出发，设运动时间为t (秒)．⑴当1t =时，得到1P 、1Q 两点，求经过A 、1P 、1Q 三点的抛物线解析式及对称轴l ；⑵当t 为何值时，直线PQ 与C ⊙相切？并写出此时点P 和点Q 的坐标；⑶在⑵的条件下，抛物线对称轴l 上存在一点N ，使NP NQ +最小，求出点N 的坐标并说明理由．提示：（1）先求出t=1时，AP 和OQ 的长，即可求得P 1，Q 1的坐标，然后用待定系数法即可得出抛物线的解析式．进而可求出对称轴l 的解析式．（2）当直线PQ 与圆C 相切时，连接CP ，CQ 则有Rt △CMP ∽Rt △QMC （M 为PG 与圆的切点），因此可设当t=a 秒时，PQ 与圆相切，然后用a 表示出AP ，OQ 的长即PM ，QM 的长（切线长定理）．由此可求出a 的值．（3）本题的关键是确定N 的位置，先找出与P 点关于直线l 对称的点P ′的坐标，连接P ′Q ，那么P ′Q 与直线l 的交点即为所求的N 点，可先求出直线P ′Q 的解析式，进而可求出N 点的坐标．【巩固】已知二次函数图象的顶点在原点O ，对称轴为y 轴．一次函数1y kx =+的图象与 二次函数的图象交于A B ，两点(A 在B 的左侧)，且A 点坐标为()44-，．平行于x 轴的直线l 过()01-，点．⑴ 求一次函数与二次函数的解析式；⑵ 判断以线段AB 为直径的圆与直线l 的位置关系，并给出证明；⑶ 把二次函数的图象向右平移2个单位，再向下平移t 个单位()0t >，二次函数的图象与x轴交于M N，，三点的圆的，两点，一次函数图象交y轴于F点．当t为何值时，过F M N面积最小？最小面积是多少？【例3】如图1,⊙O的半径为1，正方形ABCD顶点B坐标为()，，顶点D在⊙O上运动．50⑴当点D运动到与点A、O在同一条直线上时，试证明直线CD与⊙O相切；⑵当直线CD与⊙O相切时，求OD所在直线对应的函数关系式；⑶设点D的横坐标为x，正方形ABCD的面积为S，求S与x之间的函数关系式，并求出S 的最大值与最小值．【巩固】如图，已知点A 从()10，出发，以1个单位长度/秒的速度沿x 轴向正方向运动，以O A ，为顶点作菱形OABC ，使点B C ，在第一象限，且60AOC ∠=︒；以()03P ，为圆心，PC 为半径作圆．设点A 运动了t 秒，求： ⑴ 点C 的坐标（用含t 的代数式表示）；⑵ 当点A 在运动过程中，所有使P 与菱形OABC 的边所在直线相切的t 的值．【例4】已知：如图，抛物线213y x m =+与x 轴交于A B ，两点，与y 轴交于C 点，90ACB ∠=︒⑴ 求m 的值及抛物线顶点坐标；⑵ 过A B C ，，的三点的M ⊙交y 轴于另一点D ，连结DM 并延长交M ⊙于点E ，过E 点的M ⊙的切线分别交x 轴、y 轴于点F G ，，求直线FG 的解析式；⑶ 在条件⑵下，设P 为CBD 上的动点(P 不与C D ，重合)，连结PA 交y 轴于点H ，问是否存在一个常数k ，始终满足AH AP k ⋅=，如果存在，请写出求解过程；如果不存在，请说明理由．【巩固】如图，已知点A的坐标是()，，以AB为直径作O'，90-，，点B的坐标是()10交y轴的负半轴于点C，连接AC、BC，过A、B、C三点作抛物线．⑴求抛物线的解析式；⑵点E是AC延长线上一点，BCE∠的平分线CD交O'于点D，连结BD，求直线BD的解析式；⑶在⑵的条件下，抛物线上是否存在点P，使得PDB CBD∠=∠？如果存在，请求出点P的坐标；如果不存在，请说明理由．DCEA yxBO O'课后作业：1.如图，直角坐标系中，已知两点()A，，点B在第一象限且OAB2000O，，()∆为正三角形，OAB∆的外接圆交y轴的正半轴于点C，过点C的圆的切线交x轴于点D．⑴求B C，两点的坐标；⑵求直线CD的函数解析式；⑶设E F，分别是线段AB AD，上的两个动点，且EF平分四边形ABCD的周长．试探究：AEF∆的最大面积？参考答案例1【巩固】例2分析：（1）先求出t=1时，AP和OQ的长，即可求得P1，Q1的坐标，然后用待定系数法即可得出抛物线的解析式．进而可求出对称轴l的解析式．（2）当直线PQ与圆C相切时，连接CP，CQ则有Rt△CMP∽Rt△QMC（M为PG与圆的切点），因此可设当t=a秒时，PQ与圆相切，然后用a表示出AP，OQ的长即PM，QM的长（切线长定理）．由此可求出a的值．（3）本题的关键是确定N的位置，先找出与P点关于直线l对称的点P′的坐标，连接P′Q，那么P′Q与直线l的交点即为所求的N点，可先求出直线P′Q的解析式，进而可求出N点的坐标．【巩固】例3【巩固】例4【巩固】作业。

二次函数、圆综合检测题%1.选择题（共10小题每小题3分）1.对于二次函数y=- （x- 1） 2+2的图象与性质，下列说法正确的是（）A.对称轴是直线x=l,最小值是2B.对称轴是直线x=l,最大值是2C.对称轴是直线x=-l,最小值是2D.对称轴是直线x= - 1,最大值是22.己知二次函数y=ax2+bx+c （a^O）的图象如图所示，以下四个结论：①a>0；②c>0；（3）b2 - 4ac>0；④- Evo,正确的是（）2aA.①②B.②④C.①③D.③④3.若抛物线y= - x2+bx+c经过点（-2, 3）,则2c - 4b - 9的值是（）/A. 5B. - 1C. 4 .D. 184 .如图将半径为2cm的圆形纸片折叠后，痕AB 的长为（）A. 2cm B. /cm5.如图，。

中，弦AB、CD相交于点P,的大小是（）A. 43° B. 35° C. 34°6.AB是。

的直径，PA切。

0于点A, P0交。

0于点C；连接BC,若ZP=40°,则匕B等于（）A. 20°B. 25°C. 30°D. 40°7.如图，。

是ZiABC的外接圆，BC=2, ZBAC=30°,则劣弧而的圆弧恰好经过圆心0,则折长等于（）A尧容•斗”写8.如图，在Rt^ABC 中，ZBCA=90°, ZBAC=30°, BC=2,将RtAABC 绕A点顺时针旋转90。

得到RtAADE,则BC扫过的面积为（）A. —B. （2-如）nC.空邕D. R2 29.如图，抛物线y=ax2+bx+c （a乂0）的对称轴为直线x=l,与x轴的一个交点.坐标为（-1, 0）,其部分图象如图所示，下列结论：①4ac<b2；②方程ax2+bx+c=0的两个根是Xi= - 1, X?二3；③3a+c>0④当y>OI3寸，x的取值范围是- 1W X V3⑤当x<0时，y随x增大而增大其中结论正确的个数是（）A. 4个B. 3个C・2个D・1个10.如图，在Z^ABC 中，匕090°, AB=10cm, BC=8cm,点P 从点A 沿AC 向点C 以lcm/s的速度运动，同时点Q从点C沿CB向点B以2cm/s的速度运动（点Q运动到点B停止）, 在运动过程中，四边形PABQ的面积最小值为（A. 19cm2B. 16cm2C. 15cm2D. 12cm2%1.填空题（共5小题，每小题4分）11.已知一个二次函数的图象开口向上，顶点坐标为（0, - 1 ）,那么这个二次函数的解析式可以是.（只需写一个）12.已知。

二次函数与圆的综合题3例1、抛物线2y ax bx c =++交x 轴于A 、B 两点，交y 轴于点C ,已知抛物线的对称轴为1x =，(3,0)B ,(0,3)C -， ⑴求二次函数2y ax bx c =++的解析式；⑵在抛物线对称轴上是否存在一点P ，使点P 到B 、C 两点距离之差最大？若存在，求出P 点坐标；若不存在，请说明理由； ⑶平行于x 轴的一条直线交抛物线于M N 、两点，若以MN 为直径的圆恰好与x 轴相切，求此圆的半径．解：（1）将(0,3)C - (3,0)B 代入c bx ax y ++=2，．∵1x =是对称轴， 322--=x x y ．（2）AC 与对称轴的交点P 即为到B C 、的距离之差最大的点．∵C 点的坐标为(0,3)-，A 点的坐标为(1,0)-，∴ 直线AC 的解析式是33--=x y ，又对称轴为1x =，∴ 点P 的坐标(1,6)-． （3）设1(,)M x y 、2(,)N x y ，所求圆的半径为r ，则 r x x 212=-，.(1) ∵对称轴为1x =，∴ 212=+x x ． .(2)由（1）、（2）得：12+=r x ．.(3) 将(1,)N r y +代入解析式322--=x x y ，得 3)1(2)1(2-+-+=r r y ，.(4)整理得： 42-=r y ．由于 r=±y ，当0>y 时，042=--r r ，解得，21711+=r ， 21712-=r （舍去），当0<y 时，042=-+r r ，解得，21711+-=r ， 21712--=r （舍去）．所以圆的半径是2171+或2171+-． 练习：⊙O 半径为2，弦BD ＝32，A 为弧BD 的中点，E 为弦AC 的中点，且在BD 上。

求：四边形ABCD 的面积。

解：连结OA 、OB ，OA 交BD 于F 。

⎭⎬⎫===⊥⇒2 3,BD A OB FD BF BD OF 的中点为弧 1AF 1OF =⇒=⇒3AF BD 21S ABD =⋅=⇒∆ CBE ABE CDE ADE S S S S CE AE ∆∆∆∆==⇒=，322S S ABD ABCD ==⇒∆四边形B O DA例2、已知一次函数y=kx-4k 的图象与x 轴交于点A ，抛物线y ax bx c =++2经过O 、A 两点。

例题精讲【例1】．如图，抛物线的顶点为A（0，2），且经过点B（2，0）．以坐标原点O为圆心的圆的半径r＝，OC⊥AB于点C．（1）求抛物线的函数解析式．（2）求证：直线AB与⊙O相切．（3）已知P为抛物线上一动点，线段PO交⊙O于点M．当以M，O，A，C为顶点的四边形是平行四边形时，求PM的长．解：（1）∵抛物线的顶点为A（0，2），∴可设抛物线的解析式为：y＝ax2+2，∵抛物线经过点B（2，0），∴4a+2＝0，解得：a＝﹣，∴抛物线的解析式为：y＝﹣x2+2；（2）证明：∵A（0，2），B（2，0），∴OA＝OB＝2，∴AB＝2，∵OC⊥AB，∴•OA•OB＝•AB•OC，∴×2×2＝×2•OC，解得：OC＝，∵⊙O的半径r＝，∴OC是⊙O的半径，∴直线AB与⊙O相切；（3）∵点P在抛物线y＝﹣x2+2上，∴可设P（x，﹣x2+2），以M，O，A，C为顶点的四边形是平行四边形时，可得：AC＝OM＝，CM＝OA＝2，∵点C是AB的中点，∴C（1，1），M（1，﹣1），设直线OM的解析式为y＝kx，将点M（1，﹣1）代入，得：k＝﹣1，∴直线OM的解析式为y＝﹣x，∵点P在OM上，∴﹣x2+2＝﹣x，解得：x1＝1+，x2＝1﹣，∴y1＝﹣1﹣，y2＝﹣1+，∴P1（1+，﹣1﹣），P2（1﹣，﹣1+），如图，当点P位于P1位置时，OP1＝＝＝（1+）＝+，∴P1M＝OP1﹣OM＝+﹣＝，当点P位于P2位置时，同理可得：OP2＝﹣，∴P2M＝OP2﹣OM＝﹣﹣＝﹣2；综上所述，PM的长是或﹣2．变式训练【变1-1】．如图，抛物线y＝ax2+bx+2与直线AB相交于A（﹣1，0），B（3，2），与x轴交于另一点C．（1）求抛物线的解析式；（2）在y上是否存在一点E，使四边形ABCE为矩形，若存在，请求出点E的坐标；若不存在，请说明理由；（3）以C为圆心，1为半径作⊙O，D为⊙O上一动点，求DA+DB的最小值解：（1）把A（﹣1，0）、B（3，2）代入y＝ax2+bx+2，得，解得，∴抛物线的解析式为y＝x2+x+2．（2）存在．如图1，作AE⊥AB交y轴于点E，连结CE；作BF⊥x轴于点F，则F（3，0）．当y＝0时，由x2+x+2＝0，得x1＝1，x2＝4，∴C（4，0），∴CF＝AO＝1，AF＝3﹣（﹣1）＝4；又∵BF＝2，∴，∵∠BFC＝∠AFB＝90°，∴△BFC∽△AFB，∴∠CBF＝∠BAF，∴∠ABC＝∠CBF+∠ABF＝∠BAF+∠ABF＝90°，∴BC∥AE，∵∠BCF＝90°﹣∠BAC＝∠EAO，∠BFC＝∠EOA＝90°，∴△BCF≌△EAO（ASA），∴BC＝EA，∴四边形ABCE是矩形；∵OE＝FB＝2，∴E（0，﹣2）．（3）如图2，作FL⊥BC于点L，连结AL、CD.由（2）得∠BFC＝90°，BF＝2，CF＝1，∴CF＝CD，CB＝＝．∵∠FLC＝∠BFC＝90°，∠FCL＝∠BCF（公共角），∴△FCL∽△BCF，∴＝，∴＝，∵∠DCL＝∠BCD（公共角），∴△DCL∽△BCD，∴＝，∴LD＝DB；∵DA+LD≥AL，∴当DA+LD＝AL，即点D落在线段AL上时，DA+DB＝DA+LD＝AL最小．∵CL＝CF＝，∴BL＝＝，∴BL2＝（）2＝，又∵AB2＝22+42＝20，∴AL＝＝＝，DA+DB的最小值为．【例2】．如图1，在平面直角坐标系中，抛物线与x轴分别交于A、B两点，与y轴交于点C（0，6），抛物线的顶点坐标为E（2，8），连结BC、BE、CE．（1）求抛物线的表达式；（2）判断△BCE的形状，并说明理由；（3）如图2，以C为圆心，为半径作⊙C，在⊙C上是否存在点P，使得BP+EP 的值最小，若存在，请求出最小值；若不存在，请说明理由．解：（1）∵抛物线的顶点坐标为E（2，8），∴设该抛物线的表达式为y＝a（x﹣2）2+8，∵与y轴交于点C（0，6），∴把点C（0，6）代入得：a＝﹣，∴该抛物线的表达式为y＝x2+2x+6；（2）△BCE是直角三角形．理由如下：∵抛物线与x轴分别交于A、B两点，∴令y＝0，则﹣（x﹣2）2+8＝0，解得：x1＝﹣2，x2＝6，∴A（﹣2，0），B（6，0），∴BC2＝62+62＝72，CE2＝（8﹣6）2+22＝8，BE2＝（6﹣2）2+82＝80，∴BE2＝BC2+CE2，∴∠BCE＝90°，∴△BCE是直角三角形；（3）⊙C上存在点P，使得BP+EP的值最小且这个最小值为．理由如下：如图，在CE上截取CF＝（即CF等于半径的一半），连结BF交⊙C于点P，连结EP，则BF的长即为所求．理由如下：连结CP，∵CP为半径，∴＝＝，又∵∠FCP＝∠PCE，∴△FCP∽△PCE，∴＝＝，即FP＝EP，∴BF＝BP+EP，由“两点之间，线段最短”可得：BF的长即BP+EP为最小值．∵CF＝CE，E（2，8），∴由比例性质，易得F（，），∴BF＝＝．变式训练【变2-1】．在平面直角坐标系中，二次函数y＝x2+bx+c的图象与x轴交于A（﹣2，0），B（4，0）两点，交y轴于点C，点P是第四象限内抛物线上的一个动点．（1）求二次函数的解析式；（2）如图甲，当△ACP是以AC为直角边的直角三角形时，求点P的坐标；（3）如图乙，过A，B，P三点作⊙M，过点P作PE⊥x轴，垂足为D．交OM于点E．点P在运动过程中线段DE的长是否变化，若有变化，求出DE的取值范围；若不变，求DE的长．解：（1）把A（﹣2，0），B（4，0）代入y＝x2+bx+c得：，解得，∴二次函数的解析式为y＝x2﹣x﹣4；（2）如图：由y＝x2﹣x﹣4可得C（0，﹣4），设P（x，x2﹣x﹣4），∴AC2＝（﹣2﹣0）2+（0+4）2＝20，CP2＝x2+（x2﹣x）2，AP2＝（x+2）2+（x2﹣x ﹣4）2，∵△ACP是以AC为直角边的直角三角形，∴AC2+CP2＝AP2，即20+x2+（x2﹣x）2＝（x+2）2+（x2﹣x﹣4）2，∴20+x2+（x2﹣x）2＝x2+4x+4+（x2﹣x）2﹣8（x2﹣x）+16，解得x＝0（与C重合，舍去）或x＝3，∴P（3，﹣）；（3）点P在运动过程中线段DE的长不变，理由如下：连接AP、BE，如图：∵＝，＝，∴∠APD＝∠DBE，∠DAP＝∠DEB，∴△ADP∽△EDB，∴＝，∴DE＝，设P（m，m2﹣m﹣4），则D（m，0），∵A（﹣2，0），B（4，0），C（0，﹣4），∴AD＝m+2，BD＝4﹣m，PD＝﹣（m2﹣m﹣4）＝﹣m2+m+4，∴DE＝＝＝2，∴DE是定值2，∴点P在运动过程中线段DE的长不变，是定值2．1．如图，已知⊙P的半径为2，圆心P在抛物线y＝x2﹣1上运动，当⊙P与坐标轴相切时，圆心P的坐标可以是（，2）或（﹣，2）或（2，1）或（﹣2，1）．解：分两种情况：（1）当⊙P与x轴相切时，依题意，可设P（x，2）或P（x，﹣2）．①当P的坐标是（x，2）时，将其代入y＝x2﹣1，得2＝x2﹣1，解得x＝±，此时P（，2）或（﹣，2）；②当P的坐标是（x，﹣2）时，将其代入y＝x2﹣1，得﹣2＝x2﹣1，无解．（2）当⊙P与y轴相切时，∵⊙P的半径为2，∴当⊙P与y轴相切时，点P到y轴的距离为2，∴P点的横坐标为2或﹣2，当x＝2时，代入y＝x2﹣1可得y＝1，当x＝﹣2时，代入y＝x2﹣1可得y＝1，∴点P的坐标为（2，1）或（﹣2，1），综上所述，符合条件的点P的坐标是（，2）或（﹣，2）或（2，1）或（﹣2，1）；故答案为：（，2）或（﹣，2）或（2，1）或（﹣2，1）．2．如图1，抛物线与x轴交于O、A两点，点B为抛物线的顶点，连接OB．（1）求∠AOB的度数；（2）如图2，以点A为圆心，4为半径作⊙A，点M在⊙A上．连接OM、BM，①当△OBM是以OB为底的等腰三角形时，求点M的坐标；②如图3，取OM的中点N，连接BN，当点M在⊙A上运动时，求线段BN长度的取值范围．解：（1）令y＝0，则﹣2x＝0，解得：x＝0或8．∴A（8，0）．∴OA＝8．∵y＝﹣2x＝﹣4，∴B（4，﹣4）．过点B作BD⊥OA于点D，如图，则OD＝4，BD＝4，∴OD＝BD，∴∠AOB＝∠OBD＝45°；（2）①设⊙A与x轴交于点C，则C（4，0）．连接BC，如图，∵B（4，﹣4），∴BC⊥OA．∵CO＝CB＝4，∴△CBO是以OB为底的等腰三角形．∴点M与点C重合时，△MBO是以OB为底的等腰三角形．此时点M（4，0）；过点A作AM⊥x轴，交⊙A于点M，延长MA交⊙A于点E，连接BE，过点M作MF⊥y轴于点F，如图，则M（8，4），E（8，﹣4），F（，4）．∴MF＝ME＝8．∵B（4，﹣4），∴BE∥x轴．∴BE⊥ME，BE＝4．∴∠BEM＝∠MFO＝90°，BE＝OF＝4．在△MOF和△MBE中，，∴△MOF≌△MBE（SAS）．∴MO＝MB．∴△MBO是以OB为底的等腰三角形．此时点M（8，4）；综上，当△OBM是以OB为底的等腰三角形时，点M的坐标为（4，0）或（8，4）；②设⊙A与x轴交于点C，则C（4，0）．连接BC，CN，AM，如图，∵A（8，0），∴点C是OA的中点．∵N为OM的中点，∴CN是△OMA的中位线．∴CN＝AM＝2．当点M在⊙A上运动时，由三角形的三边的关系定理可知：BC﹣CN≤BN≤BC+CN．∵BC＝4，∴4﹣2≤BN≤4+2．∴线段BN长度的取值范围为：2≤BN≤6．3．如图，抛物线y＝ax2﹣2ax﹣3a（a＞0）与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，且OB＝OC．（1）求抛物线的解析式；（2）如图1，若点P是线段BC（不与B，C重合）上一动点，过点P作x轴的垂线交抛物线于M点，连接CM，将△PCM沿CM对折，如果点P的对应点N恰好落在y轴上，求此时点P的坐标；（3）如图2，若第四象限有一动点E，满足BE＝OB，过E作EF⊥x轴于点F，设F坐标为（t，0），0＜t＜3，△BEF的内心为I，连接CI，直接写出CI的最小值．解：（1）在y＝ax2﹣2ax﹣3a（a＞0）中，令y＝0，得：ax2﹣2ax﹣3a＝0，解得：x1＝3，x2＝﹣1，∴A（﹣1，0），B（3，0），∴OB＝3，∵OB＝OC，∴OC＝3，∴C（0，﹣3），∴﹣3a＝﹣3，∴a＝1，∴抛物线解析式为：y＝x2﹣2x﹣3．（2）设直线BC解析式为y＝kx+b，∵B（3，0），C（0，﹣3），∴，解得：，∴直线BC解析式为：y＝x﹣3，设M点坐标为（m，m2﹣2m﹣3），∵PM⊥x轴，∴P（m，m﹣3），∴PM＝m﹣3﹣（m2﹣2m﹣3）＝﹣m2+3m，∵OB＝OC，∠BOC＝90°，∴CB＝OB，∴CP＝m，∵△PCM沿CM对折，点P的对应点N恰好落在y轴上，∴∠PCM＝∠NCM，∵PM∥y轴，∴∠NCM＝∠PMC，∴∠PCM＝∠PMC，∴PC＝PM，∴m＝﹣m2+3m，整理得：m2+（﹣3）m＝0，解得：m1＝0（舍去），m2＝3﹣，∴当m＝3﹣时，m﹣3＝﹣，∴P（3﹣，﹣）．（3）如图2，连接BI，OI，EI，作△OBI的外接圆⊙M，连接OM，BM，MI，CM，过M作MH⊥y轴于H，∵EF⊥x轴，∴∠BFE＝90°，∴∠FBE+∠FEB＝90°，∵△BEF的内心为I，∴BI，EI分别平分∠FBE，∠FEB，∴∠IBE＝∠FBE，∠IEB＝∠FEB，∴∠IBE+∠IEB＝（∠FBE+∠FEB）＝45°，∴∠BIE＝135°，在△BIO和△BIE中，，∴△BIO≌△BIE（SAS），∴∠BIO＝∠BIE＝135°，∵⊙M是△OBI的外接圆，∴∠OMB＝2×（180°﹣∠BIO）＝90°，∴OM＝BM＝OB＝，∴MI＝OM＝，∴∠MOB＝∠MOH＝45°，∵MH⊥y轴，∴∠HOM＝∠HMO＝45°，∴OH＝HM＝OM＝，∴CH＝OH+OC＝+3＝，∴CM＝＝，∵CI≥CM﹣MI，当且仅当C、M、I三点共线时，CI取得最小值，∴CI的最小值为﹣．4．已知抛物线y＝x2﹣（2m﹣1）x+4m﹣6．（1）试说明对于每一个实数m，抛物线都经过x轴上的一个定点；（2）设抛物线与x轴的两个交点A（x1，0）和B（x2，0）（x1＜x2）分别在原点的两侧，且A、B两点间的距离小于6，求m的取值范围；（3）抛物线的对称轴与x轴交于点C，在（2）的条件下，试判断是否存在m的值，使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D，且被x轴截得的劣弧与是等弧？若存在，求出所有满足条件的m的值；若不存在，说明理由．解：（1）由题意可知：y＝（x﹣2）（x﹣2m+3），因此抛物线与x轴的两个交点坐标为：（2，0）（2m﹣3，0），因此无论m取何值，抛物线总与x轴交于（2，0）点；（2）令y＝0，有：x2﹣（2m﹣1）x+4m﹣6＝0，则：x1+x2＝2m﹣1，x1x2＝4m﹣6；∵AB＜6∴x2﹣x1＜6，即（x2﹣x1）2＜36，（x1+x2）2﹣4x1x2＜36，即（2m﹣1）2﹣4（4m﹣6）＜36，解得﹣＜x＜．①根据A、B分别在原点两侧可知：x1x2＜0，即4m﹣6＜0，m＜．②综合①②可得﹣＜m＜；（3）假设存在这样的m，设圆M与y轴的切点为D，过M作x轴的垂线设垂足为E．①当C点在x轴正半轴时，x＝＞0，因此＜m＜，∵弧BC＝弧CD，因此BC＝CD．OC＝，CD＝BC＝OB﹣OC＝2﹣＝，EC＝BC＝，OE＝MD＝OC+CE＝+＝．易知：OD＝ME，即OD2＝ME2∴CD2﹣OC2＝CM2﹣CE2，（）2﹣（）2＝（）2﹣（）2；解得m＝，符合m的取值范围．②当C点在x轴负半轴时，x＝＜0，因此﹣＜m＜，同①可求得OC＝，CD＝AC＝，CE＝，MD＝OE＝．同理有：CD2﹣OC2＝MC2﹣CE2（）2﹣（）2＝（）2﹣（）2化简得：m2＝，∴m＝±，均不符合m的取值范围，因此这种情况不成立．综上所述，存在符合条件的m，且m＝．5．已知抛物线y＝x2+mx﹣2m﹣4（m＞0）．（1）证明：该抛物线与x轴总有两个不同的交点；（2）设该抛物线与x轴的两个交点分别为A，B（点A在点B的右侧），与y轴交于点C，A，B，C三点都在⊙P上．①试判断：不论m取任何正数，⊙P是否经过y轴上某个定点？若是，求出该定点的坐标；若不是，说明理由；②若点C关于直线x＝﹣的对称点为点E，点D（0，1），连接BE，BD，DE，△BDE的周长记为l，⊙P的半径记为r，求的值．解：（1）令y＝0，∴x2+mx﹣2m﹣4＝0，∴△＝m2﹣4[﹣2m﹣4]＝m2+8m+16，∵m＞0，∴Δ＞0，∴该抛物线与x轴总有两个不同的交点；（2）令y＝0，∴x2+mx﹣2m﹣4＝0，∴（x﹣2）[x+（m+2）]＝0，∴x＝2或x＝﹣（m+2），∴A（2，0），B（﹣（m+2），0），∴OA＝2，OB＝m+2，令x＝0，∴y＝﹣2（m+2），∴C（0，﹣2（m+2）），∴OC＝2（m+2），①通过定点（0，1）理由：如图，∵点A，B，C在⊙P上，∴∠OCB＝∠OAF，在Rt△BOC中，tan∠OCB＝＝＝，在Rt△AOF中，tan∠OAF＝＝＝，∴OF＝1，∴点F的坐标为（0，1）；②如图1，由①知，点F（0，1），∵D（0，1），∴点D在⊙P上，∵点E是点C关于抛物线的对称轴的对称点，∴∠DCE＝90°，∵⊙P是△ABC的外接圆，∴点P在抛物线的对称轴上，∴点E在⊙P上，∴DE是⊙P的直径，∴∠DBE＝90°，∵∠BED＝∠OCB，∴tan∠BED＝，设BD＝n，在Rt△BDE中，tan∠BED＝＝＝，∴BE＝2n，根据勾股定理得，DE＝＝n，∴l＝BD+BE+DE＝（3+）n，r＝DE＝n，∴＝＝．6．如图所示，在平面直角坐标系中，⊙C经过坐标原点O，且与x轴，y轴分别相交于M （4，0），N（0，3）两点．已知抛物线开口向上，与⊙C交于N，H，P三点，P为抛物线的顶点，抛物线的对称轴经过点C且垂直x轴于点D．（1）求线段CD的长及顶点P的坐标；（2）求抛物线的函数表达式；＝8S△QAB，（3）设抛物线交x轴于A，B两点，在抛物线上是否存在点Q，使得S四边形OPMN 且△QAB∽△OBN成立？若存在，请求出Q点的坐标；若不存在，请说明理由．解：（1）如图，连接OC，∵M（4，0），N（0，3），∴OM＝4，ON＝3，∴MN＝5，∴OC＝MN＝，∵CD为抛物线对称轴，∴OD＝MD＝2，在Rt△OCD中，由勾股定理可得CD＝＝＝，∴PD＝PC﹣CD＝﹣＝1，∴P（2，﹣1）；（2）∵抛物线的顶点为P（2，﹣1），∴设抛物线的函数表达式为y＝a（x﹣2）2﹣1，∵抛物线过N（0，3），∴3＝a（0﹣2）2﹣1，解得a＝1，∴抛物线的函数表达式为y＝（x﹣2）2﹣1，即y＝x2﹣4x+3；（3）在y＝x2﹣4x+3中，令y＝0可得0＝x2﹣4x+3，解得x＝1或x＝3，∴A（1，0），B（3，0），∴AB＝3﹣1＝2，∵ON＝3，OM＝4，PD＝1，＝S△OMP+S△OMN＝OM•PD+OM•ON＝×4×1+×4×3＝8＝8S△QAB，∴S四边形OPMN＝1，∴S△QAB设Q点纵坐标为y，则×2×|y|＝1，解得y＝1或y＝﹣1，当y＝1时，则△QAB为钝角三角形，而△OBN为直角三角形，不合题意，舍去，当y＝﹣1时，可知P点即为所求的Q点，∵D为AB的中点，∴AD＝BD＝QD，∴△QAB为等腰直角三角形，∵ON＝OB＝3，∴△OBN为等腰直角三角形，∴△QAB∽△OBN，综上可知存在满足条件的点Q，其坐标为（2，﹣1）．7．如图，已知二次函数的图象顶点在原点，且点（2，1）在二次函数的图象上，过点F（0，1）作x轴的平行线交二次函数的图象于M、N两点．（1）求二次函数的表达式；（2）P为平面内一点，当△PMN是等边三角形时，求点P的坐标；（3）在二次函数的图象上是否存在一点E，使得以点E为圆心的圆过点F和点N，且与直线y＝﹣1相切．若存在，求出点E的坐标，并求⊙E的半径；若不存在，说明理由．解：（1）∵二次函数的图象顶点在原点，故设二次函数表达式为：y＝ax2，将（2，1）代入上式并解得：a＝，故二次函数表达式为：y＝x2；（2）将y＝1代入y＝x2并解得：x＝±2，故点M、N的坐标分别为（﹣2，1）、（2，1），则MN＝4，∵△PMN是等边三角形，∴点P在y轴上且PM＝4，∴PF＝2；∵点F（0，1），∴点P的坐标为（0，1+2）或（0，1﹣2）；（3）假设二次函数的图象上存在一点E满足条件，设点Q是FN的中点，则点Q（1，1），故点E在FN的中垂线上．∴点E是FN的中垂线与y＝x2图象的交点，∴y＝×12＝，则点E（1，），EN＝＝，同理EF＝＝，点E到直线y＝﹣1的距离为|﹣（﹣1）|＝，故存在点E，使得以点E为圆心半径为的圆过点F，N且与直线y＝﹣1相切．8．已知二次函数y＝﹣x2+bx+c+1，①当b＝1时，求这个二次函数的对称轴的方程；②若c＝﹣b2﹣2b，问：b为何值时，二次函数的图象与x轴相切？③若二次函数的图象与x轴交于点A（x1，0），B（x2，0），且x1＜x2，b＞0，与y轴的正半轴交于点M，以AB为直径的半圆恰好过点M，二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F，且满足＝，求二次函数的表达式．解：①二次函数y＝﹣x2+bx+c+1的对称轴为x＝，当b＝1时，＝，∴当b＝1时，求这个二次函数的对称轴的方程为x＝．②二次函数y＝﹣x2+bx+c+1的顶点坐标为（，），∵二次函数的图象与x轴相切且c＝﹣b2﹣2b，∴，解得：b＝，∴b为，二次函数的图象与x轴相切．③∵AB是半圆的直径，∴∠AMB＝90°，∴∠OAM+∠OBM＝90°，∵∠AOM＝∠MOB＝90°，∴∠OAM+∠OMA＝90°，∴∠OMA＝∠OBM，∴△OAM∽△OMB，∴，∴OM2＝OA•OB，∵二次函数的图象与x轴交于点A（x1，0），B（x2，0），∴OA＝﹣x1，OB＝x2，x1+x2，＝b，x1•x2＝﹣（c+1），∵OM＝c+1，∴（c+1）2＝c+1，解得：c＝0或c＝﹣1（舍去），∴c＝0，OM＝1，∵二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F，且满足＝，∴AD＝BD，DF＝4DE，DF∥OM，∴△BDE∽△BOM，△AOM∽△ADF，∴，，∴DE＝，DF＝，∴×4，∴OB＝4OA，即x2＝﹣4x1，∵x1•x2＝﹣（c+1）＝﹣1，∴，解得：，∴b＝﹣+2＝，∴二次函数的表达式为y＝﹣x2+x+1．9．已知抛物线y＝ax2+bx+c过点A（0，2）．若该抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足；当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为圆心，OA为半径的圆与抛物线的另两个交点为B，C，且△ABC 有一个内角为60°．①求抛物线的解析式；②若点P与点O关于点A对称，且O，M，N三点共线，求证：PA平分∠MPN．解：①当x1＜x2＜0时，x1﹣x2＜0，∵（x1﹣x2）（y1﹣y2）＞0，∴y1﹣y2＜0，∴当x＜0时，y随x的增大而增大，当0＜x1＜x2时，x1﹣x2＜0，∵（x1﹣x2）（y1﹣y2）＜0，∴y1﹣y2＞0，∴当x＞0时，y随x的增大而减小．∴抛物线关于y轴对称，∴b＝0，∵抛物线y＝ax2+bx+c过点A（0，2），∴c＝2，如图，连接OB、OC，设BC y轴于点D．由对称性可知，△ABC为等腰三角形，又∵△ABC有一个内角为60°，∴△ABC是等边三角形，∴OD＝OA＝1，CD＝OD＝，∴B（﹣，﹣1），C（，﹣1），将C点坐标代入y＝ax2+2可求得a＝﹣1，∴抛物线的解析式为y＝﹣x2+2．②设直线OM的解析式为y＝k1x，∵O、M、N三点共线，∴x1≠0，x2≠0，且＝，化为x1﹣x2＝，∵x1≠x2，∴x1x2＝﹣2，∴，∴，设点N关于y轴的对称点为N'，则N'的坐标为，∵点P是点O关于点A的对称点，∴OP﹣2OA＝4，即点P的坐标为（0，4），设直线PM的解析式为y＝k2x+4，∵点M的坐标为，∴，∴，∴直线PM的解析式为x+4．∵，即N'在直线PM上，∴PA平分∠MPN．10．如图，在平面直角坐标系xOy中，O为坐标原点，点A（4，0），点B（0，4），△ABO 的中线AC与y轴交于点C，且⊙M经过O，A，C三点．（1）求圆心M的坐标；（2）若直线AD与⊙M相切于点A，交y轴于点D，求直线AD的函数表达式；（3）在（2）的条件下，在过点B且以圆心M为顶点的抛物线上有一动点P，过点P作PE∥y轴，交直线AD于点E．若以PE为半径的⊙P与直线AD相交于另一点F．当EF ＝4时，求点P的坐标．解：（1）点B（0，4），则点C（0，2），∵点A（4，0），则点M（2，1）；（2）应该是圆M与直线AD相切，则∠CAD＝90°，设：∠CAO＝α，则∠CAO＝∠ODA＝∠PEH＝α，tan∠CAO＝＝＝tanα，则sinα＝，cosα＝，AC＝，则CD＝＝10，则点D（0，﹣8），将点A、D的坐标代入一次函数表达式：y＝mx+n并解得：直线AD的表达式为：y＝2x﹣8；（3）抛物线的表达式为：y＝a（x﹣2）2+1，将点B坐标代入上式并解得：a＝，故抛物线的表达式为：y＝x2﹣3x+4，过点P作PH⊥EF，则EH＝EF＝2，cos∠PEH＝，解得：PE＝5，设点P（x，x2﹣3x+4），则点E（x，2x﹣8），则PE＝x2﹣3x+4﹣2x+8＝5，解得x＝或2，则点P（，）或（2，1）．11．如图，抛物线y＝ax2+6ax（a为常数，a＞0）与x轴交于O，A两点，点B为抛物线的顶点，点D的坐标为（t，0）（﹣3＜t＜0），连接BD并延长与过O，A，B三点的⊙P相交于点C．（1）求点A的坐标；（2）过点C作⊙P的切线CE交x轴于点E．①如图1，求证：CE＝DE；②如图2，连接AC，BE，BO，当a＝，∠CAE＝∠OBE时，求﹣的值．解：（1）令ax2+6ax＝0，ax（x+6）＝0，∴A（﹣6，0）；（2）①证明：如图，连接PC，连接PB，延长交x轴于点M，∵⊙P过O、A、B三点，B为顶点，∴PM⊥OA，∠PBC+∠BDM＝90°，又∵PC＝PB，∴∠PCB＝∠PBC，∵CE为切线，∴∠PCB+∠ECD＝90°，又∵∠BDM＝∠CDE，∴∠ECD＝∠CDE，∴CE＝DE．②解：设OE＝m，点D的坐标为（t，0），∵∠CAE＝∠CBO，∠CAE＝∠OBE，∴∠CBO＝∠EBO，由角平分线成比例定理可得：，即：，∴，∴，∴，＝，＝．12．抛物线y＝﹣x2+x﹣1与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，其顶点为D．将抛物线位于直线l：y＝t（t＜）上方的部分沿直线l向下翻折，抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象．（1）点B，D的坐标分别为（3，0），（，）；（2）如图①，抛物线翻折后，点D落在点E处，当点E在△ABC内（含边界）时，求t的取值范围；（3）如图②，当t＝0时，点Q是“M”形新图象上一动点．①直接写出“M”形图象AB段的函数关系式；②是否存在以CQ为直径的圆与x轴相切于点P？若存在，求出点P的坐标；若不存在，请说明理由．解：（1）令y＝0，则﹣x2+x﹣1＝0，解得x＝3或x＝，∴B（3，0），A（，0），令x＝0，则y＝﹣1，∴C（0，﹣1），∵y＝﹣x2+x﹣1＝﹣（x﹣）2+，∴顶点D（，），故答案为：（3，0），（，）；（2）∵E与D关于直线y＝t对称，∴E（，2t﹣），设直线BC的解析式为y＝kx+b，将B（3，0），C（0，﹣1）代入，得，∴，∴y＝x﹣1，当x＝时，y＝﹣，∵E点在△ABC内（含边界），∴2t﹣≥﹣，∴t≥，∵2t﹣≤0，∴t≤，∵t＜，∴t的取值范围是≤t≤；（3）①当t＝0时，y＝﹣x2+x﹣1关于x轴对称的函数为y＝x2﹣x+1，∴“M”形图象AB段的函数关系式为y＝x2﹣x+1（≤x≤3）；②存在点P，理由如下：设Q点的横坐标为m，∵以CQ为直径的圆与x轴相切于点P，∴P点的横坐标为m，当m＞3或m＜时，Q（m，﹣m2+m﹣1），∵△CPQ为直角三角形，∴CQ2＝CP2+PQ2，即m2+（﹣m2+m）2＝m2+1+m2+（﹣m2+m﹣1）2，解得m＝或m＝，∴P（，0）或P（，0）；当≤m≤3时，Q（m，m2﹣m+1），∵△CPQ为直角三角形，∴CQ2＝CP2+PQ2，即m2+（m2﹣m+2）2＝m2+1+m2+（m2﹣m+1）2，解得m＝2或m＝，∴P（，0）或P（1，0）；综上所述：存在以CQ为直径的圆与x轴相切于点P，P点坐标为（，0）或（，0）或（，0）或P（1，0）．13．已知抛物线y＝ax2+bx+c过点A（0，2）．（1）若点（﹣，0）也在该抛物线上，求a，b满足的关系式；（2）若该抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为心，OA为半径的圆与抛物线的另两个交点为B，C，且△ABC有一个内角为60°．①求抛物线的解析式；②若点P与点O关于点A对称，且O，M，N三点共线，求证：PA平分∠MPN．解：（1）∵抛物线y＝ax2+bx+c过点A（0，2），∴c＝2．又∵点（﹣，0）也在该抛物线上，∴a（﹣）2+b（﹣）+c＝0，∴2a﹣b+2＝0（a≠0）．（2）①∵当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0，∴x1﹣x2＜0，y1﹣y2＜0，∴当x＜0时，y随x的增大而增大；同理：当x＞0时，y随x的增大而减小，∴抛物线的对称轴为y轴，开口向下，∴b＝0．∵OA为半径的圆与抛物线的另两个交点为B、C，∴△ABC为等腰三角形，又∵△ABC有一个内角为60°，∴△ABC为等边三角形．设线段BC与y轴交于点D，则BD＝CD，且∠OCD＝30°，又∵OB＝OC＝OA＝2，∴CD＝OC•cos30°＝，OD＝OC•sin30°＝1．不妨设点C在y轴右侧，则点C的坐标为（，﹣1）．∵点C在抛物线上，且c＝2，b＝0，∴3a+2＝﹣1，∴a＝﹣1，∴抛物线的解析式为y＝﹣x2+2．②证明：由①可知，点M的坐标为（x1，﹣+2），点N的坐标为（x2，﹣+2）．直线OM的解析式为y＝k1x（k1≠0）．∵O、M、N三点共线，∴x1≠0，x2≠0，且＝，∴﹣x1+＝﹣x2+，∴x1﹣x2＝﹣，∴x1x2＝﹣2，即x2＝﹣，∴点N的坐标为（﹣，﹣+2）．设点N关于y轴的对称点为点N′，则点N′的坐标为（，﹣+2）．∵点P是点O关于点A的对称点，∴OP＝2OA＝4，∴点P的坐标为（0，4）．设直线PM的解析式为y＝k2x+4，∵点M的坐标为（x1，﹣+2），∴﹣+2＝k2x1+4，∴k2＝﹣，∴直线PM的解析式为y＝﹣x+4．∵﹣•+4＝＝﹣+2，∴点N′在直线PM上，∴PA平分∠MPN．14．如图，已知二次函数y＝ax2+bx+3（a≠0）的图象经过点A（3，0），B（4，1），且与y 轴交于点C，连接AB、AC、BC．（1）求此二次函数的关系式；（2）判断△ABC的形状；若△ABC的外接圆记为⊙M，请直接写出圆心M的坐标；（3）若将抛物线沿射线BA方向平移，平移后点A、B、C的对应点分别记为点A1、B1、C1，△A1B1C1的外接圆记为⊙M1，是否存在某个位置，使⊙M1经过原点？若存在，求出此时抛物线的关系式；若不存在，请说明理由．解：（1）把点A（3，0），B（4，1）代入y＝ax2+bx+3中，，解得：，所以所求函数关系式为：y＝x2﹣x+3；（2）△ABC是直角三角形，过点B作BD⊥x轴于点D，易知点C坐标为：（0，3），所以OA＝OC，所以∠OAC＝45°，又∵点B坐标为：（4，1），∴AD＝BD，∴∠DAB＝45°，∴∠BAC＝180°﹣45°﹣45°＝90°，∴△ABC是直角三角形，圆心M的坐标为：（2，2）；（3）存在取BC的中点M，过点M作ME⊥y轴于点E，∵M的坐标为：（2，2），∴MC＝＝，OM＝2，∴∠MOA＝45°，又∵∠BAD＝45°，∴OM∥AB，∴要使抛物线沿射线BA方向平移，且使⊙M1经过原点，则平移的长度为：2﹣或2+；∵∠BAD＝45°，∴抛物线的顶点向左、向下均分别平移＝个单位长度或＝个单位长度，∵y＝x2﹣x+3＝（x﹣）2﹣，∴平移后抛物线的关系式为：y＝（x﹣+）2﹣﹣，即y＝（x﹣）2﹣，或y＝（x﹣+）2﹣﹣，即y＝（x﹣）2﹣．综上所述，存在一个位置，使⊙M1经过原点，此时抛物线的关系式为：y＝（x﹣）2﹣或y＝（x﹣）2﹣．15．已知抛物线C1：y＝ax2过点（2，2）（1）直接写出抛物线的解析式y＝x2；（2）如图，△ABC的三个顶点都在抛物线C1上，且边AC所在的直线解析式为y＝x+b，若AC边上的中线BD平行于y轴，求的值；（3）如图，点P的坐标为（0，2），点Q为抛物线上C1上一动点，以PQ为直径作⊙M，直线y＝t与⊙M相交于H、K两点是否存在实数t，使得HK的长度为定值？若存在，求出HK的长度；若不存在，请说明理由．解：（1）把点（2，2）坐标代入y＝ax2，解得：a＝，∴抛物线的解析式为y＝x2；（2）把y＝x+b和y＝x2得：x2﹣2x﹣2b＝0，设A、C两点的坐标为（x1，y1）、（x2，y2），则：x1+x2＝2，x1•x2＝﹣2b，点D坐标为（，），即；D（1，1+b），B坐标为（1，），AC2＝[（x2﹣x1）]2＝16b+8BD＝+b，∴＝16；（3）设点Q坐标为（a，a2），点P的坐标为（0，2），由P、Q坐标得点M的坐标为（，a2+1），设圆的半径为r，由P（0，2）、M两点坐标可以求出r2＝+（a2﹣1）2＝a4﹣a2+1，设点M到直线y＝t的距离为d，则d2＝（a2+1﹣t）2＝a4+a2+1+t2﹣2t﹣a2t，则HK＝2＝2，当t﹣＝0时，HK为常数，t＝，HK＝．16．定义：平面直角坐标系xOy中，过二次函数图象与坐标轴交点的圆，称为该二次函数的坐标圆．（1）已知点P（2，2），以P为圆心，为半径作圆．请判断⊙P是不是二次函数y＝x2﹣4x+3的坐标圆，并说明理由；（2）如图1，已知二次函数y＝x2﹣4x+4图象的顶点为A，坐标圆的圆心为P，求△POA 周长的最小值；（3）如图2，已知二次函数y＝ax2﹣4x+4（0＜a＜1）图象交x轴于点A，B，交y轴于点C，与坐标圆的第四个交点为D，连结PC，PD．若∠CPD＝120°，求a的值．解：（1）对于二次函数y＝x2﹣4x+3，当x＝0时，y＝3；当y＝0时，解得x＝1或x＝3，∴二次函数图象与x轴交点为A（1，0），B（3，0），与y轴交点为C（0，3），∵点P（2，2），∴PA＝PB＝PC＝，∴⊙P是二次函数y＝x2﹣4x+3的坐标圆．（2）如图1，连接PH，∵二次函数y＝x2﹣4x+4图象的顶点为A，坐标圆的圆心为P，∴A（2，0），与y轴的交点H（0，4），∴△POA周长＝PO+PA+OA＝PO+PH+2≥OH+2＝6，∴△POA周长的最小值为6．（3）如图2，连接CD，PA，设二次函数y＝ax2﹣4x+4图象的对称轴l与CD交于点E，与x轴交于点F，由对称性知，对称轴l经过点P，且l⊥CD，∵AB＝，∴AF＝BF＝，∵∠CPD＝120°，PC＝PD，C（0，4），∴∠PCD＝∠PDC＝30°，设PE＝m，则PA＝PC＝2m，CE＝m，PF＝4﹣m，∵二次函数y＝ax2﹣4x+4图象的对称轴l为，∴，即，在Rt△PAF中，PA2＝PF2+AF2，∴，即，化简，得，解得，∴．17．如图，在平面直角坐标系中，抛物线y＝x2﹣bx﹣c交x轴于点A，B，点B的坐标为（4，0），与y轴于交于点C（0，﹣2）．（1）求此抛物线的解析式；（2）在抛物线上取点D，若点D的横坐标为5，求点D的坐标及∠ADB的度数；（3）在（2）的条件下，设抛物线对称轴l交x轴于点H，△ABD的外接圆圆心为M（如图1），过点B作⊙M的切线交于点P（如图2），设Q为⊙M上一动点，则在点运动过程中的值是否变化？若不变，求出其值；若变化，请说明理由．解：（1）将点B、C的坐标代入抛物线表达式得：，解得：，∴抛物线的解析式为y＝x2﹣x﹣2；（2）当x＝5时，y＝x2﹣x﹣2＝3，故D的坐标为（5，3），令y＝0，则x＝4（舍去）或﹣1，故点A（﹣1，0），如图，连接BD，作BN⊥AD于N，∵A（﹣1，0），B（4，0），C（0，﹣2），∴AD＝3，BD＝，AB＝5，＝＝，∵S△ABD∴BN＝，∴sin∠BDN＝＝＝，∴∠BDN＝45°，∴∠ADB＝∠BDN＝45°；（3）不变．如图，连接MQ，MB，∵过点B作⊙M的切线交1于点P，∴∠MBP＝90°，∵∠MBO＝45°，∴∠PBH＝45°，∴PH＝HB＝2.5，∵＝＝，＝＝，∵∠HMQ＝∠QMP，∴△HMQ∽△QMP，∴＝＝，∴在点Q运动过程中的值不变，其值为．18．如图，抛物线y＝ax2+bx+c（a≠0），与x轴交于A（4，0）、O两点，点D（2，﹣2）为抛物线的顶点．（1）求该抛物线的解析式；（2）点E为AO的中点，以点E为圆心、以1为半径作⊙E，交x轴于B、C两点，点M为⊙E上一点．①射线BM交抛物线于点P，设点P的横坐标为m，当tan∠MBC＝2时，求m的值；②如图2，连接OM，取OM的中点N，连接DN，则线段DN的长度是否存在最大值或最小值？若存在，请求出DN的最值；若不存在，请说明理由．解：（1）由抛物线顶点式表达式得：y＝a（x﹣2）2﹣2，将点A的坐标代入上式并解得：a＝，故抛物线的表达式为：y＝（x﹣2）2﹣2＝x2﹣2x①；（2）①点E是OA的中点，则点E（2，0），圆的半径为1，则点B（1，0），当点P在x轴下方时，如图1，∵tan∠MBC＝2，故设直线BP的表达式为：y＝﹣2x+s，将点B（1，0）的坐标代入上式并解得：s＝2，故直线BP的表达式为：y＝﹣2x+2②，联立①②并解得：x＝±2（舍去﹣2），故m＝2；当点P在x轴上方时，同理可得：m＝4±2（舍去4﹣2）；故m＝2或4+2；②存在，理由：连接BN、BD、EM，则BN是△OEM的中位线，故BN＝EM＝，而BD＝＝，在△BND中，BD﹣BN≤ND≤BD+BN，即﹣0.5≤ND≤+0.5，故线段DN的长度最小值和最大值分别为﹣0.5和+0.5．19．如图，在平面直角坐标系上，一条抛物线y＝ax2+bx+c（a≠0）经过A（1，0）、B（3，0）、C（0，3）三点，连接BC并延长．（1）求抛物线的解析式；（2）点M是直线BC在第一象限部分上的一个动点，过M作MN∥y轴交抛物线于点N．1°求线段MN的最大值；2°当MN取最大值时，在线段MN右侧的抛物线上有一个动点P，连接PM、PN，当△PMN的外接圆圆心Q在△PMN的边上时，求点P的坐标．解：（1）把A、B、C三点的坐标代入抛物线y＝ax2+bx+c（a≠0）中，得，解得，，∴抛物线的解析式为：y ＝x 2﹣4x +3；（2）1°设直线BC 的解析式为y ＝mx +n （m ≠0），则，解得，，∴直线BC 的解析式为：y ＝﹣x +3，设M （t ，﹣t +3）（0＜t ＜3），则N （t ，t 2﹣4t +3），∴MN ＝﹣t 2+3t ＝﹣，∴当t ＝时，MN 的值最大，其最大值为；2°∵△PMN 的外接圆圆心Q 在△PMN 的边上，∴△PMN 为直角三角形，由1°知，当MN 取最大值时，M （），N （），①当∠PMN ＝90°时，PM ∥x 轴，则P 点与M 点的纵坐标相等，∴P 点的纵坐标为，当y ＝时，y ＝x 2﹣4x +3＝，解得，x ＝，或x ＝（舍去），∴P （）；②当∠PNM ＝90°时，PN ∥x 轴，则P 点与N 点的纵坐标相等，∴P 点的纵坐标为﹣，当y ＝﹣时，y ＝x 2﹣4x +3＝﹣，解得，x ＝，或x ＝（舍去），∴P （，）；③当∠MPN ＝90°时，则MN 为△PMN 的外接圆的直径，∴△PMN的外接圆的圆心Q为MN的中点，∴Q（），半径为，过Q作QK∥x轴，与在MN右边的抛物线图象交于点K，如图②，令y＝，得y＝x2﹣4x+3＝，解得，x＝＜（舍），或x＝，∴K（，），∴QK＝＞，即K点在以MN为直径的⊙Q外，设抛物线y＝x2﹣4x+3的顶点为点L，则l（2，﹣1），连接LK，如图②，则L到QK的距离为，LK＝，设Q点到LK的距离为h，则，∴＝，∴直线LK下方的抛物线与⊙Q没有公共点，∵抛物线中NL部分（除N点外）在过N点与x轴平行的直线下方，∴抛物线中NL部分（除N点外）与⊙Q没有公共点，∵抛物线K点右边部分，在过K点与y轴平行的直线的右边，∴抛物线K点右边部分与⊙Q没有公共点，综上，⊙Q与MN右边的抛物线没有交点，∴在线段MN右侧的抛物线上不存在点P，使△PMN的外接圆圆心Q在MN边上；综上，点P的坐标为（）或（）．20．如图1，在平面直角坐标系xOy中，抛物线y＝ax2+bx+c与x轴分别相交于A、B两点，与y轴相交于点C，下表给出了这条抛物线上部分点（x，y）的坐标值：x…﹣10123…y…03430…（1）求出这条抛物线的解析式；（2）如图1，直线y＝kx+1（k＜0）与抛物线交于P，Q两点，交抛物线的对称轴于点T，若△QMT的面积是△PMT面积的两倍，求k的值；（3）如图2，点D是第四象限内抛物线上一动点，过点D作DF⊥x轴，垂足为F，△ABD的外接圆与DF相交于点E．试问：线段EF的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由．解：（1）根据表格可得出A（﹣1，0），B（3，0），C（0，3），设抛物线解析式为y＝a（x+1）（x﹣3），将C（0，3）代入，得：3＝a（0+1）（0﹣3），解得：a＝﹣1，∴y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3，∴该抛物线解析式为y＝﹣x2+2x+3；（2）设P（x1，y1），Q（x2，y2），令y＝kx+1＝﹣x2+2x+3，整理得：x2+（k﹣2）x﹣2＝0，∴x1+x2＝2﹣k，x1x2＝﹣2①，∵△QMT的面积是△PMT面积的两倍，∴MT•（x2﹣1）＝2×MT•（1﹣x1），∴2x1+x2＝3，即x2＝3﹣2x1②，将②代入①得：2x12﹣3x1﹣2＝0，解得：x1＝2或，∴或，∴k＝1或，∵k＜0，∴k＝﹣；（3）线段EF的长为定值1，如图，连接BE，设D（t，﹣t2+2t+3），且t＞3，∵EF⊥x轴，∴DF＝﹣（﹣t2+2t+3）＝t2﹣2t﹣3，∵F（t，0），∴BF＝OF﹣OB＝t﹣3，AF＝t﹣（﹣1）＝t+1，∵四边形ABED是圆内接四边形，∴∠DAF+∠BED＝180°，∵∠BEF+∠BED＝180°，∴∠DAF＝∠BEF，∵∠AFD＝∠EFB＝90°，∴△AFD∽△EFB，∴，∴，∴EF＝＝＝1，∴线段EF的长为定值1．21．如图，抛物线y＝﹣x2+2x+3与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．（1）直接写出A、B、C三点的坐标和抛物线的对称轴．（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m．①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？②△BCF的面积为S，求S与m的函数关系式，并求出S的最大值．（3）现有一个以原点O为圆心，长为半径的圆沿y轴正半轴方向向上以每秒1个单位的速度运动，问几秒后⊙O与直线AC相切？解：（1）设0＝﹣x2+2x+3，解得：x＝﹣1或3，∵抛物线y＝﹣x2+2x+3与x相交于AB（点A点B左侧），∴A（﹣1，0），B（3，0），∵抛物线与y轴相交于点C，∴C（0，3），∴抛物线的对称轴是：直线x＝1．（2）①设直线BC的函数关系式为y＝kx+b，把B（3，0），C（0，3）分别代入，得，解得：k＝﹣1，b＝3∴直线BC的函数关系式为y＝﹣x+3．当x＝1时，y＝﹣1+3＝2，∴E（1.2）．当x＝m时，y＝﹣m+3，∴P（m，﹣m+3）在y＝﹣x2+2x+3中，当x＝1时，y＝4，∴D（1，4）．当x＝m时，y＝﹣m2+2m+3，∴F（m，﹣m2+2m+3），∴线段DE＝4﹣2＝2，线段PF＝﹣m2+2m+3﹣（﹣m+3）＝﹣m2+3m，∵PF∥DE∴当PF＝DE时，四边形PEDF为平行四边形．由﹣m2+3m＝2，解得m＝2或m＝1（不合题意，舍去）．因此，当m＝2时，四边形PEDF为平行四边形．②设直线PF与x轴交于点M，由B（3，0），O（0，0），可得OB＝OM+MB＝3．+S△CPF，∵S＝S△EPF即S＝PF•BM+PF•OM＝PF（BM+OM）＝PF•OB，∴S＝×3（﹣m2+3m）＝﹣m2+m（0≤m≤3）∴当m＝﹣＝时S最大值＝；。

二次函数与圆综合提高（压轴题）1、如图，在等边△ABC中，AB=3，D、E分别是AB、AC上的点，且DE∥BC，将△ADE沿DE 翻折，与梯形BCED重叠的部分记作图形L．（1）求△ABC的面积；（2）设AD=x，图形L的面积为y，求y关于x的函数解析式；∴MO=OE，∠MOE=120°，∴∠OME=30°，∴∠DME=90°，∴DE是直径，S⊙O=π×12=π．2、（2013•压轴题）如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，4），点B的坐标为（4，0），点C的坐标为（﹣4，0），点P在射线AB上运动，连结CP与y轴交于点D，连结BD．过P，D，B三点作⊙Q与y轴的另一个交点为E，延长DQ交⊙Q于点F，连结EF，BF．（1）求直线AB的函数解析式；（2）当点P在线段AB（不包括A，B两点）上时．①求证：∠BDE=∠ADP；②设DE=x，DF=y．请求出y关于x的函数解析式；（3）请你探究：点P在运动过程中，是否存在以B，D，F为顶点的直角三角形，满足两条直角边之比为2：1？如果存在，求出此时点P的坐标：如果不存在，请说明理由．解：（1）设直线AB的函数解析式为y=kx+4，代入（4，0）得：4k+4=0，解得：k=﹣1，则直线AB的函数解析式为y=﹣x+4；（2）①由已知得：OB=OC，∠BOD=∠COD=90°，又∵OD=OD，∴△BOD≌△COD，∴∠BOD=∠CDO，∵∠CDO=∠ADP，∴∠BDE=∠ADP，②连结PE，∵∠ADP是△DPE的一个外角，∴∠ADP=∠DEP+∠DPE，∵∠BDE是△ABD的一个外角，∴∠BDE=∠ABD+∠OAB，∵∠ADP=∠BDE，∠DEP=∠ABD，∴∠DPE=∠OAB，∵OA=OB=4，∠AOB=90°，OD=43， ∴点D 的坐标为（0，﹣43）， 直线CD 的解析式为：y=﹣13x ﹣43， 由得：，∴点P 的坐标为（8，﹣4），综上所述，点P 的坐标为（2，2）或（8，﹣4）．3、抛物线y=x ²-bx-3b+3过A 、B 两点（点A 在点B 的左边），交y轴于点C ，且经过点（b －2，2b 2－5b －1）.（1）求这条抛物线的解析式；（2）⊙M 过A 、B 、C 三点，交y 轴于另一点D ，求点M 的坐标；（3）连接AM 、DM ，将∠AMD 绕点M 顺时针旋转，两边MA 、MD 与x轴、y 轴分别交于点E 、F ，若△DMF 为等腰三角形，求点E 的坐标.解析：（1）把点（b －2，2b 2－5b －1）代入解析式，得2b 2－5b －1=（b －2）2+b （b －2）－3b +3， ……………1′解得b =2.∴抛物线的解析式为y =x 2+2x －3. ……………2′（2）由x 2+2x －3=0，得x =－3或x=1.∴A （－3，0）、B （1，0）、C （0，－3）.抛物线的对称轴是直线x =－1，圆心M 在直线x =－1上. ……………3′∴设M （－1，n ），作MG ⊥x 轴于G ，MH ⊥y 轴于H ，连接MC 、MB .∴MH =1，BG =2. ……………4′∵MB =MC ，∴BG 2+MG 2=MH 2+CH 2，即4+n 2=1+（3+n ）2，解得n=－1，∴点M （－1，－1） ……………5′（3）如图，由M （－1，－1），得MG =MH .∵MA =MD ，∴Rt △AMG ≌RtDMH ，∴∠1=∠2.由旋转可知∠3=∠4. ∴△AME ≌△DMF .若△DMF 为等腰三角形，则△AME 为等腰三角形. ……………6′设E （x ，0），△AME 为等腰三角形，分三种情况：①AE =AM =5，则x=5－3，∴E （5－3，0）；②∵M 在AB 的垂直平分线上，∴MA =ME =MB ，∴E （1，0） ……………7′③点E 在AM 的垂直平分线上，则AE =ME .AE =x +3，ME 2=MG 2+EG 2=1+（－1－x ）2，∴（x +3）2=1+（－1－x ）2，解得x =47-，∴E （47-，0）. ∴所求点E 的坐标为（5－3，0），（1，0），（47-，0） ……………8′4、（2013•压轴题）如图，已知抛物线y=ax2+bx﹣2（a≠0）与x轴交于A、B两点，与y轴交于C点，直线BD交抛物线于点D，并且D（2，3），tan∠DBA=．（1）求抛物线的解析式；（2）已知点M为抛物线上一动点，且在第三象限，顺次连接点B、M、C、A，求四边形BMCA 面积的最大值；（3）在（2）中四边形BMCA面积最大的条件下，过点M作直线平行于y轴，在这条直线上是否存在一个以Q点为圆心，OQ为半径且与直线AC相切的圆？若存在，求出圆心Q的坐标；若不存在，请说明理由．：解：（1）如答图1所示，过点D作DE⊥x轴于点E，则DE=3，OE=2．∵tan∠DBA==，∴BE=6，∴OB=BE﹣OE=4，∴B（﹣4，0）．∵点B（﹣4，0）、D（2，3）在抛物线y=ax2+bx﹣2（a≠0）上，∴，解得，∴抛物线的解析式为：y=x2+x﹣2．（2）抛物线的解析式为：y=x2+x﹣2，令x=0，得y=﹣2，∴C（0，﹣2），令y=0，得x=﹣4或1，∴A（1，0）．设点M坐标为（m，n）（m＜0，n＜0），如答图1所示，过点M作MF⊥x轴于点F，则MF=﹣n，OF=﹣m，BF=4+m．S四边形BMCA=S△BMF+S梯形MFOC+S△AOC=BF•MF+（MF+OC）•OF+OA•OC=（4+m）×（﹣n）+（﹣n+2）×（﹣m）+×1×2=﹣2n﹣m+1∵点M（m，n）在抛物线y=x2+x﹣2上，∴n=m2+m﹣2，代入上式得：S四边形BMCA=﹣m2﹣4m+5=﹣（m+2）2+9，∴当m=﹣2时，四边形BMCA面积有最大值，最大值为9．（3）假设存在这样的⊙Q．如答图2所示，设直线x=﹣2与x轴交于点G，与直线AC交于点F．设直线AC的解析式为y=kx+b，将A（1，0）、C（0，﹣2）代入得：，解得：k=2，b=﹣2，∴直线AC解析式为：y=2x﹣2，令x=﹣2，得y=﹣6，∴F（﹣2，﹣6），GF=6．在Rt△AGF中，由勾股定理得：AF===3．设Q（﹣2，n），则在Rt△AGF中，由勾股定理得：OQ==．设⊙Q与直线AC相切于点E，则QE=OQ=．坐标为（﹣1，0），以AB的中点P为圆心，AB为直径作⊙P的正半轴交于点C．（1）求经过A、B、C三点的抛物线所对应的函数解析式；（2）设M为（1）中抛物线的顶点，求直线MC对应的函数解析式；∴MC与⊙P的位置关系是相切．6、（2013•压轴题）如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，二次函数y=ax2+bx+c的图象经过点A，B，与x轴分别交于点E，F，且点E的坐标为（﹣23，0），以0C为直径作半圆，圆心为D．（1）求二次函数的解析式；（2）求证：直线BE是⊙D的切线；（3）若直线BE与抛物线的对称轴交点为P，M是线段CB上的一个动点（点M与点B，C 不重合），过点M作MN∥BE交x轴与点N，连结PM，PN，设CM的长为t，△PMN的面积为S，求S与t的函数关系式，并写出自变量t的取值围．S是否存在着最大值？若存在，求出最大值；若不存在，请说明理由．解答：解：（1）由题意，得A（0，2），B（2，2），E的坐标为（﹣23，0），则，解得，，∴该二次函数的解析式为：y=﹣98x2+94x+2；（2）如图，过点D作DG⊥BE于点G．由题意，得ED=+1=，EC=2+=，BC=2，∴BE==．∵∠BEC=∠DEG，∠EGD=∠ECB=90°，∴△EGD∽△ECB，∴=，∴DG=1．∵⊙D的半径是1，且DG⊥BE，∴BE是⊙D的切线；（3）由题意，得E（﹣23，0），B（2，2）．设直线BE为y=kx+h（k≠0）．则，解得，，∴直线BE为：y=34x+12．∵直线BE与抛物线的对称轴交点为P，对称轴直线为x=1，∴点P的纵坐标y=54，即P（1，54）．∵MN∥BE， ∴∠MNC=∠BEC．∵∠C=∠C=90°，∴△MNC∽△BEC，∴=，∴=2t ，则CN=43t ， ∴DN=t﹣1，∴S △PND =12DN•PD=5568t -． S △MNC =12CN•CM=23t 2． S 梯形PDCM =（12PD+CM ）•CD=5182t +． ∵S=S △PND +S 梯形PDCM ﹣S △MNC =﹣+t （0＜t ＜2）．∵抛物线S=﹣+t （0＜t ＜2）的开口方向向下，∴S 存在最大值．当t=1时，S 最大=23． 7、（2013•）已知：一元二次方程x +kx+k ﹣=0．（1）求证：不论k 为何实数时，此方程总有两个实数根；（2）设k ＜0，当二次函数y=x 2+kx+k ﹣的图象与x 轴的两个交点A 、B 间的距离为4时，求此二次函数的解析式；（3）在（2）的条件下，若抛物线的顶点为C ，过y 轴上一点M （0，m ）作y 轴的垂线l ，当m 为何值时，直线l 与△ABC 的外接圆有公共点？（1）证明：∵△=k 2﹣4××（k ﹣）=k 2﹣2k+1=（k ﹣1）2≥0，∴关于x 的一元二次方程x 2+kx+k ﹣=0，不论k 为何实数时，此方程总有两个实数根；（2）令y=0，则x 2+kx+k ﹣=0．∵x A +x B =﹣2k ，x A •x B =2k ﹣1，∴|x A ﹣x B |===2|k ﹣1|=4，即|k ﹣1|=2，解得k=3（不合题意，舍去），或k=﹣1．∴此二次函数的解析式是y=x 2﹣x ﹣；（3）由（2）知，抛物线的解析式是y=x 2﹣x ﹣．易求A （﹣1，0），B （3，0），C （1，﹣2），∴AB=4，AC=2，BC=2．显然AC 2+BC 2=AB 2，得△ABC 是等腰直角三角形．AB 为斜边，∴外接圆的直径为AB=4，∴﹣2≤m≤2．8、（2013•压轴题）如图，已知抛物线y=ax +bx+c （a≠0）的顶点坐标为（4，﹣），且与y轴交于点C （0，2），与x 轴交于A ，B 两点（点A 在点B 的左边）．（1）求抛物线的解析式及A ，B 两点的坐标；（2）在（1）中抛物线的对称轴l上是否存在一点P，使AP+CP的值最小？若存在，求AP+CP 的最小值，若不存在，请说明理由；（3）在以AB为直径的⊙M相切于点E，CE交x轴于点D，求直线CE的解析式．解：（1）由题意，设抛物线的解析式为y=a（x﹣4）2﹣（a≠0）∵抛物线经过（0，2）∴a（0﹣4）2﹣=2解得：a=∴y=（x﹣4）2﹣即：y=x2﹣x+2当y=0时，x2﹣x+2=0解得：x=2或x=6∴A（2，0），B（6，0）；（2）存在，如图2，由（1）知：抛物线的对称轴l为x=4，因为A、B两点关于l对称，连接CB交l于点P，则AP=BP，所以AP+CP=BC的值最小∵B（6，0），C（0，2）∴OB=6，OC=2∴BC=2，∴AP+CP=BC=2∴AP+CP的最小值为2；（3）如图3，连接ME∵CE是⊙M的切线∴ME⊥CE，∠CEM=90°由题意，得OC=ME=2，∠ODC=∠MDE∵在△COD与△MED中∴△COD≌△MED（AAS），∴OD=DE，DC=DM设OD=x则CD=DM=OM﹣OD=4﹣x则RT△COD中，OD2+OC2=CD2，∴x2+22=（4﹣x）2∴x=∴D（，0）设直线CE的解析式为y=kx+b∵直线CE过C（0，2），D（，0）两点，则解得：∴直线CE的解析式为y=﹣+2；圆的圆心坐标为C （2，0），B 是第一象限圆弧上的一点，且BC ⊥AC ，抛物线c bx x y ++-=221经过C 、B 两点，与x 轴的另一交点为D 。

圆与二次函数综合题1. 抛物线交x轴于A、B两点，交y轴于点C，已知抛物线的对称轴为x=1，B(3，0)，C(0，-3).(1)求二次函数的关系式；(2)在抛物线对称轴上是否存在一点P，使P到B、C两点距离之差最大？若存在，求出P点坐标；若不存在，请说明理由；(3)平行于x轴的一条直线交抛物线于M、N两点，若以MN为直径的圆恰好与x轴相切，求此圆的半径.3. 如图,已知抛物线的顶点坐标为M（1,4）,且经过点N（2,3）,与x轴交于A、B 两点（A点在B点左侧）,与y轴交于点C.（1）求抛物线的解析式及A、B、C三点的坐标（2）若直线y=kx+b经过C、M两点,且与x轴交于点D,证明四边形CDAN是平行四边形.（3）点P在抛物线的对称轴x=1上运动,请探索,在x轴上方是否存在这样的点P,使以P为圆心的圆经过A、B两点,且与直线CD相切,若存在,请求出点P的坐标,若不存在,请说明理由.4.已知:如图,抛物线的图象与x轴分别交于A（-3,0）,B（1,0）两点,与y轴交于点（1）求抛物线的顶点E的坐标;（2）求⊙M的面积;（3）连CD交AO于点F,延长CD至G,使FG=2,试探究,当点D运动到何处时,直线GA与⊙M相切,并请说明理由.5.在平面直角坐标系中，抛物线经过O（0，0）、A（4，0）、E（3，）三点（1）求此抛物线的解析式（2）以OA的中点M为圆心，OM长为半径作⊙M，在（1）中的抛物线上是否存在这样的点P，过点P作⊙M的切线l ，且l与x轴的夹角为30°，若存在，请求出此时点P的坐标；若不存在，请说明理由.（注意：本题中的结果可保留根号）6. 已知二次函数的图象如图．（1）求它的对称轴与x轴交点D的坐标；（2）将该抛物线沿它的对称轴向上平移，设平移后的抛物线与x轴，y轴的交点分别为A、B、C三点，若∠ACB=90°，求此时抛物线的解析式；（3）设（2）中平移后的抛物线的顶点为M，以AB为直径，D为圆心作⊙D，试判断直线CM与⊙D的位置关系，并说明理由．参考答案1、(1)将C(0，-3)代入，得c=-3.将c=-3、B(3，0)代入，得9a+3b-3=0.①因为x=1是抛物线的对称轴，所以.②将②变形后代入①得a=1，b=-2.所以二次函数的关系式是.(2)AC与对称轴的交点P即为到B、C的距离之差最大的点. 因为PA=PB，所以点P到B、C两点距离之差就等于|PA-PC|.由于三角形的两边之差小于第三边，所以只有当点P、C、A在一直线上时，|PA-PC|=AC最大. 因为C点的坐标为(0，-3)，A点的坐标为(-1，0)，所以直线AC的关系式是y=-3x-3.又对称轴为x=1，所以点P的坐标(1，-6).(3)设M(，y)、N(，y)，所求圆的半径为r，则，③因为对称轴为x=1，所以.④由③、④得：.⑤将N(r+1，y)代入关系式，得，整理，得.由于r=±y，当y=r>0时，，解得，(舍去)；当y=r<0时，，解得，(舍去).所以此圆的半径是或.2. 解:(1)作AH⊥OB于H,设AD与OC的交点为G∵BC是⊙A的直径∴点A为BC的中点∴AG、AH分别是△BOC的中位线∴AH=12×OC=3√AG=12×OB=1 (三角形的中位线等于第三边的一半)故A点的坐标为(1,3√)(2)∵抛物线过O、B两点∴根据抛物线的对称性,可知抛物线的顶点横坐标为1∵抛物线的顶点在直线y=−(3√3)×x上∴x=1时y=−3√3∴抛物线的顶点坐标为(1,−3√3)设所求抛物线为y=a×x2+bx+c(a≠0)将三点坐标代入抛物线解析式y=a×x2+bx+c中得a=3√3,b=−2×3√3,c=0故抛物线解析式为y=(3√3)×x2−(2×3√3)×x(3)BC=22+(2×3√)2−−−−−−−−−−−√=4∵DE∥x轴A(1,3√) DE=BC=4∴D(-1,3√) E(3,3√)将x=-1代入抛物线解析式中得y=(3√3)+(2×3√3)=3√,故点D在抛物线y=(3√3)×x2−(2×3√3)×x上将x=3代入抛物线解析式得y=3×3√−2×3√=3√,点E在抛物线y=(3√3)×x2−(2×3√3)×x上(4)当点P在抛物线的OD或BE上时,∠BPC为钝角∴X0的取值范围是−1＜X0＜0或2＜X0＜33.(1) 已知顶点M(1,4),抛物线的开口向下则,y-4=k(x-1)2经过N点,则有,3-4=k(2-1)2=k=-1所以,y=-(x-1)2+4.此即抛物线的解析式令y=0,易得：x1-1=2,即x1=3x2-1=-2,即,x2=-1据题意,A(-1,0),B(3,0)令x=0,则,y=-1+4=3,故,C(0,3)(2) 由(1)的解可知,Yc=Yn,则,CN//AB,|CN|=2将C、M的坐标代入直线方程：y=kx+bb=3,4=k×1+3,k=1y=x+3与x轴的交点D（-3,0）,则,|AD|=2线段CN=线段AD,CN//AD.亦即四边形ADCN是平行四边形(3) 设⊙P与CD的切点为G,有PG=PA=PB设P(1,m).由以上计算知道：BD=6,∠CDB=45°PG所在直线方程的斜率k=-1,P在直线PG上,则有y=-x+m+1与y=x+3的交点即Gx=(m-2)/2,y=(m+4)/2.即G[(m-2)/2,(m+4)/2]据PG=PA,有PG2=m2+4=(4-m)2/4+(m-4)2/42m2+8=m2-8m+16m=2√6-4,m=-4-2√6(1,2√6-4),和（1,-4-2√6）即为所求⊙P的圆心坐标4. 1)抛物线y=−3√3x2−23√3x+3√=−3√3(x2+2x+1)+3√+3√3=−3√3(x+1)2+43√3∴E的坐标为(−1,43√3)；(2)连AC；∵M过A,O,C,∠AOC=90∘，∴AC为O的直径。

一、如图，AB为⊙O的直径，EF切⊙O于点D，过点B作BH⊥EF 于点H，交⊙O于点C，连接BD．（1）求证：BD平分∠ABH；（2）如果AB=12，BC=8，求圆心O到BC的距离．二、如图，AB为⊙O的直径，D是⊙O上的一点，过O点作AB的垂线交AD于点E，交BD的延长线于点C，F为CE上一点，且FD=FE。

（1）请探究FD与⊙O的位置关系，并说明理由；（2）若⊙O的半径为2，，求BC的长。

三、如图，AB为⊙O的直径，弦CD⊥AB，垂足为点E，CF⊥AF，且CF=CE.（1）求证：CF是⊙O的切线；（2）若sin∠BAC=2/5，求的值四、在等腰梯形ABCD中，AD∥BC，且AD=2，以CD为直径作⊙O1，交BC于点E，过点E作EF⊥AB于F，建立如图所示的平面直角坐标系，已知A，B两点的坐标分别为A（0，2），B（﹣2，0）。

（1）求C，D两点的坐标；（2）求证：EF为⊙O1的切线；（3）探究：如图，线段CD上是否存在点P，使得线段PC的长度与P 点到y轴的距离相等？如果存在，请找出P点的坐标；如果不存在，请说明理由。

五、如图，AB是⊙O的直径，AC是弦，OD⊥AC于点D，过点A 作⊙O的切线AP，AP与OD的延长线交于点P，连接PC、BC．（1）猜想：线段OD与BC有何数量和位置关系，并证明你的结论．（2）求证：PC是⊙O的切线．六、已知AB=AC，∠BAC=120°，在BC上取一点O，以O为圆心OB为半径作圆，且⊙O过A点，过A作AD∥BC交⊙O于D，求证：（1）AC是⊙O的切线；（2）四边形BOAD是菱形．七、（2012广安）如图，在△ABC中，∠ABC＝∠ACB，以AC为直径的⊙O分别交AB，BC于点M，N，点P在AB的延长线上，且∠CAB＝2∠BCP．（1）求证：直线CP是⊙O的切线；（2）若，，求点B到AC的距离；（3）在（2）的条件下，求△ACP的周长．八、如图，△ABC 内接与⊙O ，AB 是直径，⊙O 的切线PC 交BA的延长线于点P ，OF ∥BC 交AC 于AC 点E ，交PC 于点F ，连接AF ．（1）判断AF 与⊙O 的位置关系并说明理由；（2）若⊙O 的半径为4，AF=3，求AC 的长．九、如图Rt△ABC 的边BC 位于直线l 上，AC=，∠ACB=90o ，∠A=30o ，若△RtABC 由现在的位置向右无滑动地翻转，当点A第3次落在直线上l 时，点A 所经过的路线的长为________________（结果用含л的式子表示）．十、如图，将边长为1cm的等边三角形ABC沿直线l向右翻动（不滑动），点B从开始到结束，所经过路径的长度为（）A．B．C．D．3cm十一、如图，抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B．如图，抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B．（1）求抛物线的解析式；（2）在抛物线上求点M，使△MOB的面积是△AOB面积的3倍；（3）连结OA，AB，在x轴下方的抛物线上是否存在点N，使△OBN 与△OAB相似？若存在，求出N点的坐标；若不存在，说明理由．十二、如图，在△ABC中，∠B=90°，AB=12mm，BC=24mm，动点P从点A开始沿边AB向B以2mm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以4mm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，那么经过（）秒，四边形APQC的面积最小十三、如图二次函数y=x2+bx+c的图象经过A（-1，0）和B （3，0）两点，且交y轴于点C．（1）试确定b、c的值；（2）过点C作CD∥x轴交抛物线于点D，点M为此抛物线的顶点，试确定△MCD的形状．。

圆与二次函数综合题1、已知：二次函数y=x2-kx+k+4的图象与y轴交于点c，且与x轴的正半轴交于A、B两点（点A 在点B左侧）。

若A、B两点的横坐标为整数。

（1）确定这个二次函数的解析式并求它的顶点坐标；（2）若点D的坐标是(0,6），点P（t,0)是线段AB上的一个动点，它可与点A重合，但不与点B重合。

设四边形PBCD的面积为S，求S与t的函数关系式；（3）若点P与点A重合，得到四边形ABCD，以四边形ABCD的一边为边，画一个三角形，使它的面积等于四边形ABCD的面积，并注明三角形高线的长。

再利用“等底等高的三角形面积相等”的知识，画一个三角形，使它的面积等于四边形ABCD的面积（画示意图，不写计算和证明过程）。

2、（1）已知：关于x、y的方程组有两个实数解，求m的取值范围；(2）在（1）的条件下，若抛物线y=-(m-1)x2+(m-5)x+6与x轴交于A、B两点，与y轴交于点C，且△ABC的面积等于12，确定此抛物线及直线y=(m+1)x-2的解析式；（3）你能将（2）中所得的抛物线平移，使其顶点在（2）中所得的直线上吗？请写出一种平移方法。

3、已知：二次函数y=x2-2(m-1)x+m2-2m-3，其中m为实数。

（1）求证：不论m取何实数，这个二次函数的图像与x轴必有两个交点；（2）设这个二次函数的图像与x轴交于点A(x1,0)、B(x2,0),且x1、x2的倒数和为,求这个二次函数的解析式。

4、已知二次函数y1=x2-2x-3. (1)结合函数y1的图像，确定当x取什么值时，y1>0,y1=0,y1<0;(2)根据（1）的结论，确定函数y2= (|y1|-y1)关于x的解析式；（3）若一次函数y=kx+b(k 0)的图像与函数y2的图像交于三个不同的点，试确定实数k与b应满足的条件。

5、已知：如图，直线y= x+ 与x轴、y轴分别交于A、B两点，⊙M经过原点O及A、B两点。

2014中考数学二次函数综合训练1、如图1，已知二次函数图象的顶点坐标为C(1,0)，直线mxy+=与该二次函数的图象交于A、B两点，其中A点的坐标为(3,4)，B点在轴y上.（1）求m的值及这个二次函数的关系式；（2）P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于点E点，设线段PE的长为h，点P的横坐标为x，求h与x之间的函数关系式，并写出自变量x的取值范围；AB上是否存在一点P，使得四边形DCEP是平行四边P点的坐标；若不存在，请说明理由.2、如图2，已知二次函数24y ax x c=-+的图像经过点A和点B．（1）求该二次函数的表达式；（2）写出该抛物线的对称轴及顶点坐标；m＞0），且这两点关于抛物线的对称轴对称，求m的值及点Q 到x轴的图13、如图3，已知抛物线c x b x a y ++=2经过O(0,0)，A(4,0),B(3,3)三点，连结AB ，过点B 作BC ∥x 轴交该抛物线于点C.（1） 求这条抛物线的函数关系式.（2） 两个动点P 、Q 分别从O 、A 两点同时出发,以每秒1个单位长度的速度运动. 其中，点P 沿着线段0A 向A 点运动，点Q 沿着折线A →B →C 的路线向C 点运动. 设这两个动点运动的时间为t （秒) (0＜t ＜4)，△PQA 的面积记为S.① 求S 与t 的函数关系式； ② 当t 为何值时，S 有最大值，最大值是多少？并指出此时△PQA 的形状；③ 是否存在这样的t 值，使得△PQA 是直角三角形?若存在，请直接写出此时P 、Q 两点的坐标；若不存在，请说明理由.4、某公司推出了一种高效环保型除草剂，年初上市后，公司经历了从亏损到盈利的过程. 图4的二次函数图象（部分）刻车了该公司年初以来累积利润S （万元）与时间t （月）之间的关系（即前t 个月的利润总和S 与t 之间的关系）. 根据图象提供信息，解答下列问题：（1）公司从第几个月末开始扭亏为盈；（2）累积利润S 与时间t 之间的函数关系式；（3）求截止到几月末公司累积利润可达30万元；（4）求第8个月公司所获利是多少元？5、如图5，已知抛物线cxbxay++=2的顶点坐标为E（1,0），与y轴的交点坐标为（0,1）.（1）求该抛物线的函数关系式.（2）A、B是x轴上两个动点，且A、B间的距离为AB=4，A在B的左边，过A作AD⊥x轴交抛物线于D，过B作BC⊥x 轴交抛物线于C. 设A点的坐标为（t,0），四边形ABCD的面积为S.P，使得△PAE的周长最小，若存在，请求出点.图5 备用图6)如图6，抛物线223y x x =--与x 轴交A 、B 两点（A 点在B 点左侧），直线l 与抛物线交于A 、C 两点，其中C 点的横坐标为2。