深圳中考(2005-2012)数学试题和答案(超便宜)
- 格式:pdf
- 大小:2.05 MB
- 文档页数:72

2012年广东深圳中考数学真题试卷一、选择题(共12小题;共60分)1. 的倒数是A. B. C. D.2. 第八届中国(深圳)文博会以总成交额元再创新高,将数用科学记数法表示为A. B. C. D.3. 下列图形中,既是轴对称图形,又是中心对称图形的是A. B.C. D.4. 下列运算正确的是A. B. C. D.5. 体育课上,某班两名同学分别进行了次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较这两名学生成绩的A. 平均数B. 频数分布C. 中位数D. 方差6. 如图所示,一个角的三角形纸片,剪去这个角后,得到一个四边形,则的度数为A. B. C. D.7. 端午节吃粽子是中华民族的传统习俗,妈妈买了只红豆粽、只碱水粽、只干肉粽,粽子除内部馅料不同外其它均相同,小颖随意吃一个,吃到红豆粽的概率是A. B. C. D.8. 下列命题:①方程的解是;②的平方根是;③有两边和一角相等的两个三角形全等;④连接任意四边形各边中点的四边形是平行四边形;其中正确的个数有A. 个B. 个C. 个D. 个9. 如图,过原点,且与两坐标轴分别交于点,点,点的坐标为,是第三象限内上一点,,则的半径长为A. B. C. D.10. 已知点关于轴的对称点在第一象限,则的取值范围是A. B. C. D.11. 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为米,坡面上的影长为米.已知斜坡的坡角为,同一时刻,一根长为米且垂直于地面放置的标杆在地面上的影长为米,则树的高度为A. 米B. 米C. 米D. 米12. 如图,已知:,点,,在射线上,点,,在射线上,,,均为等边三角形,若,则的边长为A. B. C. D.二、填空题(共4小题;共20分)13. 因式分解:.14. 二次函数的最小值是.15. 如图,双曲线与在第一象限内交于,两点,分别过,两点向轴和轴作垂线.已知点坐标为,则图中阴影部分的面积为.16. 如图,中,,以斜边为边向外作正方形,且正方形对角线交于点,连接,已知,,则另一直角边的长为.三、解答题(共7小题;共91分)17. 计算:.18. 已知,,求代数式的值.19. 为了了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:(1)本次调查的样本容量为;(2)在表中:,;(3)补全频数分布直方图;(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在分数段内;(5)如果比赛成绩分以上(含分)为优秀,那么你估计该竞赛项目的优秀率大约是.20. 如图,将矩形沿直线折叠,使点与点重合,折痕交于点、交于点,连接、.(1)求证:四边形为菱形;(2)设,,.请写出一个、、三者之间的数量关系式并说明理由.21. “节能环保,低碳生活”是我们倡导的一种生活方式,某家电商场计划用万元购进节能型电视机、洗衣机和空调共台,三种家电的进价和售价如表所示:(1过电视机的数量的倍,请问商场有哪几种进货方案?(2)在“2012 年消费促进月”促销活动期间,商家针对这三种节能型产品推出“现金每购元送元家电消费券一张、多买多送”的活动.在(1)的条件下,若三种电器在活动期间全部售出,商家预估最多送出多少张?22. 如图,已知的三个顶点坐标分别为,,.(1)求经过,,三点的抛物线解析式;(2)设直线交轴于点,连接,求证:;(3)设抛物线与轴交于点,连接交于点,试问以,,为顶点的三角形与相似吗?(4)若点为直线上一动点,当取最小值时,求点的坐标.23. 如图,在平面直角坐标系中,直线的位置随的不同取值而变化.(1)已知的圆心坐标为,半径为.当时,直线经过圆心;当时,直线与相切;(2)若把换成矩形,其三个顶点坐标分别为:,,.设直线扫过矩形的面积为,当由小到大变化时,请求出与的函数关系式.答案第一部分1. D2. B3. C 【解析】根据轴对称图形和中心对称图形的概念判断.4. B5. D6. C7. B8. D9. C 【解析】四边形是圆内接四边形,,.,是的直径,.点的坐标为,,,的半径长.10. B11. A 12. C第二部分13.14.【解析】,当时,函数有最小值.15.16.第三部分原式17.18.当,时,原式19. (1)【解析】此次调查的样本容量为.(2);【解析】;.(3)如图:(4)【解析】中位数为第个数据和第个数据的平均数,而第个数据和第个数据位于这一组,故中位数位于这一组.(5)【解析】将和这两组的频率相加即可得到优秀率,优秀率为.20. (1)四边形是矩形,,.由折叠的性质,可得:,,,...四边形为菱形.(2)、、三者之间的数量关系式为:.理由如下:由折叠的性质,得:.四边形是矩形,.,,,在中,,、、三者之间的数量关系式可写为:.21. (1)设购进电视机台,则洗衣机是台,空调是台,根据题意得:解得:根据是整数,则从到共有个正整数,分别是,,,因而有种方案:方案一:电视机台、洗衣机台、空调台;方案二:电视机台、洗衣机台、空调台;方案三:电视机台、洗衣机台、空调台.(2)三种电器在活动期间全部售出的金额,即.由一次函数性质可知:当最大时,的值最大值是:(元).由现金每购元送元家电消费券一张,可知元的销售总额最多送出张消费券.22. (1)设函数解析式为:,由函数经过点,,,可得解得:故经过,,三点的抛物线解析式为:;(2)设直线的函数解析式为,由题意得:解得:即直线的解析式为.故可得点的坐标为,从而可得:,,故可得出;(3)相似,理由如下:设直线的解析式为,因为,则解得:即直线的解析式为.联立直线与直线的函数解析式可得:解得:即点的坐标为,则,又,.,,,又,.故以,,为顶点的三角形与相似.(4),且,,即为直角三角形,,过点作直线的对称点,点为的中点.,,,,,,即,,,,与的交点.23. (1);【解析】①直线经过圆心时,则有:,;②若直线与相切,如答图 1 所示,应有两条符合条件的切线.设直线与轴、轴交于,点,则,,.由题意,可知与轴相切,设切点为,连接;设直线与的一个切点为,连接并延长交轴于点;过点作于点,轴于点.易证,,.在中,由勾股定理得:,解得:,,,,,代入直线解析式求得:;同理,当切线位于另外一侧时,可求得:.(2)由题意,可知矩形顶点的坐标为.由一次函数的性质可知,当由小到大变化时,直线向右平移,依次扫过矩形的不同部分.可得当直线经过时,;当直线经过时,;当直线经过时,;当直线经过时,.①当时,;②当时,如答图 2 所示.设直线与轴交于点,与交于点.令,可得,;令,可得,.;③当时,如答图 3 所示.设直线与轴交于点,与交于点.令,可得,;令,可得,.;梯形④当时,如答图 4 所示.设直线与交于点,与交于点.令,可得,,;令,可得,,.;矩形⑤当时,矩形.综上所述,当由小到大变化时,与的函数关系式为:.。

2005年深圳市中考数学试题一、选择题:(本大题共10题,每小题3分,共30分)每小题给出四个答案,其中只有一个符合题目的要求,请把选出的答案编号填在下面的答题表一内,否则不给分. 1、在0,-1,1,2这四个数中,最小的数是( )A 、-1B 、0C 、1D 、22、我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图,从图的左面看这个几何体的左视图是( )A B C D 3、方程x 2 = 2x 的解是( )A 、x=2B 、x 1=2 ,x 2= 0C 、x 1=2,x 2=0D 、x = 0 4、长城总长约为6700010米,用科学记数法表示是(保留两个有效数字)( )A 、6.7×105米B 、6.7×106米C 、6.7×107米D 、6.7×108米5、函数y=xk(k ≠0)的图象过点(2,-2),则此函数的图象在平面直角坐标系中的( ) A 、第一、三象限 B 、第三、四象限 C 、A 、第一、二象限 D 、第二、四象限 6、图所列图形中是中心对称图形的为( )A B C D7、中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标中,有5个商标牌的背面注明了一定的奖金额,其余商标的背面是一张苦脸,若翻到它就不得奖。
参加这个游戏的观众有三次翻牌的机会。
某观众前两次翻牌均得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是( ) A 、41 B 、61 C 、51 D 、203 8、实数a 、b 在数轴上的位置如图所示,那么化简|a -b|-2a 的结果是( )A 、2a -bB 、bC 、-bD 、-2a+b 9、一件衣服标价132元,若以9折降价出售,仍可获利10%,则这件衣服的进价是( ) A 、106元 B 、105元 C 、118元 D 、108元 10、如图,AB 是⊙O 的直径,点D 、E 是半圆的三等分点,AE 、BD 的延长线交于点C ,C EDOBAA 、334-π B 、π32 C 、332-π D 、π31二、填空题:(本大题共5小题,每小题3分,共15分,请将答案填入答题表二内,否则不给分)11、一组数据3、8、8、19、19、19、19的众数是________。

2012年广东省深圳市中考数学试卷第一部分 选择题1.3-的倒数是( )A .3B .3-C .13 D .13- 2.第八届中国(深圳)文博会以总成交额143 300 000 000元再创新高,将数143 300 000 000用科学计数法表示为( )A .101.43310⨯ B .111.43310⨯ C .121.43310⨯ D .120.143310⨯ 3.下列图形中,既是轴对称图形,又是中心对称图形的是( )4.下列计算正确的是( )A .235a b ab +=B .235a a a = C .()3326a a = D .639a a a +=5.在体育课上,某班两名同学分别进行了5次短跑训练,要判断哪一名同学的成绩比较稳定,通常要比较这两名学生成绩的( )A .平均数B .频数分布C .中位数D .方差 6.如图1所示,一个60角的三角形纸片,剪去这个60角后,得到一个四边形,则12∠+∠ 的度数为( )A .120B .180C .240D .3007.端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆棕,3只碱水粽,5只感肉粽,粽子除内部馅料不同外其它均相同,小颖随意吃一个,吃到红豆粽的概率是( B ) A .110 B .15 C .13 D .128.下列命题:D① 方程x x =2的解是x =1② 4的平方根是2③ 有两边和一角相等的两个三角形全等④ 连接任意四边形各边中点的四边形是平行四边形 A .4个 B . 3个 C .2个 D .1个9.如图2,⊙C 过原点,且与两坐标轴分别交于点A ,点B ,点的坐标为(0,3),M 是第三象限内OB 上一点,BMO ∠=120,则⊙C 的半径为( )AB C D2160°图1A .6B .5C .3 D.10.已知点(,)123P a a +-关于x 轴的对称点在第一象限,则a 的取值范围是( ) A .a <-1 B .a -<<312C .a -<<312D .a >3211.小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图3,此时测得地面上的影长为8米,坡面上的影长为4米,已知斜坡的坡角为30,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( ) A.(+6米 B .12米 C.(+4米 D .10米12.如图4,已知:MON ∠=30,点A 1、A 2、A 3……在射线ON 上,点B 1、B 2、B 3……在射线OM 上,A B A ∆112、A B A ∆223、A B A ∆334……均为等边三角形,若OA =11,则A B A ∆667的边长为( )A .6B .12C .32D .64第二部分 非选择题二、填空题(本题共4小题, 每小题3分, 共12分) 13.分解因式:a ab -=32。

2012年深圳市中考数学试题(答案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2012年深圳市中考数学试题(答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2012年深圳市中考数学试题(答案)的全部内容。
深圳市2012年初中毕业生学业考试数学试卷第一部分选择题(本部分共12小题,每小题3分,共36分.每小题给出4个选项,其中只有一个是正确的)1.—3的倒数是A .3B .-3 31.c 31.-D 2.第八届中国(深圳)文博会以总成交额143 300 000 000元再创新高.将数143 300 000 000用科学记数法表示为1010433.1.⨯A 1110433.1.⨯B 1210433.1.⨯C 12101433.0.⨯D 3.下列图形中,既是轴对称图形,又是中心对称图形的是4.下列运算正确的是ab b a A 532.=+ 532.a a a B =⋅ 336)2.(a a c = 326.a a a D =÷5.体育课上,某班两名同学分别进行5次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较这两名学生成绩的A .平均数B 。
频数分布 C.中位数 D.方差6.如图1所示,一个60o 角的三角形纸片,剪去这个600角后,得到一个四边形,则么21∠+∠的度数为A 。
120O B. 180O . C 。
240O D 。
30007.端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆粽、3只碱水粽、5只咸肉粽,粽子除内部馅料不同外其它均相同.小颖任意吃一个,吃到红豆粽的概率是101.A 51.B 31.c 21.D 8.下列命题其中真命题有:①方程x x =2的解是1=x ②4的平方根是2③有两边和一角相等的两个三角形全等④连接任意四边形各边中点的四边形是平行四边形A .4个 B.3个 C.2个 D.1个9.如图2,⊙C 过原点,且与两坐标轴分别交于点A 、点B,点A 的坐标为(0,3),M 是第三象限内上一点,∠BM 0=120o ,则⊙C 的半径长为A .6B .5C .3 23.D 10。

2005年广东省初中毕业生学业考试数 学 试 卷一、选择题(本题共5小题,每小题3分,共15分)1.计算的结果是1-的式子是( ) A.1-- B.0(1)- C.(1)--D.11-2.已知1O 的半径为1,2O 的半径为2,两圆的圆心距12O O 为3,则两圆的位置关系是( )A.相交 B.相离C.外切D.内切3.函数1y x=与函数y x =的图象在同一平面直角坐标系内的交点个数是( ) A.1个 B.2个 C.3个 D.0个 4.如图所示几何体的左视图是( )5.4个红球、3个白球、2个黑球放入一个不透明袋子里,从中摸出8个球,恰好红球、白球、黑球都摸到,这件事情() A.可能发生 B.不可能发生 C.很可能发生D.必然发生 二、填空题(本题共5小题,每小题4分,共20分)6.三峡工程电站的总装机容量是18 200 000千瓦,用科学记数法表示电站的总装机容量,应记为千瓦. 7.方程2x =的解是.8.若数据8,9,7,8,x ,3的平均数是7,则这组数据的众数是.9.如图,已知CD AB ⊥,BEAC ⊥,垂足分别为D 、E ,BE 、CD 交于点O ,且AO 平分BAC ∠,那么图中全等三角形共有 对.10.如图,PA 、PB 是O 的切线,点A 、B 为切点,AC 是O 的直径,20BAC ∠=,则P ∠的大小是 度. 三、解答题(一)(本题共5小题,每小题6分,共30分) 11.分解因式224ax ay -; 12.解方程11121x x x ++=-+ 13.将方格中的图案作下列变换,请画出相应的图案:⑴沿y 轴正向平移4个单位;⑵平移后关于y 轴轴对称图形;A. B . C . D . (第4题图) xy B第9题图第10题图14.如图,某长方形广场的四角都有一块半径相同的四分之一圆形的草地,若圆形的半径为宽为b 米.请用代数式表示空地的面积.若长方形长为300米,宽为200米,圆形的半径为10米,求广场空地的面积。
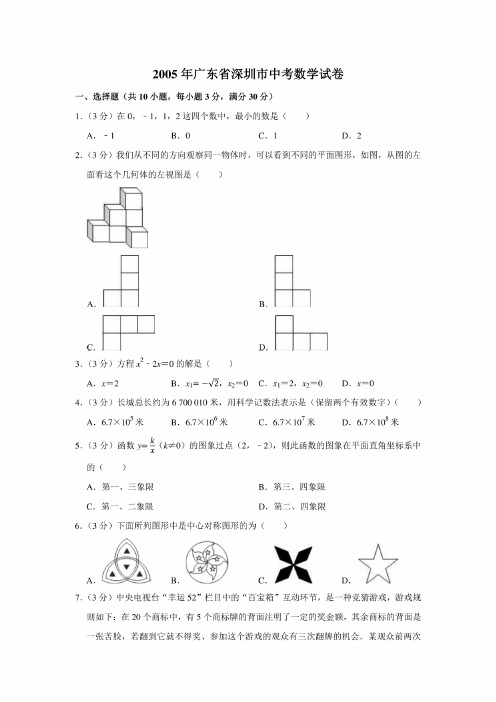
2005年广东省深圳市中考数学试卷一、选择题(共10小题,每小题3分,满分30分)1. (3分)在0, - 1, 1, 2这四个数中,最小的数是( )A. - 1B. 0C. 1D. 22. (3分)我们从不同的方向观察同一物体时, 可以看到不同的平面图形,如图,从图的左面看这个几何体的左视图是( )3. (3分)方程% - 2x=0的解是( )27. (3分)中央电视台''幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标中,有5个商标牌的背面注明了一定的奖金额,其余商标的背面是 一张苦脸,若翻到它就不得奖、参加这个游戏的观众有三次翻牌的机会.某观众前两次A. x=2B . x\— —V2> >2=0 C.工1 = 2,工2=0 D. x=04. (3分)长城总长约为6 700 010米,用科学记数法表示是(保留两个有效数字)(A. 6.7X1()5米B. 6.7X10米6C. 6.7X1()7米D. 6.7X107 8米5. (3分)函数以尹0)的图象过点(2, -2),则此函数的图象在平面直角坐标系中的( )A.第一、三象限B.第三、四象限C.第一、二象限D.第二、四象限翻牌均得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是()1113A.—B.-C.一D.—465208.(3分)实数a、力在数轴上的位置如图所示,那么化简\a-b\-4c?的结果是()------1---------------1-------1-------------->CL0hA.2a- bB.bC.-bD.- 2a+b9.(3分)一件衣服标价132元,若以9折降价出售,仍可获利10%,则这件衣服的进价是()A.106元B.105元C.118元D.108元10.(3分)如图,是OO的直径,点D、E是半圆的三等分点,AE、的延长线交于点C,若CE=2,则图中阴影部分的面积是()422A.V3B.—itC.\/3D.二、填空题(共5小题,每小题3分,满分15分)11.(3分)一组数据3,8,8,19,19,19,19的众数是.12.(3分)下图是根据某地相邻两年6月上旬日平均气温情况绘制的折线统计图,通过观察图形,可以判断这两年6月上旬气温比较稳定的年份是年.III2113111115U6117U8U»U1011(1)2001^6)11JU 1112i]3114115口6117118||9U10IJ(2)2005年6月UiI13.(3分)如图,己知,在△人8。
2005年深圳市中考数学试题考试时间90分钟,满分100分题号 一 二 三 总分 1-10 11-15 16 17 18 19 20 21 22 得分一、选择题:(本大题共10题,每小题3分,共30分)每小题给出四个答案,其中只有一个符合题目的要求,请把选出的答案编号填在下面的答题表一内,否则不给分.答题表一题号 12345678910答案1、在0,-1,1,2这四个数中,最小的数是A 、-1B 、0C 、1D 、22、我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图,从图的左面看这个几何体的左视图是A B C D 3、方程x 2 = 2x 的解是A 、x=2B 、x 1=2 ,x 2= 0C 、x 1=2,x 2=0D 、x = 0 4、长城总长约为6700010米,用科学记数法表示是(保留两个有效数字)A 、6.7×105米B 、6.7×106米C 、6.7×107米D 、6.7×108米5、函数y=xk(k ≠0)的图象过点(2,-2),则此函数的图象在平面直角坐标系中的 A 、第一、三象限 B 、第三、四象限 C 、A 、第一、二象限 D 、第二、四象限 6、图所列图形中是中心对称图形的为A B C D7、中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标中,有5个商标牌的背面注明了一定的奖金额,其余商标的背面是一张苦脸,若翻到它就不得奖。
参加这个游戏的观众有三次翻牌的机会。
某观众前两次翻牌均得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是 A 、41 B 、61 C 、51 D 、203 8、实数a 、b 在数轴上的位置如图所示,那么化简|a -b|-2a 的结果是A 、2a -bB 、bC 、-bD 、-2a+b 9、一件衣服标价132元,若以9折降价出售,仍可获利10%,则这件衣服的进价是 A 、106元 B 、105元 C 、118元 D 、108元10、如图,AB 是⊙O 的直径,点D 、E 是半圆的三等分点,AE 、BD 的延长线交于点C ,若CE=2,则图中阴影部分的面积是 A 、334-π B 、π32 C 、332-π D 、π31二、填空题:(本大题共5小题,每小题3分,共15分,请将答案填入答题表二内,否则不给分)答题表二题号 11 12 13 14 15 答案11、一组数据3、8、8、19、19、19、19的众数是__。
2012年深圳市中考数学试卷一、选择题(本题共12题,每小题3分.共36分,每小题给出4个选项,其中只有一个是正确的)1.(3分)﹣3的倒数是()A.3 B.﹣3 C.D.2.(3分)第八届中国(深圳)文博会以总成交额143 300 000 000元再创新高,将数143 300 000 000用科学记数法表示为()A.1.433×1010B.1.433×1011C.1.433×1012D.0.1433×10123.(3分)下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.4.(3分)下列运算正确的是()A.2a﹣3b=5ab B.a2•a3=a5C.(2a)3=6a3D.a6+a3=a95.(3分)体育课上,某班两名同学分别进行了5次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较这两名学生成绩的()A.平均数B.频数分布 C.中位数D.方差6.(3分)如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为()A.120°B.180°C .240°D.300°7.(3分)端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆粽、3只碱水粽、5只干肉粽,粽子除内部馅料不同外其它均相同,小颖随意吃一个,吃到红豆粽的概率是()A.B.C.D.8.(3分)下列命题①方程x2=x的解是x=1;②4的平方根是2;③有两边和一角相等的两个三角形全等;④连接任意四边形各边中点的四边形是平行四边形;其中正确的个数有()A .4个B.3个C.2个D.1个9.(3分)如图,⊙C 过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内上一点,∠BMO=120°,则⊙C的半径长为()A.6 B.5 C.3 D .310.(3分)已知点P(a+1,2a﹣3)关于x轴的对称点在第一象限,则a的取值范围是()A.a<﹣1 B.﹣1<a<C.﹣<a<1 D.a>11.(3分)小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米且垂直于地面放置的标杆在地面上的影长为2米,则树的高度为()A.(6+)米B.12米C.(4﹣2)米 D.10米12.(3分)如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为()A.6 B.12 C.32 D.64二、填空题(本题共4小题,每小题3分,共12分)13.(3分)因式分解:a3﹣ab2= .14.(3分)二次函数y=x2﹣2x+6的最小值是.15.(3分)如图,双曲线y=(k>0)与⊙O在第一象限内交于P、Q两点,分别过P、Q两点向x轴和y轴作垂线.已知点P坐标为(1,3),则图中阴影部分的面积为.16.(3分)如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6,则另一直角边BC的长为.三、解答题:(本题共7小题,其中第17题5分,第18题6分,第19题7分,第20题8分,第21题8分,第22题9分,第23题9分,)17.(5分)计算:|﹣4|+﹣﹣cos45°.18.(6分)已知a=﹣3,b=2,求代数式的值.19.(7分)为了了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:分数段频数频率60≤x<70 30 0.170≤x<80 90 n80≤x<90 m 0.490≤x≤100 60 0.2请根据以上图表中提供的信息,解答下列问题:(1)本次调查的样本容量为;(2)在表中:m= ,n= ;(3)补全频数分布直方图;(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在分数段内;(5)如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是.20.(8分)如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,(1)求证:四边形AFCE为菱形;(2)设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.21.(8分)“节能环保,低碳生活”是我们倡导的一种生活方式,某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台,三种家电的进价和售价如表所示:价格种类进价(元/台)售价(元/台)电视机5000 5500洗衣机2000 2160空调2400 2700(1)在不超出现有资金的前提下,若购进电视机的数量和洗衣机的数量相同,空调的数量不超过电视机的数量的3倍.请问商场有哪几种进货方案?(2)在“2012年消费促进月”促销活动期间,商家针对这三种节能型产品推出“现金每购1000元送50元家电消费券一张、多买多送”的活动.在(1)的条件下,若三种电器在活动期间全部售出,商家预估最多送出多少张?22.(9分)如图,已知△ABC的三个顶点坐标分别为A(﹣4,0)、B(1,0)、C(﹣2,6).(1)求经过A、B、C三点的抛物线解析式;(2)设直线BC交y轴于点E,连接AE,求证:AE=CE;(3)设抛物线与y轴交于点D,连接AD交BC于点F,试问以A、B、F为顶点的三角形与△ABC相似吗?(4)若点P为直线AE上一动点,当CP+DP取最小值时,求P点的坐标.23.(9分)如图,在平面直角坐标系中,直线l:y=﹣2x+b(b≥0)的位置随b的不同取值而变化.(1)已知⊙M的圆心坐标为(4,2),半径为2.当b= 时,直线l:y=﹣2x+b(b≥0)经过圆心M;当b= 时,直线l:y=﹣2x+b(b≥0)与⊙M相切;(2)若把⊙M换成矩形ABCD,其三个顶点坐标分别为:A(2,0)、B(6,0)、C(6,2).设直线l扫过矩形ABCD 的面积为S,当b由小到大变化时,请求出S与b的函数关系式.2012年广东省深圳市中考数学试卷--答案一、选择题(本题共12分,每小题3分.共36分,每小题给出4个选项,其中只有一个是正确的)1.(3分)﹣3的倒数是()A.3 B.﹣3 C.D.【解答】解:∵(﹣3)×(﹣)=1,∴﹣3的倒数是﹣.故选:D.2.(3分)第八届中国(深圳)文博会以总成交额143 300 000 000元再创新高,将数143 300 000 000用科学记数法表示为()A.1.433×1010B.1.433×1011C .1.433×1012D .0.1433×1012【解答】解:143 300 000 000=1.433×1011.故选B.3.(3分)下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.【解答】解:A、是轴对称图形,但不是中心对称图形,故A错误;B、是中心对称图形,不是轴对称图形,故B错误;C、是轴对称图形,不是中心对称图形,故C错误;D、既是轴对称图形,也是中心对称图形,故D正确.故选:D.4.(3分)下列运算正确的是()A.2a﹣3b=5ab B.a2•a3=a5C.(2a)3=6a3D.a6+a3=a9【解答】解:A、2a与3b不是同类项,不能合并,故A选项错误;B、a2•a3=a5,故B选项正确;C、(2a)3=8a3,故C选项错误;D、a6与a3不是同类项,不能合并,故D选项错误.故选B.5.(3分)体育课上,某班两名同学分别进行了5次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较这两名学生成绩的()A.平均数B.频数分布 C.中位数D.方差【解答】解:由于方差能反映数据的稳定性,需要比较这两名学生了5次短跑训练成绩的方差.故选D.6.(3分)如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为()A.120°B.180°C.240°D.300°【解答】解:根据三角形的内角和定理得:四边形除去∠1,∠2后的两角的度数为180°﹣60°=120°,则根据四边形的内角和定理得:∠1+∠2=360°﹣120°=240°.故选C.7.(3分)端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆粽、3只碱水粽、5只干肉粽,粽子除内部馅料不同外其它均相同,小颖随意吃一个,吃到红豆粽的概率是()A.B.C.D.【解答】解:P(红豆粽)==.故选:B.8.(3分)下列命题①方程x2=x的解是x=1;②4的平方根是2;③有两边和一角相等的两个三角形全等;④连接任意四边形各边中点的四边形是平行四边形;其中正确的个数有()A.4个B.3个C.2个D.1个【解答】解:①方程x2=x的解是x1=0,x2=1,故错误;②4的平方根是±2,故错误;③有两边和夹角相等的两个三角形全等,故错误;④连接任意四边形各边中点的四边形是平行四边形,正确.故正确的个数有1个.故选:D.9.(3分)如图,⊙C过原点,且与两坐标轴分别交于点A、点B ,点A的坐标为(0,3),M是第三象限内上一点,∠BMO=120°,则⊙C的半径长为()A.6 B.5 C.3 D.3【解答】解:∵四边形ABMO是圆内接四边形,∠BMO=120°,∴∠BAO=60°,∵AB是⊙C的直径,∴∠AOB=90°,∴∠ABO=90°﹣∠BAO=90°﹣60°=30°,∵点A的坐标为(0,3),∴OA=3,∴AB=2OA=6,∴⊙C的半径长==3.故选:C .10.(3分)已知点P(a+1,2a﹣3)关于x轴的对称点在第一象限,则a的取值范围是()A.a <﹣1 B.﹣1<a <C.﹣<a<1 D.a >【解答】解:∵点P(a+1,2a﹣3)关于x轴的对称点在第一象限,∴点P在第四象限,∴,解不等式①得,a>﹣1,解不等式②得,a<,所以,不等式组的解集是﹣1<a<.故选:B.11.(3分)小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米且垂直于地面放置的标杆在地面上的影长为2米,则树的高度为()A.(6+)米B.12米C .(4﹣2)米 D.10米【解答】解:延长AC交BF延长线于D点,则∠CFE=30°,作CE⊥BD于E,在Rt△CFE中,∠CFE=30°,CF=4m,∴CE=2(米),EF=4cos30°=2(米),在Rt△CED中,∵同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,CE=2(米),CE:DE=1:2,∴DE=4(米),∴BD=BF+EF+ED=12+2(米)在Rt△ABD中,AB=BD=(12+2)=(+6)(米).故选:A.12.(3分)如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为()A.6 B.12 C.32 D.64【解答】解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∠3=∠4=∠12=60°,∴∠2=120°,∵∠MON=30°,∴∠1=180°﹣120°﹣30°=30°,又∵∠3=60°,∴∠5=180°﹣60°﹣30°=90°,∵∠MON=∠1=30°,∴OA1=A1B1=1,∴A2B1=1,∵△A2B2A3、△A3B3A4是等边三角形,∴∠11=∠10=60°,∠13=60°,∵∠4=∠12=60°,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴∠1=∠6=∠7=30°,∠5=∠8=90°,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2=16,以此类推:A6B6=32B1A2=32.故选:C.二、填空题(本题共4小题,每小题3分,共12分)13.(3分)因式分解:a3﹣ab2= a(a+b)(a﹣b).【解答】解:a3﹣ab2=a(a2﹣b2)=a(a+b)(a﹣b).14.(3分)二次函数y=x2﹣2x+6的最小值是 5 .【解答】解:y=x2﹣2x+6=x2﹣2x+1+5=(x﹣1)2+5,可见,二次函数的最小值为5.故答案为:5.15.(3分)如图,双曲线y=(k>0)与⊙O在第一象限内交于P、Q两点,分别过P、Q两点向x轴和y轴作垂线.已知点P坐标为(1,3),则图中阴影部分的面积为 4 .【解答】解:∵⊙O在第一象限关于y=x对称,y=(k>0)也关于y=x对称,P点坐标是(1,3),∴Q点的坐标是(3,1),∴S阴影=1×3+1×3﹣2×1×1=4.故答案是4.16.(3分)如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6,则另一直角边BC的长为7 .【解答】解法一:如图1所示,过O作OF⊥BC,过A作AM⊥OF,∵四边形ABDE为正方形,∴∠AOB=90°,OA=OB,∴∠AOM+∠BOF=90°,又∠AMO=90°,∴∠AOM+∠OAM=90°,∴∠BOF=∠OAM,在△AOM和△BOF中,,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6,∴根据勾股定理得:CF2+OF2=OC2,解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA ≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.三、解答题:(本题共7小题,其中第17题5分,第18题6分,第19题7分,第20题8分,第21题8分,第22题9分,第23题9分,)17.(5分)计算:|﹣4|+﹣﹣cos45°.【解答】解:原式=4+2﹣1﹣2×=5﹣2=3.18.(6分)已知a=﹣3,b=2,求代数式的值.【解答】解:=÷=÷(a+b)=,当a=﹣3,b=2时,原式==﹣.19.(7分)为了了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:分数段频数频率60≤x<70 30 0.170≤x<80 90 n80≤x<90 m 0.490≤x≤100 60 0.2请根据以上图表中提供的信息,解答下列问题:(1)本次调查的样本容量为300 ;(2)在表中:m= 120 ,n= 0.3 ;(3)补全频数分布直方图;(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在80~90 分数段内;(5)如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是60% .【解答】解:(1)此次调查的样本容量为30÷0.1=300;(2)n==0.3;m=0.4×300=120;(3)如图:(4)中位数为第150个数据和第151个数据的平均数,而第150个数据和第151个数据位于80≤x<90这一组,故中位数位于80≤x<90这一组;(5)将80≤x<90和90≤x≤100这两组的频率相加即可得到优秀率,优秀率为60%.20.(8分)如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,(1)求证:四边形AFCE为菱形;(2)设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.【解答】(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠AEF=∠EFC,由折叠的性质,可得:∠AEF=∠CEF,AE=CE,AF=CF,∴∠EFC=∠CEF,∴CF=CE,∴AF=CF=CE=AE,∴四边形AFCE为菱形;(2)a、b、c三者之间的数量关系式为:a2=b2+c2.理由:由折叠的性质,得:CE=AE,∵四边形ABCD是矩形,∴∠D=90°,∵AE=a,ED=b,DC=c,∴CE=AE=a,在Rt△DCE中,CE2=CD2+DE2,∴a、b、c三者之间的数量关系式为:a2=b2+c2.21.(8分)“节能环保,低碳生活”是我们倡导的一种生活方式,某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台,三种家电的进价和售价如表所示:价格种类进价(元/台)售价(元/台)电视机5000 5500洗衣机2000 2160空调2400 2700(1)在不超出现有资金的前提下,若购进电视机的数量和洗衣机的数量相同,空调的数量不超过电视机的数量的3倍.请问商场有哪几种进货方案?(2)在“2012年消费促进月”促销活动期间,商家针对这三种节能型产品推出“现金每购1000元送50元家电消费券一张、多买多送”的活动.在(1)的条件下,若三种电器在活动期间全部售出,商家预估最多送出多少张?【解答】解:(1)设购进电视机x台,则洗衣机是x台,空调是(40﹣2x)台,根据题意得:,解得:8≤x≤10,根据x是整数,则从8到10共有3个正整数,分别是8、9、10,因而有3种方案:方案一:电视机8台、洗衣机8台、空调24台;方案二:电视机9台、洗衣机9台、空调22台;方案三:电视机10台、洗衣机10台、空调20台.(2)三种电器在活动期间全部售出的金额y=5500x+2160x+2700(40﹣2x),即y=2260x+108000.由一次函数性质可知:当x=10最大时,y的值最大值是:2260×10+108000=130600(元).由现金每购1000元送50元家电消费券一张,可知130600元的销售总额最多送出130张消费券.22.(9分)如图,已知△ABC的三个顶点坐标分别为A(﹣4,0)、B(1,0)、C(﹣2,6).(1)求经过A、B、C三点的抛物线解析式;(2)设直线BC交y轴于点E,连接AE,求证:AE=CE;(3)设抛物线与y轴交于点D,连接AD交BC于点F,试问以A、B、F为顶点的三角形与△ABC相似吗?(4)若点P为直线AE上一动点,当CP+DP取最小值时,求P点的坐标.【解答】方法一:解:(1)设函数解析式为:y=ax2+bx+c,由函数经过点A(﹣4,0)、B(1,0)、C(﹣2,6),可得,解得:,故经过A、B、C三点的抛物线解析式为:y=﹣x2﹣3x+4;(2)设直线BC的函数解析式为y=kx+b,由题意得:,解得:,即直线BC的解析式为y=﹣2x+2.故可得点E的坐标为(0,2),从而可得:AE==2,CE==2,故可得出AE=CE;(3)相似.理由如下:设直线AD 的解析式为y=kx+b,则,解得:,即直线AD的解析式为y=x+4.联立直线AD与直线BC的函数解析式可得:,解得:,即点F 的坐标为(﹣,),则BF==,又∵AB=5,BC==3,∴=,=,∴=,又∵∠ABF=∠CBA,∴△ABF∽△CBA.故以A、B、F为顶点的三角形与△ABC相似.方法二:(1)略.(2)略.(3)若△ABF∽△ABC,则,即AB2=BF×BC,∵A(﹣4,0),D(0,4),∴l AD:y=x+4,l BC:y=﹣2x+2,∴l AD 与l BC的交点F(﹣,),∴AB=5,BF=,BC=3,∴AB 2=25,BF×BC=×3=25,∴AB2=BF×BC,又∵∠ABC=∠ABC,∴△ABF∽△ABC.(4)由(3)知:K AE=,K CE=﹣2,∴K AE×K CE=﹣1,∴AE⊥CE,过C点作直线AE 的对称点C,点E为CC′的中点,∴,,∵C(﹣2,6),E(0,2),∴C′X=2,C′Y=﹣2,∵D(0,4),∴l C′D:y=﹣3x+4,∵l AE:y=x+2,∴l C ′D与l AE的交点P(,).23.(9分)如图,在平面直角坐标系中,直线l:y=﹣2x+b(b≥0)的位置随b的不同取值而变化.(1)已知⊙M的圆心坐标为(4,2),半径为2.当b= 10 时,直线l:y=﹣2x+b(b≥0)经过圆心M;当b= 10±2时,直线l:y=﹣2x+b(b≥0)与⊙M相切;(2)若把⊙M换成矩形ABCD,其三个顶点坐标分别为:A(2,0)、B(6,0)、C(6,2).设直线l扫过矩形ABCD 的面积为S,当b由小到大变化时,请求出S与b的函数关系式.【解答】解:(1)①直线l:y=﹣2x+b(b ≥0)经过圆心M (4,2)时,则有:2=﹣2×4+b,∴b=10;②若直线l :y=﹣2x+b(b≥0)与⊙M相切,如答图1所示,应有两条符合条件的切线.设直线与x轴、y轴交于A、B点,则A(,0)、B(0,b),∴OB=2OA.由题意,可知⊙M与x轴相切,设切点为D,连接MD;设直线与⊙M的一个切点为P,连接MP并延长交x轴于点G;过P点作PN⊥MD于点N,PH⊥x轴于点H.易证△PMN∽△BAO,∴PN:MN=OB:OA=2:1,∴PN=2MN.在Rt△PMN中,由勾股定理得:PM2=PN2+MN2,解得:MN=,PN=,∴PH=ND=MD﹣MN=2﹣,OH=OD﹣HD=OD﹣PN=4﹣,∴P(4﹣,2﹣),代入直线解析式求得:b=10﹣2;同理,当切线位于另外一侧时,可求得:b=10+2.(2)由题意,可知矩形ABCD 顶点D的坐标为(2,2).由一次函数的性质可知,当b由小到大变化时,直线l:y=﹣2x+b(b≥0)向右平移,依次扫过矩形ABCD的不同部分.可得当直线经过A(2,0)时,b=4;当直线经过D(2,2)时,b=6;当直线经过B(6,0)时,b=12;当直线经过C(6,2)时,b=14.①当0≤b ≤4时,S=0;②当4<b ≤6时,如答图2所示.设直线l:y=﹣2x+b与x轴交于点P,与AD交于点Q.令y=0,可得x=,∴AP=﹣2;令x=2,可得y=b﹣4,∴AQ=b﹣4.∴S=S△APQ=AP•AQ=(﹣2)(b﹣4)=b2﹣2b+4;③当6<b≤12时,如答图3所示.设直线l:y=﹣2x+b与x轴交于点P,与CD交于点Q.令y=0,可得x=,∴AP=﹣2;令y=2,可得x=﹣1,∴DQ=﹣3.S=S梯形APQD=(DQ+AP)•AD=b﹣5;④当12<b≤14时,如答图4所示.设直线l:y=﹣2x+b与BC交于点P ,与CD交于点Q.令x=6,可得y=b﹣12,∴BP=b﹣12,CP=14﹣b;令y=2,可得x=﹣1,∴DQ=﹣3,CQ=7﹣.S=S矩形ABCD﹣S△PQC=8﹣CP•CQ=b2+7b﹣41;⑤当b>14时,S=S矩形ABCD=8.综上所述,当b由小到大变化时,S与b的函数关系式为:.。
2005年深圳市中考数学试题考试时间90分钟,满分100分题号 一 二 三 总分 1-10 11-15 16 17 18 19 20 21 22 得分一、选择题:(本大题共10题,每小题3分,共30分)每小题给出四个答案,其中只有一个符合题目的要求,请把选出的答案编号填在下面的答题表一内,否则不给分.答题表一题号 12345678910答案1、在0,-1,1,2这四个数中,最小的数是A 、-1B 、0C 、1D 、22、我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图,从图的左面看这个几何体的左视图是A B C D 3、方程x 2 = 2x 的解是A 、x=2B 、x 1=2 ,x 2= 0C 、x 1=2,x 2=0D 、x = 0 4、长城总长约为6700010米,用科学记数法表示是(保留两个有效数字)A 、6.7×105米B 、6.7×106米C 、6.7×107米D 、6.7×108米5、函数y=xk(k ≠0)的图象过点(2,-2),则此函数的图象在平面直角坐标系中的 A 、第一、三象限 B 、第三、四象限 C 、A 、第一、二象限 D 、第二、四象限 6、图所列图形中是中心对称图形的为A B C D7、中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标中,有5个商标牌的背面注明了一定的奖金额,其余商标的背面是一张苦脸,若翻到它就不得奖。
参加这个游戏的观众有三次翻牌的机会。
某观众前两次翻牌均得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是 A 、41 B 、61 C 、51 D 、203 8、实数a 、b 在数轴上的位置如图所示,那么化简|a -b|-2a 的结果是A 、2a -bB 、bC 、-bD 、-2a+b 9、一件衣服标价132元,若以9折降价出售,仍可获利10%,则这件衣服的进价是 A 、106元 B 、105元 C 、118元 D 、108元10、如图,AB 是⊙O 的直径,点D 、E 是半圆的三等分点,AE 、BD 的延长线交于点C ,若CE=2,则图中阴影部分的面积是 A 、334-π B 、π32 C 、332-π D 、π31二、填空题:(本大题共5小题,每小题3分,共15分,请将答案填入答题表二内,否则不给分)答题表二题号 11 12 13 14 15 答案11、一组数据3、8、8、19、19、19、19的众数是__。