下载文档原格式
线性电阻和非线性电阻的伏安特性曲线一、实验原理当一个元件两端加上电压，元件内有电流通过时，电压与电流之比称为该元件的电阻。
若一个元件两端的电压与通过它的电流成比例，则伏安特性曲线为一条直线，该类元件称为线性元件。
若元件两端的电压与通过它的电流不成比例，则伏安特性曲线不再是直线，而是一条曲线，这类元件称为非线性元件。
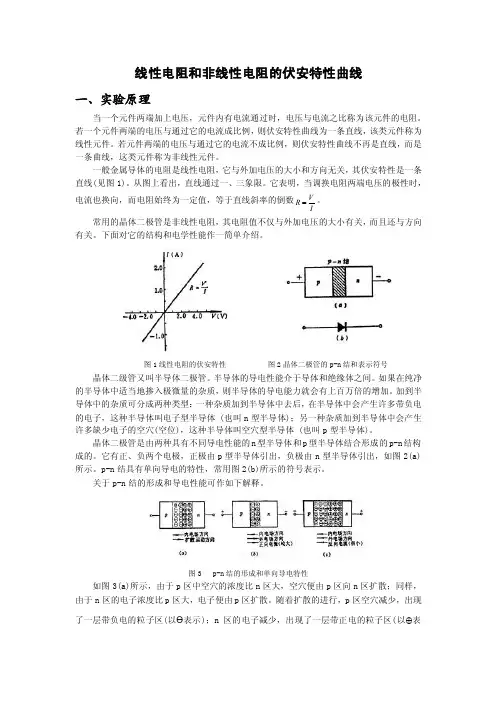
一般金属导体的电阻是线性电阻，它与外加电压的大小和方向无关，其伏安特性是一条直线(见图1)。
从图上看出，直线通过一、三象限。
它表明，当调换电阻两端电压的极性时，电流也换向，而电阻始终为一定值，等于直线斜率的倒数VR。
I常用的晶体二极管是非线性电阻，其电阻值不仅与外加电压的大小有关，而且还与方向有关。
下面对它的结构和电学性能作一简单介绍。
图1线性电阻的伏安特性图2晶体二极管的p-n结和表示符号晶体二级管又叫半导体二极管。
半导体的导电性能介于导体和绝缘体之间。
如果在纯净的半导体中适当地掺入极微量的杂质，则半导体的导电能力就会有上百万倍的增加。
加到半导体中的杂质可分成两种类型：一种杂质加到半导体中去后，在半导体中会产生许多带负电的电子，这种半导体叫电子型半导体 (也叫n型半导体)；另一种杂质加到半导体中会产生许多缺少电子的空穴(空位)，这种半导体叫空穴型半导体 (也叫p型半导体)。
晶体二极管是由两种具有不同导电性能的n型半导体和p型半导体结合形成的p-n结构成的。
它有正、负两个电极，正极由p型半导体引出，负极由n型半导体引出，如图2(a)所示。
p-n结具有单向导电的特性，常用图2(b)所示的符号表示。
关于p-n结的形成和导电性能可作如下解释。
图3 p-n结的形成和单向导电特性如图3(a)所示，由于p区中空穴的浓度比n区大，空穴便由p区向n区扩散；同样，由于n区的电子浓度比p区大，电子便由p区扩散。
随着扩散的进行，p区空穴减少，出现了一层带负电的粒子区(以Ө表示)；n区的电子减少，出现了一层带正电的粒子区(以⊕表示)。
实验四 电路元件伏安特性的测绘一、实验目的1. 学会识别常用电路元件的方法2. 掌握线性电阻、非线性电阻元件伏安特性的逐点测试法3. 掌握实验台上直流电工仪表和设备的使用方法。
二、原理说明任何一个电器二端元件的特性可用该元件上的端电压U 与通过该元件的电流I 之间的函数关系I ＝f(U)来表示，即用I-U 平面上的一条曲线来表征，这条曲线称为该元件的伏安特性曲线。
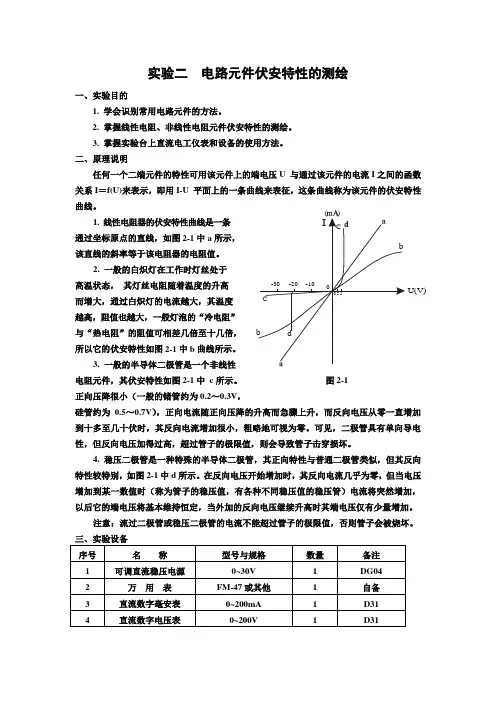
1. 线性电阻器的伏安特性曲线是一条 通过坐标原点的直线，如图4-1中a 所示， 该直线的斜率等于该电阻器的电阻值。
2. 一般的白炽灯在工作时灯丝处于 高温状态， 其灯丝电阻随着温度的升高 而增大，通过白炽灯的电流越大，其温度 越高，阻值也越大，一般灯泡的“冷电阻” 与“热电阻”的阻值可相差几倍至十几倍， 所以它的伏安特性如图4-1中b 曲线所示。
3. 一般的半导体二极管是一个非线性电阻元件，其伏安特性如图4-1中 c 所示。
图4-1 正向压降很小（一般的锗管约为0.2～0.3V ，硅管约为0.5～0.7V ），正向电流随正向压降的升高而急骤上升，而反向电压从零一直增加到十多至几十伏时，其反向电流增加很小，粗略地可视为零。
可见，二极管具有单向导电性，但反向电压加得过高，超过管子的极限值，则会导致管子击穿损坏。
4. 稳压二极管是一种特殊的半导体二极管，其正向特性与普通二极管类似，但其反向特性较特别，如图4-1中d 所示。
在反向电压开始增加时，其反向电流几乎为零，但当电压增加到某一数值时（称为管子的稳压值，有各种不同稳压值的稳压管）电流将突然增加，以后它的端电压将基本维持恒定，当外加的反向电压继续升高时其端电压仅有少量增加。
注意：流过二极管或稳压二极管的电流不能超过管子的极限值，否则管子就会烧坏。
U(V)( )四、实验内容1. 测定线性电阻器的伏安特性按图4-2接线，调节稳压电源的输出电压U ，从0 伏开始缓慢地增加，一直到10V ，记下相应的电压表和电流表的读数U R 、I 。
测绘线性电阻和非线性电阻的伏安特性曲线【实验简介】电阻是电学中常用的物理量。
利用欧姆定律测导体电阻的方法称为“伏安法”。
为了研究材料的导电性，通常作出其伏安特性曲线，了解它的电压和电阻的关系。
伏安特性曲线是直线的元件称为“线性元件”，伏安特性曲线不是直线的元件称为“非线性元件”。
这两种元件的电阻都可以用伏安法测量。
但是，由于测量时电表被引入测量电路，电表内阻必然会影响测量结果，因而应考虑对测量结果进行必要的修正，以减小系统误差。
【实验目的】1、了解电学实验常用仪器的规格、性能，学习它们的使用方法。
2、学习电学实验的基本操作规程和连接电路的一般方法。
3、掌握电阻元件伏安特性的测量方法，用伏安法测电阻。
4、了解系统误差的修正方法，学会作图法处理实验数据。
【实验仪器和用具】名称数量型号1、直流恒压源恒流源1台自备2、数字万用表2台自备3、电阻2只510Ω×1 2200Ω×14、白炽灯泡1只12V/3W5、稳压二极管1只2CW566、短接桥和连接导线若干SJ-009和SJ-3019、九孔插件方板1块SJ-010【实验原理】1、伏安特性曲线实验中常用的线绕电阻、碳膜电阻和金属膜电阻等，它们都具有以下共同特性，即加在该电阻上的电压与通过其上的电流总是成正比例的变化(忽略电流热效应对阻值的影响)。
若以纵坐标表示电流，横坐标表示电压，电流与电压的关系就表示为一条直线如图（a）所示。
具有这种特性的电阻元件成为“线性电阻元件”。
2、非线性电阻如果电阻电阻元件两端的电流、电压关系为曲线，则这类电阻元件称为“非线性电阻元件”（如热敏电阻、二极管等）。
这种元件的特点是电阻随加在它两端的电压改变而改变如图（b）所示。
一般均用伏安特性曲线来反映非线性电阻元件的特性。
欧姆定律告诉我们，通过一段电路的电流，与这段电路两端的电压成正比，与这段电路的电阻成反比，即UI R =。
由此可求得电阻 UR I=（1-1） 这是伏安法测电阻所根据的基本原理。
实验二 电路元件伏安特性的测绘一、实验目的1. 学会识别常用电路元件的方法。
2. 掌握线性电阻、非线性电阻元件伏安特性的测绘。
3. 掌握实验台上直流电工仪表和设备的使用方法。
二、原理说明任何一个二端元件的特性可用该元件上的端电压U 与通过该元件的电流I 之间的函数关系I ＝f(U)来表示，即用I-U 平面上的一条曲线来表征，这条曲线称为该元件的伏安特性曲线。
1. 线性电阻器的伏安特性曲线是一条 通过坐标原点的直线，如图2-1中a 所示， 该直线的斜率等于该电阻器的电阻值。
2. 一般的白炽灯在工作时灯丝处于 高温状态， 其灯丝电阻随着温度的升高 而增大，通过白炽灯的电流越大，其温度 越高，阻值也越大，一般灯泡的“冷电阻” 与“热电阻”的阻值可相差几倍至十几倍， 所以它的伏安特性如图2-1中b 曲线所示。
3. 一般的半导体二极管是一个非线性电阻元件，其伏安特性如图2-1中 c 所示。
图2-1 正向压降很小（一般的锗管约为0.2～0.3V ，硅管约为0.5～0.7V ），正向电流随正向压降的升高而急骤上升，而反向电压从零一直增加到十多至几十伏时，其反向电流增加很小，粗略地可视为零。
可见，二极管具有单向导电性，但反向电压加得过高，超过管子的极限值，则会导致管子击穿损坏。
4. 稳压二极管是一种特殊的半导体二极管，其正向特性与普通二极管类似，但其反向特性较特别，如图2-1中d 所示。
在反向电压开始增加时，其反向电流几乎为零，但当电压增加到某一数值时（称为管子的稳压值，有各种不同稳压值的稳压管）电流将突然增加，以后它的端电压将基本维持恒定，当外加的反向电压继续升高时其端电压仅有少量增加。
注意：流过二极管或稳压二极管的电流不能超过管子的极限值，否则管子会被烧坏。
三、实验设备U(V)( )四、实验内容1. 测定线性电阻器的伏安特性按图4-2接线，调节稳压电源的输出电压U ，从0 伏开始缓慢地增加，一直到10V ，记下相应的电压表和电流表的读数U R 、I 。
线性电阻和非线性电阻的伏安特性曲线【教学目的】1、测绘电阻的伏安特性曲线，学会用图线表示实验结果。
2、了解晶体二极管的单向导电特性。
【教学重点】1、测绘电阻的伏安特性曲线；2、了解二极管的单向导电特性。
【教学难点】非线性电阻的导电性质。
【课程讲授】提问：1.如何测绘伏安特性曲线？2.二极管导电有何特点？一、实验原理常用的晶体二极管是非线性电阻，其电阻值不仅与外加电压的大小有关，而且还与方向有关。
下面对它的结构和电学性能作一简单介绍。
图1线性电阻的伏安特性图2晶体二极管的p-n结和表示符号晶体二级管又叫半导体二极管。
半导体的导电性能介于导体和绝缘体之间。
如果在纯净的半导体中适当地掺入极微量的杂质，则半导体的导电能力就会有上百万倍的增加。
加到半导体中的杂质可分成两种类型：一种杂质加到半导体中去后，在半导体中会产生许多带负电的电子，这种半导体叫电子型半导体 (也叫n型半导体)；另一种杂质加到半导体中会产生许多缺少电子的空穴(空位)，这种半导体叫空穴型半导体 (也叫p型半导体)。
晶体二极管是由两种具有不同导电性能的n型半导体和p型半导体结合形成的p-n结构成的。
它有正、负两个电极，正极由p型半导体引出，负极由n型半导体引出，如图2(a)所示。
p-n结具有单向导电的特性，常用图2(b)所示的符号表示。
关于p-n结的形成和导电性能可作如下解释。
图3 p-n结的形成和单向导电特性如图3(a)所示，由于p区中空穴的浓度比n区大，空穴便由p区向n区扩散；同样，由于n区的电子浓度比p区大，电子便由p区扩散。
随着扩散的进行，p区空穴减少，出现了一层带负电的粒子区(以Ө表示)；n区的电子减少，出现了一层带正电的粒子区(以⊕表示)。
结果在p型与n型半导体交界面的两侧附近，形成了带正、负电的薄层，称为p-n结。
这个带电薄层内的正、负电荷产生了一个电场，其方向恰好与载流子(电子、空穴)扩散运动的方向相反，使载流子的扩散受到内电场的阻力作用，所以这个带电薄层又称为阻挡层。
广东第二师范学院学生实验报告院（系）名称班别姓名专业名称学号实验课程名称 电路与电子线路实验 实验项目名称 电路元件伏安特性的测绘 实验时间实验地点 实验成绩指导老师签名一、实验目的:(1) 学会识别常用电路元件的方法;(2) 掌握线性电阻、非线性电阻元件伏安特性的逐点测试法； (3) 掌握实验台上直流电工仪表和设备的使用方法.二、实验仪器： (1) 电路实验箱一台(2) 万用表一块,2AP9二极管一个，2CW51稳压管一个,不同阻值线性电阻器若干。
三、实验内容及步骤：1．测定线性电阻器的伏安特性按图3-3接线，调节稳压电源的输出电压U,从0V 开始缓慢地增加,一直到10V ，在表3—1记下相应的电压表和电流表的读数U R 和I 。
表3-1 测定线性电阻的伏安特性U R /V 0 1 2 3 4 5 6 7 8 9 10 I/mA1。
142.183。
224.275.226。
10 7。
128.139.1410。
162．测定半导体二极管的伏安特性按图3—4接线,R 为限流电阻器。
测二极管的正向特性时,其正向电流不得超过25mA ，二极管D 的正向压降U D+可在0~0.75V 之间取值。
在0.5～0.75V 之间应多取几个测量点.做反向特性实验的时候，只需将图1—3中的二极管D 反接，且其反向电压可加到30V 左右。
表3-2 测定二极管的正向特性U D+/V 0 0。
2 0.4 0。
45 0.5 0.55 0.60 0。
65 0.70 0。
75图3-4 二极管伏安特性测试 图3-3 线性电阻伏安特性测试I/mA 0 0 0.01 0.07 0.26 0.73 2。
05 6.03 17。
85 56.0表3-3 测定二极管的反向特性U D-/V 0 -5 -10 -15 -20 -25 -30I/mA 0 0 0—0.001-0。
001-0.002 -0.0023．测定稳压二极管的伏安特性(1)正向特性实验将图3-4中的二极管1N4007换成稳压二极管2CW51，重复实验内容2中的正向测量。
电阻定律欧姆定律伏安特性曲线一、基础知识(一)电阻、电阻定律1电阻U(1)定义式：R="p(2)物理意义：导体的电阻反映了导体对电流阻碍作用的大小.2、电阻定律：R= pS.3、电阻率(1)物理意义：反映导体导电性能的物理量，是导体材料本身的属性.(2)电阻率与温度的关系①金属的电阻率随温度升高而增—②半导体的电阻率随温度升高而减小_③超导体：当温度降低到绝对零度附近时，某些材料的电阻率突然减小为零，成为超导体.(二)部分电路欧姆定律1、内容：导体中的电流I跟导体两端的电压U成正比，跟导体的电阻R成反比.2、公式：I = U.R3、适用条件：适用于金属导体和电解质溶液导电，适用于纯电阻电路.(三)导体的伏安特性曲线1、导体的伏安特性曲线：用横坐标轴表示电压U，纵坐标轴表示电流I，画出的I —U关系图线.(1)线性元件：伏安特性曲线是通过坐标原点的直线的电学元件，适用于欧姆定律.(2)非线性元件：伏安特性曲线是曲线的电学元件，不适用于欧姆定律.2、I—U图象中的点表示“状态”点，该点与原点连线的斜率表示电阻的倒数相关的理解1、电阻与电阻率的区别(1)电阻是反映导体对电流阻碍作用大小的物理量，电阻大的导体对电流的阻碍作用大.电阻率是反映制作导体的材料导电性能好坏的物理量，电阻率小的材料导电性能好.⑵导体的电阻大，导体材料的导电性能不一定差；导体的电阻率小，电阻不一定小，即电阻率小的导体对电流的阻碍作用不一定小.⑶导体的电阻、电阻率均与温度有关.2、电阻的决定式和定义式的区别3、欧姆定律不同表达式的物理意义(1)1 =昔是欧姆定律的数学表达式，表示通过导体的电流I与电压U成正比，与电阻RR成反比.(2)公式R=半是电阻的定义式，它表明了一种测量电阻的方法，不能错误地认为“电阻跟电压成正比，跟电流成反比”.4、对伏安特性曲线的理解(1)图中，图线a、b表示线性元件，图线c、d表示非线性元件.(2)图象的斜率表示电阻的倒数，斜率越大，电阻越小，故R a<R b(如图5甲所示).(3)图线c的电阻减小，图线d的电阻增大(如图乙所示).甲乙⑷伏安特性曲线上每一点的电压坐标与电流坐标的比值对应这一状态下的电阻.（1）在I —U曲线上某点切线的斜率不是电阻的倒数.⑵要区分是I —U图线还是U —I图线.（3）对线性元件：R=学=罟；对非线性元件：R=学工罟•应注意，线性元件不同状态时比值不变，非线性元件不同状态时比值不同.二、练习1、导体的电阻是导体本身的一种性质，对于同种材料的导体，下列表述正确的是（）A •横截面积一定，电阻与导体的长度成正比B •长度一定，电阻与导体的横截面积成正比C •电压一定，电阻与通过导体的电流成正比D •电流一定，电阻与导体两端的电压成反比答案A解析对于同种材料的导体，电阻率是个定值，根据电阻定律R= &可知A对，B错.导体的电阻不随电流或电压的变化而变化.故C、D错.2、下列关于电阻率的说法中正确的是（）A •电阻率与导体的长度以及横截面积有关B •电阻率由导体的材料决定，且与温度有关C •电阻率大的导体，电阻一定大D •有些合金的电阻率几乎不受温度变化的影响，可用来制作电阻温度计答案B解析电阻率是反映材料导电性能的一个物理量，由导体的材料决定，且与温度有关，A错误，B 正确；决定电阻大小的除了电阻率以外，还要受导体的横截面积以及长度的影响，C错误；有些合金的电阻率几乎不受温度变化的影响，可以用来制作标准电阻，D错误.3、有一段长1 m的电阻丝，电阻是10 Q现把它均匀拉伸到长为5 m的电阻丝，则电阻变为（）A. 10 QB. 50 QC. 150 QD. 250 Q解析电阻丝无论怎样拉长其体积不变，但随着长度增加，截面面积减小，即满足V=1Sl关系式•把电阻丝由 1 m均匀拉伸到 5 m时，截面面积变成原来的1，由电阻定律R =P可知电阻变成原来的25倍，D正确.4、如图所示，在相距40 km的A、B两地架两条输电线，电阻共为800 Q,如果在A、B间的某处发生短路，这时接在A处的电压表示数为10 V，电流表示数为40 mA，求发生短路处距A处有多远.审题指导解析设发生短路处距A处为X,根据欧姆定律1= ¥可得：RA端到短路处的两根输电线的总电阻¥ 10R x= | = 2250 Q1 4 X 10-根据电阻定律可知：2xR x=PSA、B两地间输电线的总电阻为21R 总=Ps由②/③得R x xR总1解得x= R x i = frrx 40 km = 12.5 kmR 总800答案12.5 km5、一个内电阻可以忽略的电源，给一个绝缘的圆管子里装满的水银供电，电流为0.1 A，若把全部水银倒在一个内径大一倍的绝缘圆管子里，那么通过的电流将是（）2.0 A 和6.0 A ，把以上两根保险丝各取等长一段并联后再接入电路中，允许通过的 最大电流是答案 B电流I =丨1+ 12= 7.5 A .若h = 2 A ，贝U I 2= 8 A>6 A ，保险丝会熔断，故只有 B 正确.7、下列说法中正确的是（ ）A .由R = ■可知，电阻与电压、电流都有关系B .由R = &可知，电阻与导体的长度和横截面积都有关系C .各种材料的电阻率都与温度有关，金属的电阻率随温度的升高而减小D .所谓超导体，就是当其温度降低到接近绝对零度的某个临界温度时，它的电阻率突然变为零 答案 BD解析 R =半是电阻的定义式，R 与电压和电流无关，故 A 错误；而R = p 是电阻的决定 式，横截面积一定，电阻与导体的长度成正比，长度一定，电阻与导体的横截面积成反 比,故B 正确；电阻率都与温度有关，金属的电阻率随温度的升高而增大，故C 错误;当温度降低到接近绝对零度的某个临界温度时，导体的电阻率突然变为零的现象叫超导 现象，此时的导体叫超导体，故 D 正确.B . 0.8 AC . 1.6 A3.2 A答案 C解析 大圆管子内径大一倍，即横截面积为原来的4倍，由于水银体积不变，故水银高 1度变为原来的4，则由电阻定律知电阻变为原来的 116，由欧姆定律知电流变为原来的16倍. C 选项正确.6、甲、 乙两根保险丝均为同种材料制成，直径分别是d i = 0.5 mm 和d 2= 1 mm ，熔断电流分别为 A . 6.0 AB . 7.5 AC . 10.0 AD . 8.0 A解析 甲、乙保险丝等长，由电阻定律R = p 可知R =，所以 R 1 R 2= 4 1，把 R 1、nJR 2并联接入电路，由分流关系知 -=Z 2I 2 R 1因熔断电流12= 6 A ，故I i 只能是1.5 A ，总8、电位器是变阻器的一种•如图所示，如果把电位器与灯泡串联起来，利用它改变灯泡的亮度，下列说法正确的是（ ）A .串接A 、B 使滑动触头顺时针转动，灯泡变暗 B .串接A 、C 使滑动触头逆时针转动，灯泡变亮 C .串接A 、C 使滑动触头顺时针转动，灯泡变暗D .串接B 、C 使滑动触头顺时针转动，灯泡变亮解析 根据电位器结构和连线可知：串接A 、B 使滑动触头顺时针转动时回路电阻增大,回路电流减小，灯泡变暗， A 正确；同理，D 正确；串接A 、C 时，滑动触头不能改变 回路电阻，灯泡亮度不变，故B 、C 错误.9、根据部分电路欧姆定律，下列判断正确的有（）A .导体两端的电压越大，电阻就越大薄B .导体中的电流越大，电阻就越小C .比较几只电阻的I — U 图象可知，电流变化相同时，电压变化较小的图象是属于阻值 较大的那个电阻的D .由| = U 可知，通过一段导体的电流跟加在它两端的电压成正比R答案 D解析 导体的电阻表征导体阻碍电流的能力，由导体本身性质决定，与U 、丨无关，选项A 、B 错误；在电阻的I — U 图象中，阻值 R = fU ，当$相同时，AU 越小，表示该 导体的阻值越小，选项C 错误；根据欧姆定律1= ¥可知，通过一段导体的电流跟加在它R两端的电压成正比，跟导体的电阻成反比，选项D 正确.10、 如图所示是某导体的伏安特性曲线，由图可知正确的是（ ）A .导体的电阻是25 QB .导体的电阻是0.04 QC .当导体两端的电压是 10 V 时，通过导体的电流是 0.4 AD .当通过导体的电流是0.1 A 时，导体两端的电压是 2.5 V答案 ACD11、 如图所示是某导体的I — U 图线，图中a= 45 °下列说法正确的是（ ）A .通过电阻的电流与其两端的电压成正比答案 AD悄动触头 膜电阻000 A B CD 1020 UfyB .此导体的电阻R=2 QC . I —U图线的斜率表示电阻的倒数，所以R= cot 45 =1.0 Q答案 B14、小灯泡通电后其电流 I 随所加电压U 变化的图线如图所示， P 为图线上一点，PN 为图 线在P 点的切线，PQ 为U 轴的垂线，PM 为I 轴的垂线，则下列说法中错误的是（ ）A .随着所加电压的增大，小灯泡的电阻增大B .对应P 点，小灯泡的电阻为 R =严I 23.0 CD .在R 两端加6.0 V 电压时，每秒通过电阻截面的电荷量是答案 ABD解析 由题图可知，通过电阻的电流I 与其两端电压 U 成正比，A 正确；导体电阻R =彳 =2 0,对应I — U 图线斜率的倒数，但 R 丸ot 45 ； B 正确，C 错误；当U = 6.0 V 时，I =U= 3 A ，故每秒通过电阻截面的电荷量为 q = It = 3.0 C , D 正确.12、某导体中的电流随其两端电压的变化如图所示，则下列说法中正确的是A .力口 5 V 电压时，导体的电阻约是 5 0B .加11 V 电压时，导体的电阻约是1.4 0C •由图可知，随着电压的增大，导体的电阻不断减小D •由图可知，随着电压的减小，导体的电阻不断减小答案 AD解析 对某些导体，其伏安特性曲线不是直线，但曲线上某一点的学值仍表示该点所对应的电阻值.本题中给出的导体加 5 V 电压时，彳值为5,所以此时电阻为5 0, A 正确;当电压增大时，U ■值增大，即电阻增大，综合判断可知 B 、C 错误，D 正确.13、某一导体的伏安特性曲线如图中AB 段（曲线）所示，关于导体的电阻，以下说法正确的是（）A .B 点的电阻为12 0 B . B 点的电阻为40 0C •导体的电阻因温度的影响改变了 1 0D •导体的电阻因温度的影响改变了9 0解析根据电阻的定义式可以求出3A 、B 两点的电阻分别为 R A =乔 0= 30 0 R B =60.10= 40 0所以 AR = R B — R A = 10 0 故 B 对，A 、C 、D 错.3 fi UtND .对应P 点，小灯泡的功率为图中矩形PQOM 所围的面积答案 C解析 灯泡的电阻R = *，结合题图知，A 、B 正确，C 错误；小灯泡的功率 P = UI ，所 以D 正确.故选C.15、一只标有“ 220 V,60 W ”的白炽灯泡，加在其两端的电压 U 由零逐渐增大到 220 V ，在这一过程中，电压 U 和电流I 的关系与选项中所给的四种情况比较符合的是（）答案 B解析 灯泡两端电压逐渐增大的过程，灯丝的温度升高，灯丝的电阻变大，则U — I 图线的斜率变大，结合所给 U - I 图线可知B 对，A 图线斜率不变，不对； C 图线斜率变 小，不对；D 图线斜率先变大后变小，不对.16、酒精测试仪的工作原理如图所示，其中 P 是半导体型酒精气体传感器，该传感器电阻 r '的倒数与酒精气体的浓度 c 成正比,1的倒数Q 之间关系的图象，正确的是答案 A C .对应P 点，小灯泡的电阻为R=U i I 2—R o 为定值电阻•以下关于电压表示数的倒数与酒精气体浓度解析由题意设k r由部分电路的欧姆定律可得 U = IR o = 1 R o + r 、，整理为U =ER oAioR o + r 击 R o + r r ' R o + r k1―ER0 — = ER o + ER^= ER 0 +ERL •，结合数学知识可知 A 选项正确.17、在如图所示电路中， AB 为粗细均匀、长为 L的电阻丝，以 A 、B则U 随x 变化的图线应为利用“柱体微元”模型求解电流的微观表达式问题粗细均匀的一段导体长为I ，横截面积为s ,导体单位体积内的自由电荷数为 n ,每个自由电荷的电荷量为 q ,当导体两端加上一定的电压时，导体中的自由电荷沿导体定向移 动的速率为v ，则(1) 导体内的总电荷量： Q = nISq. (2) 电荷通过导体截面的时间： t = ~. (3)电流的微观表达式：1 =半=nqSv.18、截面积为S 的导线中通有电流I•已知导线每单位体积中有数是解析因为I=AAt ，所以q=I•鸟自由电子数为：N =：=兰，则 选项C 正确.又因为电流的微观表达式为 I = nevS ,上各点相对A 点的电压为纵坐标，各点离 答案 A解析由U = IR x =E- RRLL fx ,其中E 、L 均为定值，故 U 与x 成正比.A 项正确.的电荷量是e ,自由电子定向移动的速率是v ,则在时间 At 内通过导线截面的自由电子n 个自由电子，每个自由电子A . nSv AtB. nvAtI At C.；D.LAt SeA 点的距离x 为横坐标,UD所以自由电子数为N = e =冒=呼=，选项A 正确• “柱体微元”模型求解问题•力学中即取一段空气柱作为研究对象.19、如图所示，一根横截面积为S 的均匀长直橡胶棒上均匀带有负电荷， 设棒单位长度内所含的电荷量为q ，当此棒沿轴线方向做速度为 v 的匀速直线运动时，由于棒的运动而形成的 等效电流大小为( )------- pqqv J 99000000A . qvB. vC . qvS答案 A解析 在垂直棒的运动方向选取一截面，设棒长为I ，则棒上所有电荷通过这一截面所用的时间t =-，由电流的定义式1= q,可得：1 =弓=qv.v t丄v我们常利用此模型解请同学们自己推导一下.答案 AC。
