信号与系统答案(刘卫东)第八章

《信号与系统》课后习题参考答案第二章 连续信号与系统的时域分析2-9、（1）解：∵系统的微分方程为：)(2)(3)(t e t r t r '=+'，∴r(t)的阶数与e(t) 的阶数相等，则h(t)应包含一个)(t δ项。

又∵系统的特征方程为：03=+α，∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程（此时e(t)= )(t δ），得：)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。

∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。

2-11、解：①求)(t r zi ： ∵系统的特征方程为：0)3)(2(652=++=++αααα，∴特征根：21-=α，32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs ：t t e A eA t h 3221)(--+= (t ≥0)，可求得：11=A ，12-=A （求解过程略） ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r ：)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=，21=C 21=C ∴ 011=-C ， ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi ， ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解：（1）依题意，得：)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---，两边求导得：)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ （2）∵系统的起始状态保持不变，∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+，∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证：∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时：u(t-3k)为非零值 又∵0≤t ≤3，∴k 取负整数，则：3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(，且311--=e A 。

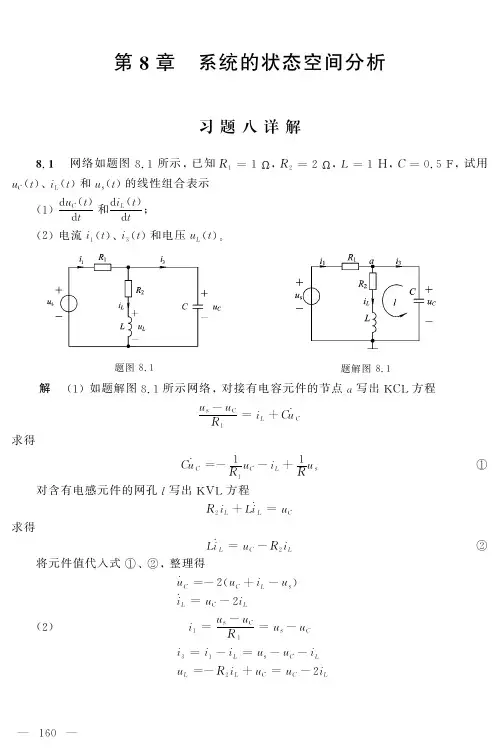
第八章习题8.1 图示一反馈系统，写出其状态方程和输出方程。

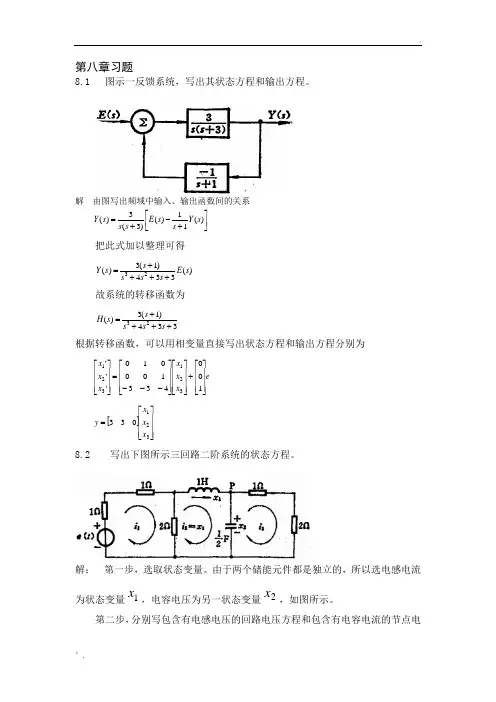
解由图写出频域中输入、输出函数间的关系⎥⎦⎤⎢⎣⎡+-+=)(11)()3(3)(sYssEsssY把此式加以整理可得)(334)1(3)(23sEsssssY++++=故系统的转移函数为334)1(3)(23++++=sssssH根据转移函数，可以用相变量直接写出状态方程和输出方程分别为exxxxxx⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡143311'''321321[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=32133xxxy8.2 写出下图所示三回路二阶系统的状态方程。

解：第一步，选取状态变量。

由于两个储能元件都是独立的，所以选电感电流为状态变量1x，电容电压为另一状态变量2x，如图所示。

第二步，分别写包含有电感电压的回路电压方程和包含有电容电流的节点电流方程。

根据第二个回路的回路方程，并代入元件参数，则有112122'ixxx+--=312'21ixx-=第三步，上两式中1i和3i不是状态变量，要把它们表为状态变量。

由第一个回路有1124xie-=，即112141xei+=由第三个回路有323ix=，即2331xi=把1i和3i分别代入第二步中两式，并经整理，最后得所求状态方程为exxx21'211+--=212322'xxx-=或记成矩阵形式8.3 图示一小信号谐振放大器的等效电路，这里的激励函数)(t e是一压控电流源，输出电压)(t y由耦合电路的电阻L R上取得。

要求写出此电路的状态方程和输出方程。

解：第一步，选状态变量。

因为电感电流和电容电压等三个变量都是独立的，所以选回路电感L中的电流1x、回路电容C上的电压2x、耦合电容c C上的电压3x为状态变量。

第二步，分别写回路方程或节点方程。

由RLC回路有211'xRxLx=+eixxCCx rc-=+++132''RL c i x C ='3第三步，消去非状态变量。

第一章习题参考解答1.1 绘出下列函数波形草图。

(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t tx επ= (5) )]4()([4cos )(--=-t t t et x tεεπ(7) t t t t x 2cos)]2()([)(πδδ--=(9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率，并指出是能量信号还是功率信号，或两者均不是。

(1) ||3)(t et x -=解 能量有限信号。

信号能量为：(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。

信号能量为：(3) t t x π2sin )(=解 功率有限信号。

周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率，t π2sin 的周期为1。

(4) n n x 4sin)(π=解 功率有限信号。

n 4sin π是周期序列，周期为8。

(5) )(2sin )(t t t x επ=解 功率有限信号。

由题(3)知，在),(∞-∞区间上t π2sin 的功率为1/2，因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。

如果考察)(2sin t t επ在),0(∞区间上的功率，其功率为1/2。

(6) )(4sin)(n n n x επ=解 功率有限信号。

由题(4)知，在),(∞-∞区间上n 4sin π的功率为1/2，因此)(4sinn n επ在),(∞-∞区间上的功率为1/4。

如果考察)(4sinn n επ在),0(∞区间上的功率，其功率为1/2。

第6章 系统及系统的时域分析1. 解：由于系统(1)不满足分解性；系统(2)不满足零输入线性；系统(3)不满足零状态线性，故这三个系统都不是线性系统。

对于系统(4)，如果直接观察)(n y ～)(n f 关系，似乎系统既不满足齐次性，也不满足叠加性。

但考虑到令)(n f =0时，系统响应为常数b ，若把它看成是由初始状态引起的零输入响应时，系统仍是满足线性系统条件的，故系统(4)是线性系统。

2. 解：(1) 已知)(t f →)](cos[)(t f a t y f =，设 dd t t t t f t f >-=),()(1，则其零状态响应为)](cos[)](cos[)(11d f t t f a t f a t y -==，显然 )()(1d f f t t y t y -=，故该系统是时不变系统。

(2) 已知)(n f →)()(n bf n y f =，设01),()(n n n n f n f >-=，则其零状态响应为)()()(011n n bf n bf n y f -==，显然 )()(01n n y n y f f -=，故该系统是时不变系统。

3. 解：对于（1）～（4），由于任一时刻的零状态响应均与该时刻以后的输入无关，因此都是因果系统。

而对于（5），系统任一时刻的零状态响应都与该时刻以后的激励有关。

响应在先，激励在后，这在物理系统中是不可能的。

因此，该系统是非因果的。

（6）也是非因果的，因为如果0)(=t f ，0t t < 则有 0)3()(==t f t y f ，3t t <可见在区间003t t t <<上0)(≠t y f ，即零状态出现于激励之前，因而该系统是非因果的。

4. 解：（1）显然，无论激励)(n f 是何种形式的序列，只要它是有界的，那么)(n y f 也是有界的，因果该系统是稳定的。

（2）若)()(t u t f =，显然该激励是有界的，但 t x x u t y tf ==⎰∞-d )()(，0≥t它随时间t 无限增长，故该系统是不稳定的。

信号与系统前三章习题答案信号与系统前三章习题答案第一章：信号与系统基础1.1 习题答案1. 信号是指随时间变化的物理量，可以用数学函数表示。

系统是指对输入信号进行处理或变换的过程或装置。

2. 信号可以分为连续时间信号和离散时间信号。

连续时间信号在每个时间点上都有定义，可以用连续函数表示；离散时间信号只在某些离散的时间点上有定义，可以用数列表示。

3. 周期信号是在一定时间间隔内重复的信号，非周期信号则不具有重复性。

周期信号可以用正弦函数或复指数函数表示。

4. 信号的能量是指信号在无穷远处的总能量，可以用积分的形式表示；信号的功率是指信号在某个时间段内的平均功率，可以用平均值的形式表示。

5. 系统的特性可以通过冲激响应和频率响应来描述。

冲激响应是指系统对单位冲激信号的响应，可以用单位冲激函数表示；频率响应是指系统对不同频率信号的响应，可以用频率函数表示。

1.2 习题答案1. 线性系统具有叠加性和齐次性。

叠加性是指系统对两个输入信号的响应等于两个输入信号分别经过系统的响应的叠加；齐次性是指系统对输入信号的线性组合的响应等于输入信号分别经过系统的响应的线性组合。

2. 时不变性是指系统的特性不随时间的变化而变化。

即如果输入信号发生时间平移，系统的响应也会相应地发生时间平移。

3. 因果性是指系统的输出只依赖于当前和过去的输入信号。

即系统的响应不会提前预知未来的输入信号。

4. 稳定性是指系统对有界输入信号产生有界输出信号。

即输入信号有限，输出信号也有限。

5. 可逆性是指系统的输出可以唯一确定输入。

即系统的响应函数是可逆的。

第二章：连续时间信号与系统2.1 习题答案1. 连续时间信号的频谱是指信号在频域上的表示，可以通过傅里叶变换得到。

频谱表示了信号在不同频率上的能量分布情况。

2. 系统的冲激响应可以通过输入信号和输出信号的傅里叶变换来求得。

通过傅里叶变换，可以将系统的时域特性转换为频域特性。

3. 傅里叶变换具有线性性、时移性、频移性和共轭对称性。

信号与系统课后习题参考答案1试分别指出以下波形就是属于哪种信号？题图1-11-2试写出题1-1图中信号得函数表达式。

1-3已知信号与波形如题图1-3中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-3⑴⑵⑶⑷⑸⑹⑺⑻⑼1-4已知信号与波形如题图1-4中所⽰,试作出下列各信号得波形图,并加以标注。

题图1-4⑴⑵⑶⑷⑸⑹⑺⑻⑼1-5已知信号得波形如题图1-5所⽰,试作出信号得波形图,并加以标注。

题图1-51-6试画出下列信号得波形图:⑴⑵⑶⑷1-7试画出下列信号得波形图:⑴⑵⑶⑷⑸⑹1-8试求出以下复变函数得模与幅⾓,并画出模与幅⾓得波形图。

⑴⑵⑶⑷1-9已知信号,求出下列信号,并画出它们得波形图。

1-10试作出下列波形得奇分量、偶分量与⾮零区间上得平均分量与交流分量。

题图1-101-11试求下列积分:⑴⑵⑶⑷⑸⑹1-12试求下列积分:⑴⑵⑴(均为常数)⑵⑶⑷⑸⑹⑺⑻1-14如题图1-14中已知⼀线性时不变系统当输⼊为时,响应为。

试做出当输⼊为时,响应得波形图。

题图1-14 1-15已知系统得信号流图如下,试写出各⾃系统得输⼊输出⽅程。

题图1-151-16已知系统⽅程如下,试分别画出她们得系统模拟框图。

⑴⑵⑶1-17已知⼀线性时不变系统⽆起始储能,当输⼊信号时,响应,试求出输⼊分别为与时得系统响应。

第⼆章习题2-1试计算下列各对信号得卷积积分:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-2试计算下列各对信号得卷积与:。

⑴(对与两种情况)⑵⑶⑷⑸⑹2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。

题图2-32-4试计算下图中各对信号得卷积与:,并作出结果得图形。

题图2-42-5已知,试求:⑴⑵⑶2-7系统如题图2-7所⽰,试求系统得单位冲激响应。

已知其中各⼦系统得单位冲激响应分别为:题图2-72-8设已知LTI 系统得单位冲激响应,试求在激励作⽤下得零状态响应。

2-9⼀LTI 系统如题图2-9所⽰,由三个因果LTI ⼦系统级联⽽成,且已知系统得单位样值响应如图中。

信号与系统课后答案第1章1-1题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解(a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。

1-2给定题1-2图示信号f ( t )，试画出下列信号的波形。

[提示：f ( 2t )表示将f ( t )波形压缩，f (2t)表示将f ( t )波形展宽。

](a) 2f (t - 2 ) (b) f ( 2t )(c)f (2t )(d)f (-t +1 ) 题1-2图解以上各函数的波形如图p1-2所示。

图p1-21-3如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图解各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i C t u ττd )(1)(S RS L S C1-4如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

题1-4图解系统为反馈联接形式。

设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) +f 2( t )，则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。

《信号与系统》习题参考答案（1）2—1（1） 01()()()()(1)()ta at x t h t x u t d e d e u t aτττττ∞---∞*=⋅-==-⎰⎰ （2） 00()()(cos sin )()x t h t t d ωτωτδττ∞-∞*=+⋅-⎰0000(cos sin )()cos sin t t t d t t ωωδττωω∞-∞=+⋅-=+⎰（3） 当0t <时 ()()0x t h t *=当01t ≤<时 20()()(1)2tt x t h t d t ττ*=+=+⎰当12t ≤<时 13()()(1)2x t h t d ττ*=+=⎰ 当23t ≤<时 12213()()(1)22t x t h t d t t ττ-*=+=-++⎰ 当3t ≥时 ()()0x t h t *= （4） 当0t <时 ()()0x t h t *=当0t ≥时 01()()sin 2(1cos 2)2tx t h t d t ττ*==-⎰ （5） 22222(2)2(4)241()()(2)2t t t t t t t x t h t e d e d e ee ττττ-----*=-=-+⎰⎰ （6）()x t at b =+11212()()()()()(2)3363tt x t h t a b d a tb t a t a bττδ-*=+++*--=++⎰2—2（1） [][][][2](2)[2]x n h n nu n n n u n δ*=*-=--（2） 10[][](2)[](21)[]nin i x n h n u n u n +=*==-∑（3） 当0n ≥时 1111[][]2()()232i n in i x n h n --=-∞*==∑ 当0n <时 111[][]2()223n i n i n i x n h n --=-∞*==⋅∑ （4） 当0n <时 [][]0x n h n *=当0n ≥时 110[][]()[]n n nin ii x n h n u n βααββα++-=-*==-∑（5） 当07n ≤≤时 071[][](1)[1(1)]2in i n x n h n -=-*=-=--∑ 当70n -≤≤时 71[][](1)[(1)1]2ni n i x n h n -=-*=-=--∑ 2—3（1） 12()()[(1)(1)][(5)(5)]x t x t u t u t t t δδ*=+--*++- (6)(4)(4)(6)u t u t u t u t =++--+-- （2） 123()()()x t x t x t **{[(6)(4)][(4)(6)]}*[u t u t u t u t =+-++---11()()]22t t δδ++- ( 6.5)( 4.5)( 5.5)( 3.5)( 3.5)( 5.5)u t u t u t u t u t u t =+-+++-++--- ( 4.5)( 6.5)u t u t +---（3） 1311()()[(1)(1)][()()]22x t x t u t u t t t δδ*=+--*++- ( 1.5)(0.5)(0.5)( 1.5)u t u t u t u t =+--++-- 2—4 0(3)331()(3)1t k k t tk k y t eu t k e e e e∞-----=-∞=-∞=-=⋅=-∑∑311A e-=- 2—5（1） 当2t ≥时 ()()0x t h t *= 当20t -<<时 11()()2t x t h t d t τ+-*==+⎰当02t <<时 11()()2t x t h t d t τ-*==-⎰（2） 当01t <<时 1()()22(1)tx t h t d t τ*==-⎰ 当10t -<<时 01()()22(1)2t tx t h t d d t t t ττ+*=+=-++=+⎰⎰当21t -<<-时 11()()2t x t h t d t τ+-*==+⎰当 1t ≥ 或 2t <-时 ()()0x t h t *=此题也可利用性质，先对()x t 积分，对()h t 微分，'()()()y t x t dt h t =*⎰（3） 当0t <时 (1)1()()1t x t h t e dt +∞--*==⎰当0t ≥时 1(1)(1)11()()22t t t t t x t h t e dt e dt e ++∞-----+*=+=-⎰⎰（4） 当t π< 或 5t π>时 ()()0x t h t *= 当3t ππ<<时 0()()sin 1cos t x t h t d t πττ-*==+⎰当35t ππ<<时 23()()sin 1cos t x t h t d t ππττ-*==--⎰（5） 当01t <<时 2211()()222()22x t h t t t t *=-=--当12t <≤时 2231()()264[2()]22x t h t t t t *=-+-=---()()x t h t *是以2为周期的周期函数 2—7（1） 111[][1]()[]()[1]22nn h n Ah n u n A u n ---=--111()[()()][1]()22nn n A u n n δδ-=+--=12A =（2） 111[][][][1][][]h n h n Ah n h n h n n δ---*-*-=*11[][][1]2h n n n δδ-∴=-- （3） 11[][][]2[[][1]][]nx n h n h n u n u n h n --**=--* 2[]2[[][4]]2[[1][5]]nn x n u n u n u n u n -∴=------2—8（1） 0()3()y t y t =（2） 00()()(2)y t y t y t =-- （3） 0()(1)y t y t =- （4） 0()()y t y t =-（5） 0()()dy t y t dt=（6） 202()()d y t y t dt =2—9 12111[][]()[]()[1]222n n x n h n u n u n -*=-+--1()([][1])[]2nu n u n n δ=---=1221[][][][]([][])*[]y n x n h n h n x n h n h n =**=* []*([][])[][]n n n n n u n u n u n u n δαβαβ=+=+ 2—10（1） 341201[][]((0.5))[3]2(1())[3]2n nn n x n x n u n u n ++=*=+=-+∑ （2） 4123[][][]2(1(0.5))[3]([][1])n x n x n x n u n n n δδ+**=-+*-- 43312(1(0.5))[3]2(1(0.5))[2]()[3]2n n n u n u n u n +++=-+--+=+ （3） 23[][][3]([][1])[3][2][3]x n x n u n n n u n u n n δδδ*=+*--=+-+=+ 2—11（1） 12345[][]([][][])[]h n h n h n h n h n h n =*-*+ （2） 34[][][1]h n h n nu n *=- 234[][][](1)[][1][]h n h n h nn u n n u n u n -*=+--= 12345[][]([][][])[]h n h n h n h n h n h n =*-*+514()([][3])*[][]2nu n u n u n hn =--+ 4[]6[1]7[2][]4[3]5[]6[1]7[2]4[3]n n u n n n n n u n n δδδδδδδ=+-+-++-=+-+---（1）'()()(2)(2)()(2)tt y t e x d x t y t x t τττ---∞=--+-=-+-⎰(2)()(2)t h t eu t --=- （2）当1t ≤时 ()0y t =当14t <≤时 1(2)(1)2()1t t y t e d e ττ+----==-⎰当4t >时 1(2)(4)(1)2()t t t t y t e d e e ττ+-------==-⎰2—13（1）213()()()()(1)[()](1)[()](1)h t h t h t u t t t u t t u t δδδ**=*-*-=-*-=-- 1213()()()()()()(1)h t h t h t h t h t u t u t =+**=--（2）1(10)1(02)()3(23)0t t t y t t t +-<<⎧⎪<<⎪=⎨-<<⎪⎪⎩其余2—14（1）因果、稳定 （2）非因果、非稳定 （3）非因果、稳定 （4）非因果、稳定 （5）非因果、稳定 （6）因果、稳定 （7）因果、非稳定 2—15（1）因果、稳定 （2）非因果、稳定 （3）非因果、非稳定 （4）非因果、稳定 （5）因果、非稳定 （6）非因果、稳定 （7）因果、稳定 2—16（1）对 （2）对()h t dt ∞-∞=+∞⎰（3）错 例如单位冲激响应(1)t δ-是因果的，但LTI 系统的逆系统(1)t δ+不是因果的。

《信号与系统》第1~8章习题参考解答第一章 (2)第二章 (13)第三章 (22)第四章 (35)第五章 (48)第六章（无） (56)第七章 (57)第八章 (65)第一章1-4 对于例1-1所示信号，由f (t )求f (−3t − 2)，但改变运算顺序，先求f (3t )或先求f (−t )，讨论所得结果是否与原例之结果一致。

解：(1). 例1-1的方法： f (t )→ f (t − 2)→ f (3t − 2)→ f (−3t − 2) (2). 方法二：f (t )→ f (3t )→ 2[3()]3f t − →f (−3t − 2) (3). 方法三：f (t )→f (−t ) →[(2)]f t −+ →f (−3t − 2)方法三：1-5 已知()f t ，为求0()f t at −应按下列哪种运算求得正确结果（式中0t ，a 都为正值）？（1）()f at −左移0t （2）()f at 右移0t （3）()f at 左移0t a （4）()f at −右移0ta解：（4）()f at −右移t a：故（4）运算可以得到正确结果。

注：1-4、1-5 题考察信号时域运算：1-4 题说明采用不同的运算次序可以得到一致的结果； 1-5 题提醒所有的运算是针对自变量t 进行的。

如果先进行尺度变换或者反转变换，再进行移位变换，一定要注意移位量和移位的方向。

1-9 粗略绘出下列各函数式的波形图： （1）()(2)()t f t e u t −=− （2）2()(36)()t t f t e e u t −−=+ （3）3()(55)()t t f t e e u t −−=−（4）()cos(10)[(1)(2)]t f t e t u t u t π−=−−− 解：（1）()(2)()tf t e u t −=−（2）2()(36)()ttf t e eu t −−=+（3）3()(55)()ttf t e eu t −−=−（4）()cos(10)[(1)(2)]tf t e t u t u t π−=−−−1-12 绘出下列各时间函数的波形图，注意它们的区别：（1）[()(1)]−−；t u t u t（2）(1)�；t u t−（3）[()(1)](1)−−+−；t u t u t u t（4）(1)(1)−−；t u t（5）(1)[()(1)]−−−−；t u t u t（6）[(2)(3)]−−−；t u t u t（7）(2)[(2)(3)]t u t u t−−−−。