信号与系统课后答案

1试分别指出以下波形是属于哪种信号？题图1-11-2 试写出题1-1 图中信号的函数表达式。

1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示，试作出下列各信号的波形图，并加以标注。

题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。

题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示，试作出信号x(t)的波形图，并加以标注。

题图1-51- 6 试画出下列信号的波形图：1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图：⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角，并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。

题图 1-10形图。

题图 1-141-15 已知系统的信号流图如下，试写出各自系统的输入输出方程。

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD （15,6）=3 Hz 。

因此，公共周期3110==f T s 。

(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD （5, 15）=5 Hz 。

因此，公共周期5110==f T s 。

(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数，因此无法找出公共周期。

所以是非周期的。

(d) 两个分量是同频率的，基频 =0f 1/π Hz 。

因此，公共周期π==01f T s 。

1-2 解 (a) 波形如图1-2(a)所示。

显然是功率信号。

t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。

显然是能量信号。

3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号，显然有 1=P W1-3 解 周期T=7 ，一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+； (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。

1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。

《低频电子线路》一、单选题（每题2分，共28分：双号做双号题，单号做单号题）1.若给PN结两端加正向电压时，空间电荷区将（）A变窄B基本不变C变宽D无法确定2.设二极管的端电压为 U，则二极管的电流与电压之间是（）A正比例关系B对数关系C指数关系D无关系3.稳压管的稳压区是其工作（）A正向导通B反向截止C反向击穿D反向导通4.当晶体管工作在饱和区时，发射结电压和集电结电压应为 ( ) A前者反偏，后者也反偏B前者反偏，后者正偏C前者正偏，后者反偏D前者正偏，后者也正偏5.在本征半导体中加入何种元素可形成N型半导体。

（）A五价B四价C三价D六价6.加入何种元素可形成P 型半导体。

（）A五价B四价C三价D六价7.当温度升高时，二极管的反向饱和电流将（）。

A 增大B 不变C 减小D 不受温度影响8. 稳压二极管两端的电压必须（ ）它的稳压值Uz 才有导通电流，否则处于截止状态。

A 等于B 大于C 小于D 与Uz 无关9. 用直流电压表测得放大电路中某三极管各极电位分别是2V 、6V 、2.7V ，则三个电极分别是（） A （B 、C 、E ）B （C 、B 、E ）C （E 、C 、B ）D （B 、C 、E ）10. 三极管的反向电流I CBO 是由（ ）形成的。

A 多数载流子的扩散运动B 少数载流子的漂移运动C 多数载流子的漂移运动D 少数载流子的扩散运动11. 晶体三极管工作在饱和状态时，集电极电流C i 将（ ）。

A 随B i 增加而增加B 随B i 增加而减少C 与B i 无关，只决定于e R 和CE uD 不变12. 理想二极管的正向电阻为( )A A.零 B.无穷大 C.约几千欧 D.约几十欧13. 放大器的输入电阻高，表明其放大微弱信号能力（ ）。

A 强B 弱C 一般D 不一定14. 某两级放大电路，第一级电压放大倍数为5，第二级电压放大倍数为20，该放大电路的放大倍数为（ ）。

A 100B25C 5D2015.如题47图所示电路中，静态时， T1、T2 晶体管发射极电位UEQ为( ) 。

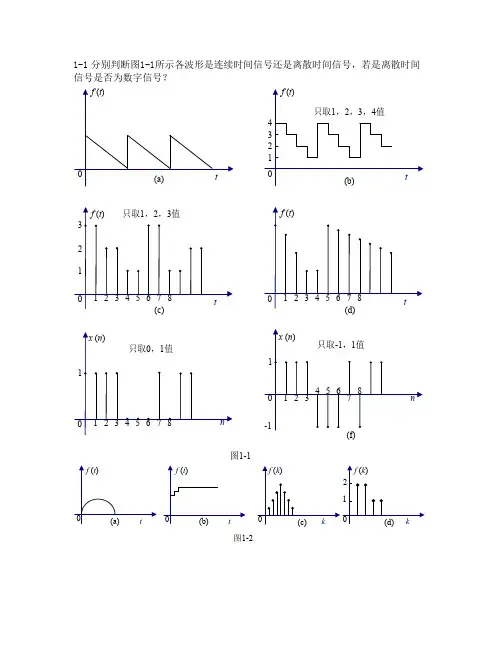
1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？图1-1图1-2解 信号分类如下：图1-1所示信号分别为⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--））（散（例见图数字：幅值、时间均离））（连续（例见图抽样：时间离散，幅值离散））（连续（例见图量化：幅值离散，时间））（续（例见图模拟：幅值、时间均连连续信号d 21c 21b 21a 21（a ）连续信号（模拟信号）；（b ）连续（量化）信号；（c ）离散信号，数字信号；（d ）离散信号；（e ）离散信号，数字信号；（f ）离散信号，数字信号。

1-2 分别判断下列各函数式属于何种信号？（重复1-1题所示问）（1）；)sin(t e at ω-（2）；nT e -（3）；)cos(πn （4）；为任意值）（00)sin(ωωn （5）。

221⎪⎭⎫ ⎝⎛解由1-1题的分析可知：（1）连续信号；（2）离散信号；（3）离散信号，数字信号；（4）离散信号；（5）离散信号。

1-3 分别求下列各周期信号的周期T ：（1）；)30t (cos )10t (cos -（2）；j10t e （3）；2)]8t (5sin [（4）。

[]为整数）（n )T nT t (u )nT t (u )1(0n n ∑∞=-----解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号，需要考察各分量信号的周期是否存在公倍数，若存在，则该复合信号的周期极为此公倍数；若不存在，则该复合信号为非周期信号。

（1）对于分量cos (10t )其周期；对于分量cos (30t )，其周期。

由于5T 1π=15T 2π=为的最小公倍数，所以此信号的周期。

5π21T T 、5T π=（2）由欧拉公式)t (jsin )t (cos e t j ωωω+=即)10t (jsin )10t (cos e j10t +=得周期。

5102T ππ==（3）因为[])16t (cos 2252252)16t (cos 125)8t (5sin 2-=-⨯=所以周期。

绪论单元测试1【判断题】(1分)本课程涉及的三大变换是傅里叶变换、拉普拉斯变换、z变换A.对B.错第一章测试1【单选题】(5分)信号是()信号A.离散周期信号B.连续周期信号C.离散非周期信号D.连续非周期信号2【单选题】(5分)序列是否为周期序列，若是周期序列，其周期N为A.是，N=3B.是，N=4C.不是D.是，N=83【判断题】(5分)线性时不变系统一定是稳定的系统A.对B.错4【判断题】(5分)线性系统一定是因果系统A.对B.错5【判断题】(5分)线性系统可以是时变系统，也可以是时不变系统A.错B.对6【判断题】(5分)因果系统一定是稳定的系统A.错B.对7【判断题】(5分)两个连续周期信号之和仍为周期信号A.对B.错8【单选题】(5分)试判断序列是否是周期序列，如果是，周期N=？A.是，N=12B.不是周期序列C.是，N=24D.是，N=89【单选题】(5分)已知信号f(t)的波形如下图所示，则f(6-2t)的波形图为A.B.C.D.10【单选题】(5分)f(3-3t)是如下()运算的结果A.f(-3t)右移1B.f(3t)右移1C.f(3t)左移1D.f(-3t)左移111【单选题】(5分)信号f(t)=2ε(t+1)-3ε(t-1)+ε(t-2)的波形图为A.B.C.D.12【单选题】(5分)下图所示序列f(k)闭合表示式为A.f(k)=ε(k-3)-ε(k-6)B.f(k)=ε(k-3)-ε(k-7)C.f(k)=ε(k-2)-ε(k-6)D.f(k)=ε(k-2)-ε(k-7)13【单选题】(5分)A. 2B.1C.D.314【单选题】(5分)已知f(t)的波形如下图所示，则f(t)的表达式为A.f(t)=(t+1)ε(t)-(t+1)ε(t+1)B.f(t)=(1-t)ε(t)-(1-t)ε(t-1)C.f(t)=tε(t)-(t-1)ε(t-1)D.f(t)=tε(t)-tε(t-1)15【单选题】(5分)系统为为（）系统。

3-1 求图3-1所示对称周期矩形信号的傅利叶级数〔三角形式和指数形式〕。

图3-1解 由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数〔FS 〕为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数〔FS 〕的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。

假设：图3-22T-2-重复频率kHz f 5= 脉宽s μτ20=幅度V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。

解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数〔FS 〕的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n那么的指数形式的傅利叶级数〔FS 〕为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 假设周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：〔1〕)(1t f 的谱线间隔和带宽〔第一零点位置〕，频率单位以kHz 表示； 〔2〕)(2t f 的谱线间隔和带宽； 〔3〕)(1t f 与)(2t f 的基波幅度之比； 〔4〕)(1t f 基波与)(2t f 三次谐波幅度之比。

第一章1.3 解：(a). 2401lim(),04Tt T TE x t dt e dt P ∞-∞∞→∞-====⎰⎰(b) dt t x TP T TT ⎰-∞→∞=2)(21lim121lim ==⎰-∞→dt T TTT∞===⎰⎰∞∞--∞→∞dt t x dt t x E TTT 22)()(lim(c).222lim()cos (),111cos(2)1lim()lim2222TT TTTT T TTE x t dt t dt t P x t dt dt TT∞∞→∞--∞∞→∞→∞--===∞+===⎰⎰⎰⎰(d) 034121lim )21(121lim ][121lim 022=⋅+=+=+=∞→=∞→-=∞→∞∑∑N N n x N P N Nn n N N N n N 34)21()(lim202===∑∑-∞=∞→∞nNNn N n x E (e). 2()1,x n E ∞==∞211lim []lim 112121N NN N n N n NP x n N N ∞→∞→∞=-=-===++∑∑ (f) ∑-=∞→∞=+=NNn N n x N P 21)(121lim 2∑-=∞→∞∞===NNn N n x E 2)(lim1.9. a). 00210,105T ππω===; b) 非周期的； c) 00007,,22mN N ωωππ=== d). 010;N = e). 非周期的； 1.12 解：∑∞=--3)1(k k n δ对于4n ≥时，为1即4≥n 时，x(n)为0，其余n 值时，x(n)为1易有：)3()(+-=n u n x , 01,3;M n =-=- 1.15 解：(a)]3[21]2[][][222-+-==n x n x n y n y , 又2111()()2()4(1)x n y n x n x n ==+-， 1111()2[2]4[3][3]2[4]y n x n x n x n x n ∴=-+-+-+-，1()()x n x n = ()2[2]5[3]2[4]y n x n x n x n =-+-+- 其中][n x 为系统输入。

1-4 分析过程：（1）例1-1的方法：()()()()23232f t f t f t f t →−→−→−− （2）方法二：()()()233323f t f t f t f t ⎡⎤⎛⎞→→−→−−⎜⎟⎢⎥⎝⎠⎣⎦（3）方法三：()()()()232f t f t f t f t →−→−+→−−⎡⎤⎣⎦ 解题过程：（1）方法一：方法二：（1）()−f at 左移0t ：()()()000−+=−−≠−⎡⎤⎣⎦f a t t f at at f t at （2）()f at 右移0t ：()()()000−=−≠−⎡⎤⎣⎦f a t t f at at f t at （3）()f at 左移0t a ：()()000⎡⎤⎛⎞+=+≠−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a （4）()f at 右移0t a ：()()000⎡⎤⎛⎞−−=−+=−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a 故（4）运算可以得到正确结果。

注：1-4、1-5题考察信号时域运算：1-4题说明采用不同的运算次序可以得到一致的结果；1-5题提醒所有的运算是针对自变量t 进行的。

如果先进行尺度变换或者反转变换，再进行移位变换，一定要注意移位量和移位的方向。

1-9 解题过程： （1）()()()2tf t eu t −=− （2）()()()232tt f t ee u t −−=+（3）()()()255ttf t e eu t −−=− （4）()()()()cos 1012tf t et u t u t π−=−−−⎡⎤⎣⎦1-12 解题过程：（（（（注：1-9、1-12题中的时域信号均为实因果信号，即()()()=f t f t u t 1-18 分析过程：任何信号均可分解为奇分量与偶分量之和的形式，即()()()()1e o f t f t f t =+其中，()e f t 为偶分量，()o f t 为奇分量，二者性质如下：()()()()()()23e e o o f t f t f t f t =−=−−()()13∼式联立得()()()12e f t f t f t =+−⎡⎤⎣⎦ ()()()12o f t f t f t =−−⎡⎤⎣⎦ 解题过程：(a-1) (a-2)(a-3)(a-4)f t为偶函数，故只有偶分量，为其本身(b) ()(c-1)(c-2)(c-3)(c-4)(d-1)(d-2)(d-3)(d-4)1-20 分析过程：本题为判断系统性质：线性、时不变性、因果性（1）线性（Linearity）：基本含义为叠加性和均匀性即输入()1x t ，()2x t 得到的输出分别为()1y t ，()2y t ，()()11T x t y t =⎡⎤⎣⎦，()()22T x t y t =⎡⎤⎣⎦，则()()()()11221122T c x t c x t c y t c y t +=+⎡⎤⎣⎦（1c ，2c 为常数）。