当前位置：文档之家 › 盈亏平衡分析和决策树计算题

盈亏平衡分析和决策树计算题

  • 格式：doc
  • 大小：81.50 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

决策树练习题计算题

决策树练习题计算题

决策树练习题计算题计算题1.为⽣产甲产品，⼩⾏星公司设计了两个基本⽅案：⼀是建⼤⼯⼚，⼆是建⼩⼯⼚。

如果销路好，3年以后考虑扩建。

建⼤⼯⼚需投资300万元，建⼩⼯⼚需投资160万元，3年后扩建另需投资140万元。

扩建后可使⽤7年，其年度损益值与⼤⼯⼚相同。

每种⾃然状态的预测概率及年度损益值如下表：前 3 年后 7 年根据上述资料试⽤决策树法做出决策。

2、计算题（15分）答：建⼤⼚收益=581-300=281建⼩⼚收益=447-160=287所以应选择建⼩⼚⽅案。

3.⼭姆公司的⽣产设备已经落后，需要马上更新。

公司有⼈认为，⽬前产品销路增长，应在更新设备的同时扩⼤再⽣产的规模。

但也有⼈认为，市场形势尚难判断，不如先更新设备，3年后再根据形势变化考虑扩⼤再⽣产的规模问题。

这样，该公司就⾯临着两个决策⽅案。

决策分析的有关资料如下：A、现在更新设备，需投资35万元， 3年后扩⼤⽣产规模，另需投资40万元。

B、现在更新设备的同时扩⼤再⽣产的规模，需投资60万元。

C、现在只更新设备，在销售情况良好时，每年可获利6万元；在销售情况不好时，每年可获利4、5万元。

D、如果现在更新与扩产同时进⾏，若销售情况好，前3年每年可获利12万元；后7年每年可获利15万元；若销售情况不好，每年只获利3万元。

E、每种⾃然状态的预测概率如下表前 3 年后 7 年根据上述资料试⽤决策树法做出决策。

答案：结点7收益值=0、85×7 × 15+0、15 ×7 ×3=92、4（万元）结点8收益值=0、85×7 ×6+0、15 ×7 ×4、5=40、4（万元）结点9收益值=0、1×7 × 15+0、9 ×7 ×3=29、4（万元）结点10收益值=0、1×7 × 6+0、9 ×7 ×4、5=32、6（万元）结点1收益值=0、7×[52、4+（3 × 6）]+0、3 ×[32、6+（3 × 4、5）]=63、1（万元）结点2收益值=0、7×[92、4+（3 × 12）]+0、3 ×[29、4+（3 × 3）]=101、4（万元）答：⽤决策树法进⾏决策应选择更新扩产⽅案，可获得收益41、4万元。

企业决策 计算题

企业决策 计算题

• 降低单位变动成本Cv=13.8
• 降低固定成本F=4.8
• 提高价格p=20.2
⒈确定型决策方法——盈亏平衡分析法
运用盈亏分析法，还可通过计算经营安全率分析企业经营安全状态。 经营安全率是反映企业经营状态的一个重要指标，当销售量或销售收 入越大时，企业经营安全率L 就越接近于1，说明企业经营越安全，亏 损风险越小；若越接近于0时，企业亏损风险就越大。 经营安全率高，说明经营状态好；反之，经营安全率低，说明经营状 态差。一般根据下页表中所示来判断经营安全状态。其计算公式为：
M F S3 5 2 5 (1 0 1% 0 1) 5 10(台 1)250
T
0 .5
• 例某工厂车间生产单一产品，车间生产面积为500 ㎡，单位面积有效工作时间为每日12小时，每生 产一件产品占用时间为1小时，每件产品占用生产 面积2.5㎡，该车间的生产能力为多少？
M FB1 2500 24(件 0)0 bT 2.5 1
方案、状态数据表 单位:万元
（1）画决策树图
47万
（2）计算损益期望值
E 1 0 .6 5 0 0 .3 2 0 5 .1 ( 2 ) 5 3 万 5 元
E 2 0 .6 7 0 0 .3 3 0 0 .1 ( 4 ) 0 4 万 7 元
显然“最大收益”中最大值为70万元，其对应的方案是 “新建方案”。这种选择方案的思路是从最好的情况下寻找最 有优的方案，实际上偏于乐观。
Ⅱ定量决策方法
⒉不确定型决策方法
• ②悲观准则： 小中取大法，找出每个方案在各种自然状态下最小损益值，取 其中大者所对应的方案即为合理方案。
例3：设某企业为了增加产量而设想了三种方案，一是扩 建现有工厂，二是新建一个分厂，三是把增产部分转包给其他 工厂生产，已知未来一段时期市场对产品的要求状态有好、 中、差三种状态。而各种方案在每种状态下的预计损益值，如 下页表所示，试问如何决策？

管理学计算题练习汇总

管理学计算题练习汇总

管理学原理计算题胡世明计算题训练——一.确定型决策（盈亏平衡分析（量本利分析））（一）明辉度假村营业旺季为12周，接待能力共150套客房，每套收费1200元/周，单位变动成本800元/周，固定成本480000元/年。

求：（1）明辉度假村盈亏平衡点；（2）若实际接待是总能力的80%，求明辉度假村旺季营业的总利润；（3）旺季过后，收费降至每套1000元/周，预期可预定总能力75%，问明辉度假村是否继续营业？【参考答案】（1）盈亏平衡点Q* = FC / ( P - A VC ) =（480000÷12/）（1200 - 800）=100（套）（2）总利润∏= ( P - A VC )×Q - FC =（1200 - 800）×150×12×80% - 480000 =96000（元）（3）因为1000元/周>800元/周，即服务或产品单价高于单位变动成本，短期内企业可以继续营业。

（二）某企业经销一种产品，产品的单位变动费用（A VC）50元，售价（P）100元，每年固定费用（FC）90万元。

依此，试解析——1．此企业盈亏平衡点的产量（Q*）为多少？2．如果企业现有生产能力为2．4万件，问每年能获得利润（Π）多少？3．为满足市场对产品需要，扩大生产，拟购置一条生产线，每年增加固定费用20万元，但可节约变动费用10元/件，与此同时，为了扩大产品销售计划，拟降低售价10%，在现有生产能力条件下，较之原方案，此方案是否可行？若不可行，而要获取不低于原方案的利润，在什么情况下此方案可行？【参考答案】1．求盈亏平衡点产量Q* = FC/ (P - A VC) = 900000 / (100 - 50) = 18000 (件)2．企业现有能力2.4万件，每年可获得的利润∏= ( P - A VC ) ×Q –FC= (100 - 50)×24000 – 90000 = 300000(元)3．购置一条生产线方案的可行性FC购置= 90 + 20 = 110 (万元)；A VC 新= 50 – 10 = 40 (元/件)； P = 100 (1 - 10%) = 90 (元/件)；利润∏= ( P - A VC ) ×Q - FC = ( 90 – 40 ) ×24000 – 1100000 = 100000（元）；100000（元）＜300000(元)，利润低于原方案，在现有生产能力下，如果不扩大生产，新方案实施后利润下降了20万元，此方案不可行。

决策树练习题计算题

决策树练习题计算题
悲观决策法指当存在几种自然状态的情况下，宁可把情况估计得坏一
些，从中选择一个收益最大的方案，决策稳妥可靠。按此准则，在低需求的自然状态下，5年内新建方案亏损160万，扩建方案保本，改造方案获利80万。改造方案最佳。
乐观决策法：
新建E=（0、7X600）+（1-0、7）X（-160）=372（万元）
扩建E=（0、7X400）+（1-0、7）X0=280（万元）
请分别用悲观决策法、乐观决策法（设定乐观系数为0、6）和最大最小后悔决策法进行决策。
答案
悲观决策法指当存在几种自然状态的情况下，宁可把情况估计得坏一些，从中选择一个收益最大的方案，决策稳妥可靠。按此准则，应选择方案（3）
乐观决策法：
（1）0、6X800，000+0、4X（-700，000）=200，000
（2）0、6X550，000
（3）0、6X310，000+0、4X（-10，000）=182，000
最大最小后悔决策法：根据计算乐观决策的结果应选择方案（2）
五
某公司为满足某地区对某一产品的需求设计了三个方案：第一个方案是新建一个大工厂,需投资320万元；第二个方案是新建一个小工厂,需投资140万元；第三方案是先投资140万元建造一个小工厂,三年以后,如果销路好再考虑扩建，扩建需追加投资200万元,收益与新建大工厂方案相同。根据预测该产品在前三年销路好的概率为0.7，销路差的概率为0.3。如果前三年销路好,后七年销路好的概率为0.9,销路差的概率为0.1;如果前三年的铺路差,则后七年的销路必定差。每个方案的收益如下表所示。
E、每种自然状态的预测概率如下表
前3年
后7年
答案：根据上述资料试用决策树法做出决策。
结点7收益值=0、85×7 × 15+0、15 ×7 ×3=92、4（万元）

管理学盈亏平衡分析和决策树计算题

管理学盈亏平衡分析和决策树计算题

盈亏平衡分析某建筑工地需抽除积水保证施工顺利进行，现有A 、B 两个方案可供选择。

A 方案：新建一条动力线，需购置一台电动机并线运转，其投资为1400元，第四年末残值为200元，电动机每小时运行成本为元，每年预计的维护费用120元，因设备完全自动化无需专人看管。

B 方案：购置一台的（5马力）柴油机，其购置费用为550元，使用寿命为4年，设备无残值。

运行每小时燃料费为元，平均每小时维护费为元，每小时的人工成本为元。

若寿命都为4年，基准折现率为10％，试比较A 、B 方案的优劣。

解：两方案的总费用都与年开机小时数t 有关，故两方案的年成本均可表示t 的函数。

)4%,10,/(200)4%,10,/(1400F A P A C A -=t t 84.056.51884.0120+=++t P A C B )8.015.042.0()4%,10,/(550+++=t 37.151.175+=令C A =C B ，即+=+可解出：t =651(h),所以在t =651h 这一点上，C A =C B =（元）A 、B 两方案的年成本函数如图13所示。

从图中可见，当年开机小时数低于651h ，选B 方案有利；当年开机小时数高于651h 则选A 方案有利。

决策树问题 55.某建筑公司拟建一预制构件厂，一个方案是建大厂，需投资300万元，建成后如销路好每年可获利100万元，如销路差，每年要亏损20万元，该方案的使用期均为10年；另一个方案是建小厂，需投资170万元，建成后如销路好，每年可获利40万元，如销路差每年可获利30万元；若建小厂，则考虑在销路好的情况下三年以后再扩建，扩建投资130万元，可使用七年，每年盈利85万元。

假设前3年销路好的概率是，销路差的概率是，后7年的销路情况完全取决于前3年；试用决策树法选择方案。

决策树图示考虑资金的时间价值，各点益损期望值计算如下：点①：净收益＝[100×(P/A，10％，10)×+(-20)×（P/A，10％，10）×]-300=(万元)点③：净收益＝85×(P/A，10％，7)×=(万元)点④：净收益＝40×(P/A，10％，7)×=(万元)可知决策点Ⅱ的决策结果为扩建，决策点Ⅱ的期望值为+＝（万元）点②:净收益＝（+）×+40×(P/A，10％，3)×+30×(P/A，10％，10)×＝（万元）由上可知，最合理的方案是先建小厂，如果销路好，再进行扩建。

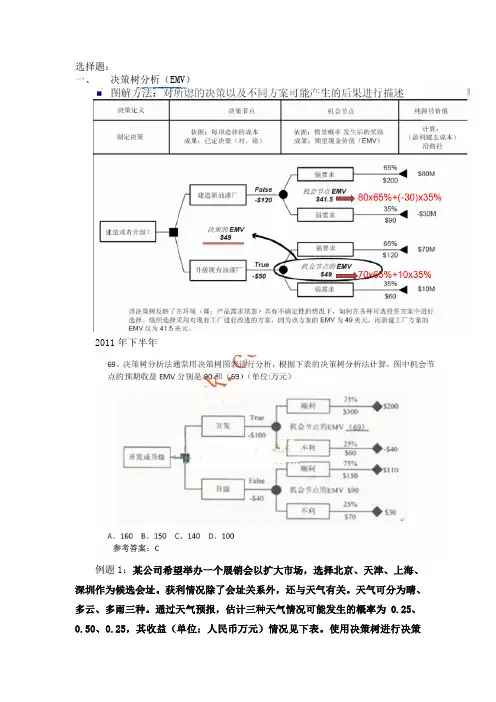
软考中项、高项常见计算题详解

软考中项、高项常见计算题详解

选择题：一、决策树分析（EMV）2011年下半年例题1：某公司希望举办一个展销会以扩大市场，选择北京、天津、上海、深圳作为候选会址。

获利情况除了会址关系外，还与天气有关。

天气可分为晴、多云、多雨三种。

通过天气预报，估计三种天气情况可能发生的概率为0.25、0.50、0.25，其收益（单位：人民币万元）情况见下表。

使用决策树进行决策的结果为（61）。

（61）A．北京B．天津C．上海D．深圳答案：B解析：北京的期望货币值为 4.5×0.25+4.4×0.5+1×0.25＝3.575 天津 5×0.25+4×0.5+1.6×0.25＝3.65上海 6×0.25+3×0.5+1.3×0.25＝3.325深圳 5.5×0.25+3.9×0.5+0.9×0.25＝3.55例题2 （2008上）某电子商务公司要从A地向B地的用户发送一批价值90000元的货物。

从A地到B地有水、陆两条路线。

走陆路时比较安全，其运输成本为10000元；走水路时一般情况下的运输成本只要7000元，不过一旦遇到暴风雨天气，则会造成相当于这批货物总价值的10%的损失。

根据历年情况，这期间出现暴风雨天气的概率为1/4，那么该电子商务公司_(70)。

A．应选择走水路B．应选择走陆路C．难以选择路线D．可以随机选择路线答案： A。

陆路10000水路7000×3/4+（7000+90000×10%）×1/4＝9250例题3二、盈亏平衡点盈亏平衡点（Break Even Point,简称BEP）又称零利润点、保本点、盈亏临界点、损益分歧点、收益转折点。

通常是指全部销售收入等于全部成本时（销售收入线与总成本线的交点）的产量。

以盈亏平衡点的界限，当销售收入高于盈亏平衡点时企业盈利，反之，企业就亏损。

盈亏平衡点可以用销售量来表示，即亏平衡点的销售量；也可以用销售额来表示，即盈亏平衡点的销售额。

利用期望值、决策树等解管理学计算题示范

利用期望值、决策树等解管理学计算题示范
要注意事件 5，有两个工序 E 和 F 都通向事件 5，也就是说，如果按照前面的方法，事件 5 的最早开始时间就有两个了，
一个是 （事件 3 的最早开始时间+工序 E 的作业时间）=17 一个是 （事件 4 的最早开始时间+工序 F 的作业时间）=12 记住一点：计算某事件的最早开始时间时，如果有多个工序通向这个事件，那么就选择由 这些工序分别计算的最早开始时间中最大的那个。 那么，事件 5 的最早开始时间是 （事件 3 的最早开始时间+工序 E 的作业时间）=17 根据上面的思路，可以得出：事件 8 的最早开始时间是 32
第四步：计算每个时间的最晚开始时间，标注在各个事件旁的
中
注意，计算最晚开始时间，要从右向左计算，即从终点事件开始算
还要注意，最后要根据
--
=0 来判断关键路线，关键路线里，肯定包括始点
事件和终点事件，也就是说，始点时间的最早开始时间和最晚开始事件都是 0，而终点事
件的最晚开始时间只要根据第三步里面计算的最早开始时间就可推得。
一个是 （事件 5 的最早开始时间-工序 F 的作业时间）=11 一个是 （事件 4 的最早开始时间-工序 G 的作业时间）=18 记住一点：计算某事件的最晚开始时间时，如果有多个工序从这个事件引出，那么就选择 由这些工序分别计算的最晚开始时间中最小的那个。 那么，事件 4 的最晚开始时间是 （事件 5 的最晚开始时间-工序 F 的作业时间）=11 根据上面的思路，可以得出：事件 3 的最晚开始时间是 12， 事件 2 的最晚开始时间是 4
2
C
D
6
I
3
E
H
5
8
F
4
G
J
7
第三步：计算每个事件的最早开始时间，标注在各个事件旁的

决策练习题

决策练习题

第三，扩大商品销售量，设增加的销售量为Q1 ，则： Q1 = （5000+38500）/〔（20 × 95%）-15〕=10875（件） 如果其他条件不变，销售量由10000件增加到10875件， 可实现目标利润。 第四，提高商品价格，设提高商品售价为P1 ，则： P1=（5000+15 × 10000+38500）/10000 ×95%=20.37(元) 如果其他条件不变，价格由20元提高到20.37元，可实现目 标利润。
5.某企业为了扩大产品的生产，拟建新厂。根据市场预测， 产品销路好的概率为0.8，销路差的概率为0.2。有两种方案 可供企业选择。 方案一 新建大厂，需要投资100万元，销路好时，每年可获 利80万元；销路差时，每年可获利20万元。服务期为4年。 方案二 新建小厂，需要投资30万元，销路好时，每年可获 利50万元；销路差时，每年可获利10万元。服务期也为4年。 试求：应用决策树选择方案。
比较各方案的期望收益值，选择大批量方案， 剪去中批量和小批量方案枝。
2.某厂为生产某种产品设计了三个方案。 2.某厂为生产某种产品设计了三个方案。 某厂为生产某种产品设计了三个方案 方案1 新建一个大车间，需要投资300万元。 方案1：新建一个大车间，需要投资300万元。 300万元 方案2 新建一个小车间，需要投资160万元。 方案2：新建一个小车间，需要投资160万元。这两种车间 160万元 的使用年限都是10 10年 根据市场调查的资料预测， 的使用年限都是10年。根据市场调查的资料预测，前三年销 路好的概率为0.7 如果前三年销路好，则后7 0.7； 路好的概率为0.7；如果前三年销路好，则后7年销路好的概 率可提高到0.9；如果前三年销路差，则后7年销路肯定差。 率可提高到0.9；如果前三年销路差，则后7年销路肯定差。 0.9 方案：先建一个小车间，如果销路好，则三年后再扩建， 方案：先建一个小车间，如果销路好，则三年后再扩建， 其扩建投资需要140万元，假定扩建后可使用7年。问应该如 其扩建投资需要140万元，假定扩建后可使用7 140万元 何决策？ 何决策？三个方案的年度收益值表如下表所示 自然状态 销路好 销路差 投资 概率 0.7 0.3 方案1 方案2 方案1 方案2 100 -20 300 40 10 160 方案3 方案3 前3年 后7年 40 100 10 -20 160 140

多产品下,盈亏平衡点的计算例题

多产品下,盈亏平衡点的计算例题

多产品下，盈亏平衡点的计算例题
假设某公司生产两种产品A和B，每种产品的固定成本分别为20,000元和15,000元，变动成本分别为5,000元和3,000元。

产品A的销售价格为10元/件，产品B的销售价格为8元/件。

1. 计算产品A的盈亏平衡点。

盈亏平衡点的计算公式为：盈亏平衡点=固定成本/（销售价格-变动成本）
产品A的盈亏平衡点=固定成本/（销售价格-变动成本）=（20,000元/件+5,000元/件）/（10元/件-5,000元/件）=4000件。

因此，产品A的盈亏平衡点为4000件。

2. 计算产品B的盈亏平衡点。

盈亏平衡点的计算公式为：盈亏平衡点=固定成本/（销售价格-变动成本）
产品B的盈亏平衡点=固定成本/（销售价格-变动成本）=（15,000元/件+3,000元/件）/（8元/件-3,000元/件）=3000件。

因此，产品B的盈亏平衡点为3000件。

3. 计算两种产品的盈亏平衡点。

两种产品的盈亏平衡点=固定成本/（销售价格-变动成本）
=（20,000元/件+15,000元/件+5,000元/件+3,000元/件）/（10元/件-5,000元/件）=1000件。

因此，两种产品的盈亏平衡点为1000件。

综上所述，该公司至少需要销售1000件产品才能达到盈亏平衡点，即总收入等于总成本，既没有盈利也没有亏损。

如果销售量低于1000件，那么它将会亏损；如果销售量超过1000件，那么它将会盈利。

因此，盈亏平衡分析可以帮助企业确定最低的生产和销售水平，以避免亏损。

风险决策和盈亏分析计算题最全题库

风险决策和盈亏分析计算题最全题库

Ｅ（全套）＝（120×0.3＋70×0.5＋20×0.2）
×8－200＝400 Ｅ（部分）＝（90×0.3＋65×0.5＋45×0.2）
×8－140＝408
12
2
课堂练习2
• 设某厂进行生产能力决策。根据市场预测可 能有好、中、差三种自然状态，市场形势好 时，年销售量可达10万件；市场形势中等时， 年销售量8万件；市场形势差时，只能年销 售5万件。其概率分别为0.3，0.5，0.2。与 之对应的生产能力有年产10万件、8万件、5 万件三种方案，对应的单件成本分别为6元、 7元、8元，产品的最终售价为10元/件。当 然，未卖出去的产品就得报废而损失掉，其
状态结点V8的期望效益值为 EV8＝(-300)×0.1+50×0.5+250×0.4＝95 （万元）。
由于EV8>EV7，所以，剪掉状态结点V7对 应的方案分枝，并将EV8的数据填入决策点 V4，即令EV4＝EV8＝95（万元）。
②状态结点V3的期望效益值为
EV3＝(-100)×0.1+0×0.5+100×0.4＝30 （万元）。
风险型决策的条件
（1）存在着决策者希望达到的目标（如收益最大或 损失最小）； （2）存在着两个或两个以上的方案可供选择； （3）存在着两个或两个以上不以决策者主观意志为 转移的自然状态（如不同的天气对市场的影响）； （4）可以计算出不同方案在不同自然状态下的损益 值； （5）在可能出现的不同自然状态中，决策者不能肯 定未来将出现哪种状态，但能确定每种状态出现的概 率。
2017/11/10
⑤由于EV1>EV2, 所以，剪掉状态结点V2 对应的方案分枝将EV1的数据填入决策点EV， 即令
EV＝EV1＝82（万元）。 综合以上期望效益值计算与剪枝过程可 知，该问题的决策方案应该是：首先采用购 买专利方案进行工艺改造，当购买专利改造 工艺成功后，再采用扩大生产规模（即增加 产量）方案进行生产。

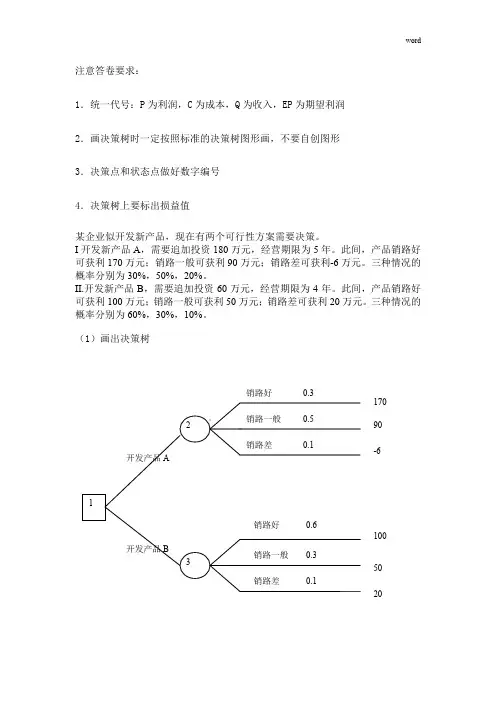
管理学决策树习题及答案

管理学决策树习题及答案

注意答卷要求：1．统一代号：P 为利润，C 为成本，Q 为收入，EP 为期望利润 2．画决策树时一定按照标准的决策树图形画，不要自创图形 3．决策点和状态点做好数字编号 4．决策树上要标出损益值某企业似开发新产品，现在有两个可行性方案需要决策。

I 开发新产品A ，需要追加投资180万元，经营期限为5年。

此间，产品销路好可获利170万元；销路一般可获利90万元；销路差可获利-6万元。

三种情况的概率分别为30%，50%，20%。

II.开发新产品B ，需要追加投资60万元，经营期限为4年。

此间，产品销路好可获利100万元；销路一般可获利50万元；销路差可获利20万元。

三种情况的概率分别为60%，30%，10%。

（1）画出决策树销路好 0.317090 -61005020（2）计算各点的期望值，并做出最优决策求出各方案的期望值：方案A=170×0.3×5+90×0.5×5+(-6)×0.2×5=770(万元)方案B=100×0.6×4+50×0.3×4+20×0.1×4=308(万元)求出各方案的净收益值：方案A=770-180=590(万元)方案B=308-60=248(万元)因为590大于248大于0所以方案A最优。

某企业为提高其产品在市场上的竞争力，现拟定三种改革方案：（1）公司组织技术人员逐渐改进技术，使用期是10年；（2）购买先进技术，这样前期投入相对较大，使用期是10年；（3）前四年先组织技术人员逐渐改进，四年后再决定是否需要购买先进技术，四年后买入技术相对第一年便宜一些，收益与前四年一样。

预计该种产品前四年畅销的概率为0.7，滞销的概率为0.3。

如果前四年畅销，后六年畅销的概率为0.9；若前四年滞销，后六年滞销的概率为0.1。

相关的收益数据如表所示。

（1）画出决策树（2）计算各点的期望值，并做出最优决策投资收益表单位：万元解（1）画出决策树，R为总决策，R1为二级决策。

管理学盈亏平衡分析和决策树计算题

管理学盈亏平衡分析和决策树计算题

盈亏平衡分析某建筑工地需抽除积水保证施工顺利进行,现有A 、B 两个方案可供选择。

A 方案:新建一条动力线,需购置一台2、5W 电动机并线运转,其投资为1400元,第四年末残值为200元,电动机每小时运行成本为0、84元,每年预计的维护费用120元,因设备完全自动化无需专人瞧管。

B 方案:购置一台3、86KW 的(5马力)柴油机,其购置费用为550元,使用寿命为4年,设备无残值。

运行每小时燃料费为0、42元,平均每小时维护费为0、15元,每小时的人工成本为0、8元。

若寿命都为4年,基准折现率为10％,试比较A 、B 方案的优劣。

解:两方案的总费用都与年开机小时数t 有关,故两方案的年成本均可表示t 的函数。

)4%,10,/(200)4%,10,/(1400F A P A C A -=t t 84.056.51884.0120+=++ t P A C B )8.015.042.0()4%,10,/(550+++=t 37.151.175+=令C A =C B ,即518、56+0、84t=173、51+1、37t可解出:t =651(h),所以在t =651h 这一点上,C A =C B =1065、4(元)A 、B 两方案的年成本函数如图13所示。

从图中可见,当年开机小时数低于651h,选B 方案有利;当年开机小时数高于651h 则选A 方案有利。

图13 A 、B 方案成本函数曲线决策树问题55.某建筑公司拟建一预制构件厂,一个方案就是建大厂,需投资300万元,建成后如销路好每年可获利100万元,如销路差,每年要亏损20万元,该方案的使用期均为10年;另一个方案就是建小厂,需投资170万元,建成后如销路好,每年可获利40万元,如销路差每年可获利30万元;若建小厂,则考虑在销路好的情况下三年以后再扩建,扩建投资130万元,可使用七年,每年盈利85万元。

假设前3年销路好的概率就是0、7,销路差的概率就是0、3,后7年的销路情况完全取决于前3年;试用决策树法选择方案。

管理学盈亏平衡点计算例题

管理学盈亏平衡点计算例题

管理学盈亏平衡点计算例题答：盈亏平衡点是指企业在特定的生产和销售条件下，能够达到收支平衡的产量或销售数量。

在这个点上，企业的总成本等于总收入，不会产生盈利也不会产生亏损。

为了计算盈亏平衡点，我们需要知道企业的固定成本、可变成本和售价。

固定成本是企业在生产和销售一定数量的产品时不变的费用，如租金和固定人员工资。

可变成本是与生产和销售数量成正比的费用，如原材料和直接劳动力成本。

售价是企业出售产品的价格。

假设某家公司的固定成本为10000元，可变成本为10元每个产品，售价为20元每个产品。

我们可以使用以下公式来计算盈亏平衡点：盈亏平衡点 = 固定成本 / (售价 - 可变成本)根据所给的数据，我们可以进行计算：盈亏平衡点 = 10000元 / (20元 - 10元)= 10000元 / 10元= 1000个产品这意味着在销售1000个产品时，该公司将达到盈亏平衡点。

销售数量少于1000个产品将导致亏损，销售数量多于1000个产品将产生盈利。

进一步分析示例，我们可以看到在盈亏平衡点上，企业的总成本和总收入相等。

在销售少于1000个产品时，总成本将超过总收入，这将导致亏损。

而在销售多于1000个产品时，总收入将超过总成本，这将产生盈利。

此外，盈亏平衡点还可以用来评估企业的风险和稳定性。

如果盈亏平衡点相对较低，企业在面临市场不确定性和变动时更容易保持盈亏平衡。

然而，如果盈亏平衡点相对较高，企业在市场波动时更容易出现亏损。

总的来说，盈亏平衡点是管理学中一个重要的概念，用于计算企业达到收支平衡的产量或销售数量。

通过计算盈亏平衡点，企业能够评估其生产和销售策略的可行性，并做出相应的调整，以实现盈利和稳定发展。

决策计算题

决策计算题

后悔值原则

决策者认为，在选定方案并实施后，如果遇到的自然 状态表明采用另外的方案会取得更好的收益，这样决 策者将为此感到后悔。因此，决策者要力求使后悔值 尽量小。 采用后悔值原则时，采取的步骤：
o

o o
算出各方案在自然状态下的后悔值（方案在某自然状态下的 收益值与该自然状态下的最大收益值的差）。 将各方案的最大后悔值取出。 从中取最小值，该值相应的方案为最佳方案。
决策树法

决策树就是从一个基点出发，将各种可能性全 部标注在一个树状的图示上，在此基础上再对 最终的决策方案作出选择。
风险型决策 —— 决策树法
• 构成（三点两枝）：
决策点：
状态点： 结果点：
代表最后的方案选择
代表方案将会遇到的不同状态 代表每一种状态所得到的结果
方案枝：由决策点引出的线段，连接决策点和状态点，每 一线段代表一个方案。 概率枝：由状态点引出的线段，连接状态点和结果点。每 一线段代表一种状态。
40
悲观原则

决策者比较悲观，认为不论采取何种方案均可能取得该 方案的最小收益值。 采用悲观原则时，采取的步骤：
o o o
找出各方案在各种自然状态下的最小收益值。 在最小收益值中找最大值。 对收益值进行比较，找出在最差自然状态下能够带来“最大收 益”的方案作为决策实施方案。

悲观决策原则也叫“最小最大收益值规则”。
0 35 80
10 0
30
40 10 0
课后作业：



各组搜集一个企业的决策案例 比如：汽车行业：长城皮卡、吉利汽车等 饮料行业：娃娃哈、王老吉、可口可乐等 服装行业：休闲、运动等、 …… 1、要求：总结归纳其决策成功的要点 2、汇报时间：5分钟 3、详细资料电子版

管理学决策计算题

管理学决策计算题

管理学决策的方法一.确定型决策方法确定型决策是指决策面对的问题的相关因素是确定的，从而建立的决策模型中的各种参数是确定的。

例如：1.某企业可以生产A、B两种产品。

生产单位产品A和B所需要的机器、人工、原材料的数量，每天可用资源的总量和各种资源的价格，都在表中给出。

已知产品A的售价600元，B的售价400元。

市场需求旺盛。

问：如何安排生产能使企业的利润最大？设A为产品A每天的产量B为产品B每天的产量C1为每天使用机器的数量C2为每天使用工人的数量C3为每天使用原材料的数量模型：MAX： 600A+400B-5C1-20C2-1C3 (1)ST： 6A+8B=C1 (2)10A+5B=C2 (3)11A+8B=C3 (4)C1小于等于1200 (5)C2小于等于1000 (6)C3小于等于1300 (7)A大于等于0 (8)B大于等于0 (9)解：(2) (3)连立，得60A+80-60A-30B=10C1-6C250B=10C1-6C2(3) (4)连立，得80A+40B-55A-40B=8C2-5C325A=8C2-5C3MAX： 600A+400B-5C1-20C2-1C1=75C1+124C2-121C3又由 25B=5C1-3C225A=8C2-5C3因为 A20, B20所以 5c1N3C28c2N5C3C3W1300 要使 MAX 最大，则 取 C1=1200, C3=0 ,所以 MAX=75*1200+124*1000-0=214000 即最大利润 为 214000 元二.不确定型决策方法如果决策问题设计的条件中有些是未知的，对一些随机变量，连它们 的概率分布也不知道，这类决策问题被称为不确定型决策。

2 .某企业打算生产某产品。

根据市场预测分析，产品销路有三种可能性：销路 好、一般和差。

生产该产品有三种方案：改进生产线、新建生产线、外包生 产。

各种方案的收益值表在下表给出。

解：1、小中取大法 分别是-40，-80，16第三种方案值最大，选外包生产方案 2、大中取大法分别为180，240，100第二种方案值最大，选新建生产线MAX=75C1+124C2-121C3 又 C1W1200 C2W1000C2=1000,3、最小最大后悔值法:决策者在选择了某方案后，若事后发现客观情况并没有按自己的预想发生，会为自己的决策后悔。

软考中项、高项常见计算题详解

软考中项、高项常见计算题详解

选择题：一、决策树分析（EMV）2011年下半年例题1：某公司希望举办一个展销会以扩大市场，选择北京、天津、上海、深圳作为候选会址。

获利情况除了会址关系外，还与天气有关。

天气可分为晴、多云、多雨三种。

通过天气预报，估计三种天气情况可能发生的概率为0.25、0.50、0.25，其收益（单位：人民币万元）情况见下表。

使用决策树进行决策的结果为（61）。

（61）A．北京B．天津C．上海D．深圳答案：B解析：北京的期望货币值为 4.5×0.25+4.4×0.5+1×0.25＝3.575 天津 5×0.25+4×0.5+1.6×0.25＝3.65上海 6×0.25+3×0.5+1.3×0.25＝3.325深圳 5.5×0.25+3.9×0.5+0.9×0.25＝3.55例题2 （2008上）某电子商务公司要从A地向B地的用户发送一批价值90000元的货物。

从A地到B地有水、陆两条路线。

走陆路时比较安全，其运输成本为10000元；走水路时一般情况下的运输成本只要7000元，不过一旦遇到暴风雨天气，则会造成相当于这批货物总价值的10%的损失。

根据历年情况，这期间出现暴风雨天气的概率为1/4，那么该电子商务公司_(70)。

A．应选择走水路B．应选择走陆路C．难以选择路线D．可以随机选择路线答案： A。

陆路10000水路7000×3/4+（7000+90000×10%）×1/4＝9250例题3二、盈亏平衡点盈亏平衡点（Break Even Point,简称BEP）又称零利润点、保本点、盈亏临界点、损益分歧点、收益转折点。

通常是指全部销售收入等于全部成本时（销售收入线与总成本线的交点）的产量。

以盈亏平衡点的界限，当销售收入高于盈亏平衡点时企业盈利，反之，企业就亏损。

盈亏平衡点可以用销售量来表示，即亏平衡点的销售量；也可以用销售额来表示，即盈亏平衡点的销售额。

最新管理学盈亏平衡分析和决策树计算题资料

最新管理学盈亏平衡分析和决策树计算题资料

盈亏平衡分析某建筑工地需抽除积水保证施工顺利进行，现有A 、B 两个方案可供选择。

A 方案：新建一条动力线，需购置一台2.5W 电动机并线运转，其投资为1400元，第四年末残值为200元，电动机每小时运行成本为0.84元，每年预计的维护费用120元，因设备完全自动化无需专人看管。

B 方案：购置一台3.86KW 的（5马力）柴油机，其购置费用为550元，使用寿命为4年，设备无残值。

运行每小时燃料费为0.42元，平均每小时维护费为0.15元，每小时的人工成本为0.8元。

若寿命都为4年，基准折现率为10％，试比较A 、B 方案的优劣。

解：两方案的总费用都与年开机小时数t 有关，故两方案的年成本均可表示t 的函数。

)4%,10,/(200)4%,10,/(1400F A P A C A -=t t 84.056.51884.0120+=++ t P A C B )8.015.042.0()4%,10,/(550+++=t 37.151.175+=令C A =C B ，即518.56+0.84t=173.51+1.37t 可解出：t =651(h),所以在t =651h 这一点上，C A =C B =1065.4（元）A 、B 两方案的年成本函数如图13所示。

从图中可见，当年开机小时数低于651h ，选B 方案有利；当年开机小时数高于651h 则选A 方案有利。

决策树问题55.某建筑公司拟建一预制构件厂，一个方案是建大厂，需投资300万元，建成后如销路好每年可获利100万元，如销路差，每年要亏损20万元，该方案的使用期均为10年；另一个方案是建小厂，需投资170万元，建成后如销路好，每年可获利40万元，如销路差每年可获利30万元；若建小厂，则考虑在销路好的情况下三年以后再扩建，扩建投资130万元，可使用七年，每年盈利85万元。

假设前3年销路好的概率是0.7，销路差的概率是0.3，后7年的销路情况完全取决于前3年；试用决策树法选择方案。

管理学盈亏平衡分析和决策树计算题教学提纲

管理学盈亏平衡分析和决策树计算题教学提纲

盈亏平衡分析某建筑工地需抽除积水保证施工顺利进行，现有A 、B 两个方案可供选择。

A 方案：新建一条动力线，需购置一台2.5W 电动机并线运转，其投资为1400元，第四年末残值为200元，电动机每小时运行成本为0.84元，每年预计的维护费用120元，因设备完全自动化无需专人看管。

B 方案：购置一台3.86KW 的（5马力）柴油机，其购置费用为550元，使用寿命为4年，设备无残值。

运行每小时燃料费为0.42元，平均每小时维护费为0.15元，每小时的人工成本为0.8元。

若寿命都为4年，基准折现率为10％，试比较A 、B 方案的优劣。

解：两方案的总费用都与年开机小时数t 有关，故两方案的年成本均可表示t 的函数。

)4%,10,/(200)4%,10,/(1400F A P A C A -=t t 84.056.51884.0120+=++ t P A C B )8.015.042.0()4%,10,/(550+++=t 37.151.175+=令C A =C B ，即518.56+0.84t=173.51+1.37t 可解出：t =651(h),所以在t =651h 这一点上，C A =C B =1065.4（元）A 、B 两方案的年成本函数如图13所示。

从图中可见，当年开机小时数低于651h ，选B 方案有利；当年开机小时数高于651h 则选A 方案有利。

图13 A 、B 方案成本函数曲线决策树问题55.某建筑公司拟建一预制构件厂，一个方案是建大厂，需投资300万元，建成后如销路好每年可获利100万元，如销路差，每年要亏损20万元，该方案的使用期均为10年；另一个方案是建小厂，需投资170万元，建成后如销路好，每年可获利40万元，如销路差每年可获利30万元；若建小厂，则考虑在销路好的情况下三年以后再扩建，扩建投资130万元，可使用七年，每年盈利85万元。

假设前3年销路好的概率是0.7，销路差的概率是0.3，后7年的销路情况完全取决于前3年；试用决策树法选择方案。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

公司拟建一预制构件厂，一个方案是建大厂，需投资300万元，建成后如销路好每年可获利100万元，如销路差，每年要亏损20万元，该方案的使用期均为10年；另一个方案是建小厂，需投资170万元，建成后如销路好，每年可获利40万元，如销路差每年可获利30万元；若建小厂，则考虑在销路好的情况下三年以后再扩建，扩建投资130万元，可使用七年，每年盈利85万元。

假设前3年销路好的概率是0.7，销路差的概率是0.3，后7年的销路情况完全取决于前3年；试用决策树法选择方案。

解：这个问题可以分前3年和后7年两期考虑，属于多级决策类型，如图所示。

决策树图示
考虑资金的时间价值，各点益损期望值计算如下：
点①：净收益＝[100×(P/A，10％，10)×0.7+(-20)×（P/A，10％，10）×0.3]-300=93.35(万元)
点③：净收益＝85×(P/A，10％，7)×1.0-130=283.84(万元)
点④：净收益＝40×(P/A，10％，7)×1.0=194.74(万元)
可知决策点Ⅱ的决策结果为扩建，决策点Ⅱ的期望值为283.84+194.74＝478.58（万元）
点②:净收益＝（283.84+194.74）×0.7+40×(P/A，10％，3)×0.7+30×(P/A，10％，10)×0.3-170＝345.62（万元）由上可知，最合理的方案是先建小厂，如果销路好，再进行扩建。

在本例中，有两个决策点Ⅰ和Ⅱ，在多级决策中，期望值计算先从最小的分枝决策开始，逐级决定取舍到决策能选定为止。

为了适应市场的变化，投资者又提出了第三个方案，即先小规模投资160万元，生产3年后，如果销路差，则不再投资，继续生产7年；如果销路好，则再作决策是否再投资140万元扩建至大规模（总投资300万元），生产7年。

前3年和后7年销售状态的概率见表16，大小规模投资的年损益值同习题58。

试用决策树法选择最优方案。

表16 销售概率表
解：（1
（2计算各节点的期望收益值，并选择方案
节点④：[100×7×0.9+(-20) ×7×0.1]=616(万元)
节点⑤：[100×7×0+(-20) ×7×1.0]=-140(万元)
节点②：（616+100×3）×0.7+[(-140)+ (-20)×3]×0.3-300=281.20(万元)
节点⑧：[100×7×0.9+(-20) ×7×0.1]-140=476(万元)
节点⑨：（60×7×0.9+20×7×0.1）＝392（万元）
节点⑧的期望收益值为476万元，大于节点⑨的期望损失值392万元，故选择扩建方案，“剪去”不扩建方案。

因此，节点⑥的期望损益值取扩建方案的期望损益值476万元。

节点⑦：（60×7×0+20×7×1.0）＝140（万元）
节点③：[(476+60×3)×0.7+(140)+20×0.3]-160=359.20(万元)
节点③的期望损益值359.20万元，大于节点②的期望损益值281.20万元，故“剪去”大规模投资方案。

综上所述，投资者应该先进行小规模投资，3年后如果销售状态好则在扩建，否则不扩建。